基于二重网格的动网格松弛法改进
廖佳文, 张力天, 周 璇, 李水乡*
(1.北京大学 工学院,北京 100871; 2.北京应用物理与计算数学研究所,北京 100094)
1 引 言
在流固耦合和多介质流体[1]等实际工程问题中经常需要处理边界移动问题,此时需要根据边界的运动或变形来改变计算网格[2]。网格重构是解决此类问题的一种思路,但计算代价较大[3]。另一种经常采用的处理方法是动网格法[4]。在动网格方法中,计算网格随着边界移动发生变形以适应新的边界[5]。常见的动网格方法[6]有弹簧近似法[7]、径向基函数插值法[8]、距离函数插值法、偏微分方程法和弹性体法等。
从颗粒填充领域的松弛算法受到启发,周璇等[9]提出了一种新颖的基于球松弛算法的动网格方法,称之为动网格松弛法。与弹簧法等虚拟结构类网格变形方法相比,动网格松弛法的网格变形效率更高,网格质量更好。然而,动网格松弛法与径向基函数插值法等代数插值类方法相比,在大规模网格变形中计算效率偏低。
已有的研究表明,采用多套不同节点数网格的多重网格策略能够有效地提高动网格方法的求解效率,是动网格方法改进的一种重要手段。胡会朋等[10]提出了基于背景网格簇和Delaunay图映射的动网格生成方法,该方法变形能力高于弹簧法,且能够直接推广到三维。孙岩等[11]提出了基于径向基函数与混合背景网格的动网格方法,可有效减少径向基函数基点数,有助于提高径向基函数插值的效率。
本文在原有动网格松弛法的基础上,提出了一种基于二重网格的动网格松弛法改进方法。
2 基于二重网格的动网格松弛法改进
本文引入二重网格策略改进了动网格松弛法。通过二重网格映射,将边界位移传递到整个网格计算域,达到减少动网格松弛法迭代次数的目的,从而有效地提高了计算效率。改进后的动网格松弛法包含二重网格映射、球松弛和后优化三个步骤。
2.1 二重网格映射
在原有的非结构计算网格之外,重新在计算区域内生成一套更加稀疏的非结构网格,即粗网格。原有的计算网格称之为细网格。粗细两套网格形成二重网格。
利用面积法,建立细网格节点与粗网格三角形单元之间的对应关系[12]。
αi=si/s
(i=1,2,3)(1)
式中αi为细网格节点在所属粗网格单元中的面积坐标,si(i=1,2,3)分别为细网格节点与所属粗网格单元的节点连接成的三个三角形的面积,s为该粗网格三角形单元的面积。利用松弛算法进行粗网格变形后,通过映射得到细网格节点的新位置(x,y)为
(i=1,2,3)(2)
式中xi和yi(i=1,2,3)为变形后粗网格单元节点的坐标。
2.2 球松弛算法
在球松弛算法中,利用节点分布构造球分布进行松弛移动,得到新的节点分布,其主要步骤如下。
(1) 构造球分布。将节点位置作为球心,连接该节点的边长平均值的一半作为球半径(目的是最小化球之间的重叠量并尽可能相切),如式(3)。采用此方法对计算域进行布球,将计算网格的节点分布转化为球分布。
(3)
式中rj为节点j处的球半径,m为与节点j相连的节点个数,li j为节点j与节点i相连的边长。
(2) 用球松弛算法调整球的位置,以得到区域内球的均匀分布。如图1所示,球松弛将相交和相离的球尽可能转化为相切,调整后的球心位置计算公式为
Rj i=Rj+(Ri-Rj)[(ri+rj)/di j]
(4)
式中Rj i为球i与附近的球j进行松弛操作得到的新的球心位置,ri和rj分别为球i和球j的半径,di j为球i与球j之间的球心距离。通过建立背景网格[13],将邻接球搜索局部化以减少邻接球搜索时间。球i移动后的球心位置计算式为
(5)
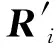

图1 球松弛[9]
在一次迭代中调整每个球的位置,经过多次迭代直到所有球的位移量足够小,则迭代停止,并得到新的节点分布。再利用初始网格的连接关系将这些节点连接起来,得到变形后的网格。
2.3 后优化
为了防止非法网格的出现,本文采用文献[9]的后优化过程。图2给出了后优化过程的二维示例,对于节点j,与其连接的节点形成的网格区域定义为区域D,对于区域D的每条边,向区域内部尝试做等边三角形。等边三角形的另一个顶点位置矢量为Ri j(i=1,2,…,n),n为区域D的边长总数,节点j的新位置Rj由所有的相对位置Ri j决定,
(6)
式中hi j为节点j到区域D边i的垂直距离。后优化过程可以防止非法网格的出现。
图2 后优化算法
3 数值算例与讨论
本文通过二维NACA0012翼型转动、矩形平动和转动以及三维梁弯曲三个典型算例验证改进松弛法在动网格计算中的特性和效率。计算平台为3 GHz主频,16 GB内存的台式机。
3.1 NACA0012翼型转动
平面NACA0012翼型在矩形区域内逆时针转动[9],计算区域的大小为20C×20C,其中C为翼型的弦长。三角形计算网格节点数为29382。将翼型的运动过程分为若干步,每步翼型转动角度为5°。在细网格节点数固定的情况下,选取多组不同疏密程度的粗网格进行对比。粗细网格节点数之比(以下称网格比,在0~1之间)分别取为0.36,0.42,0.46,0.51和0.64。
图3(a)为改进松弛法在翼型旋转110°后的边界局部网格,可以看出,网格变形后的物面边界附近保持了良好的网格质量[14]。图3(b,c)分别为网格变形过程中的最差网格质量和平均网格质量对比。可以看出,改进松弛法的变形能力(极限变形量)与原动网格松弛法相同,但网格质量稍有下降,不同网格比下网格质量差别不大。图3(d)为不同网格比下改进松弛法与原动网格松弛法的计算时间之比。综合在不同网格比下变形后的网格质量和计算时间数据可以发现,随着网格比的增加,变形网格质量是逐步提高的,但计算时间先减小后增大。NACA0012算例显示,当网格比为0.51时,改进松弛法时间效率最优,计算时间减小到原动网格松弛法的50%,同时变形能力保持不变,变形网格质量也基本保持不变。

3.2 矩形平动和转动算例
平面正方形区域边长为500个长度单位,初始时矩形水平置于计算区域中心,矩形的长和宽分别为25和10个单位长度。矩形运动为逆时针旋转同时向正方形区域的左下角平动[15]。三角形计算网格节点数为9012。矩形运动和网格变形分步进行,矩形每步旋转30°并分别向左方和下方各移动 3个单位长度。网格比分别取为0.16,0.25,0.33,0.41,0.45,0.49,0.53,0.65和0.79。
图4(a)为变形21步后的计算网格,图4(b)为改进松弛法与原动网格松弛法的计算时间之比与网格比的关系。从图4(b)可以看出,所有网格比下的计算时间比都小于1,表明基于二重网格的改进松弛法能提高动网格松弛法的计算效率。对不同网格比进行比较,计算时间随着网格比的增大先减小再增大。最优的时间比出现在网格比为0.49处,所用时间为原动网格松弛法计算时间的47.4%。

3.3 三维梁弯曲算例
三维长方体梁尺寸为20×2×0.5单位长度,计算区域是半径为25个单位长度的球[13]。计算网格中有13712个节点,63385个四面体单元。初始时长方形梁水平置于球区域的中心,如图5(a)所示。变形过程中梁向上弯曲,如图5(b)所示。变形过程中梁的中心线圆弧对应的圆心角从0°变化至180°。变形过程分为5步,每步圆心角的变化为36°。
图5(a)为梁附近的局部初始网格,图5(b)为梁弯曲变形第5步后的局部网格(圆心角180°),图5(c)为改进松弛法和原动网格松弛法在不同网格比下的最差网格质量对比,图5(d)给出了改进松弛法与原动网格松弛法的计算时间之比与网格比的关系。可以看出,改进松弛法不但与原动网格松弛法变形能力相同,而且能够有效地提高计算效率。网格比在0.52时计算效率达到最优,这与前面的二维算例所得结论一致。但与二维算例相比,其最优时间比仅为78%。这是因为该三维算例中球松弛迭代的次数远小于二维算例,故二重网格缩减迭代次数的作用减弱,并且三维映射比二维所需计算时间更多。

4 结 论
本文提出了基于二重网格策略的改进动网格松弛法,通过二重网格映射来减少松弛法的迭代次数,从而提高动网格松弛法的计算效率。二维和三维算例的结果表明,(1)改进后的方法在保持网格变形能力和变形网格质量基本不变的前提下,能够有效地提高网格变形的计算效率; (2) 随着粗细网格比的增加,平均网格质量和最差网格质量均单调上升,但计算时间先增大后减小。其原因在于随着网格比的增加,虽然粗网格变形所需的计算时间不断增加,但松弛算法的迭代次数会相应减少,因此叠加起来总的计算时间出现先增大后减小; (3) 粗细网格比在0.5左右时达到最优计算效率。
本文研究表明,采用二重网格策略并选取适当的粗细网格比可以有效地提高动网格松弛算法的计算效率,为该方法在大规模网格计算中的应用提供了有力的支撑。

