联合极限状态下基于最大熵可靠度的易损性分析

何 乡， 吴子燕， 贾大卫

(西北工业大学 力学与土木建筑学院，西安 710129)

1 引 言

地震易损性定义为在不同强度地震激励下，结构超过给定性能极限状态的概率。地震激励具有很强的不确定性，因此在传统的理论地震易损性研究中，基于概率理论的随机模型得到了广泛应用[1，2]。如Wang等[1]将桥梁结构的响应参数视为服从对数正态分布的随机变量，通过极大似然估计法得到对数均值和标准差，建立了在不同强度地震下结构的概率地震需求模型，通过蒙特卡洛模拟(MC)法计算结构的破坏概率。Mosallam等[2]基于概率易损性理论，建立了钢框架结构的易损性函数。在传统地震易损性研究中，首先需要假定地震响应参数服从对数正态分布。但文献[3]表明，这种假设只是一种近似假设，部分参数并不符合这一假定，因此该方法具有一定局限性。

为克服传统计算方法的不足，学者们提出了多种不同的易损性分析模型。如樊剑等[4]提出了一种概率-凸集混合模型用于地震易损性研究；董俊等[5]在不对EDP分布进行人为假定的前提下，通过核密度估计法建立EDP概率密度函数，从而进行桥梁易损性分析。上述文献仅考虑了桥梁构件的易损性，并未涉及多构件联合作用下的易损性分析。Zhang等[6]利用四阶矩可靠性法对桥墩柱在非平稳地震激励下的可靠度进行了研究，但同样没有涉及桥梁的联合极限状态。贾大卫等[7]提出了一种凸集模型用于地震易损性计算，但该方法需要对凸集变量的每个样本点进行MC模拟求解失效概率，其本质为两阶段MC法。MC法通常需要进行数万次数值模拟，计算成本较大，不利于实际应用。

本文基于结构的联合极限状态，提出一种最大熵可靠度法用于易损性分析。该方法通过统计分析确定结构响应参数的高次阶矩，不需要人为假定其分布类型，也不需要通过MC法进行数值模拟求解失效概率，具有较强的通用性。

2 基于最大熵原理的可靠度计算

2.1最大熵原理

假设某随机事件服从离散分布，可能出现的结果数量为n，每个结果出现的概率为pi(i=1,2,…,n)，将事件的不确定程度表示为

(1)

式中c为大于0的常数，H称为Shannon熵。若pi=1，代表该事件仅有一种结果，不具有不确定性，H=0；若pi=1/n，则认为所有可能结果出现的概率相同，表明该事件的不确定性最大，H取最大值clnn。

若随机事件服从概率密度函数为fX(x)的连续分布，Shannon熵表示为

(2)

Shannon熵在事件发生前是对其不确定性的一种度量指标，事件发生后是从该事件所得到的信息的度量。最大熵原理的含义是，在给定的约束条件下使熵达到最大值，得到偏差最小的概率分布。由此可得一种构造最佳概率分布的途径。

将最大熵理论引入可靠度计算后，对基本随机变量的分布不进行任何人为假定，而是从统计资料得到随机变量的各阶矩，利用最大熵原理，得到极限状态方程的概率密度函数，计算失效概率。将随机变量的前m阶原点矩作为约束条件，在式(3)条件下使式(2)取最大值，

(3)

式中vX i为第i阶原点矩(i=0,1,…，m)。式(3)等价于给定随机变量的中心矩,

(4)

式中μX为随机变量的均值。利用Lagrange乘子法，联立式(2,3)，引进修正函数,

(5)

式中λ0,λ1,…,λm为待定系数。在稳定点处有∂L/∂fX(x)=0，即

(6)

取ai=-λi/c(i=0,1,…，m)，可得最大熵概率密度函数为

(7)

2.2 基于高阶中心矩的可靠度计算

由2.1节可知，在基于最大熵原理的可靠性计算中，需要获得基本随机变量X的高阶中心矩建立最大熵概率密度函数。实际工程中通常可通过统计分析得到X的前四阶矩统计参数，即

(8)

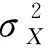
(9)

参数c0，c1，c2和d可用X的前四阶中心矩表示，

(10)

文献[8]表明，各阶中心矩存在如下递推关系,

(11)

随机变量的各阶矩数值差异可能会很大，因此将X转化为标准正态随机变量Y，Y的前四阶矩可以表示为

(12)

在标准空间内，式(10)可写为

(13)

拟定极限状态方程为Z=gX(X)，当基本随机变量的前四阶矩已知时，将极限状态方程在设计点x*处泰勒展开至二次项，估算极限状态方程前四阶中心矩，可表示为

(14)

(15)

(16)

(17)

将极限状态方程标准化为Y=(Z-μZ)/σZ，在标准空间内，将式(7,12)代入式(3)，得到积分方程组,

(18)

从中可以求出系数a0,a1,…，am，则失效概率可以表示为[8]

(19)

由式(14～19)可知，最大熵法采用了极限状态方程的前四阶中心矩作为约束条件，建立最大熵概率密度函数求解失效概率，因此该方法可简称为最大熵二次四阶矩法。

3 基于联合极限状态的易损性分析

在易损性研究中，联合极限状态又称为结构整体性能水准，指将结构构件的性能极限状态与非结构构件的性能极限状态相结合得到的极限状态[9],可用多维性能极限状态方程表示,

(20)

式中Ri为工程需求参数(EDP)，ri lim为阈值，Ni为相互作用因子。当L(R1,…,Rn)>0时认为结构发生破坏。仅考虑两种EDP时，可将一个EDP对应的N取1，式(20)可简化为

L(R1,R2)=(R1/r1 lim)+(R2/r2 lim)N-1

(21)

文献[10]表明，联合极限状态下结构易损性可表示为式(22)所示的积分,

F=∬L > 0f(R1,R2|IM)dR1dR2

(22)

式中IM为给定的地震强度，可采用地面峰值加速度(PGA)表示。f(·)为随机变量的联合概率密度函数。若随机变量相互独立，式(22)写为

F=∬L > 0f(R1|IM)f(R2|IM)dR1dR2

(23)

4 基于最大熵可靠度的易损性分析

由式(23)可知，联合极限状态下地震易损性分析的本质，是在给定地震强度下计算极限状态方程大于0的概率。式(23)所示的积分通常难以计算，Wang等[1]采用蒙特卡洛(MC)模拟法进行求解，刘晓晓等[10]利用数值积分法求解，而这两种方法所需计算成本都很高，不利于实际应用。本文考虑EDP的前四阶矩，提出基于最大熵理论的易损性分析方法，具体步骤如下。

(1) 选择合适的EDP，建立联合性能极限状态方程。

(2) 选择多条地震波，以PGA衡量地震强度，将每条地震波的PGA分别调幅至0.05 g～0.8 g，间隔取0.05 g进行非线性时程分析，获得每条地震波加载下两种EDP的值。

(3) 利用式(8～13)分别在不同PGA下计算EDP的前四阶统计矩和中心矩，然后利用式(14～17)计算极限状态方程的前四阶中心矩，最后利用式(18，19)求解失效概率，得到易损性曲线。

由上述步骤可知，本文所提基于最大熵二次四阶矩的易损性分析法优势在于：

(1) 考虑地震激励的不确定性，从分析结果中获得了EDP的前四阶统计矩，而不需要对EDP的分布类型进行人为假定，使计算结果更具一般性。

(2) 利用最大熵概率密度函数进行失效概率计算，将二重积分简化为一维积分，同时避免了MC模拟，提高了计算效率。

5 算例分析

5.1 结构模型

本文基于SAP2000建立8层RC框架-剪力墙结构模型。每层高均3 m，跨长6 m，X向为5跨，Y向为3跨。各构件采用的混凝土强度等级均为C30，纵向受力钢筋采用HRB335级，箍筋采用HPB300。框架柱截面尺寸为0.6 m×0.6 m，梁截面尺寸为0.25 m×0.5 m。楼板厚度为0.1 m，剪力墙的厚度均为0.2 m，配筋均为双排钢筋，采用HRB335级钢筋。结构模型如图1所示。

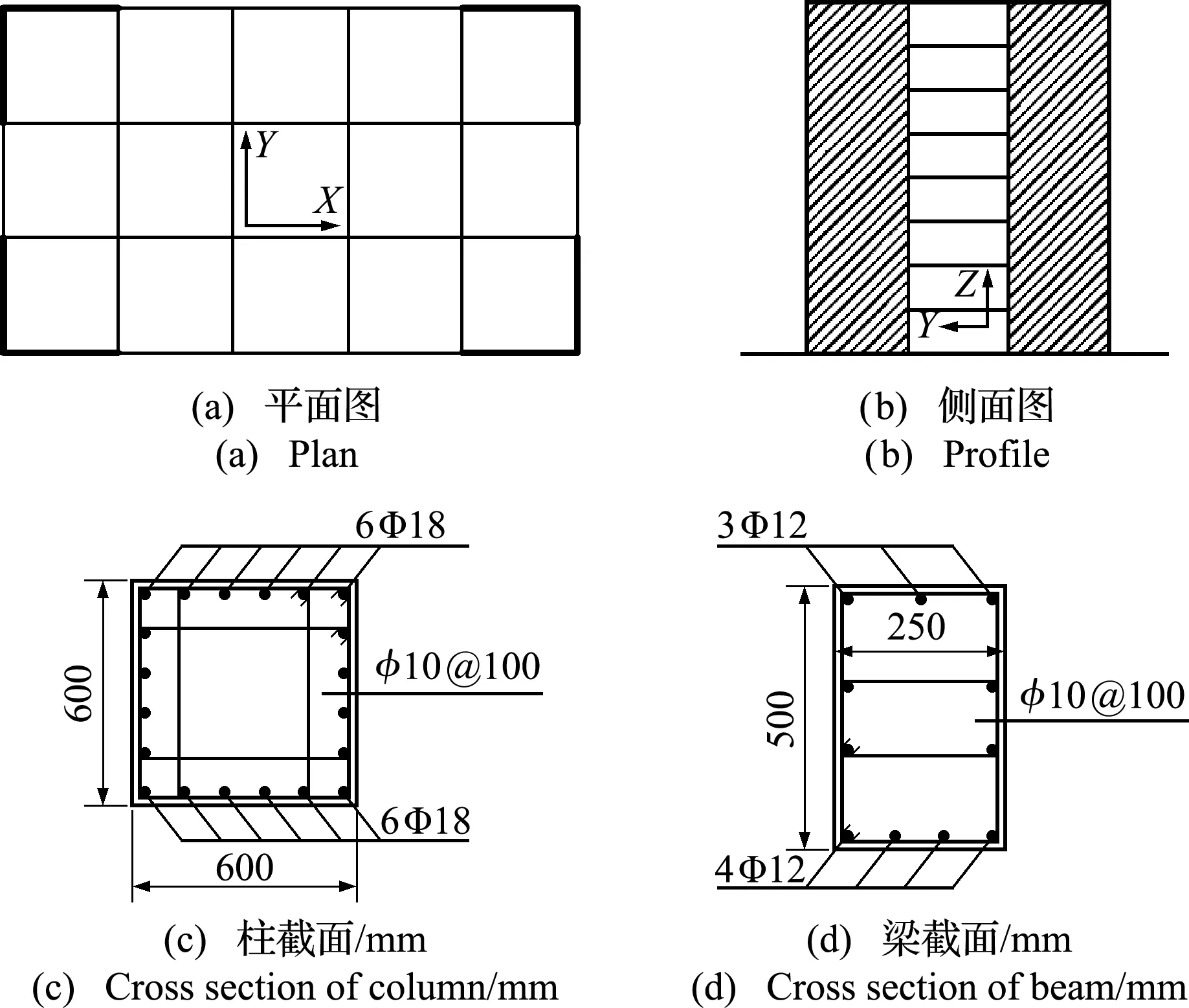
图1 结构模型

混凝土楼板采用SAP2000的膜(Membrane)单元模拟，梁和柱均采用框架单元(Frame)模拟。结构的非线性行为主要体现在梁、柱和剪力墙上。在梁两端设置弯矩铰(M3)，柱两端设置轴力-弯矩铰(P-M2-M3)来模拟非线性行为[11]，剪力墙采用分层壳单元。此外，结构模型考虑了P-Δ效应。本文采用的混凝土和钢筋的本构关系如图2所示。

图2 材料本构关系

本文将框剪结构的联合性能极限状态分为正常使用(NO)、可以使用(IO)、生命安全(LF)和防止倒塌(CP)四级，选择使用最广泛的最大层间位移角(MIDR)作为衡量结构构件性能的EDP。郑山锁等[12]指出，结构整体性能水平达到IO时构件处于开裂状态，MIDR的阈值大致取LF的50%；LF的阈值大致取到规范弹性限值和弹塑性限值的平均值； CP大致取到规范的弹塑性变形限值的90%。基于《建筑抗震设计规范》(GB 50011-2010)[13]对框架-剪力墙类结构阈值的规定，本文采用的MIDR阈值列入表1。

表1 性能极限状态阈值

韩建平等[14]指出，在考虑非结构构件性能时，主要考虑对加速度敏感的构件，如机械设备和内部管道等，因而本文选择最大层加速度(PFA)作为衡量非结构构件损伤大小的EDP。取文献[14]建议的PFA阈值，列入表1。表中g=9.8 m/s2。

5.2 地震波选择

拟定该框架所处的场地土类别为II，设计基本地震动加速度为0.2g，阻尼比取0.05，特征周期为0.35 s，震中距取20 km，利用条件均值反应谱作为目标反应谱[15]，从Pacific Earthquake Enginee -ring Research Center数据库中筛选了60条真实地震波衡量地震激励的不确定性。加速度反应谱如图3所示。

图3 地震波反应谱

5.3易损性分析

本文选择两种EDP衡量联合性能极限状态，基于式(21)建立极限状态方程，可表示为

L=(MIDR/midrlim)+(PFA/pfalim)N-1

(24)

式中midrlim，pfalim分别为MIDR和PFA的阈值。将表1的数值代入式(24)即可得到四种性能极限状态下的极限状态方程。本文首先取未知参数N=2进行易损性计算，后文将通过灵敏度分析探究N对失效概率的影响。暂不考虑两种EDP的相关系数，分别在不同PGA下获得两种EDP的前四阶矩，利用最大熵可靠度理论计算失效概率。表2 给出了部分PGA下NO极限状态方程的前四阶中心矩。为验证本文所提方法的计算结果，同样假定两种EDP均服从对数正态分布，采用MC法计算失效概率，通过累计对数正态分布拟合得到易损性曲线。文献[1]对基于对数正态分布假定的易损性分析进行了详细的研究，本文不再做详细描述，易损性曲线如图4所示。

图4 易损性曲线

可以看出，在四种性能极限状态下，本文方法所得易损性曲线与基于对数正态分布假定的易损性曲线差异很小，曲线基本重叠，在不同PGA下，失效概率最大差值仅为0.04，在易损性分析中这个差异可忽略不计，因此本文所提方法可以得到精度较高的易损性曲线。 还可以看出，对于RC框架类结构，基于对数正态分布假定和高次阶矩的易损性曲线差异很小，PGA变化并不会导致两种分析方法得到的失效概率产生显著差异，因此本文所提方法同样验证了对数正态分布假定在RC框架易损性分析中的适用性。

5.4 灵敏度分析

上节的易损性分析中，取相互作用因子N=2，论述了本文所提方法的计算过程和精度。孙鸿宾等[9]指出，N反应了不同EDP性能极限状态之间的相关性，N越大，相关性越弱，失效域面积越大。因此本节通过灵敏度分析讨论N的值对易损性曲线的影响。分别再取经验值N=1,5,10，其余参数不变，最大熵二次四阶矩法和MC法所得易损性曲线如图5所示。

可以看出，在四种性能极限状态下，随着N增大，易损性曲线逐渐下移，说明破坏概率越小。因此若不考虑性能极限状态之间的相关性，会明显高估结构的抗震能力。在不同N下，基于最大熵二次四阶矩法所得易损性曲线与MC法都基本重合，再一次印证了本文所提方法的计算精度。

6 总 结

本文考虑了结构的联合极限状态，建立了基于最大熵二次四阶矩可靠度理论的易损性分析法，得到了易损性曲线，并与传统基于对数正态分布假定的易损性曲线进行对比，结论如下。

(1) 考虑地震激励的不确定性，不对EDP的分布进行人为假定，通过统计分析获得EDP的前四阶矩，并计算极限状态方程的前四阶中心矩，所得易损性曲线与传统对数正态分布假定的易损性曲线基本重合，说明本文所提方法具有很高的精度，同时也验证了对数正态分布的假定在RC框剪结构易损性研究中的正确性。

(2) 基于联合极限状态的易损性研究，利用随机变量的前四阶矩作为约束条件，建立最大熵概率密度函数，将二重积分简化为一维积分，同时避免了MC法大量的数值模拟计算，计算效率很高。

(3) 在联合性能极限状态方程中，相互作用因子N的取值会对失效概率产生很大影响。N越大，说明不同EDP性能极限状态的相关性越弱，忽略EDP的相关性将不利于工程安全。