大规模多点基础激励随机振动并行计算研究
宁民亮, 范宣华*, 王柯颖, 陈 璞
(1.中国工程物理研究院总体工程研究所,绵阳 621999;2.北京大学 力学与工程科学系,北京 100871)
1 引 言
在对航空航天、大型军事和民用设施等复杂装备进行可靠性评估时,有限元模型的自由度动辄数千万甚至数亿,需要使用具备超大规模计算能力的软件来分析整个系统的结构动力学特性。当前市面上广泛使用的有限元软件如ANSYS和ABAQUS等,由于底层框架的限制,其自由度计算规模仅能达到百万量级,且相关技术受到严格禁运,难以满足对复杂装备进行高效数值模拟的迫切需求[1,2]。
并行计算是解决超大型装备动力学分析等挑战问题的关键技术之一[3,4]。2004年,美国发布白皮书将高性能计算作为提高和维系其制造业市场竞争力的王牌[5]。近年来并行技术不断得到发展,国外已研发出多款具备高性能并行计算能力的软件。如美国圣地亚实验室基于SIERRA框架研发的结构动力学模块SIERRA/SD[6],具备模态和振动分析常用类型的超大规模计算能力,最大自由度计算规模已经可以上亿,但相关软件代码对国内完全禁运;西班牙瓦伦西亚大学结合PETSc数据框架研发的SLEPc软件[7],集成了大量的特征值并行计算功能,可实现不同行业的模态分析大规模并行计算能力。该软件重点针对结构动力学的模态分析功能,不具备其他结构动力学分析功能。
面对技术封锁,国内近些年也在积极推动自主力学分析软件的研发工作,国家多个部委也设置了软件自主化项目予以倾斜资助。国内相关研究以紧跟国际前沿、集成开发创新为主,但研发进度和计算能力与发达国家还存在较大差距。如张林波等[8]基于PHG平台开发的并行自适应结构分析模块PHG-Solid,具备数亿自由度以上的大规模自适应网格划分能力以及静力学线性方程组求解能力,在结构动力学方面支持模态分析并行计算,但尚不具备其他结构动力学分析能力;徐良寅等[9]研发的SiPESC软件,采用平台+插件的运行架构,方便用户在此框架上进行二次开发,其中SiPESC.FEMS模块具备模态分析、频响分析和随机振动分析等功能,在多个领域结构分析方面发挥了重要作用,目前SiPESC的程序运行主要以串行模式为主,最大分析能力仍受到一定限制。
中国工程物理研究院从2007年开始进行结构力学大规模并行计算研究,基于院内JAUMIN框架[10]自主研发形成了并行非结构网格有限元计算平台PANDA[11]。并在该计算平台上完成了模态分析、谐响应分析和响应谱分析等多个动力学分析模块的开发和应用研究[12,13]。本文在已有研究基础上,针对多点基础激励随机振动分析问题,开展了理论推导、算法设计以及模块研发等相关工作。最终测试结果表明,研发的多点随机振动分析模块拥有商业软件不具备的超大规模运算能力。
2 相关理论和求解优化
2.1 多点基础激励随机振动理论
多点基础激励结构动力学方程[14]为
(1)
式中M,C和K为结构自由节点的质量阵、阻尼阵和刚度阵,MC,CC和KC为支承和结构耦联部分的质量阵、阻尼阵和刚度阵,MR,CR和KR为支承约束节点的质量阵、阻尼阵和刚度阵,u为结构的绝对位移,可以分解成准静态位移us和动力相对位移ud两部分,uR为支承的绝对位移,R为支撑反力。
结合文献[13]相关推导过程,式(1)最终可表示为准静态响应方程和动态响应方程两部分。
(2)
式中uR,l为第l个基础激励位移,al为位移影响系数向量,表示在第l处约束沿激励方向施加单位位移引起的结构自由节点各自由度的位移向量,N为基础激励的个数。
对大规模装备进行动力学并行计算时,一般采用模态叠加法进行分析,以避免直接矩阵分解带来灾难性存储和大量并行通信。用模态分析获得的m阶模态特征对{(ω1,φ1),(ω2,φ2),…,(ωm,φm)}进行解耦,可得式(2)动态部分对应的模态解耦方程为
(3)
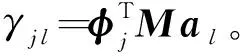
(4)
式中Sp q(ω)为第p处和第q处基础加速度激励对应的功率谱密度,Sd,k(ω),Ss,k(ω)和St,k(ω)分别对应第k个自由度的动态位移自功率谱密度、静态位移自功率谱密度和总位移功率谱密度,Sd s,k(ω)为动态和准静态位移功率谱密度的交叉项,Hj(w)为式(3)对应的频响函数,φj,k为第j阶模态对应的第k个元素值,ap,k为第p处单位基础位移引起的第k个自由度的准静态位移值。式(4)中Hj(w)和Sd s,k(ω)的具体表达式为
(5)
式(4)建立了位移功率谱密度表达式,相应的速度和加速度自功率谱密度分别为位移自功率谱密度的ω2和ω4倍。获得相应关注点的响应功率谱密度曲线后,对曲线对应频段进行积分开方后可获得对应关注点的等效均方根响应。
2.2 随机振动应力分量和Mises等效应力求解
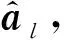
随机振动的Mises等效应力求解相对于静动力学的确定性问题求解更为困难,这是因为载荷输入给出的是统计特性,而且响应本身也是统计性数据[15]。此外,Mises应力是各应力分量的非线性函数,前面计算位移、速度、加速度以及应力分量响应的理论方法无法直接应用于Mises应力的计算[16]。有限元分析中,节点的应力分量可以写成矩阵形式σ={σx,σy,σz,τx y,τy z,τx z}T,而Mises应力σM与应力分量σ的关系满足:
(6)
式中矩阵B的表达式为
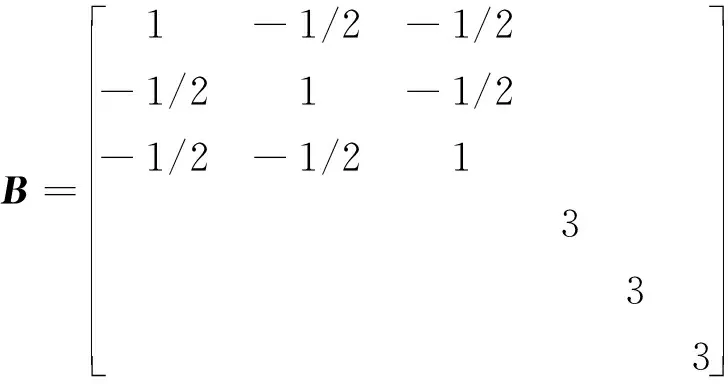
(7)
对于第k个节点,结合文献[15,16]处理方法,可以给出与式(4)对应的动态和准静态Mises应力自功率谱密度为
(8)
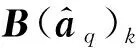
2.3 求解过程的优化
将N个基础载荷的功率谱密度以谱矩阵形式给出
(9)
式中每个元素代表一条谱曲线,对角线元素对应各基础激励的自谱,非对角线元素对应不同基础激励之间的互谱,不相关载荷之间的互谱为0。在前述核心理论公式的计算过程中,不考虑零元素,只针对非零元素进行循环,可减少计算量。
在对全场均方根响应进行求解时,按照均方根响应的定义,需求解完全部自由度对应的自功率谱密度曲线后,再对自功率谱密度曲线进行积分求解。以动态位移自功率谱密度为例,其均方根响应表达式为
(10)
对于n自由度系统,p个频率离散点,全场均方根响应对应的浮点运算量为(n×m×m×p×N×N),如此计算需要的浮点运算量非常巨大,甚至超出模态分析计算时间的数倍之多。优化过程中发现,均方根积分求解的模态振型与积分频率无关,因而可以将积分项进行分离变换。以动态位移响应为例,将式(10)第k个自由度的动态位移均方根积分公式变换为
(11)
式中Qi j实际是模态坐标空间中的一个m×m阶协方差矩阵对应的第i行第j列的元素值。经过处理变换后得到的式(11),分别以二重求和作为基本运算单位取代式(10)的四重求和运算,只需要(n×m×m+p×N×N)次浮点运算即可。此外需要存储一个模态空间下m×m阶的模态协方差矩阵,这对于大规模计算来说占用的存储量几乎可以忽略。以上优化过程可以理解为,将整体积分项中与频率相关积分变量项和空间变量进行分离,在较小的模态空间内获得积分结果,并作为模态贡献在物理空间内进行叠加,从而将原来的多个乘法浮点运算转换成两个较小乘法浮点运算量之和,大大降低了计算量。
对于上述优化,举例说明如下,假设结构自由度数n为10000,频率离散点p为1000,多点激励个数N为10个,模态参与阶数m为100阶,则优化前的基本运算单位对应的浮点计算量为1013,优化后浮点计算量仅为108+105,减少的单位浮点计算量可以呈现接近5个量级的减少,即原来需要100000秒完成的计算,优化后只需要1秒左右便可完成。
3 随机振动的算法设计和并行实现
3.1 算法设计
根据第2节推导的理论公式,设计多点基础激励随机振动分析的算法如下。
(1) 建模和矩阵离散。简化实际工程结构,建立有限元模型并划分网格。在JAUMIN框架下进行区域分解和必要的网格自适应加密;在PANDA平台下建立相应的质量阵和刚度阵。
(2) 获取模态信息。建立广义特征值问题并开展模态分析,获得各阶模态频率和正交归一化的模态振型,该部分工作已在PANDA中实现[11]。
(3) 求解位移影响系数向量al。借助PANDA静力学并行分析模块,分别求解N个不同约束沿激励方向施加单位位移引起的结构响应,获得一系列位移向量al。
(4) 计算振型参与系数γl j。利用质量阵、模态振型和位移向量al计算不同模态坐标系下的振型参与系数γl j。
(5) 计算自功率谱密度和全场均方根响应。以关注节点的每个自由度为一次循环,以给定的频谱曲线离散频率为二次循环,进行每个离散频率下的自功率谱密度和均方根响应计算。
① 利用曲线离散频率及各阶模态阻尼比,建立解耦方程,算出相应的频响函数。
② 根据功率谱密度、频响函数值和振型参与系数,按照前面的理论公式计算动态位移、准静态位移以及总位移的自功率谱密度。
③ 按照模态位移振型获得的应力振型计算各节点应力分量的自功率谱密度。
④ 计算模态坐标系下的协方差矩阵,并根据推导的理论公式分别计算各部分位移(速度和加速度)的等效均方根响应以及不同节点位置的各应力分量和Mises应力的等效均方根响应。
(6) 输出关注节点的自功率谱密度曲线以及全场等效均方根值。
以上的算法设计中,可以求解结构部分关注点或全部节点自由度的自功率谱密度和响应均方根值。各自由度的求解根据并行区域分解的结果可以在各自进程内分别求解,属于天然并行模式。其中,区域分解基于JAUMIN框架完成,通过在不同子区域设置映像区的方式实现相邻子区域之间的数据交换和通信,具体实现方式参见文献[10]。
3.2 并行实现
本文开展的大规模多点基础激励随机振动并行实现主要基于JAUMIN框架和PANDA平台,采用C++和MPI编程完成。JAUMIN底层框架具有优异的数据并行处理和矩阵运算能力,在并行实现过程中,搭配前后处理软件,负责完成数据块之间的通讯和管理、建模以及区域分解等工作;PANDA平台则负责构建相应的质量阵和刚度阵并组装,然后调用研发的随机振动分析模块开展求解工作。关于JAUMIN框架和PANDA平台的具体介绍可参见文献[10,13],在此不做赘述。
本文进行的随机振动相关算法设计是基于模态叠加法开展的,其总体架构设计如图1所示。随机振动分析结合模态参与系数、频响函数以及谱曲线输入等,通过模态叠加计算响应,然后导向输出流。其中各阶振型参与系数根据求解的准静态位移向量,并结合各阶模态振型来确定;谱线管理器管理着多个自谱和互谱,为模态叠加过程提供谱曲线输入。
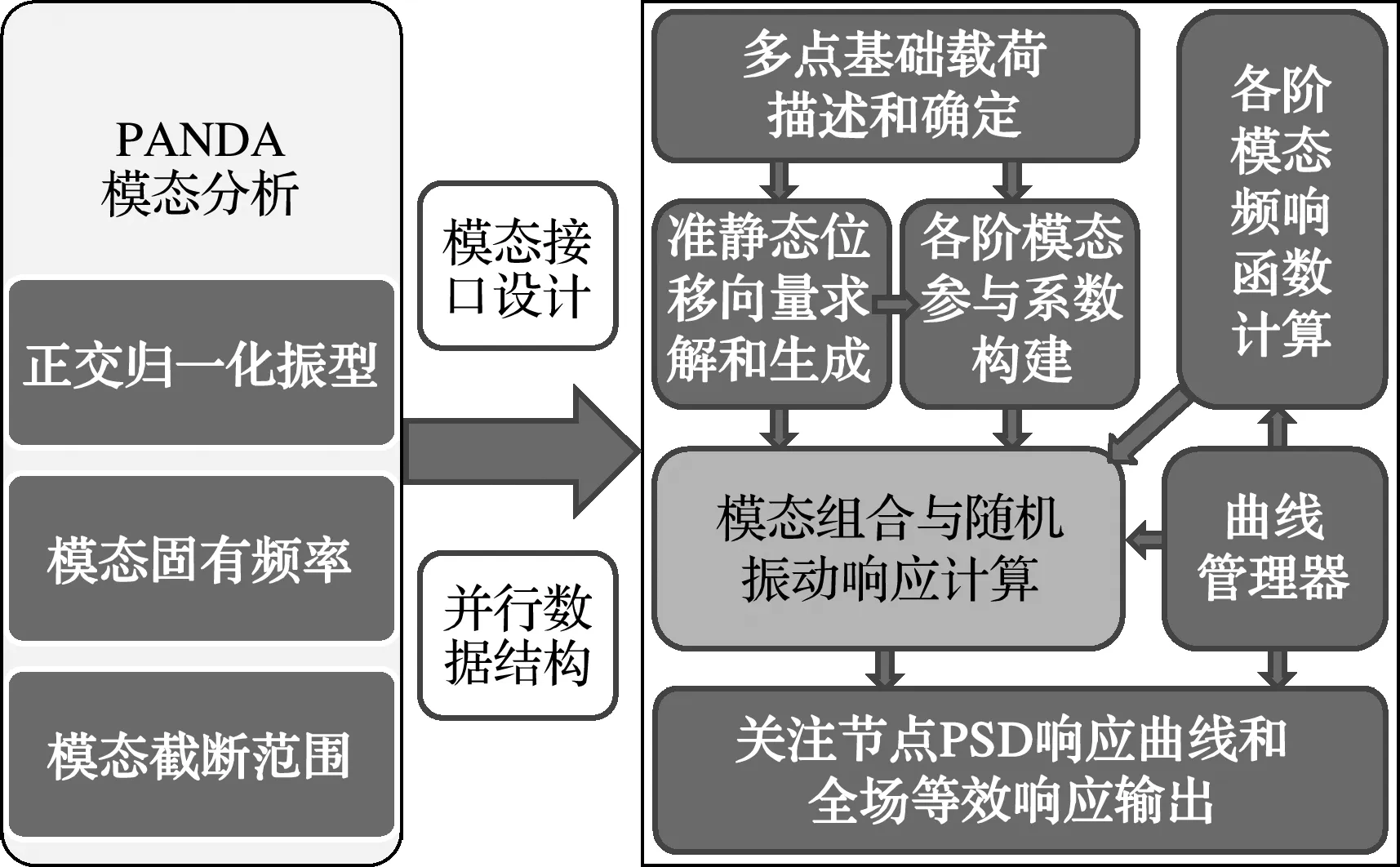
图1 多点随机振动分析架构设计
在多点基础激励随机振动并行求解模块中,首先通过JAUMIN框架进行区域分解,构建分布式质量矩阵和刚度矩阵,不同区域对应的矩阵数据发送到不同的CPU进程,PANDA对这些分布式矩阵数据调用模态分析并行计算功能获得模态频率和振型等相关信息,之后结合载荷曲线和模态信息构建模态参与系数,并在不同子区域内进行结构随机振动响应的计算。随机振动模块主要包含以下四个C++类。
谱曲线管理类。负责处理多个不同基础激励的谱曲线,包括曲线的描述和离散等。曲线离散方式支持均匀离散和根据模态固有频率及模态阻尼比的自适应离散,这些离散结果在振动响应求解时调用。
振型参与系数类。根据模态振型以及基础载荷系数向量计算各阶振型参与系数,这些振型参与系数以数组的形式存储,在响应求解时调用。
随机振动响应计算类。该类用于各关注点的PSD响应曲线计算以及全场的等效均方根响应计算,该类的输入包括模态参与系数、频响函数、各阶模态振型和输入载荷PSD曲线。
输出类。该类用于关注点PSD曲线和全场等效均方根响应的输出。相关计算数据按照JAUMIN框架后处理软件规定的数据格式进行输出,便于曲线绘制和全场云纹图显示。
在整个分析流程中,网格区域的划分、质量阵和刚度阵的构建以及模态分析和响应求解是主要的并行阶段。其中模态分析主要依靠PANDA平台的模态分析功能实现求解,目前支持Krylov-Schur[17]与Jacobi-Davidson[18]两种主流并行求解算法。
4 数值算例
4.1 Benchmark算例
采用不规则扇体作为Benchmark算例。扇面尺寸左边宽为1.75 m,右边低端宽为1.25 m,体厚度为0.6 m,有限元模型如图2所示。模型全部以六面体单元划分,采用单一材料,对应的弹性模量为210 GPa,密度为7800 kg/m3,泊松比为0.3。将模型两端面固定,作为施加加速度激励的基础,沿端面法向施加两个大小不同的加速度激励,频率范围为1 Hz~2000 Hz。激励曲线采用白直谱,右端幅值为1,左端幅值为2。两端激励互谱实部和虚部幅值分别为0.7和1.2,取前20阶模态进行模态叠加。选取模型中部五角星标记点作为关注点。
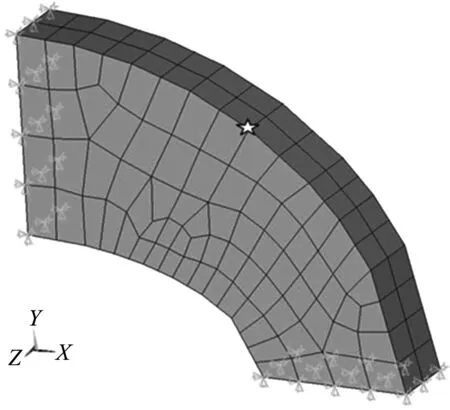
图2 扇形体有限元模型
图3和图4是利用PANDA和ANSYS算出的标记节点的位移自功率谱密度曲线对比情况。可以看出,不管是动态位移还是绝对位移,两个软件算出来的自功率谱密度曲线都基本重合。关注点的速度响应以及加速度响应曲线和位移曲线仅差一个频率平方的倍数,两个软件计算结果亦完全一致,在此不再列出。
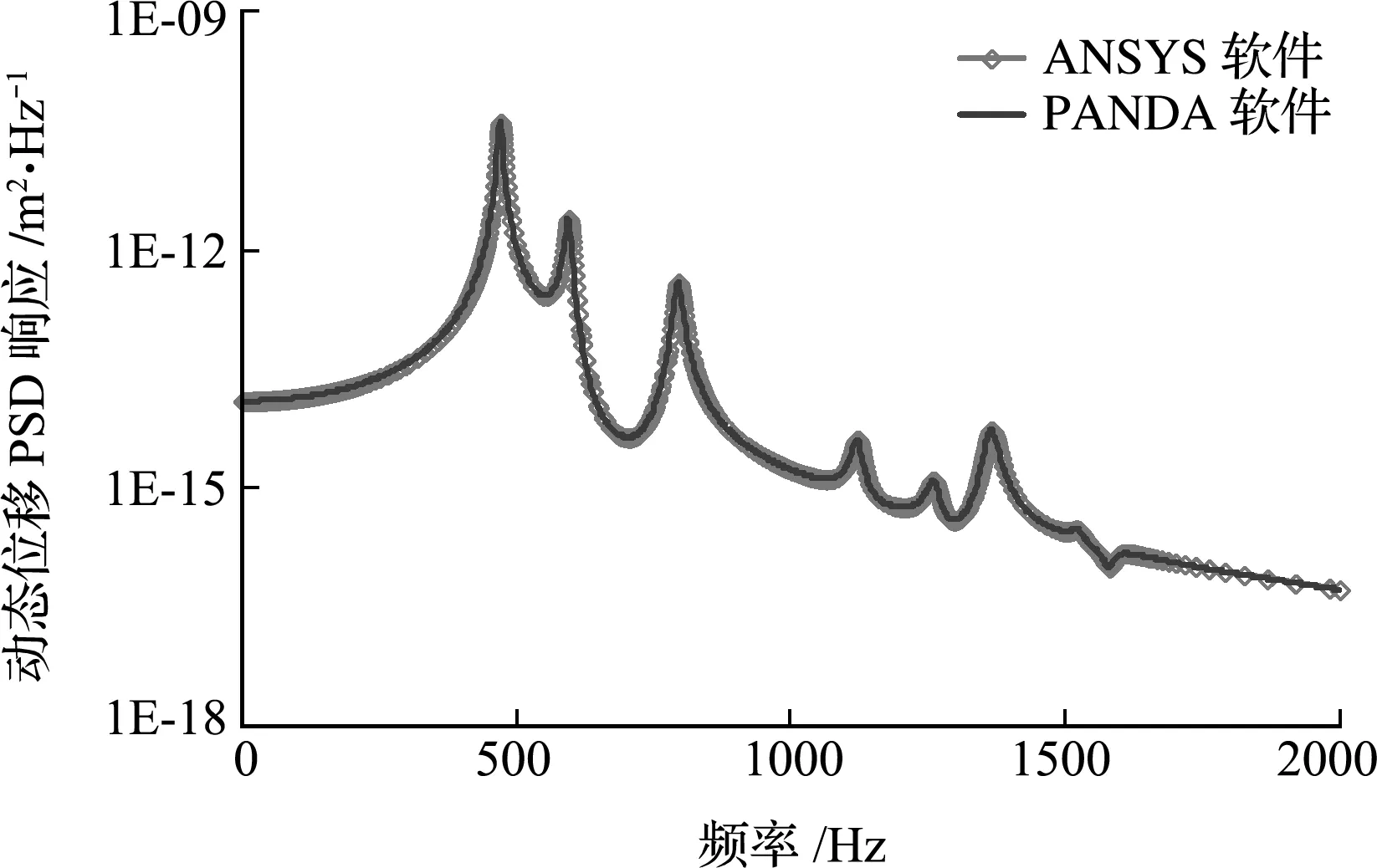
图3 关注点动态位移自功率谱密度对比

图4 关注点绝对位移自功率谱密度对比
图5和图6是PANDA和ANSYS关于全场等效位移云图和全场Mises应力云图的对比。可以看出,两种软件关于等效均方根响应的计算结果在数值分布、最大值以及最大值出现的位置都非常吻合。这说明前面推导的均方根响应公式以及对应的算法程序是正确的。计算时间方面,在同一配置的台式机上,本算例PANDA串行计算的时间为1.05 s,ANSYS的运行时间为1.92 s。这是因为,PANDA软件基于Linux系统安装,运行过程可以充分利用机器内存完成计算;ANSYS等商业有限元软件基于Windows系统,在软件运行过程中需要从硬盘读取数据和存放中间变量信息,内存利用率较低。这使得PANDA计算时间远低于ANSYS。随着计算规模的增大,PANDA的计算时间优势较ANSYS更为明显。
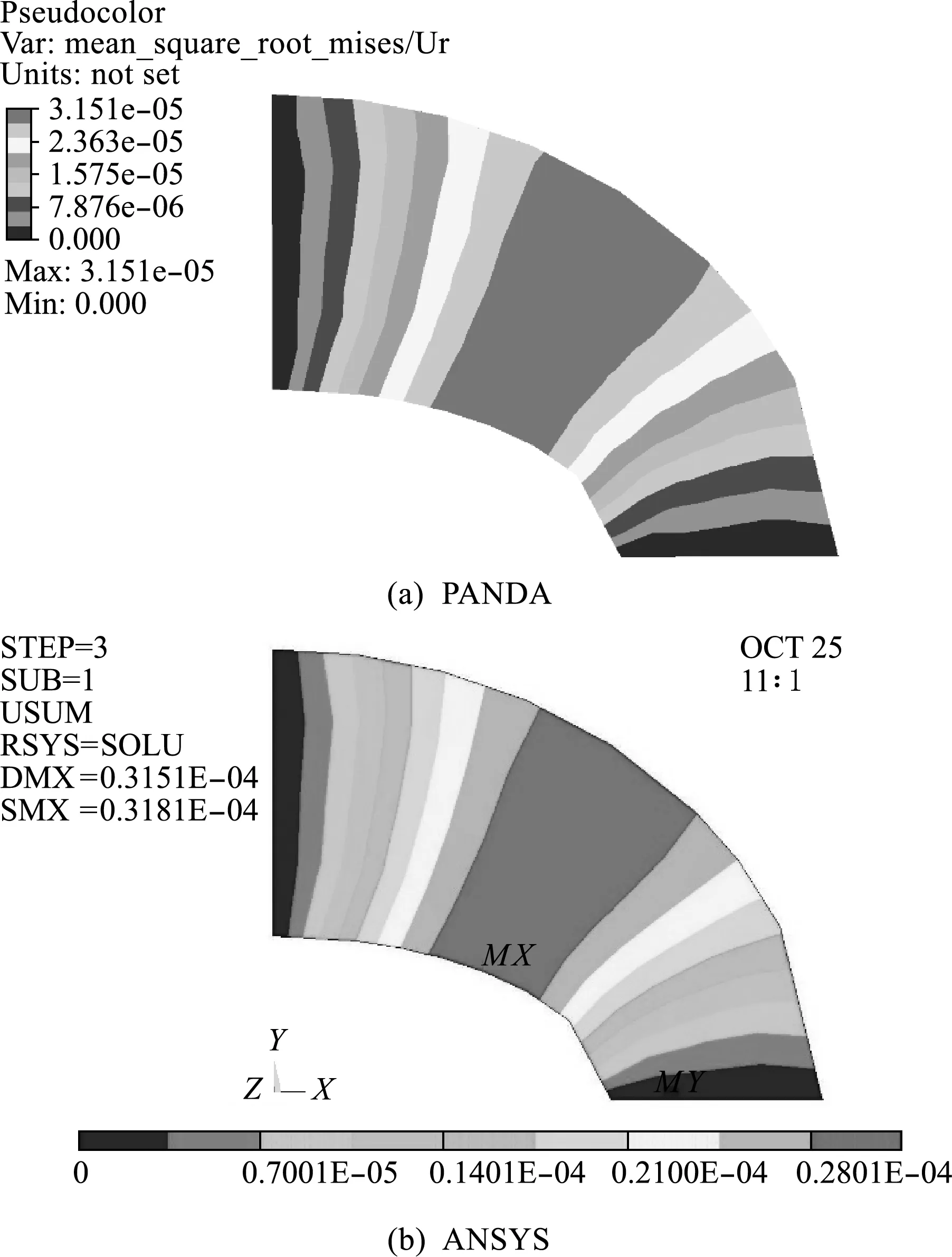
图5 全场位移等效均方根响应对比

图6 Mises等效应力均方根响应对比
4.2 大型光机测试算例
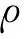
任取模型上某一节点,图8和图9是PANDA和ANSYS关于该点Y方向动态位移和绝对总位移自功率谱密度曲线的对比。可以看出,两个软件计算的响应曲线基本一致,再一次验证了研发模块的正确性。图10给出了光机装置全场Z向动态位移等效均方根位移云图的计算结果。二者的云图亦保持一致,略微差别主要来自不同的频率离散策略带来的积分误差。
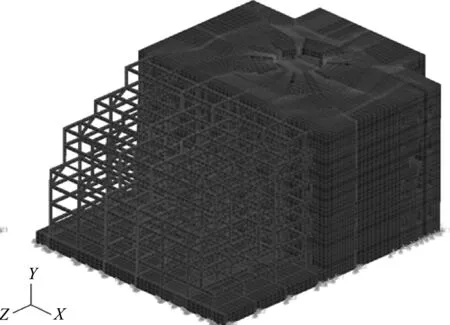
图7 某大型光机有限元模型
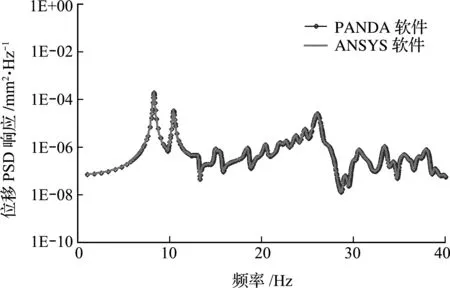
图8 动态位移自谱曲线对比
图9 总位移自谱曲线对比

图10 光机装置Z向动态位移云纹图对比
为测试多点随机振动分析模块的并行可扩展性,对光机结构进行网格自适应加密3次后,得到了11.88亿自由度计算规模,并在天河超大并行机群上开展了多达上万核的并行扩展测试。表1展示了使用不同CPU核数对应的计算时间和并行效率。可以看出,对于11.88亿自由度,万核相对模型能够计算的2048核并行效率高达80%以上,说明了研发模块具备优异的并行可扩展能力。表2 给出了光机装置在10240个CPU核下各个主要求解环节的时间统计情况,可以看出,模态分析占据了整个求解时间的99%以上,随机振动响应求解只占了0.2%的时间,充分说明了2.3节中算法和模块求解优化带来的巨大计算效益。
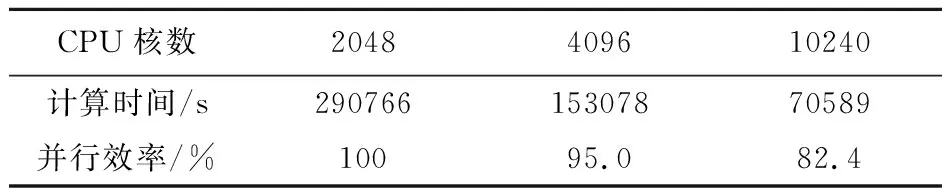
表1 光机装置并行可扩展性测试结果
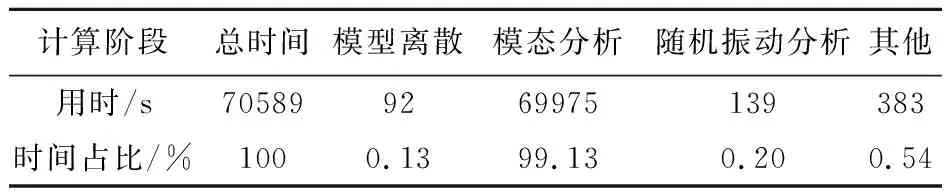
表2 光机装置万核计算各主要环节时间统计
5 结 论
本文从随机振动的基本理论入手,系统推导了基于模态叠加法的多点基础激励随机振动分析理论体系,对求解流程进行了必要的优化,在此基础上完成了相应的算法设计和模块研发。将算例结果与商业有限元软件进行对比,验证了研发模块的正确性;对该模块进行了并行可扩展性测试,结果显示该模块具备优异的并行计算可扩展能力。
结合开展的算例测试结果可以看出,开发的多点基础激励随机振动分析模块能够实现位移、速度、加速度以及应力等典型动力学响应量的功率谱密度计算和等效均方根计算,并且可以达到与商业有限元软件一致的计算精度,该模块功能对单点基础激励的情形同样适用。对于商业软件无法计算的上亿自由度规模,PANDA软件通过并行求解技术完全可以胜任,目前测试得到的最大计算规模可以达到10亿自由度以上,其并行计算可扩展能力比现有商业软件更强。

