纤维再生混凝土单向板承载力极限状态方程及可靠度计算

符勇强， 方圣恩*,2， 林志平

(1.福州大学 土木工程学院，福州 350108； 2.福州大学 土木工程防震减灾信息化国家地方联合工程研究中心，福州 350108；3.福建省高速公路集团有限公司，福州 350001)

1 引 言

我国每年因生产建设对砂石和土地等自然资源的消耗巨大。旧建(构)筑物拆除时产生的混凝土废料数量庞大，主要采取就地掩埋的方式，容易污染环境和浪费资源[1]。而混凝土废料经过一系列处理可以加工成再生骨料，然后加入胶凝材料、水和外掺料等拌制成再生混凝土[2]，有利于资源回收利用，符合当前我国的绿色发展理念。

与天然碎石相比，再生骨料吸水性大，在破碎过程中会受到损伤，骨料内部细观结构复杂，裂纹多，强度变异性大,限制了再生骨料混凝土在受力结构和构件中的运用[3]。文献[4]对不同取代率下再生混凝土RC(recycled concrete)单向板进行试验研究，通过试验数据拟合得到RC单向板承载力计算公式。同时，文献[5]表明，随着RC强度提高，RC组合框架承载力提高不大，但变形能力逐渐降低。对于RC梁受弯和受剪时的可靠指标，可通过合理增加配筋量来保证与普通混凝土OC(ordinary concrete)梁一致[6]。

通过在再生骨料混凝土中添加纤维，制备纤维增强再生混凝土FRC(fiber-reinforced recycled concrete)，能有效提高再生混凝土的力学性能[7-9]。研究指出，纤维的加入提升了再生混凝土受弯构件的耐久性和承载力[10]。文献[11]研究了纤维掺量和长度对FRC本构规律的影响。与此同时，文献[12]对FRC单向板进行受力试验研究，指出FRC单向板承载力较RC有所提高，略低于OC单向板。在混凝土开裂→钢筋屈服→极限承载过程中，纤维和钢筋能够协同工作。但是，对于FRC构件的可靠度计算，仍需参考普通混凝土，没有形成完整的计算方法，缺乏针对性的理论公式。

有鉴于此，本文基于现行规范和已有的研究成果，分别对OC单向板、RC单向板以及FRC单向板进行可靠度分析。考虑了FRC单向板抗弯承载力的影响因素，根据FRC本构关系，确定了FRC受压区等效矩形应力图系数，进一步推导了FRC单向板的抗弯极限状态方程。在上述成果的基础上，从可靠度的角度出发，基于验算点法推导了OC，RC以及FRC单向板的可靠度计算公式。以期为纤维增强再生混凝土板的可靠度设计以及计算提供参考，从而推动其在工程中的可靠应用。

2 FRC单向板受弯承载力极限状态方程

分别对OC单向板、RC单向板以及FRC单向板承载力计算公式进行推导，确定板的抗弯极限状态方程。

可以单筋矩形截面受弯构件分析OC单向板的承载力，确定单向板的破坏形式，即纵向钢筋屈服，同时受压区混凝土压碎。考虑截面尺寸、混凝土强度、钢筋强度以及荷载等随机变量影响承载力的计算，引入计算模式不定性系数K[13]。

OC单向板受弯承载力计算公式和极限状态方程Z为

fyAs=α1fcbx

(1)

(2)

式中Mu为极限弯矩，α1为等效矩形应力图系数，fc和fy为混凝土轴心抗压强度和钢筋抗拉强度，As为钢筋截面面积，b和h0分别为截面宽度和有效高度，SG为恒载，SQ为活载。

对于RC单向板，文献[4]采用与OC单向板相同配合比(骨料取代率γ为0,50%和100%)进行分析，提出了RC单向板受弯承载力计算公式，引入参数μ=Ms/Mt，Ms为数值模拟值或理论计算值，Mt为试验实测值。以普通混凝土为标准，提出μ关于γ之间的函数表达式为

μ=1-0.2168γ-0.0063γ2

(3)

Mt≤μα1fcbx(h0-x/2)

(4)

式中μ为理论计算值与试验实测值的比值。

本文取γ=50%，通过式(3)计算得到μ=0.89，建立RC单向板受弯承载力的计算公式和极限状态方程Z为

fyAs=α1fcbx

Mu=0.89fyAs(h0-x/2)=

(5)

SG-SQ

(6)

对于FRC单向板，以聚丙烯纤维为例，文献[11]对FRC本构关系进行研究，γ=50%，聚丙烯纤维体积掺量为0.8%，通过试验数据拟合得到本构参数b=1.394，a=3.020。本构关系中，考虑混凝土的非线性发展，应力应变关系曲线由上升段和下降段组成，采用如下分段有理分式表达。

(0≤x<1) (7)

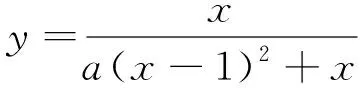
(8)

同时，文献[12]对FRC单向板进行试验，但并未给出FRC单向板承载力计算公式。根据式(7，8)确定FRC的本构方程，通过积分得到FRC应力应变曲线与横轴极限压应变εc u为基准所围面积Cc u=0.0022，以及所围面积形心到坐标原点的距离yc u=0.002，进而求得系数k1=0.667，k2=0.6061，由公式α1=k1/2(1-k2)计算得到α1=0.85[15]。

建立FRC单向板受弯承载力计算公式和极限状态方程Z为

fyAs=0.85fcbx

Mu=fyAs(h0-x/2)

(9)

(10)

式中a和b为聚丙烯纤维再生混凝土的本构参数，εc u为极限压应变，Cc u和yc u为混凝土压应力-应变曲线所围面积以及面积形心到坐标原点的距离，k1和k2为聚丙烯纤维再生混凝土的压应力-应变曲线系数。

对于其他纤维再生混凝土，亦可通过本构关系确定极限状态方程，按上述方式进行类似推导。

3 FRC单向板受弯极限状态可靠度计算公式

分别对OC单向板、RC单向板以及FRC单向板处于承载力极限状态时的可靠度计算公式进行推导，用于计算单向板抗弯极限状态时的可靠度。

3.1 OC单向板可靠度计算

根据式(2)确定的极限状态方程计算其梯度函数Z′，令

m=fyAs,n=KfyAs/fcb=Km/fcb

(11)

Z=Kh0m-0.5mn-SG-SQ

(12)

Z′=[h0m-0.5m2/fcb,Km,Kh0As-Asn,

0.5mn/fc,Kh0fy-fcn,-1,-1,0.5mn/b]

(13)

式中m和n为设定简化函数。

式(12)在极限状态某点x*处按Taylor级数展开并保留一次项，则Z的均值为

(14)

将各自变量方差乘以梯度函数平方和开方，则Z的方差为

(15)

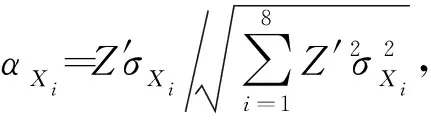
(16)

将式(16)的β与分母相乘并化简,

(17)

得到新的验算点：

(18)

式中Z′为梯度函数，μZ和σZ分别为Z的均值和方差，x*初始迭代时可取μXi，αXi为灵敏度系数，μXi和σXi分别为自变量均值和方差。

3.2 RC单向板可靠度计算

根据式(6)确定的极限状态方程计算其梯度函数Z′，令

m=fyAs,n=KfyAs/fcb=Km/fcb

(19)

Z=0.89Kh0m-0.5×0.89mn-SG-SQ

(20)

Z′=[0.89h0m-0.45m2/fcb,0.89Km,

0.89Kh0As-0.89Asn,0.45mn/fc,

0.89Kh0fy-0.89fcn,-1,-1,0.45mn/b]

(21)

根据式(20,21)确定RC单向的板极限状态方程和梯度函数，按上述OC单向板计算流程(14～18)计算RC单向板的可靠度。

3.3 FRC单向板可靠度计算

以聚丙烯纤维为例，根据式(10)确定的极限状态方程计算其梯度函数Z′，令

m=fyAs,n=KfyAs/0.85fcb=Km/0.85fcb

(22)

Z=Kh0m-0.5mn-SG-SQ

(23)

Z′=[h0m-0.5m2/fcb,Km,Kh0As-Asn,

0.5mn/fc,Kh0fy-fcn,-1,-1,0.5mn/b]

(24)

根据式(23,24)确定FRC单向板的极限状态方程和梯度函数，按上述OC单向板计算流程(14～18)计算FRC单向板的可靠度。

4 试验算例

本文试验单向板模型选自文献[12]，分别对两块聚丙烯纤维增强的FRC板、一块RC板及一块OC板进行静载试验，γ=50%，聚丙烯纤维体积掺量为0.8%。板的尺寸为2400 mm×1600 mm，净跨为2000 mm，板厚60 mm，混凝土采用C40，钢筋为III级钢，间距200 mm。铸铁块加载，模拟均布荷载作用。当加载至20 kN左右时，各板受拉钢筋开始屈服。最终OC,RC和FRC单向板的极限承载力分别为37 kN,33 kN和35 kN。可见加入纤维后,板的极限承载力有所提升。

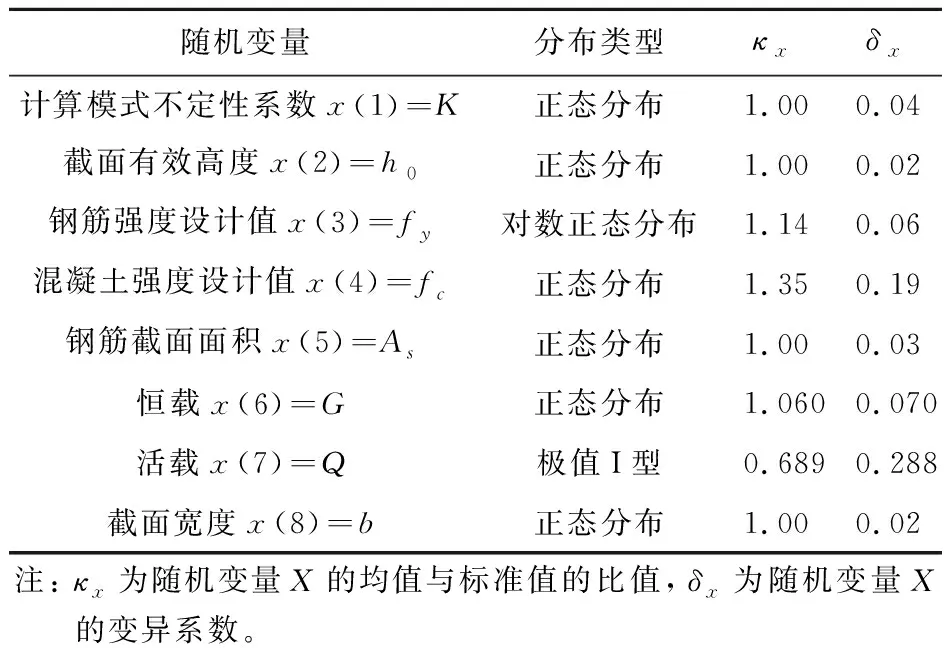
表1 单向板随机变量统计参数[14]

4.1 单向板可靠度计算

加载至20 kN左右时(受拉钢筋开始屈服)，恒载(板自重)均值为

μSG=1.06×1.2=1.27 kN·m=1270000 N·mm

活载均值为

μSQ=0.689×5.0=3.445 kN·m=3445000 N·mm

混凝土强度均值为μfc=1.35×19.1=25.785 N/mm2，钢筋抗拉强度均值μfy=456 N/mm2，截面有效高度均值h0=46 mm，钢筋面积均值As=453 mm2，截面宽度均值b=1600 mm，对于OC单向板钢筋屈服时状态，采用式(2)计算可靠度为

Z=1×456×453×46-1×4562×4532/2×

25.785×1600-1270000-3445000

进而根据式(11～18)编制可靠度计算程序，计算得到OC单向板钢筋屈服时，可靠度指标β=3.3165。

对于RC单向板钢筋屈服时状态，采用式(6)计算可靠度为

Z=0.89×456×453×46-0.89×4562×4532/2×

25.785×1600-1270000-3445000

得到RC单向板钢筋屈服时,可靠度指标β=2.8202。

对于FRC单向板钢筋屈服时状态，采用式(10)计算可靠度为

Z=1×456×453×46-1×4562×4532/2×0.85×

25.785×1600-1270000-3445000

得到FRC单向板钢筋屈服时，可靠度指标β=3.2746。

规范[14]规定，对于普通住宅和办公楼，为保证结构具有一定的安全储备，(梁、柱和板)延性破坏时的可靠度指标β≥[β]=3.2。由计算结果可知，OC和FRC单向板延性破坏时的可靠度均大于规定值。因此，按式(9，10)对FRC单向板进行抗弯承载力设计和可靠度设计是满足要求的。

继续加载至极限承载力时，恒载(板自重)均值为

μSG=1.06×1.2=1.27 kN·m=1270000 N·mm

OC单向板活载均值为

μSQ=0.689×9.25=6.37325 kN·m=

6373250 N·mm

RC单向板活载均值为

μSQ=0.689×8.25=5.68425 kN·m=

5684250 N·mm

FRC单向板活载均值为

μSQ=0.689×8.75=6.02875 kN·m=

6028750 N·mm

按上述计算流程计算单向板处于极限承载力状态时的可靠度指标，得到OC单向板β=0.8318，RC单向板β=0.7600，FRC单向板β=0.9743。

对比RC和FRC板不同承载时的可靠度，可见纤维的加入对板的抗弯刚度起到了强化效果，提高了RC单向板的安全性。

4.2 活恒载效应比和纵筋配筋率影响分析

上述算例中，保持其他参数不变，分析活载与恒载效应比SG/SQ对可靠度指标的影响，结果如图1所示。可以看出，OC单向板和FRC单向板可靠度相差不大。随着活恒载效应比的增大，即活载效应的比重增大，各板的β值均减小。变异系数对可靠度的影响体现在各自变量的方差取值，这是由于活载变异系数比恒载大，即活载方差大。可见活载变异性越强，对板的可靠度影响也越大。

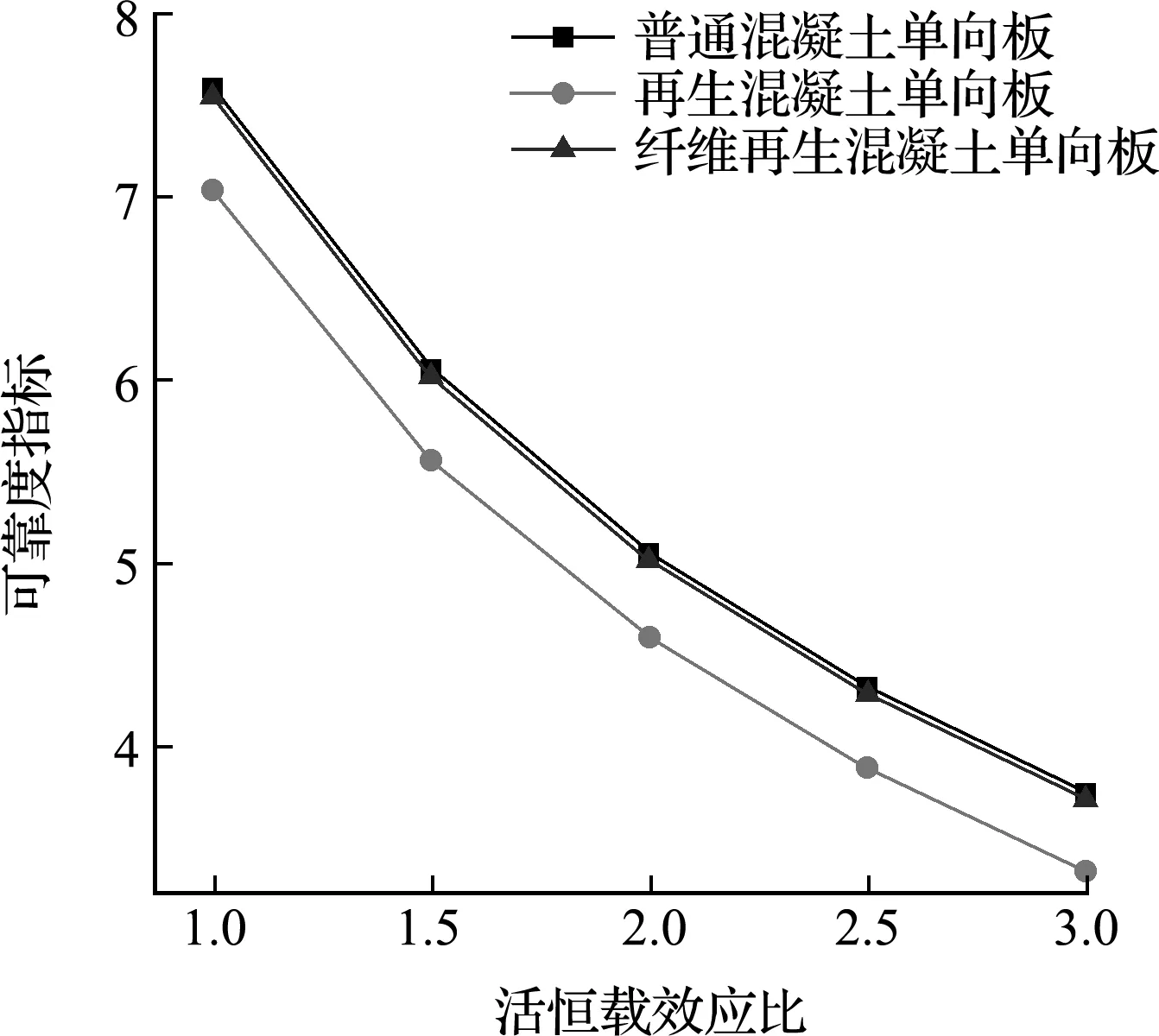
图1 活恒载效应比-可靠度关系曲线

在基准受拉纵筋配筋率ρ=0.47%的基础上，保持其他参数不变，改变极限状态方程中纵筋面积均值及方差取值，进一步分析0.5ρ，1.0ρ和1.5ρ对可靠指标的影响，结果如图2所示。可以看出，随着ρ的提高，OC，RC和FRC单向板的β值均有明显提升，因此纵筋配筋率对单向板的可靠度影响很大。

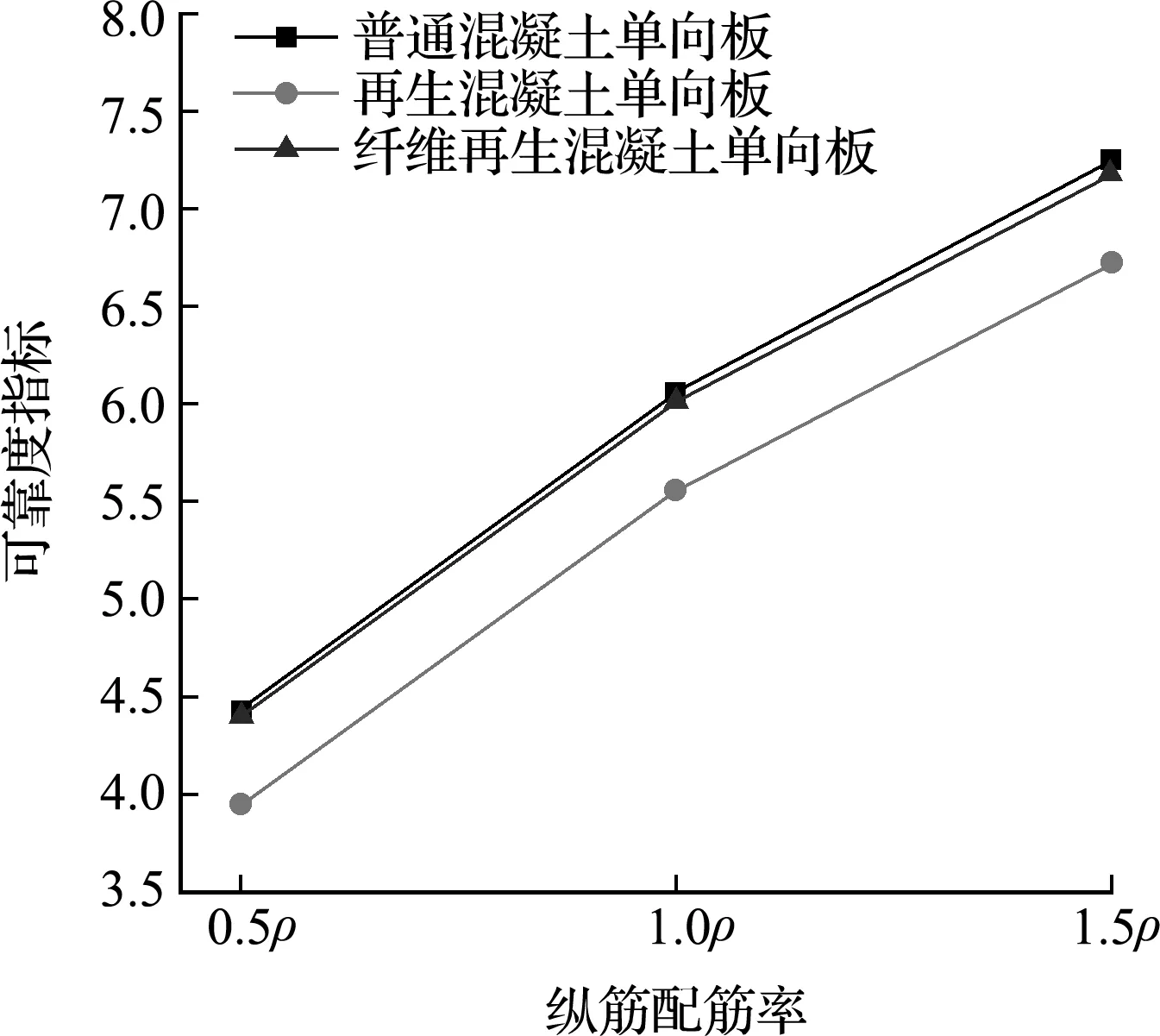
图2 纵筋配筋率-可靠度关系曲线

5 结 论

由于纤维增强再生混凝土板构件受力性能的研究处于开始阶段，可得到的样本数据非常少，此外，关于纤维再生混凝土的设计方法国内外仍不统一，值得后续进一步研究。为此，本文以聚丙烯纤维为例，基于FRC本构关系，结合FRC单向板极限承载状态影响因素，推导了适用于FRC单向板可靠度的计算公式，并对该方法进行了验证，得到如下结论。

(1) OC和FRC单向板延性破坏时的可靠度指标均大于规范值，按式(9，10)对FRC单向板进行正截面受弯承载力设计和可靠度验算均能满足延性要求。

(2) 随着活恒载效应比的增大，OC，RC和FRC单向板的可靠度均减小。OC和FRC板的β值很接近，纤维的加入能够提升RC单向板的可靠度。此外，可以通过提高纵筋配筋率来有效提升单向板的可靠度。

(3) 本文所推导的FRC单向板可靠度的计算公式适用于聚丙烯纤维再生混凝土，对于其他(如碳和玄武岩)纤维再生混凝土，可通过本构关系确定等效矩形应力图系数，进一步确定单向板的极限状态方程，并按本文提出的方法计算可靠度。