载人运载火箭全要素约束迭代制导技术

施国兴，柴嘉薪，胡海锋,2

（1. 北京航天自动控制研究所，北京，100854； 2. 宇航智能控制技术国家级重点实验室，北京，100854）

0 引 言

迭代制导方法的研究已开展多年，理论已经相当成熟。早在美国土星-V 运载火箭的制导方案中已经使用。美国的航天飞机，法国的阿里安火箭等也都采用了迭代制导技术，取得了良好的效果。中国在载人运载火箭上率先研究使用迭代制导方法，并经过多次载人飞行任务考核，将飞船入轨精度提高了一个数量级，为载人空间站工程快速交会对接奠定了技术基础，目前已推广应用于多型在役运载火箭。

上述方法带来的问题是入轨时刻的姿态角必须由制导算法决定，而不能预先确定，否则最后时刻推力矢量的偏差将可能使迭代制导的精度优势荡然无存。而在实际条件下，某些有效载荷存在对地定向以及测控等需求，使得运载火箭需要在高精度入轨的同时，满足一定的入轨姿态和载荷分离前的箭体角速率要求，必须在姿态平稳的条件下释放有效载荷，这就要求在分离前一段时间内箭体不能有大的姿态调整动作，并以有效载荷期望的姿态飞行一段时间后再分离，给箭体完全稳定留出足够时间。

已有迭代制导方法基于最优控制原理，将火箭能量消耗最少的制导控制问题转换为非线性时变系统的最优控制问题，迭代获取最优解析解，但该方法只能满足3个方向速度和2个方向位置共5个约束变量的控制。如果入轨时还需要满足相应的姿态要求，相当于增加了终端姿态约束。这样的需求并非不常见，已有的控制方案中往往依靠在火箭末级配置调姿系统来实现，即在主发动机关机后，增加调姿飞行段。但这将增加系统复杂性和成本，降低可靠性。

本文在迭代制导理论基础上，提出了一种载人运载火箭全要素约束迭代制导技术，该技术在速度、位置约束的基础上，通过引入二次曲线形式的制导程序角和迭代末端程序角常值约束方程，实现对俯仰和偏航姿态的约束；通过引入常值程序角，实现对滚转姿态的约束。解决了载人运载火箭对入轨姿态和分离前的角速度等高要求的工程实际问题，并利用数学仿真对该方法进行深入细致的仿真分析，实现了载人运载火箭全要素约束迭代制导。

1 全要素约束迭代制导技术

1.1 基本原理

迭代制导是在最优控制原理基础上发展起来的，根据飞行器实时的位置、速度以及终端约束条件，以燃料消耗最少作为性能指标，将发动机推力矢量方向作为控制变量，用解析的方法计算出达到目标轨道所需的速度增量、位置增量，并依据极大值原理规划出最佳飞行程序角。

在轨道坐标系下的展开的运动方程为

式中,,,V,V,V分别为火箭位置和速度矢量在轨道坐标系三轴上的投影；˙为飞行实际过载；(),()分别为轨道坐标系中的俯仰和偏航角；g(),g(),g()为引力加速度在轨道坐标系中的3个分量。

全要素约束迭代制导是在迭代制导的基础上，对载人火箭的终端5个轨道根数和3个姿态角等全要素变量进行约束控制的制导技术。在未配置调姿系统的条件下，仅仅依靠对俯仰程序角、偏航程序角、滚转程序角和关机时间这4个量的控制，还无法进行全要素变量约束，必须进行控制参数扩充。原有的迭代制导控制参数只有4个，只能满足速度和位置约束，而无法满足姿态约束。因此增加程序角系数5和6，再增加2个变量进行姿态约束，具体思路如图1所示。

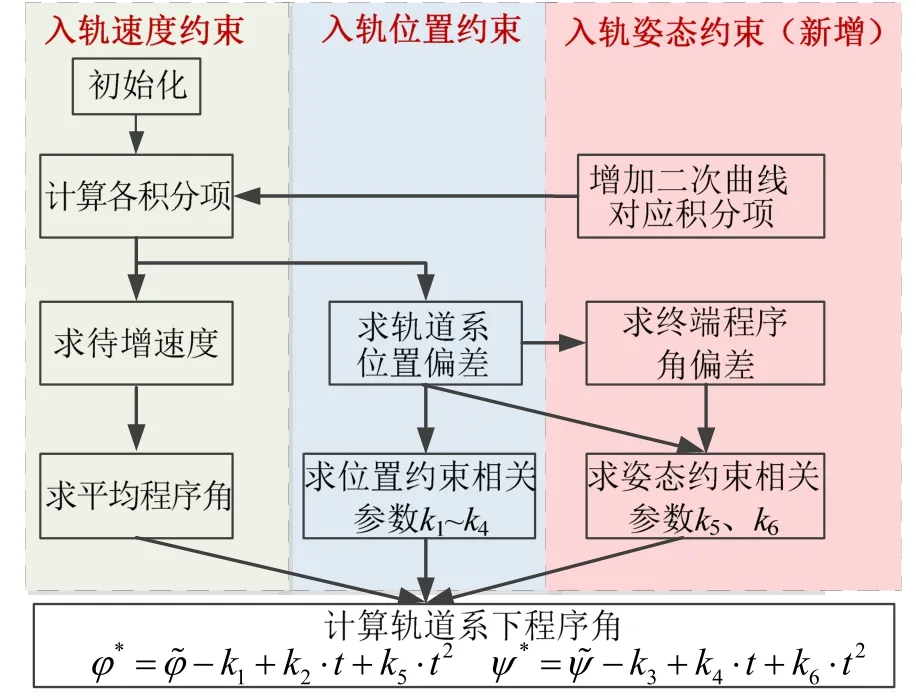
图1 全要素迭代制导原理Fig.1 Schematic Diagram of All-element Constrained IGM

中国载人运载火箭在进入真空段即接入迭代制导，迭代制导须考虑在主机段、游机段的接续迭代（见图2），若要同时满足在迭代制导末端时程序角和角速率的高精度要求，则需要在迭代末端进行常值约束，以确保载荷能以较小的角速率平稳进入近地轨道。

图2 载人运载火箭的全要素迭代制导程序角规划分段Fig.2 Angle Planning Segmentation of All-element IGM for Manned Launch Vehicle

俯仰程序角计算方程为

1.2 偏航俯仰约束

1.2.1 约束方程

迭代程序角要满足多个约束条件，约束方程的建立可通过对运动方程的展开形式进行积分得到。由于载人运载火箭的整个真空飞行段包括主机迭代段、游机迭代段和迭代末段，则分别在整个真空飞行段建立了偏航、俯仰通道的约束方程，具体如下：

a）姿态约束方程。

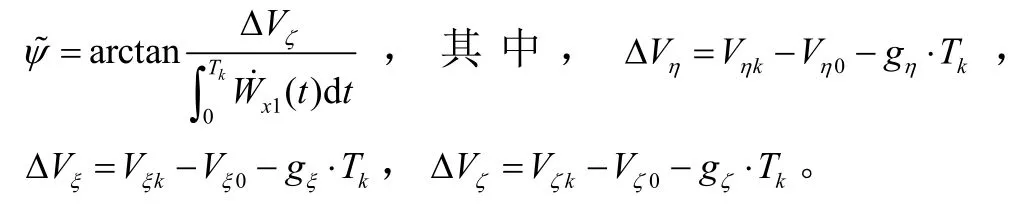
b）速度约束方程。

对式（1）进行积分可得到速度方程：

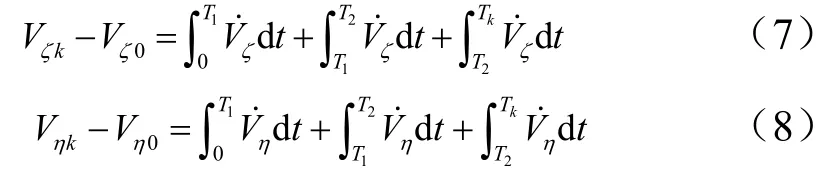
式中V,V为入轨时刻的速度矢量在轨道坐标系下的分量；V,V为当前时刻的速度矢量在轨道坐标系下的分量。

c）位置约束方程。

对速度约束方程进行积分，得到位置约束方程：

式中ζ,η为入轨时刻的位置矢量在轨道坐标系下的分量；,为当前时刻的位置矢量在轨道坐标系下的位置分量。

综上所述， 通过对上述6个约束方程的求解，可实时得到程序角系数16～，进而得到实时制导程序角用于控制。

1.2.2 方程求解

对于载人运载火箭，要求程序角变化平稳，以利于姿态的平稳控制，故满足位置和姿态约束的调节量相对于总调节量而言应占很小的部分，因此可做小角度近似假设。因此代入上述偏航通道的速度约束方程，通过小角度假设可简化得到如下方程：

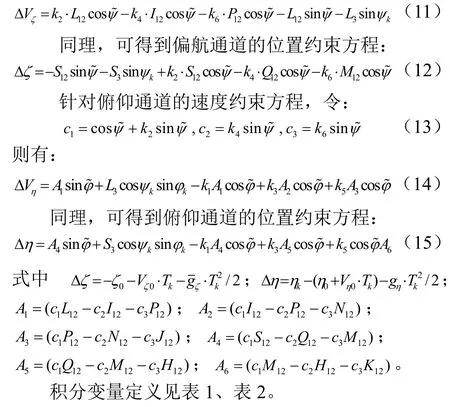
表1 单重积分变量定义Tab.1 Single Integral Variable Definition Table

表2 双重积分变量定义Tab.2 Double Integral Variable Definition Table

由上述公式可得到相应的俯仰和偏航程序角系数：

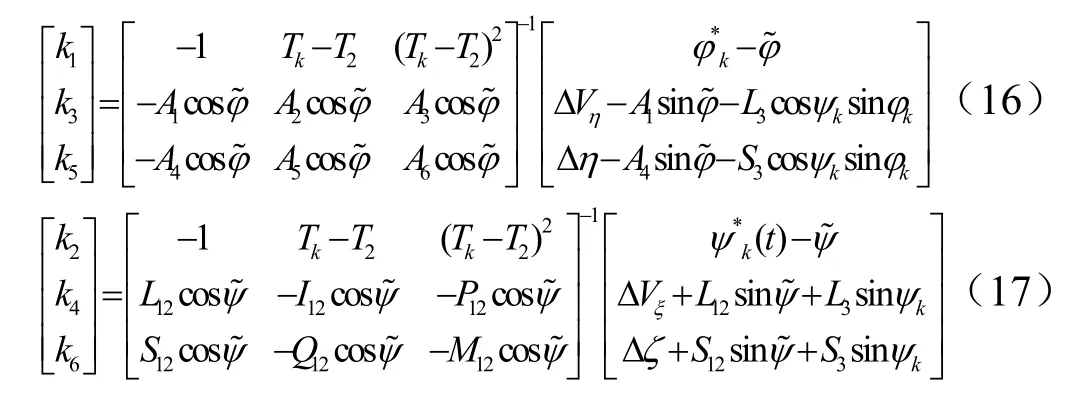
通过上述程序角系数～的实时求解，代入式（3）、式（4）即可得到轨道系下的迭代程序角，然后通过惯性系到轨道坐标系转换方程完成姿态约束角的坐标系转换后，得到的惯性系的迭代程序角才能参与制导方程进行控制。

1.3 其他要素约束

通过上述俯仰、偏航通道的速度、位置和姿态约束方程，可实现对4个轨道根数和2个姿态角的控制，要实现全终端要素约束，还需要对纵向通道的1个轨道根数和1个姿态角进行约束控制。

常使用关机量控制实现对纵向通道轨道根数的控制。载人运载火箭末级入轨的关机量是半长轴关机方程为

式中Δ为半长轴偏差；a为目标轨道的半长轴，是常数；为实时半长轴，=(2-)。

当Δ≥0时，表示可以实时关机。针对轴滚转通道的姿态控制，对于载人运载火箭而言，常用零值约束。

2 局限性分析及应对措施

载人运载火箭的典型特点是高可靠性，要求迭代程序角曲线变化平稳。

2.1 程序角平稳性分析

为了实现姿态约束，全要素约束迭代制导在原有的一次计算公式的基础上，增加了二次项，以俯仰程序角为例，其对应的程序角速率的变化率如下式所述：

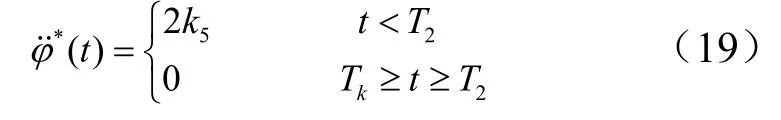
由式（19）可知：程序角速率的变化率只有在迭代末段才会等于0，在其他时间段，若不等于0，则存在程序角速率的波动。由于会受飞行过载的影响，因此相较于传统的迭代制导方法，全要素约束的迭代制导方法规划的迭代程序角对飞行过载信息更敏感。

因此，对载人运载火箭采取相应的措施以保持程序角的稳定性，具体如下：

a）程序角强滤波。

在迭代算法中，由惯性器件实时敏感到的飞行过载参数作为表征火箭瞬时推重比的性能参数，用于多项迭代参数的估算，而飞行过载参数容易受到发动机推力瞬时变化和惯组采样等因素的影响，会产生波动，因此需要对相关信息进行强滤波。图3给出了滤波前后的程序角。

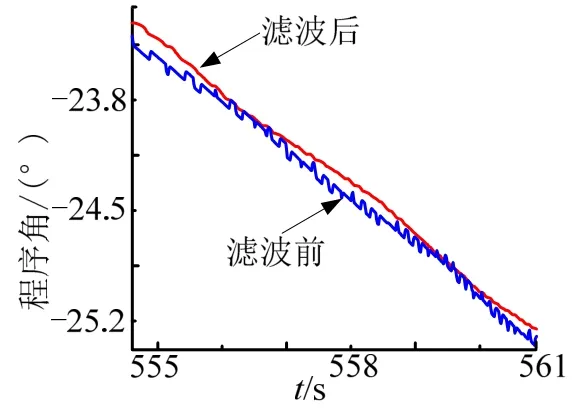
图3 滤波前后的程序角曲线Fig.3 Program Angle Curve Diagram before and after Filtering

由图3可知：通过强滤波后，能明显削弱程序角波动，提高迭代算法的平滑性，确保载人任务飞行过程平稳。

b）程序角角速度和角度限幅。

对输出的程序角进行角速度和角度限幅，可以提高火箭飞行稳定性，并且有助于提高故障情况下的安全性。但角度限幅同时带来的是对迭代制导能力的限制，载人火箭采用26°的角度限幅，也直接保证了26°以内的终端入轨程序角偏差精度。而对于全要素约束迭代制导算法已经对终端姿态进行了约束的情况，因此，在工程设计过程中，可考虑适当放宽迭代程序角的限幅角度，增加迭代制导能力。

c）接入迭代制导的时间前移。

将迭代制导的接入时间提前，有助于提高程序角的平稳性。针对某些干扰较大的情况，则会出现需要制导控制的时间延长，从而导致燃料消耗量变大。为了解决该燃料消耗问题和考虑精度的前提下，可将原设计接入迭代制导的时间提前。这既可以增加了系统对干扰的适应能力，也可以减少后续制导时间。由于迭代制导时间提前，此时积累的方法误差较小，需要规划的程序角与理论程序角差异也较小，这样也能保证迭代程序角在接入段的平稳过渡。

2.2 矩阵病态化分析

全要素约束迭代制导中采用了矩阵方式来计算程序角系数，但在某些异常情况下会出现病态化，导致矩阵不可逆，无法求解程序角系数。

因此对矩阵进行防止病态化的处理：

a）进行矩阵可逆值的判断，如不可逆，则保持上一拍程序角；

b）通过程序角限幅，防止异常程序角出现。

3 算 例

以载人火箭发射飞船为例开展六自由度（6DOF）数学仿真计算，首先对全要素约束迭代制导技术的姿态约束性能与传统迭代制导方法进行仿真对比分析；然后重点通过Monte Carlo模拟打靶仿真，对入轨时刻轨道根数及入轨姿态等全要素进行性能定量分析。

3.1 姿态约束性能仿真分析

仿真条件设置如下：

a）目标轨道为近地椭圆轨道，自200 s开始接入迭代制导，直至载荷入轨。

b）设定入轨俯仰姿态角为-30°，偏航姿态角为1°，滚转姿态角为0°。

c）干扰项偏差：结构质量偏差，燃料加注量偏差，发动机流量偏差，发动机比冲偏差，发动机后效冲量，推力线法向偏斜，质心法向横移，大气密度偏差和大气压力偏差等。

选取20项不同的误差组合进行6DOF仿真，2种迭代制导方法（迭代制导和全要素约束迭代制导）姿态角的仿真曲线如图4和图5所示。

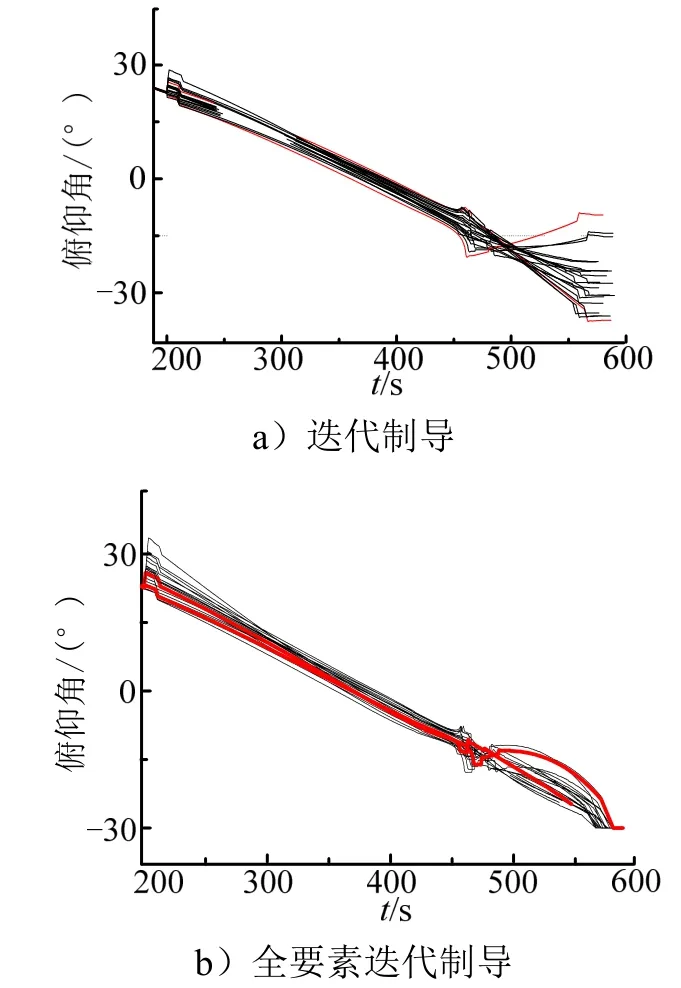
图4 俯仰角曲线Fig.4 Curve of Pitch Angle

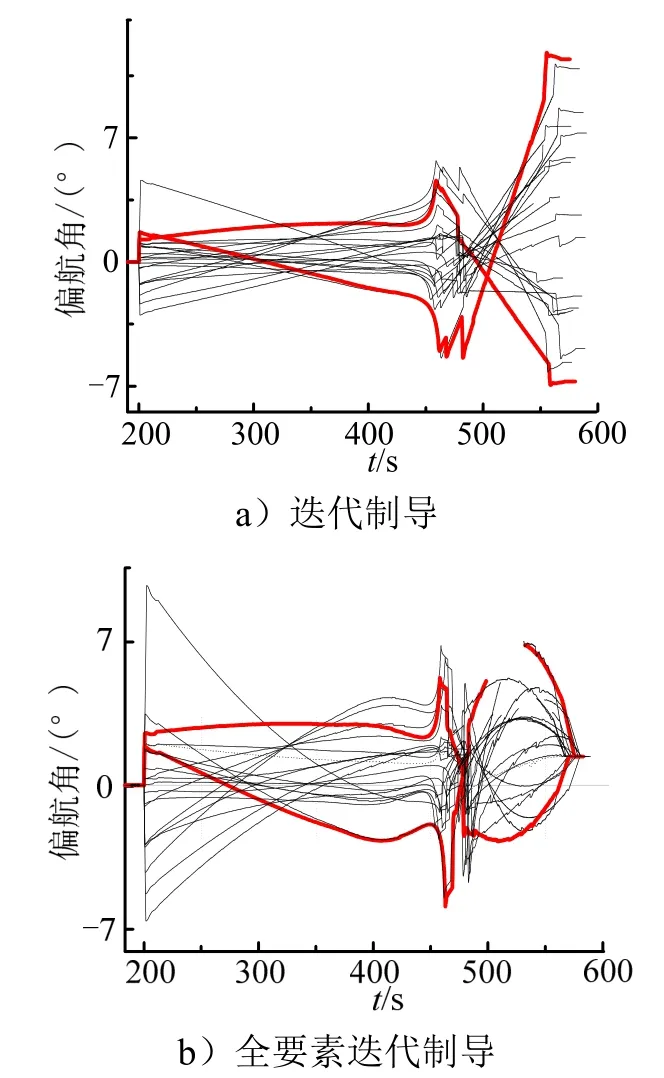
图5 偏航曲线Fig.5 Curve of Pitch Angle

由图4和图5可知：迭代制导方法无法对俯仰偏航通道的入轨姿态角进行约束，而全要素约束迭代制导方法可对俯仰姿态角、偏航姿态角分别进行-30°和0°的终端的姿态角约束的效果相对于迭代制导方法而言更好。

3.2 Monte Carlo模拟打靶仿真分析

将不同的干扰项偏差随机添加进入仿真系统进行Monte Carlo模拟打靶仿真，其参数偏差的概率模型均为正态分布模型(,)。

模拟打靶仿真数量设为5000条，则各个终端要素的偏差打靶结果如图6、图7所示。各个靶点图中，采用各轨道根数的偏差值占工程任务总体指标要求的百分比来评估入轨精度，采用各姿态角角度偏差来评估入轨姿态。 入轨姿态角偏差的打靶结果如图8所示。

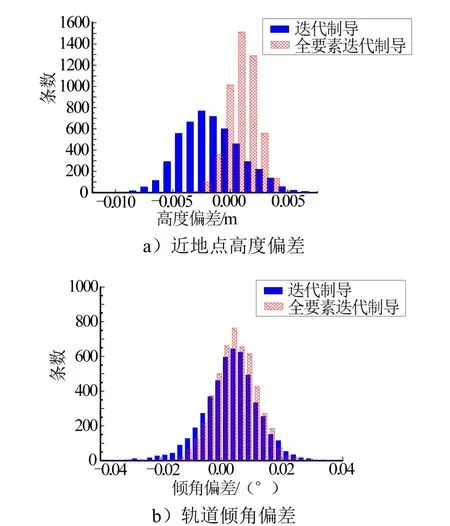
图6 近地点高度偏差Δhp与轨道倾角偏差Δi的直方图Fig.6 Histogram of Perigee Height DeviationΔhp and Orbital Inclination Deviation Δi

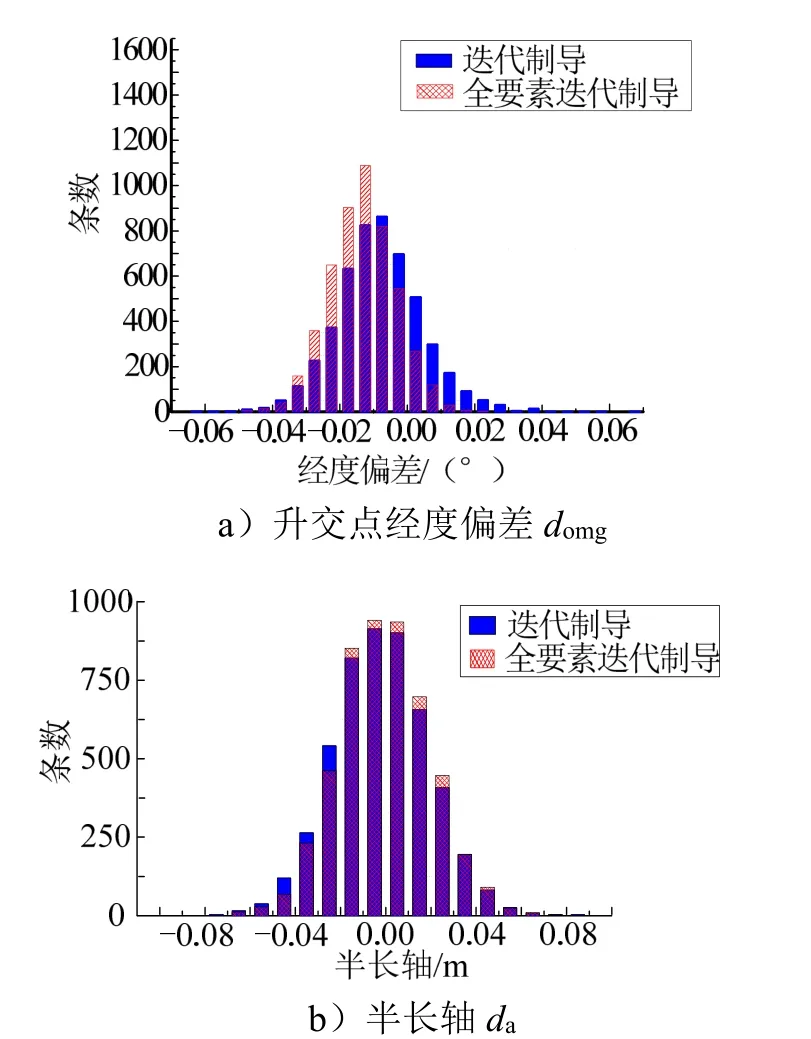
图7 升交点经度偏差domg与半长轴da的直方图Fig.7 Histogram of Ascending Node Longitude Deviation domg and Semi-major Axis da

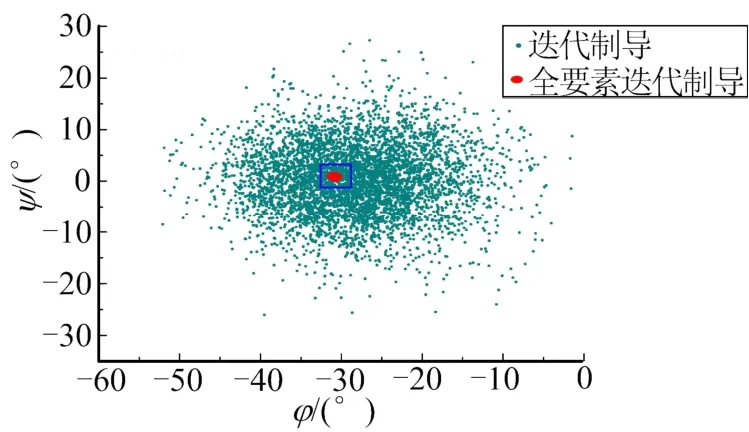
图8 姿态角偏差,φψΔΔ的靶点Fig.8 Target Point Diagram of Attitude Angle Deviation

由上述各图可知：升交点经度、轨道倾角、近地点高度与半长轴等轨道根数偏差值均在指标要求的10%以内；入轨姿态角偏差均在0.7°以内。

为更好评估采用全要素约束迭代制导技术的入轨精度，与迭代制导方法进行对比，结果见表3、表4。

表3 入轨精度百分比值Tab.3 Percentage Value of In-orbit Accuracy

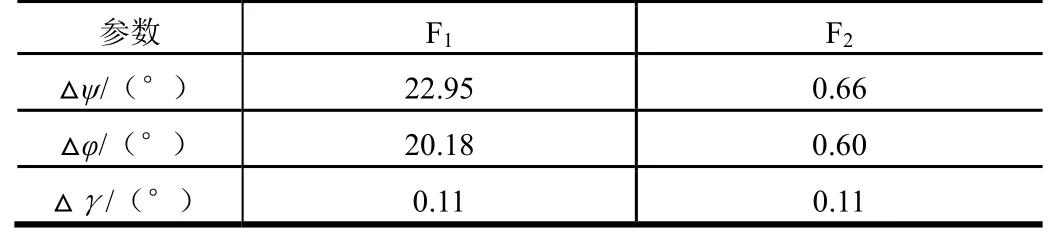
表4 入轨姿态精度Tab.4 Terminal Attitude Accuracy

由表3、表4可知：全要素迭代制导（F2）相对于迭代制导（F1）而言，入轨精度未降低，入轨姿态精度却提高了近两个数量级。

4 结 论

本文针对传统迭代制导无法约束入轨姿态的不足，提出了一种应用于载人运载火箭的全要素约束迭代制导技术，通过优化终端姿态反馈算法并精细化考虑迭代末段的速度和位置约束量，使得载人运载火箭实现了以期望姿态角实现高精度入轨。算例结果表明，该方法相较于传统迭代算法，可以实现高精度的入轨时刻姿态约束，入轨精度满足总体要求，可以满足后续发射任务需求，具有重要的工程应用价值。