一种箭体多级联合全自动垂调控制算法研究及系统设计

刘丽媛，邢 然，王赵帅，郑国昆，刘海波

（北京航天发射技术研究所，北京，100076）

0 引 言

火箭垂直度调整的目的是调整发动机推力线，从而减小火箭起飞段的横向漂移量。垂直度调整是非常重要的一个环节，其可靠性及精度是系统重点关注指标。

运载火箭通过发射平台支承臂机械接口竖立在发射平台上，中国运载火箭除新一代大型运载火箭外，均为4个支承臂支承运载火箭箭体的支承方式，故称为“四点支承”。支承臂是发射平台的部组件之一，通过液压动力驱动支承臂可实现支承臂的伸缩运动，运载火箭采用四点支承时，通过对4个支承臂的协调动作，即可实现运载火箭的垂直度调整操作。

现有的基于4点支承的垂直度调整方法，多为半自动或单级垂调控制模式。为满足载人火箭的高可靠及高精度需求，需设计一种基于全自动多级联合的高精度垂调控制策略的控制系统，将各级水平度控制在相应的允许范围，实现整体箭体垂直度调整需求。这就要求控制算法需能够解决各级间的反向作用及相互影响，以满足系统在性能优化的基础上，减少垂直度调整时间的总体要求。

本文对多级整体垂调需求进行解析，通过理论分析，建立算法模型及系统，并结合试验数据，对全自动多级联合的影响因素及控制算法进行探讨与改进，最终实现4点平面下的快速调平控制。

1 系统需求及原理模型

1.1 系统需求

本系统及算法需求就是建立在4点支承的基础上的多级联合全自动垂调系统，既适用于I级火箭与发射平台对接后的独立垂调，也适用于Ⅱ级火箭、星箭组合体上箭对接后的I、Ⅱ级同时垂调。

本系统应根据I、Ⅱ级水平仪数据，将测量垂直度与目标垂直度偏差值调整到总体要求范围内，并在过程中保证满足如下条件：

a）支承臂高度升降范围为0～120 mm，其中两端各留10 mm的安全范围。当支承臂升降过程中达到10 mm的上下限范围时系统进行报警及校正；

b）4个支承臂在垂直度调整过程中执行升降动作。动作时，当高差Δ绝对值不小于2 mm时进行报警、校正。

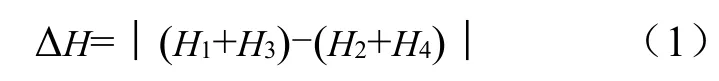
式中～分别为Ⅰ～Ⅳ支承臂高度传感器示值，单位mm；

c）I级火箭转场后进行单独垂调，要求I级水平度（以下简称）满足∣∣≤0.5′；

d）II级火箭、星箭组合体转场后对II级进行垂调，要求I、II级水平度（以下简称）分别满足∣∣≤3′,∣∣≤15′。

调整到位后，全自动垂调自动停止，并给出调整完毕的结论。

1.2 原理模型

四点支承调平，将由4个独立象限中支承臂所在点位确定为1、2、3、4四点的平面，记为一级平面,如图1所示。

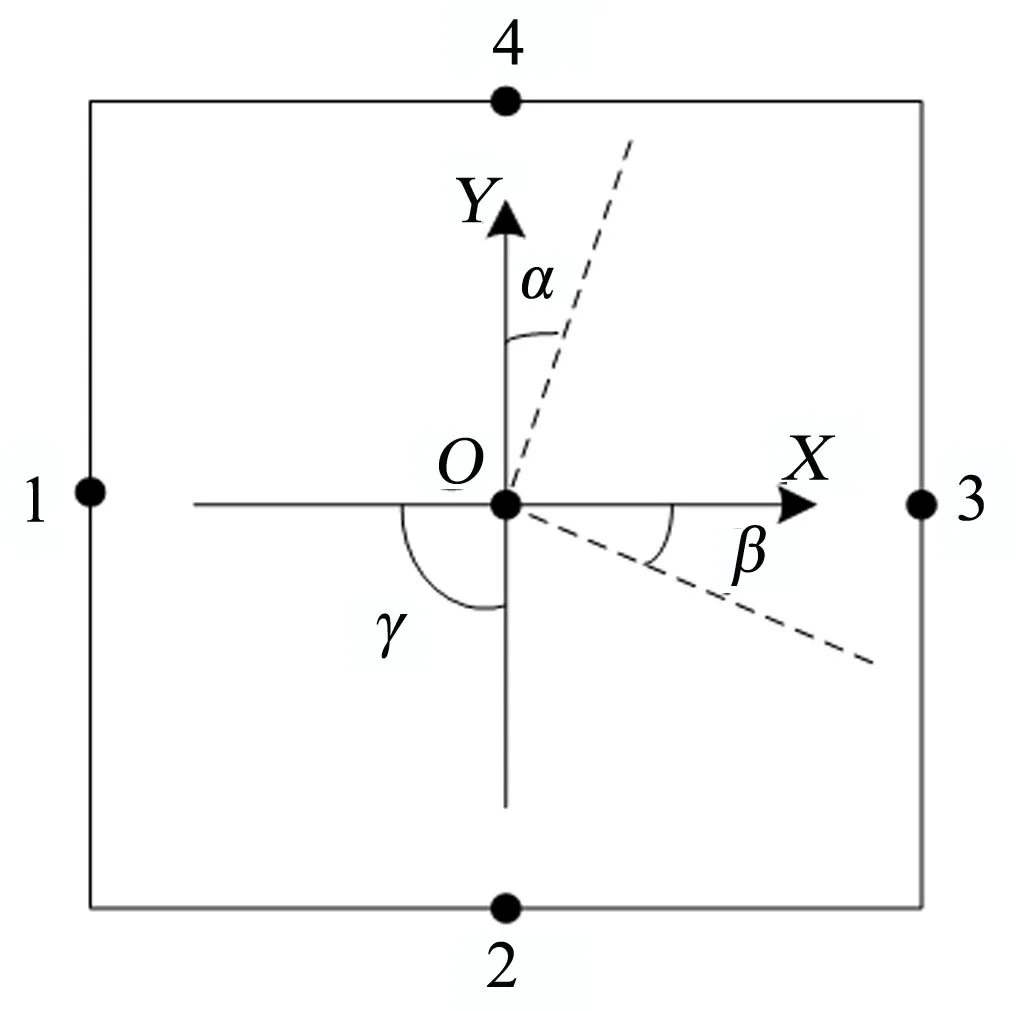
图1 一级平面模型Fig.1 Level 1 Plane Model Diagram

水平传感器沿、方向布置，、两个方向的水平倾角分别为和，两传感器间的夹角为，则平台的倾斜角度可由和合成为

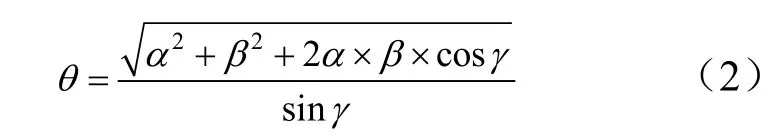
I、Ⅱ级水平数据原理均可简化为如上模型，但I、Ⅱ级测量的水平数据，受4个支承臂动作调整的影响不同，在多级联合的情况下，4个支承点的动作对平面的作用效果存在差异。需通过合理的算法模型进行解算，达到多级的综合优化调整效果。

2 多级联合垂调控制算法研究

2.1 控制影响因素解析

通过系统需求分析及控制原理解析，不难发现多级联合垂调控制算法应能实现同步运动误差、水平度范围多因素相互作用下的最优动作“路线”规划。

2.1.1 同步运动误差控制

为使4点支承下的各级箭体水平面处于各自的同一水平面上，在支承臂上升、下降过程中每一时刻都要保证4路升降的位移变化绝对值基本相同，因此不仅要对每一路升降支承臂的位置进行精确位置跟踪控制，还要对多路升降支承臂进行高精度同步控制，即不仅要考虑每路位移实际值与设定值之间的跟踪误差，还需考虑该路与相邻一路之间位移的同步误差。针对系统被控对象多的特点，基于耦合补偿原理，本研究采用环形耦合控制方式对多路液压马达进行同步控制，对于每路液压马达，仅考虑与其相邻一侧液压马达的位移偏差，该位移偏差反馈到该路支承臂，对其控制量进行补偿修正，各路支承臂之间两两耦合，形成耦合环，在负载扰动等情况下，仍能保证各路之间较好的同步控制精度。位置闭环跟踪控制模型如图2所示。

图2 位置闭环跟踪控制模型Fig.2 Postion Closed-loop Tracking Control Model Diagram

由个支承臂构成的多点控制系统，第点的跟踪误差可定义为

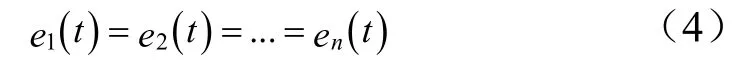
为了更好地反映各点位置误差的变化情况，按邻近次序定义同步误差为ε()如式（5）：

2.1.2 水平度调整控制

不同级平面的测量角度传感器不同，但控制模型一致。针对每一独立级平面，系统需求以该级水平度为判据，可采用角度调平方法。该方法实质是对水平仪检测实际倾角角度和进行调整，直到检测到的两个角度满足测量垂直度与目标垂直度偏差值小于10″的误差范围内，则平台实现调平。

常见的角度误差控制调平法的控制逻辑如图3所示。假设最高点不动，分析角度控制误差调平方法。当＞0，＞0时，第1条支腿为最高点，保持第1条支腿的支撑点不动，则第2、3条支腿同时上升就会使减小，当减小至允许误差范围值时2、3支腿停止上升；接下来令第3、4条支腿上升，从而使减小，当减小至允许误差范围值时3、4支腿停止上升，则平台实现调平。对于两个倾角、的调节，一般先调节较大的角度，注意在调节过程中，务必使最高点保持不动。

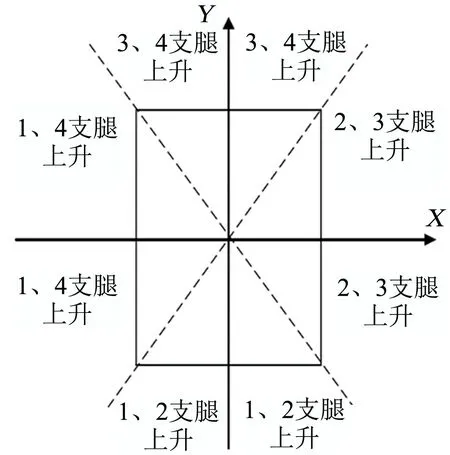
图3 水平度控制模型Fig.3 Levelness Control Model Diagram

但由于受箭体特性影响，在本系统角度控制调节时无法保持最高点不动原则。所以调整角度控制策略如下：

其中，项倾角为1、3支承臂连线角度，正值为1低3高，项倾角为2、4支承臂连线角度，正值为2低4高。当︱︱＞0，︱︱＞0 时，对于两个倾角、的调节，先调节较大的角度。例如倾角较大，则先调节倾角轴线上的两个支承臂的高度，动作方向应为倾角变小的趋势一致，两个支承臂作反向运动，直到角度值满足调平要求，即可停止动作。反之亦然。

2.2 控制算法研究

通过各影响因素解析及控制模型建立，综合多级联合垂调的支承臂控制策略如下：

在支承臂控制过程中，系统实时采集各支承臂高度，计算控制误差，并将采集和控制输出信号传送执行机构及显示器，实时监测动作过程数据。同时接受来自I级火箭水平仪I-III象限垂直度、I级火箭水平仪II-IV象限垂直度、II级火箭水平仪I-III象限垂直度、II级火箭水平仪II-IV象限垂直度，用于支承臂垂调流程控制。

依据要求I级水平度、II级水平度，分别满足 ∣∣≤3′和∣∣≤15′，∣－∣≤18′自动调整；∣－∣＞18′协商手动调整。分解判断策略如表5所示，设为0′至1′之间的一个控制公差（默认0.5′）。其中，边界范围值及公差值均可根据要求进行设置调整。

表1 垂调控制策略分析表Tab.1 Vertical Control Strategy Analysis Table

由于算法采用水平度及位移值双闭环处理，为避免产生反复调节及“过矫”情况，同时在算法控制中，设定控制原则如下：

a）设定优先级分别为：水平度→位移值；

b）各倾角方向单独判断调整，确定各倾角线上支承臂动作；

c）单次动作中，单一倾角方向上的支承臂动作调节，需按首次判定方向动作，不允许进行反向调节。

3 控制系统设计

本文设计的控制算法，搭载支承臂垂调控制系统设备进行验证。系统硬件设计架构见图4，系统采用PLC控制器，运行周期10 ms左右，具有快速的计算性能。控制器通过模拟量采集通路采集各支承臂的位移传感器的实时数据值，通过串口接收箭上各级水平角度数值，通过控制器控制算法计算判断，给出各个支承臂的动作控制信号，从而驱动执行机构进行动作，达到调整箭体整体垂直度的效果。其中，执行机构包括支承臂、液压驱动系统等外围所有动作设备。控制系统主要通过输出不同的流量控制信号，给比例放大板，控制液压系统比例流量阀的调节，驱动液压马达，从而实现支承臂的动作精度控制。

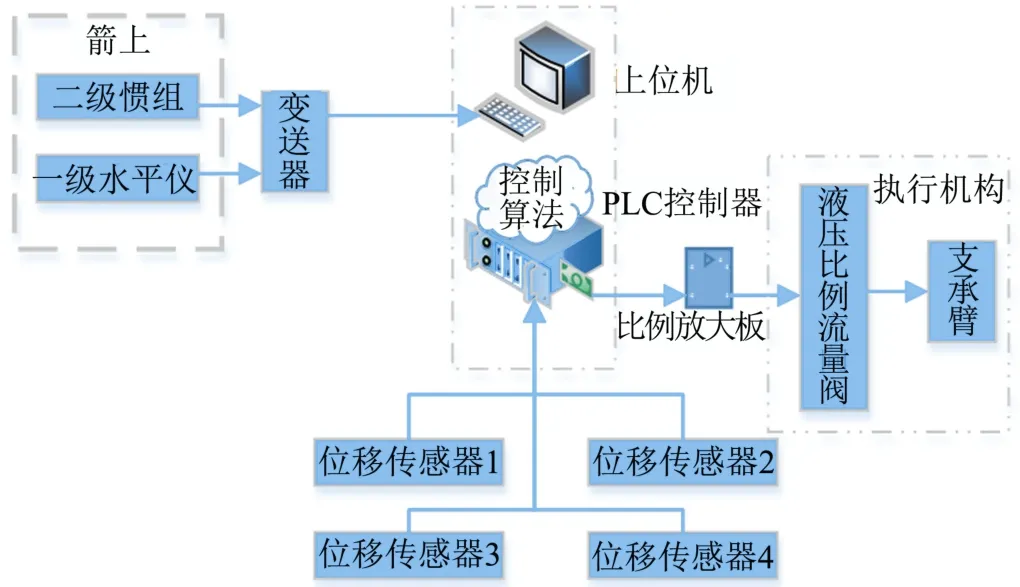
图4 控制系统架构Fig.4 Control System Architecture Diagram

4 试验测试数据及结果分析

4.1 试验测试数据

基于支承臂垂调控制系统设备对控制算法进行了两部分验证测试。

4.1.1 边界范围控制测试

主要以水平仪的各种边界情况进行策略判定测试验证在极端工况下的算法自适应情况。当I、II级水平仪数据在要求范围内时，不进行调平动作；当不满足要求时，共有3种工况：

a）I级水平仪满足，II级水平仪不满足。

此情况下的水平角度边界测试值及动作状态值如表2所示，其中，分别为1，3方向和2，4方向上的倾角值，下角标1，2代表所相应的级层。

表2 水平角度及动作状态1Tab.2 Horizontal Angle and Motion State 1

b）I级水平仪不满足，II级水平仪满足。

此情况下的水平角度边界测试值及动作状态值如表3所示。

表3 水平角度及动作状态2Tab.3 Horizontal Angle and Motion State 2

c）I、II级水平仪都不满足。

此情况下的水平角度边界测试值及动作状态值如表4所示。

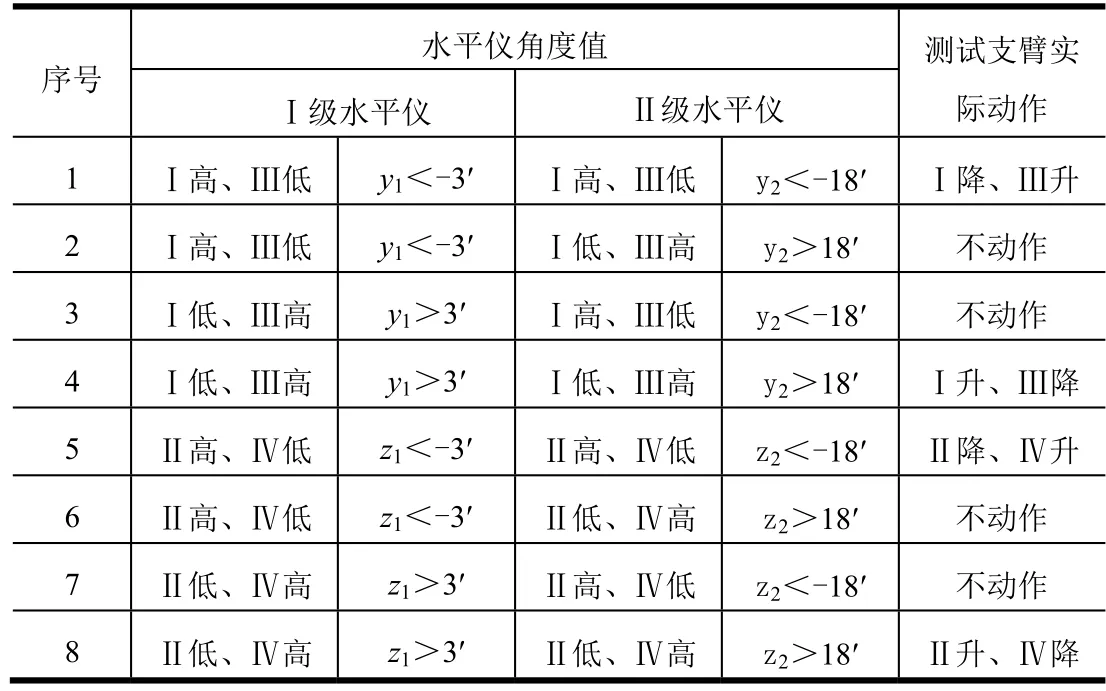
表4 水平角度及动作状态3Tab.4 Horizontal Angle and Motion State 3

根据控制系统实物测试边界结果可见，控制算法在各边界工况下的自动判断优化选择有效，与期望运动控制效果一致，能够满足系统自动多级联合垂调判断控制使用要求。

4.1.2 控制性能测试

测试控制算法在任意工况下，调节动作的控制性能及效果。以实际测试时某次动作数据为例，水平角度数值向倾角5′08″，向倾角4′09″，各支承臂初始动作高度值均为60 mm，目标值向倾角2′，向倾角2′。调整后，水平角度数值向倾角2′04″，向倾角2′04″，各支承臂高度值依次为Ⅰ：58.39 mm，Ⅱ： 59.35 mm，Ⅲ：62.06 mm，Ⅳ：61.20 mm。各支承臂位移变化趋势如图5所示，水平角度变化趋势如图6所示，倾角角度值在实际计算及记录中统一转换为单位秒。

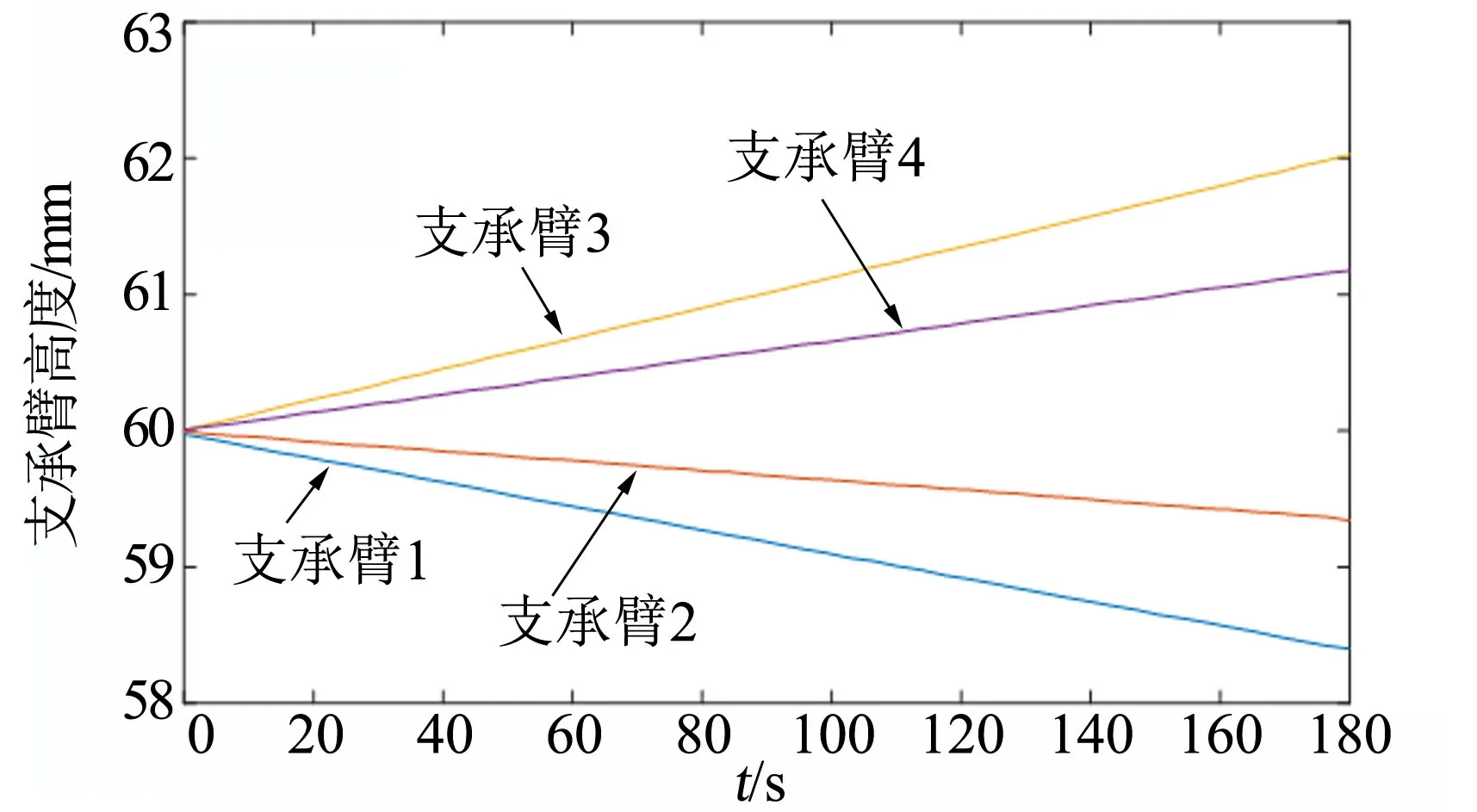
图5 支承臂位移变化趋势Fig.5 Displacement Trend Diagram of Supporting Arm

图6 水平角度变化趋势Fig.6 Horizontal Angle Trend Chart

4.2 结果分析

结合试验数据分析，可总结多级自动垂调控制算法下支承臂动作规律如下：

a）各支承臂动作时，对关键因素的影响由大到小为：水平度→位移值。

b）水平度调整时，不同向倾角间，相互影响较小，变化趋势趋近一致。

c）垂直度调整时高度值及变化差值算法能够闭环控制在±0.5 mm。

试验结果表明，本文设计的控制算法能满足多级联合垂调控制的需求，控制精度高，提升了垂调控制性能及控制时间，具有极强的工程应用性。

5 结 论

本文依据需求，以水平倾角及支承臂位移高度作为调整控制对象，设计了一种多级联合垂调控制算法，试验证明该算法能高效实现箭体垂直度的快速判定与调整控制，调整结果与目标期望值一致，将误差控制在要求范围之内，实现高精度双闭环垂调控制功能。基于设计方案的试验结果，对垂调控制下的各关键因素的调整趋势及规律做了深入探讨，总结了各关键因素受控制策略影响的优先程度，实现了全自动多级联合的高精度垂调控制。该控制算法已应用于某型号活动发射平台大修的电气系统更新研制中，并经过了出厂测试、靶场现场安装调试及发射任务的考核。