一种基于 ARIMA 模型与 3 σ 准则的取水异常检测方法

赵和松 ，王圆圆 ，孙爱民

（1.水利部信息中心，北京 100053；（2.北京金水信息技术发展有限公司，北京 100053；（3.河海大学计算机与信息学院，江苏 南京 211100）

0 引言

截至 2021 年 1 月统计的国家水资源监控能力建设项目一期建设水资源取用水监测点约为 17 000 个，每年产生近 1.5 亿条监测记录，这些监测值存在超出预设极值等异常现象，也存在缺报漏报情况。随着取水点的不断增加、取水设备的不断改进和取水周期的不断缩小，判断这些异常值和预设极值的难度越来越大，同时也加大了对今后取用水的规划难度。异常值[1]是指偏离于大部分数据集的数据，产生这部分数据的原因有很多，因此需要对其进行异常检测，找出原因。

目前对于检测数据的异常判别种类比较单一，主要是基于有限的业务规则和传统统计学的人工判别方法。人工判别方法先通过日取水量数据的业务逻辑规则进行数据清洗和预处理，再通过统计学的方法判断数据是否异常。这种方法需要消耗大量的人力、时间和财力，而且处理效率低下，不能及时检测出异常数据，也不能对异常数据给出合理的参考修正值。

近年来，随着机器学习在数据挖掘、自然语言处理和语音识别等领域的快速发展，取用水异常分析成为机器学习的一种应用领域，相比传统的统计方法和简单的规则，取用水异常分析技术能够更好地识别偏离分布规律等的复杂异常。通过对水资源取用水监测数据进行横向和纵向分析，深度挖掘规律，取用水异常分析技术可精准识别异常值。对于简单的异常，则在数据清洗过程中设置规则直接过滤。因此，取用水异常分析技术能明显提高取用水数据采集的整体和数据等质量评价工作的效率。

异常检测也称为异常挖掘[2]，即从数据集中找出异常值。异常值可以分为单变量和多变量异常值。当查看单个特征空间中的值分布时，可以找到单变量异常值；多变量异常值可以在n维空间中找到。

异常值检测有很多方法，主要包括：

1）基于 k-means 算法的异常检测。k-means 算法[3]是无监督的聚类算法，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇，将不属于簇内的点判定为异常点。k-means 算法过度依赖簇的选取，因此正确率和效率都不高。

2）基于距离的异常值检测。这种检测方法规定如果 1 个数据点的周围没有其他的点，可认为这是1 个异常点。Ngo 等[4]提出针对时间序列可变长度的异常检测算法，该方法的时间复杂度小，但对于局部存在的异常点，检测效果不佳。

3）基于密度的异常值检测[5]。该检测方法通过研究对象及其相邻对象的密度进行异常检测，但需要将对象周围的密度与其局部周围的密度进行比较，因此需要较高的时间复杂度。

4）基于时间序列数据的异常值检测模型方法。牛丽肖等[6]提出一种基于小波变换和差分整合移动平均自回归模型（ARIMA）[7]的短期电价混合预测模型，该模型能够很好地检测出突变点，但对时间序列的非线性部分检测仍然存在不足。单伟等[8]采用自相关和偏自相关系数的拖尾建立 AIRMA 模型，并用于预测和异常检测，这种方法是假定数据集符合所用的模型，存在着很大的局限性。孙建树等[9]提出基于 ARIMA-SVM 的水文时间序列异常值检测方法，该方法能很好地处理线性部分的数据，同时使用支持向量回归（SVR），但可能导致异常值不能被完全检测出来。丁小欧等[10]提出基于相关性的异常检测算法，实现对复杂模式的异常数据精准识别，但对于有限标签的弱监督异常检测方法需要进一步改进。任勋益等[11]提出一种基于向量机和主元分析的异常检测，在异常数据较多时，检测效果并不好。温粉莲[12]利用K均值聚类算法对历史数据进行划分，同时利用曲线拟合和 ARIMA 得出数据中的异常值，能够较好地发现异常数据。胡珉等[13]总结现有多维时间序列异常算法，提出异常检测的研究难点和趋势。

基于上述内容，本研究基于 ARIMA 对用水异常值进行检测，使用高斯分布的 3σ准则判断日取水量中的异常值，并通过时间序列分解算法 STL[14]判断异常值附近的取水量趋势。

1 取水异常检测预备知识

1.1 ARIMA 模型

ARIMA 模型中，AR 是自回归，MA 为滑动平均。模型的基本思想是用现有的平稳时间序列数据去预测将来的值，即通过现有的稳定时间序列数据求出未来的数据。ARIMA 模型表示为式中：p为预测模型中采用的时间序列数据本身的滞后数；q为预测模型中采用的预测误差的滞后数：Фi为自回归参数；θi为移动平均的参数；εt为误差项，通常是独立的；Xt为时间序列数据；d为时间序列数据需要进行差分的次数，d∈Z，d ＞0；L为滞后算子。

本研究构建 ARIMA 模型的步骤如下：

1）对时间序列数据进行预处理和清洗。

2）对时间序列数据进行平稳性处理，如果数据为平稳性数据，则进入下一步，如果日取水量数据为非平稳性数据，则通过差分的方法进行处理，直到该数据为平稳性数据，同时差分的次数为模型参数d的值。

3）确定 ARIMA 模型中参数p，q的值，将数据输入自相关和偏相关函数可以得到p和q的取值范围，从而找出最优的参数p和q。

4）确定 ARIMA 模型的拟合函数，通过函数可以确定该时间序列的整体走势。

1.2 3 σ 准则

若随机变量X服从 1 个位置参数为μ（均值）、尺度参数为σ（标准偏差）的概率分布，且其概率密度函数为

则这个随机变量为正态随机变量，正态随机变量服从正态分布，即高斯分布，记作X～N（μ，σ2）（N为样本数），其概率密度函数图像如图1 所示。

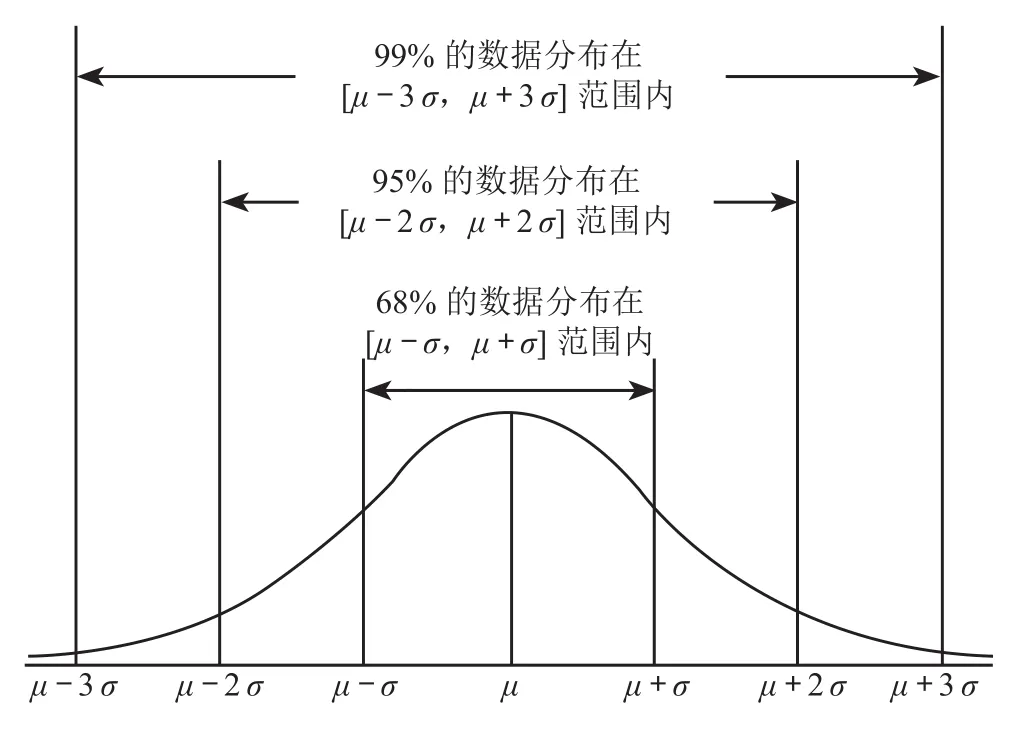
图1 高斯分布概率函数曲线图

3σ准则是先假设 1 组检测数据只含有随机误差，对其进行计算处理得到σ和μ，确定 1 个区间（μ- 3σ，μ+ 3σ），该组数据在（μ- 3σ，μ+ 3σ）区间的概率为 99%，即可将超过这个区间的值判定为异常值。

1.3 STL 算法

STL 为时间序列分解中一种常见的算法，将时间序列的某一时刻数据Yi分解成趋势分量Yt、周期分量Ys和余项Yr，即：

式中：i的取值为所有大于 0 的正整数，且该模型为加法模型，分解的分量互不影响。

本研究通过 STL 分解时间序列数据，观察时间序列数据的走势。

2 取水异常检测方法

取水异常检测方法主要分为数据的收集和预处理、模型参数的确定及实验结果分析等 3 个部分，取水异常检测模型建立的流程图如图2 所示。

图2 取水异常检测方法建立过程

2.1 数据预处理

本研究的数据分为两部分：第一部分数据是来自带有异常标签的时间序列数据，用于对实验模型的检验，且该部分数据不需要进行预处理；第二部分数据是水利部门收集的全国 15 000 个取水点的1.5 亿条取水数据，需进行预处理及缺失数据的填充。数据预处理及填充规则如下：

1）清洗取水量小于 0 的日取水量的值，使用该日前后 3 d 的平均值代替；

2）清洗取水量为空的值，使用该日前后 3 d 的平均值代替；

3）清洗取水量为 NA（无值）的值，使用该日前后 3 d 的平均值代替；

4）清洗日取水量为重复出现的值，直接将重复值删去；

5）清洗小时取水量数据出现日期推后的数据；

6）清洗当天的小时取水量累计值与当天日取水量不符的值，并用当天的小时取水量累计值作为日取水量数据；

7）小时取水量重复出现超过一定次数需要根据预处理结果进行优化，现阶段根据七点控制原则，拟定为连续出现大于等于 7 次需要优化；

8）以同种类型的用水户对应的正常取用水量数据为分析依据，清洗数据与正常取用水量不符合的日取水量数据（用例本身被其他的条件所覆盖）。

预处理后的数据需进行平稳性判断，通常采用单位根检验法判断。如果数据为平稳性数据则不做处理，否则对时间序列数据做差分处理，每次差分后都要进行平稳性判断，直到最后的数据具有平稳性，同时记录差分次数。

2.2 模型参数确定

ARIMA 模型中有参数p，d，q，对第一部分数据进行平稳性处理时记录的差分次数即模型参数d的值，通过自相关和偏相关函数图像中曲线与置信区间的交点求出参数p和q的值。

确定 ARIMA 模型参数的值，则可以拟合出时间序列数据趋势图，使用 3σ准则判断原始数据与拟合数据残差，如果残差在区间（μ-3σ，μ+ 3σ），则判定为正常值，否则为异常值。

使用 STL 算法可以得到该时间序列的点在时间上的分布走势，如果 2 个离得很近的异常值在该时间区间上存在上升或下降的趋势，则可以判断该区间上所有的时间序列的点为异常点，这样可以很好地弥补漏判的情况。

2.3 结果分析

通过异常值及拟合曲线能够判断模型的准确程度，若拟合较好，则说明模型可以对异常值提供较好的参考修正值，且通过异常值的判断可分析取水点产生异常数据的原因。

3 取水异常检测实验

为验证基于 ARIMA 模型与 3σ准则的取水异常检测方法的有效性，说明本研究提出的模型可以对异常值提供较好的参考修正值，且通过异常值的判断可分析取水点产生异常数据的原因，取两部分数据中具有代表性取水点的数据用于实验数据分析，研究提出的方法在数据中的表现。

本研究实验环境具体如下：CPU 为 Inter Corei5-7500，内存为 4 GB，操作系统为 Ubuntu18.04，软件使用 MySQL，Python，研究模型在 Pycharm 平台上开发并调试。

3.1 实验一

取 6 组来自雅虎带标签的时间序列的数据，选取其中具有代表性的数据，具体过程分析如下：

1）对 6 组数据进行平稳性检测，即 ADF 检测（单位根检验），变量为数据中自带的标签，计算得到的平稳性数据参数值如表1 所示，表中：K为延迟的具体数值；T为统计量；P为统计量对应的概率值；C1，C2，C3分别为 3 个置信度（1%，5%，10%）的临界统计值。

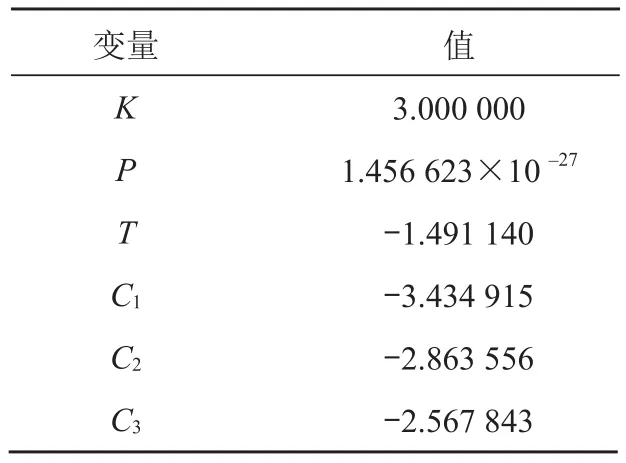
表1 平稳性数据参数及值

2）对带有异常标签的雅虎的数据集进行平稳性检测，可以得到统计量的值显著小于 3 个置信度（1%，5%，10%）的临界统计值，所以该组数据是平稳性时间序列数据。

得到的自相关和偏相关函数图像分别如图3 和4 所示，其中，水平虚线是为了在特定的函数相关性取值时取相关系数的值。这 2 个图说明：通过自相关和偏相关函数图像可以求出自相关系数p的值可能为 351 或 352，偏相关函数系数q的值可能为 5 或 6。通过对参数p，d，q的组合，可以得到ARIMA模型的最佳参数组合为（352，0，5）。

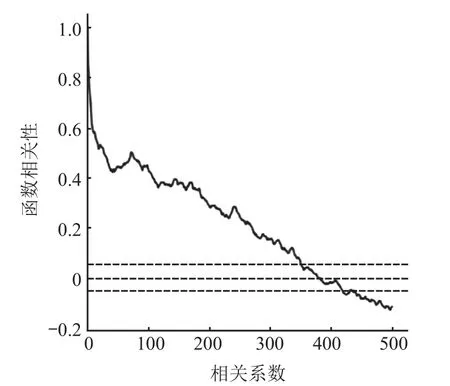
图3 自相关函数图像

图4 偏相关函数图像

3）通过 ARIMA 模型中的拟合函数求出该时间序列的拟合趋势，得到的时间序列数据拟合曲线如图5 所示。从图5 可以看出预测值和真值能够较好地拟合在一起，说明 ARIMA 模型效果较好。然后通过拟合曲线中的拟合值和原始值作差得到残差，最后通过 3σ准则判断残差是否在区间（μ-3σ，μ+3σ），即可以求出异常值。

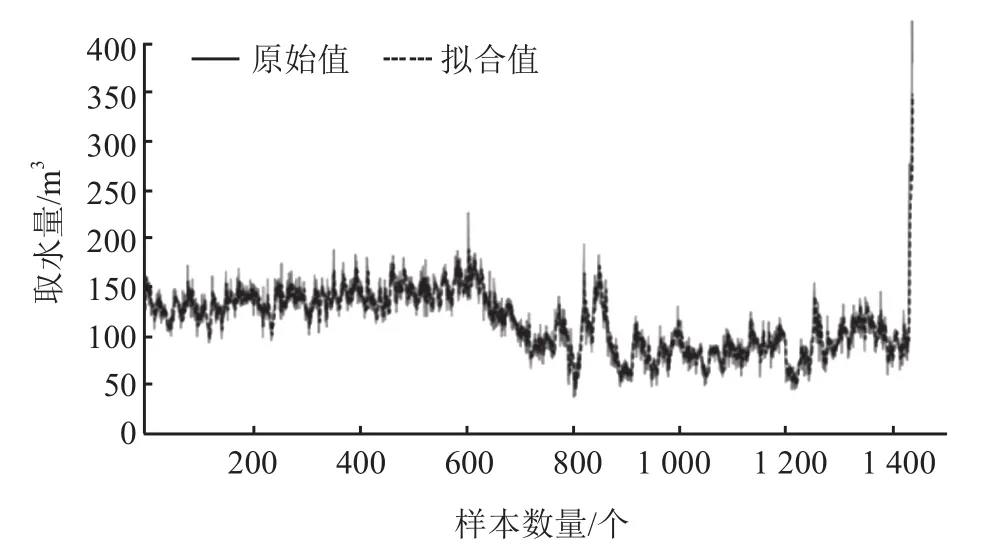
图5 时间序列数据拟合曲线

4）通过 STL 算法将时间序列数据分解为趋势分量Yt、周期分量Ys和余项Yr，分解的结果图如图6所示。

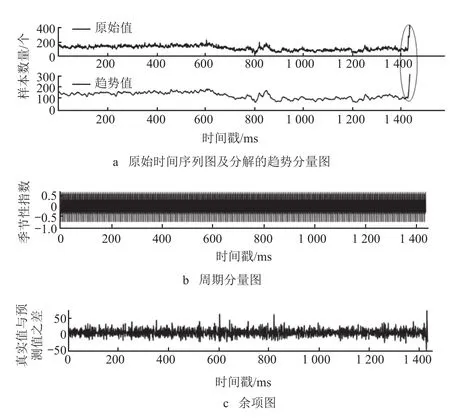
图6 STL 分解图

图 a 中，可以通过观察 2 个离得很近的异常值在该时间区间存在的趋势，判断该区间上所有的时间序列是否有异常点；图 b 可看出数据潜在的周期性；图 c 可看出当有非平缓趋势被检测到，原始数据去除周期、趋势后，残差项将增加一段陡坡。

5）使用 ARIMA 模型、3σ准则及时间序列分解算法进行分析，定义TPR为真正类率，又叫真阳率，代表预测是异常实际也是异常的样本数占实际总异常数的比值，即该值越大性能越好。定义FPR为假正类率，又叫假阳率，代表预测是异常但实际是正常的样本数占实际正常总数的比值，即该值越小性能越好。定义TNR为真阴率，表示预测对的负样本数占全体负样本数的比例，TNR= 1-FPR。TP，FN，FP，TN的具体定义如表2 所示。

表2 异常检测结果分类

以具有代表性的 3 组带有异常标签的数据集进行实验分析，实验结果如表3 所示。

表3 实验结果

TP在总样本中有较高的比例，而TN占比较低，说明模型判定标签的正确率较高，模型有良好的可用性，TPR均值在 80% 以上，并且TNR误差率在 0.60% 内，说明模型性能良好，对时间序列数据异常检测有较高的准确性。

3.2 实验二

通过异常检测分析，取汕头市自来水公司2013 年度（该年度的数据具有代表性）日取水量进行分析，分析流程如下：

1）对实验数据进行预处理。

2）对数据进行平稳性检测，可以得到该取水点数据是平稳性时间序列数据，也可以得到模型参数d的值为 0。检测结果如表4 所示。

表4 平稳性数据参数及值

3）通过自相关和偏相关函数，求出p的值为 4 或 5，q的值为 1 或 2，函数图像分别如图7 和 8 所示。

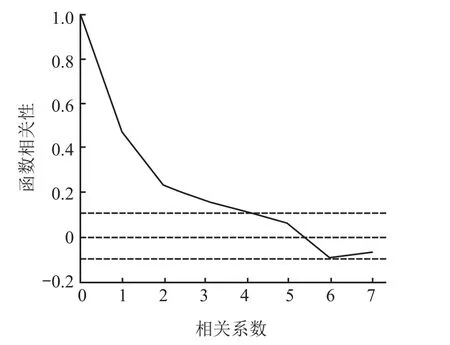
图7 自相关函数图像

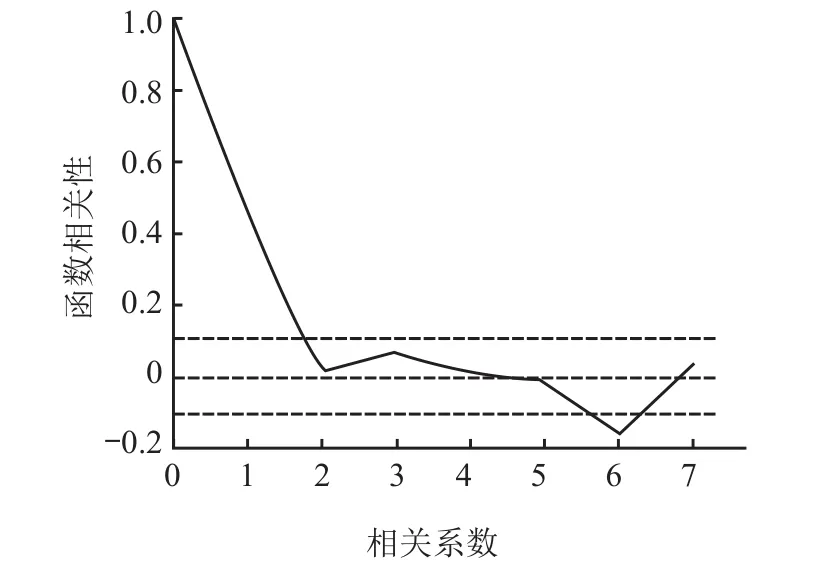
图8 偏相关函数图像

4）通过组合参数p，d，q的值可以找到ARIMA 的最佳组合（4，0，2），拟合曲线图和原始数据并通过时间序列分解算法分解趋势，得到的拟合曲线如图9 所示，分解图如图10 所示。

图9 时间序列数据拟合曲线

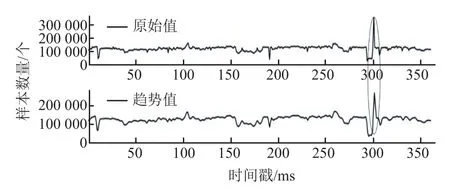
图10 STL 分解图

5）通过 3σ准则和 STL 分解的趋势图可以判断异常值，并通过拟合曲线给出异常值的参考修正值。异常值及参考修正值信息如表5 所示。

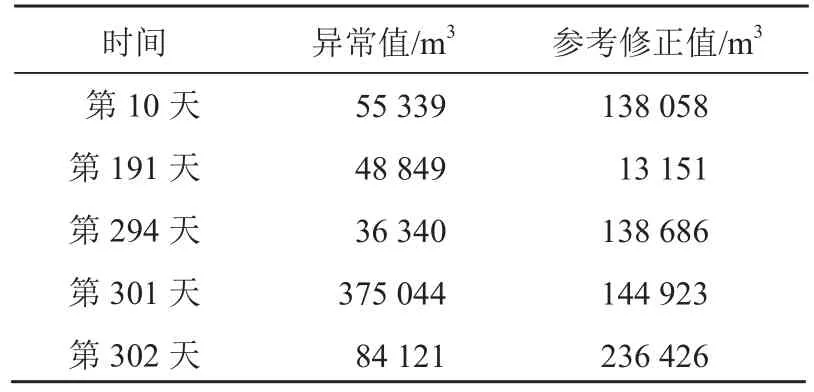
表5 取水异常值及参考修正值

通过汕头市自来水公司 2013 年度的取水异常检测流程，可以找出其他取水机构（如石梁水库、通辽热电有限公司、重庆市渝宁水利水电站开发有限公司等取水点）的异常检测结果，最终结果如表6 所示。

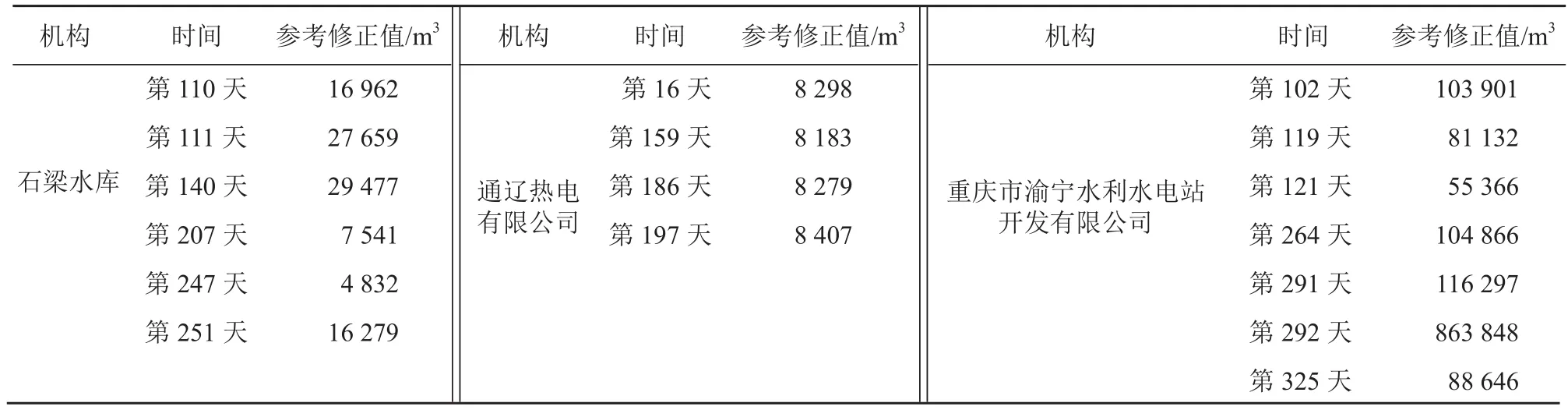
表6 取水异常时间及参考修正值

4 异常值原因分析

日取水量数据的异常值可能导致取水数据的分析出现错误，影响取水点用水决策，以及取用水数据采集整体和数据等质量评价工作的效率。因此，对于异常值的判断可以很大程度地提高取用水的使用效率，通过判断取水异常的原因，可改进取用水的采集方法。

异常数据可能产生的原因很多，经过分析可能的原因如下：

1）取水设备的传感器出现故障；

2）取水设备出现老化，导致取值结果出现较大的误差；

3）取水点的取水操作员出现操作失误；

4）出现自然灾害等非人为因素，导致取水设备严重不符合取水的日常值。

通过对这些原因的分析，每个取水点可以针对产生异常值的原因进行改进，从而提高取水监测数据的质量。

5 结语

以取水异常检测实验为依据，本研究完整指出了以下内容：ARIMA 模型能够很好地模拟日取水量数据关于时间的走势，通过 ARIMA 模型预测值和原始数据的差值可以很好地将时间序列数据转化为非时间序列数据；通过 3σ准则，可以判断出异常值；最后通过 STL 分解取水的时间序列数据，可以更好地判断出异常值。

实验结果表明：本研究可以较好地判断出取用水数据中的异常值，满足工业取水异常检测的需求。未来工作可以对多维数据检测做进一步研究，并逐步提高异常样本的检测率。