基于聚类分析和遗传算法的国际游学路线规划研究:以英国为例
游行键 张建军
(同济大学 经济与管理学院,上海 200092)
国际游学,指的是通过参观国外高校获得知识和体验的游学活动。随着社会和经济的发展,国内游学教育快速增长,在2019年达到3121万人次的用户规模,其中国际游学以每年10%的增速成为主要增长点。在快速增长的同时,学生及家长对行程安排、游学时间等要求也越来越高,研学产品质量不高成为一大问题,提升游学服务质量势在必行。与传统旅游路线规划相比,游学路线规划虽然面临着学生与家长个性化需求和时间约束等多种挑战,但由于高校有排名等公开数据,以及结构化的数据资料,使得基于数据分析的精准路线规划成为可能。相应地,当前基于大数据的游学路线规划也成为改善游学服务质量的重要方向。
另一方面,游学作为一类高速发展的新兴产业,目前相关研究还较为滞后。尚梦杰通过对英国欧陆游学进行研究,认为游学是突破应试教育的一种学习方式,但我国游学产业还不够成熟,需要不断改善产品质量。陈东军等通过梳理以“研学旅行”、“游学”等话题为关键词的文章,认为研究的缺失和游学产业的蓬勃发展形成了矛盾,并认为游学产品开发等方向是今后相关研究的方向。McGladdery等人认为研学旅行行业的研究跟不上目前产业发展的步伐,教育旅行除了对个人发展有利外,还对培养开放、宽容的全球公民有益。谌春玲预测我国留学市场规模可能达到3000亿元并快速增长,但是认为产品设计需要改善,游学选校灵活性差、路线设计不合理等问题给国际游学市场带来挑战。Abubakar等人调查了各国学生参与游学的动机,发现参与游学的理由从未来工作和教育质量到获得签证、了解当地文化等等各不相同。该研究从侧面应证了基于大数据和算法选择个性化游学目的地的重要性。吴水田等通过情境认知理论研究研学旅行如何实现教育功能,认为学生是在和环境的互动中学习的,所以课程设计十分重要,应该合理的选择游学的目的地。
在路线规划方面,目前人们主要关注旅游景点的最优最短路线,如:李景文等使用改进的模拟退火算法解决游客在陌生城市旅游时路线定制问题,并通过混沌寻优进行初始温度设定,降低了陷入局部最优的可能性。劳国炜通过把游客分为一日游和多日游,制定不同的路线来解决高峰期的景区拥堵问题,以鼓浪屿为例使用了其他算法和其改良后的蚁群算法进行比较,得出了其方法可以明显降低拥堵的结论。周福来通过粒子群算法,解决了暑期旅行如何达到最短路线的问题。在算法的比较方面,Halim等人比较了6种用于解决TSP问题的启发式算法,其中遗传算法在计算时间、平均结果和解的方差方面表现优异,因为有交叉和变异算子存在,搜索能力较强,在大规模问题上可以得到比较满意的解。
2 阶段1:目标学校评价
2.1 评价数据基础:QS世界大学排名
本文采用QS世界大学排名作为学校评价的数据基础。这是英国公司Quacquarelli Symonds发表的权威大学排行榜,从2004年开始对全球大学开始排名。QS排名与世界大学学术排名和《泰晤士报》高等教育一样,被认为是全球三大阅读量最高的大学排名之一。QS排名提供的变量如下表所示,其中排名是定序数据,其他得分以100分为满分。
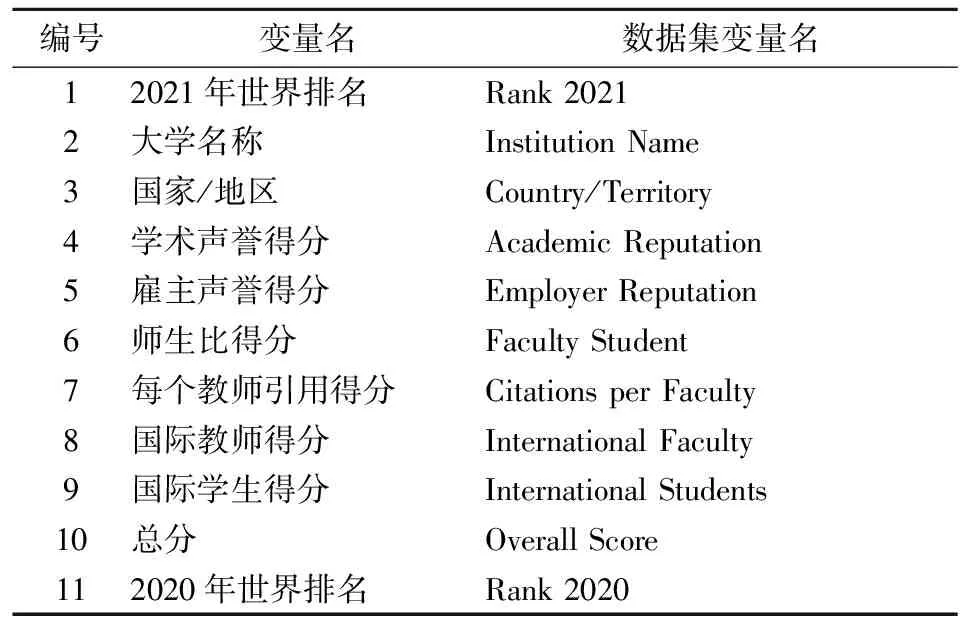
表1 变量解释
2.2 对数据集的因子分析
本次数据中除了所在国家之外都是数值型变量,使用从教育质量排名到专利排名的八个变量进行因子分析。年因子载荷矩阵使用方差最大法进行旋转,使得每个新变量重叠的信息能够最少,旋转后的矩阵如下表所示:
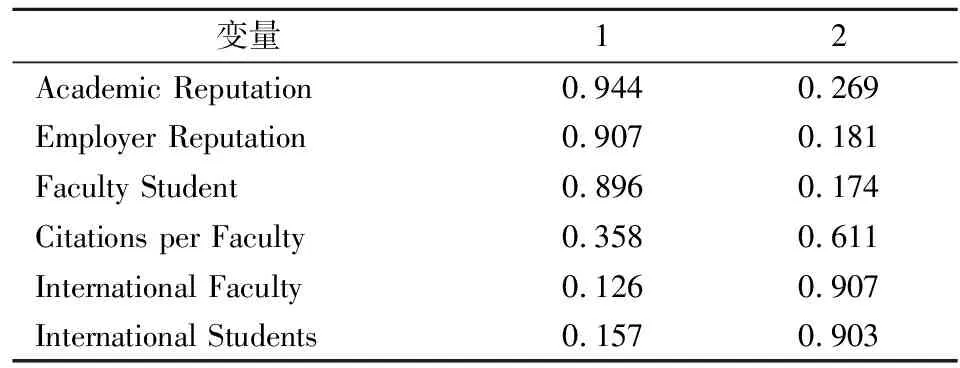
表2 旋转后的成分矩阵
提取方法:主成分分析法。旋转方法:凯撒正态化最大方差法。旋转在3次迭代后已收敛
从上表可以看出第一个指标F1主要是由学术声誉得分(Academic Reputation),雇主声誉得分(Employer Reputation),师生比得分(Faculty Student)等方面组成的,这个指标越高,该学校在学术和就业方面的声誉越好。综上所述,F1这一指标可以命名为综合实力。
第二个指标主要由国际学生得分(International Students),国际教师得分(International Faculty),每个教师的平均引用(International Faculty)和系数为0.269的学术声誉得分(Academic Reputation)组成,这一指标主要反映了国际化程度和单个教师的学术实力,对于之后想在本地就业的同学,该指标影响较小。综上所述,F2这一指标可以命名为国际化程度。
综合以上信息,两个指标分别命名为综合实力和国际化程度。
2.3 对数据集的聚类分析
本次数据集较小,仅仅选取了英国地区的前49所大学,覆盖至QS排名前485的英国所有学校,使用K-Means算法把学校聚类成三类,可以得到下图。
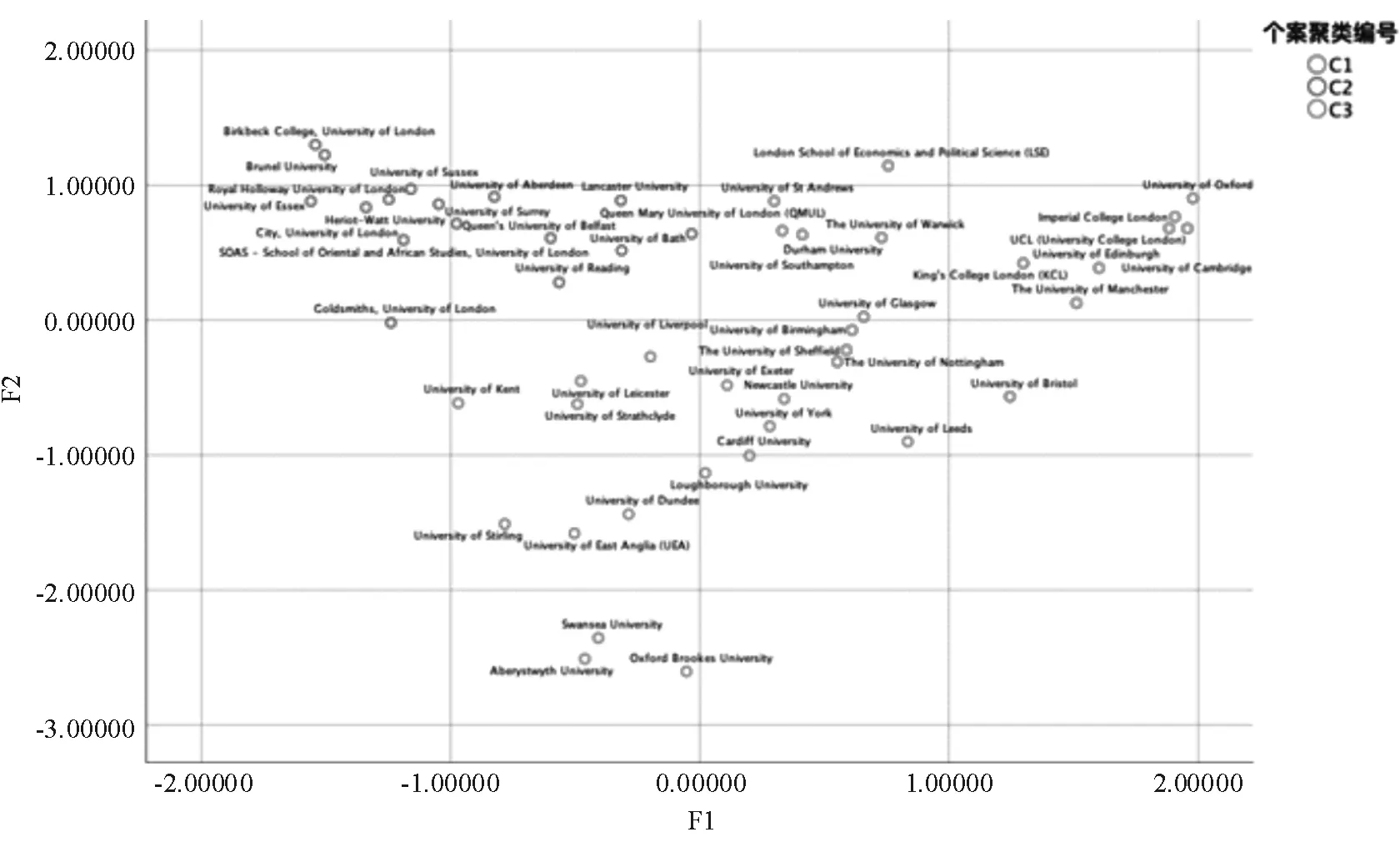
图1 聚类结果散点图
从上图可以得出英国的学校大致可以分为三类,第一类是F1和F2指数都较高的学校,这类学校综合实力强劲,学术声誉和就业方面的雇主声誉都很好。同时这类学校国际化程度高,对于未来想要继续在其他国家深造的同学而言具有优势。于此同时,从上图还可以看出第二个趋势是有一类学校F1适中但是F2低,还有一类学校F2适中F1较低。上图可以看出英国高校基本上是分为三个不同角度,所以本文使用K-Means聚类将其分为三类,分别称之为C1、C2、C3,分类后C1到C3分别有17、16、16所学校。分类的结果如表3所示.
从表3可知,C1类总分(Overall Score)最高,达到74.65分,而第二类与第三类总分接近,都为38分左右。C1类排名平均值为52名,涵盖了英国的主要名校,C2类QS排名平均为183名,C3类综合排名为375名。其中C1类代表了英国的知名高校,综合实力和国际化程度都比较强,C2类代表英国第二类高校,该类高校国际化程度很高,单个教师的文章引用也很强,导致综合排名较高。C3类高校虽然排名不高,但是其综合实力较强,只是国际化水平偏低拉低了排名。
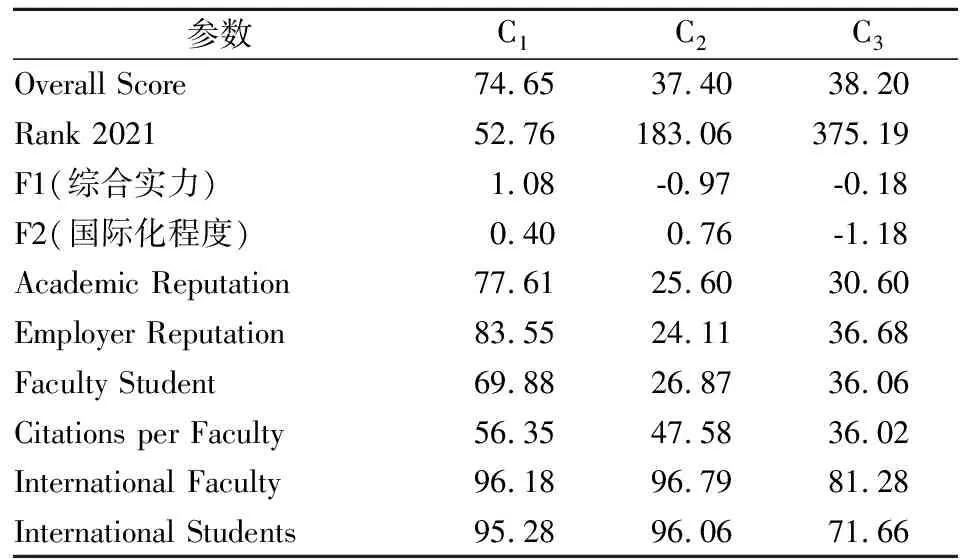
表3 各聚类的参数平均值
综上所述,C1类高校是国际化程度高、综合实力强的名校,适合各项水平都很高的学生游学。C2类高校排名适中,综合实力不如前两类高校,但是国际化程度高,适合想要体验国际化生活的学生。C3类高校属于“性价比”较高的高校,该类学校虽然排名较低,但是学术声誉、雇主声誉都很好,综合实力强。主要拉低排名的因素是国际化水平,该类高校特别适合希望留学之后留在英国工作、生活的同学选择。
通过之前的聚类可以得知,高校可以被分成三类,其中第一类是综合实力和国际化程度都强的名校,第二类是国际化程度高,综合实力较弱的高排名学校,第三类是QS排名底,但是实力较好的“性价比”高校。使用一个矩阵描述这三类英国高校,如下图所示:

图2 大学分布矩阵
3 最短路径规划
3.1 问题描述与假设
由于当前国际游学通常有明确的目标学校需求,大多数游学人群是需要参观名校,因此接下来本文选取图2中C1类17高校作为参观的目标,并基于公开数据探索个性化的最短环游路径。
将选中的所有学校环绕一圈属于旅行商问题,简称为TSP,这样的问题是给定一系列城市和城市间的距离,求访问每一个城市的最短回路,是组合优化中的NP-Hard问题。其数学模型可以表示为在一个城市集C=(c0,c1,…,cn)中每一对城市距离为d(ci,cj)∈R^+,求经过C中每一城市的最短路径R=(cm0,cm1,…,cmn),使得:
min∑n-1i=1d(cmi,cmi+1)+d(cmi-1,cm0)
(1)
旅行商问题有对称和非对称两种,在国际游学问题中通常设定国际往返的距离相同,为对称的TSP问题。
为了明晰问题,补充如下假设:
(1)忽略道路、河流等造成的误差,用两点之间的直线距离计算两点的运输距离;
(2)使用经纬度计算两点的近似距离;
(3)游学活动从C1类某个大学出发,最后回到该城市,并且必须经过且只经过所有筛选出的大学;
(4)游学的路线只形成一个闭圈;
(5)游学路线中往来距离相等。
3.2 游学路线规划模型构建
待游历的n个学校记为一个顶点集合V=(V1,V2,…,Vn+1);学校之间两两相连记为边集合E=(Vij),i,j∈(1,2,…,n+1);学校i与学校j之间距离为dij。记:
(2)
则游学问题的目标函数为:
(3)
约束条件为:
(4)
(5)
(6)
其中式(4)和(5)表示每个节点只有一条边进、一条边出,式(6)表示没有子回路产生。
3.3 蚁群算法设计
TSP问题是NP-Hard问题,求解最优解难度较大,本文采用遗传算法求解,基本步骤如下:
Step 1:对问题进行编码,给出有N个个体的初始种群POP(1);
Step 2:对种群中每一个染色体计算适应度;
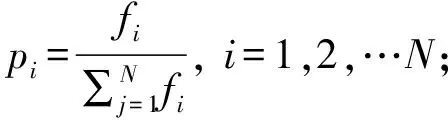
Step4:通过交配,得到有N个染色体的交配后种群CrossPOP(t+1);
Step5:以某个概率p,使染色体的基因发生变异,记为MutPOP(t+1),变异后的种群为新种群POP(t+1),返回Step2
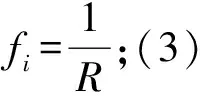
3.4 仿真结果分析
基于C1中的17个学校,位置由其经纬度决定,初始种群大小选择10,不同迭代次数、交叉和变异概率的结果如下:
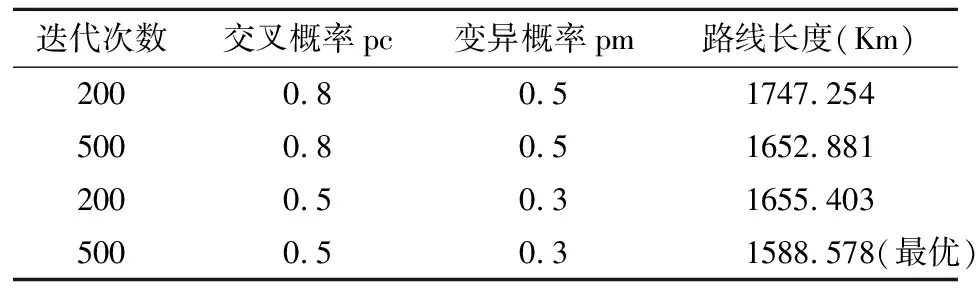
表4 不同参数下的计算结果
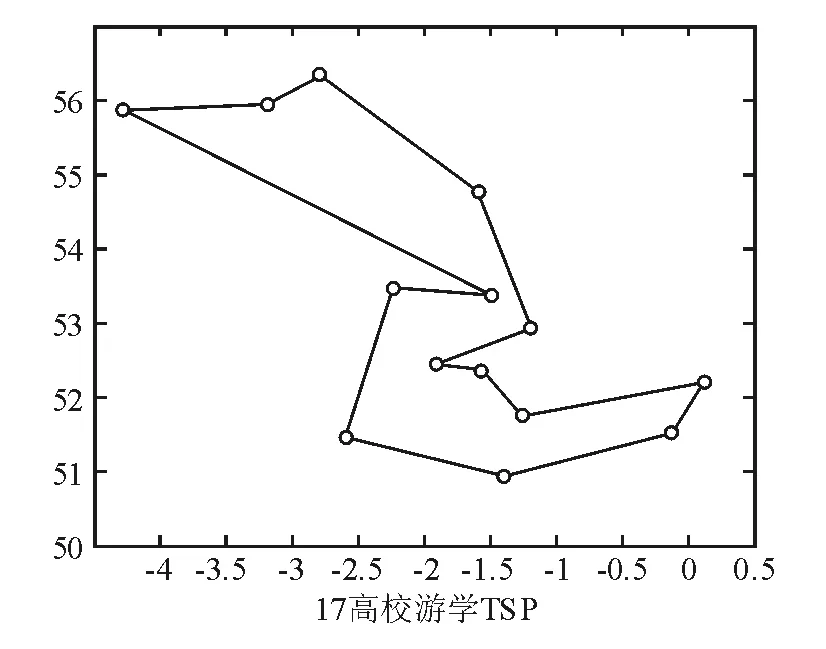
图3 遗传算法所得最优路径图和搜索过程
使用MATLAB编程求解得到表3的结果,可以看到交叉概率在0.5,变异概率在0.3时得到了最优的结果,观察图4的搜索过程可以看到,最优解在迭代超过250次之后几乎没有改变。本算法在多次迭代之后陷入了局部最优,算法没有进行有效的探索。考虑到不同游学人群会在不同学校组中寻找最优路线,应增加算法的搜索能力,避免陷入局部最优成了亟待解决的问题。
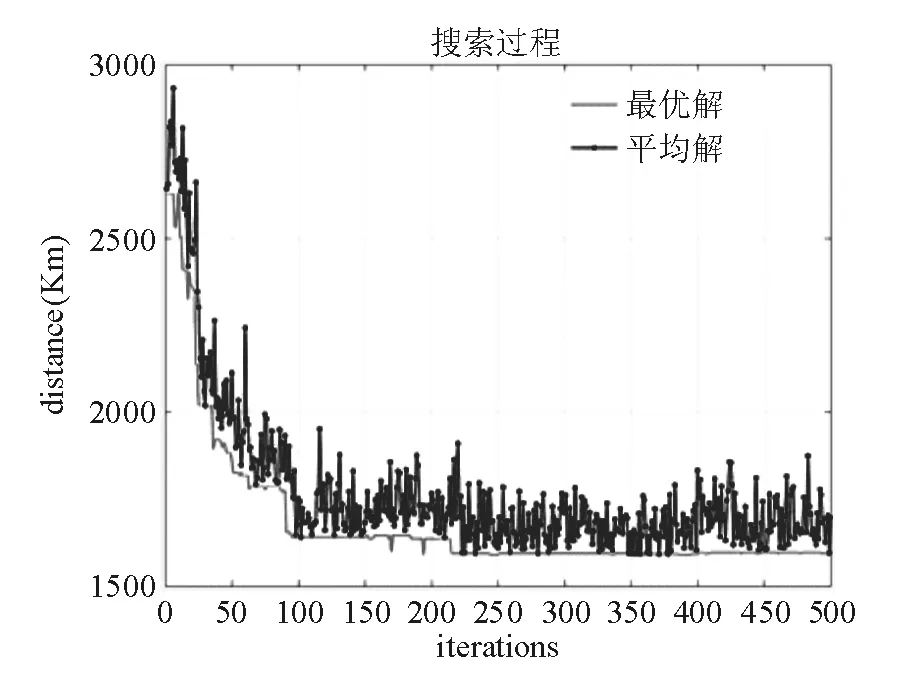
图4 循环200次时最优路径搜索过程
3.5 优化后仿真结果分析
为了解决固定参数遗传算法后期搜索能力弱、容易陷入局部最优的问题,本文通过可变参数的遗传算法来求解最小的路径,参考于莹莹等人2014年提出的基于自适应交叉和变异算子的改进方法对算法进行优化。
在交叉算子方面,早期应该交换概率较大,让种群能够快速搜索各种解,但是在后期,交换概率应该逐渐减小,保留性能较好的基因。为了既让早期保持较大交换概率以保证搜索范围,又让后期交换概率减小以保留优质解,本文将交换概率pc的表达式设置为:
(7)
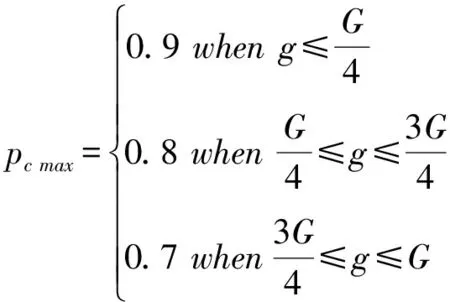
(8)
在变异概率方面,早期种群变异概率应该较小,让方法专注基因的提升,后期的变异概率应当逐渐增大,让解不会过早收敛,跳出局部最优,变异概率具体取值如下:
(9)
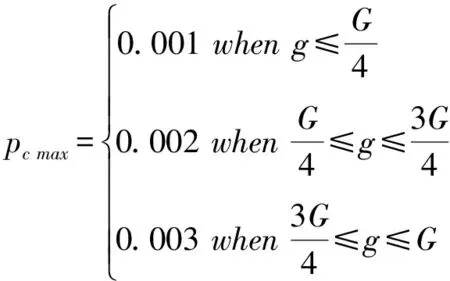
(10)
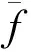
计算结果如下表所示:
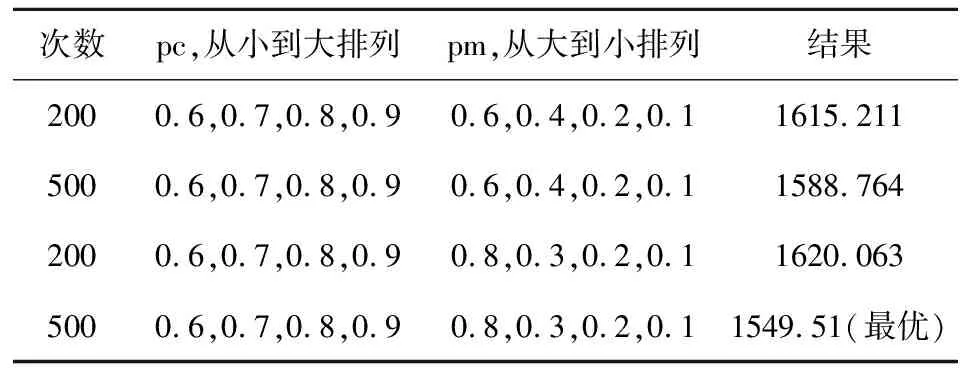
表5 改进的遗传算法在不同参数下的计算结果
可以看到在表格中第二次尝试达到了最优,其搜索过程如图5所示。
和图5相比,改进的自适应参数遗传算法在迭代后期仍旧能够大范围搜索,最终找到了比原算法更优的解。在解决游学最短路径问题上,使用基于自适应算子的遗传算法求解有着更好的稳定性。
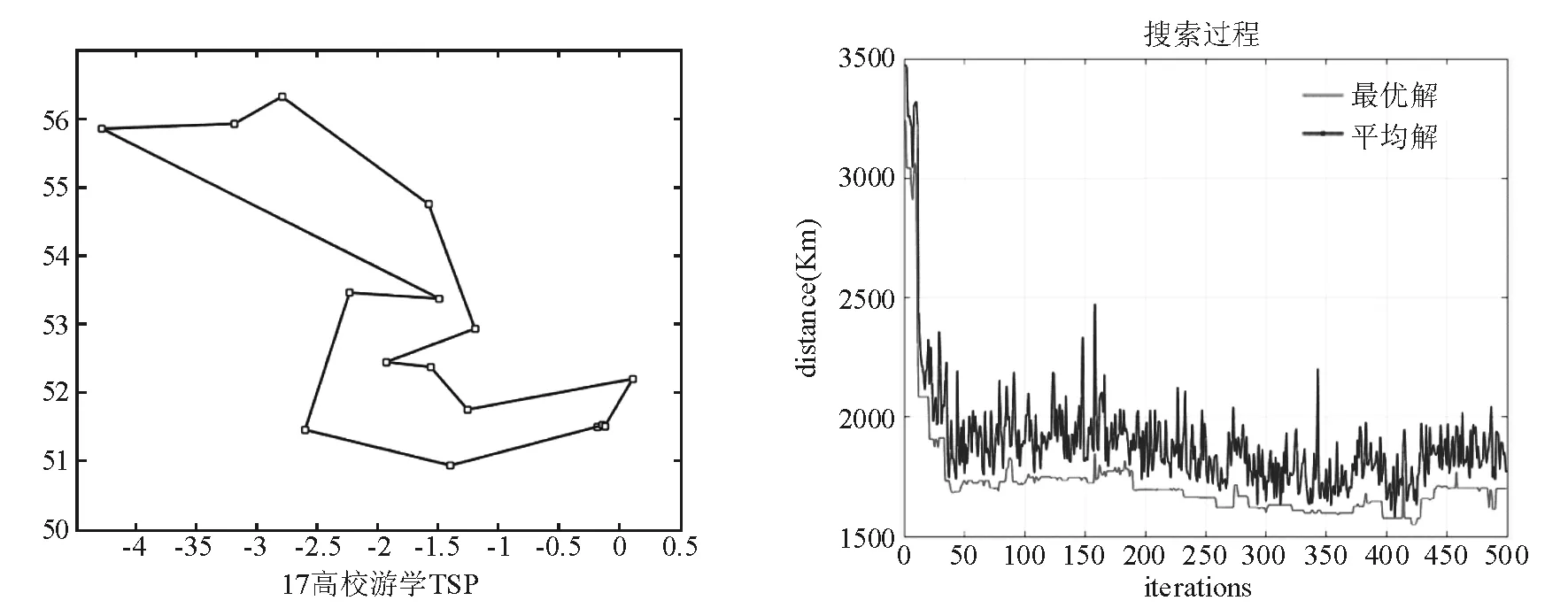
图5 改进的遗传算法的最佳结果和搜索过程
4 总结和讨论
针对国际游学路线规划问题,本文综合运用机器学习和数学规划方法进行分析,首先基于世界大学排名的数据集,采用因子分析方法构建了相对简洁的指标体系,之后使用聚类分析方法对学校进行类型划分,实现了向游学者进行推荐的游学学校集合。在此基础上,如何环游目标学校成为了一类TSP问题,本文首先使用传统遗传算法求解,再通过优化后的遗传算法解决了在迭代后期收敛的问题。
在后续进一步的研究中,可以考虑在更为个性化的需求标签(如GPA、TOEFL和GRE成绩,录取概率等)之下对目标学校进行评价、划分,并

