蓄电池式地下铲运机动力电池的电磁辐射干扰研究

□赵云霄 杨忠炯

为了响应国家节能环保的号召，各种以电能为主要能源的工程机械车辆也如雨后春笋般纷纷问世。然而，就现阶段而言致力于地下挖掘、运输的地下铲运机在新能源领域仍处于起步阶段[1]。目前，新能源地下铲运机一般为装载有电缆的电缆式地下铲运机，电缆式地下铲运机虽然解决了排放和能源的问题，但是由于电缆长度的局限性，导致铲运机的作业距离不能过于远离配电站，从而限制了铲运机的机动性能和活动范围，也限制了运行速度，这无疑大大降低了电缆式铲运机的经济性。为此，提出一种以蓄电池为主要能源的新型纯电动地下铲运机，该电动铲运机能解决传统地下铲运机尾气排放严重造成井下环境恶劣的难题，也能解决电缆式电动铲运机机动性受到限制的困扰。

然而，蓄电池式地下铲运机的动力电池在工作时带来的大电压和大电流很有可能产生比较严重的电磁干扰；而且蓄电池本身体积较大，占用了很大一部分空间，势必导致铲运机内部的电磁环境复杂。以上所述因素很有可能对蓄电池式地下铲运机车载的各类敏感电气设备造成不良影响。本文以蓄电池式地下铲运机的动力电池为电磁辐射干扰源，对其产生的电磁辐射干扰进行研究。目前国内对于蓄电池式地下铲运机的研究还比较少，具有一定的创新意义。

一、电池模组

本文所研究的某型号蓄电池式地下铲运机的动力电池分布情况的三维模型和二维俯视图如图1(a)和图1(b)所示。图1(a)中绿色和黄色模块为提供电能的电池模组，紫红色部分为敏感元件预定放置位置。其余部分为铲运机后车架其他结构的简化模型。

根据电池厂商提供的相关设计方案，该型号蓄电池式地下铲运机需要装载36块电池模组以满足实际工作所需的供电要求。36块电池模组基于铲运机实际结构要求考虑放置在铲运机后车架处。

图1(a) 电池分布情况三维模型

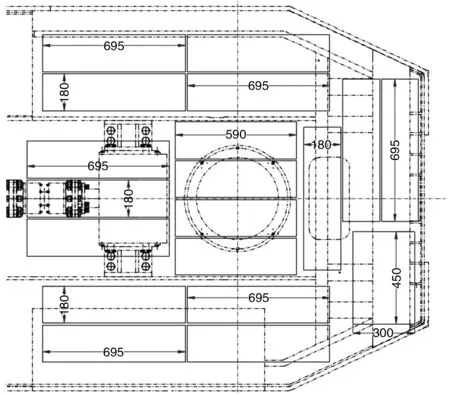
图1(b) 电池分布情况二维图

作为蓄电池式地下铲运机电能动力来源的36块电池模组由两类电池模组组成，分别为I类电池模组和II类电池模组。其中I类电池模组有16个，I类电池模组的单元尺寸为590mm×180mm×220mm，在图1中以绿色部分表示；II类电池模组有20个，II类电池模组的单元尺寸为695mm×180mm×220mm，在图1中以黄色部分表示。I类电池模组和II电池模组的实物如图2(a)、图2(b)所示。

36块电池模组组成一个整体作为铲运机的动力电池，其总电量为205KWh，电压582.4V，电芯类型为LFP(磷酸铁锂)。

图2(a) I类电池模组

图2(b) II类电池模组

基于图1所示铲运机后车架的三维模型可以明显发现，动力电池组占用铲运机后车架的空间较大，势必导致此处空间电磁环境复杂，需要进行系统的仿真计算和研究。

二、电磁场算法和仿真

目前电磁场仿真分析常用的数值计算方法主要有：矩量法、有限元法、有限积分法、传输线法、时域有限差分法等。经过多方面综合考虑，本文所采用的仿真计算的数值计算方法是矩量法。

采用矩量法解决电磁场问题的优点是该方法比较严谨地计算了多个系统之间的互相耦合并且保障了误差系统整体最小从而不产生数值色散，比较适合应用在计算电大尺寸的电磁场问题，非常适合本文所要做的工作。

(一)矩量法的基本原理。矩量法事实上就是将积分方程、微分方程、差分方程转化为矩阵方程，然后对该矩阵方程进行求解的方法[2]。因为求解积分方程、微分方程、差分方程等算子方程的过程中必须要计算矩量，所以该方法被称作矩量法。下面是矩量法求解的具体步骤：

对于非齐次方程

L(f)=g

(1)

式(1)中L是线性的算子方程；g可以是类似于激励源之类的已知函数，f可以是类似于表面电流之类的未知函数。

令f在算子方程L的定义域中展开为一组线性无关的基函数f1，f2，f3，…fn的组合，即：

(2)

式(2)中αn是系数，fn是展开函数或者是基函数。将式(2)代入式(1)，再用L算子的线性我们就可以将公式(1)变为：

(3)

于是，求解f的问题可以变成求解αn。

定义一个合适的内积〈f,g〉，在L的值域里定义一个权函数或者检验函数集合[ω1，ω2，…，ωn]，对每一个ωm在公式(3)取内积，可以得到：

(4)

式(4)中m=1，2，3…。该方程组可写成以下矩阵形式

[lmn][αn]=[gm]

(5)

式(5)中

(6)

(7)

得到了[lmn]和[gm]后，对线性方程组求逆，就可以求出[αn]。

[αn]=[lmn]-1[gm]

(8)

将求出的系数[αn]代入式(2)就可以求出未知函数f。

对于任何一个求解的问题，选择基函数fn和选择权函数ωn都是非常重要的。

基函数fn需要保证其线性独立性，而且基函数的线性组合必须良好地逼近未知函数f。而权函数ωn则需要保证其线性无关，并且已知函数g的相对独立性能决定内积〈ωm,g〉。除此之外，对于基函数fn和权函数ωn的选择也需要考察以下几点：一是矩阵是否能求逆；二是矩阵元素是否容易计算；三是精度的要求；四是矩阵是否为良态。

基函数和权函数的选择是十分关键的。就基函数来说，虽然在理论上可以选取所有保证线性独立性的基函数，但是可以不错地逼近未知函数f的基函数在实际应用中相对较少。

被选择的基函数需要使得矩阵达到下列几个要求：较少的阶次、求逆简单、收敛迅速等。基函数可以分成分域基函数和整域基函数两大类[3]：

(1)分域基函数可以定义为值域存在于未知函数f的所有定义域中，但是有一部分值为0的基函数，比如：

脉冲函数(分段均匀)

分段正弦函数

分段线性函数

(2)整域基函数可以定义为在未知函数f的全部定义域中都存在，且都不为0的基函数，比如

幂级数 fn=x-xn+1

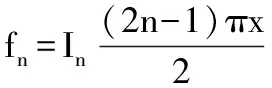
麦克劳林级数 fn=Inx2(n-1)

权函数的匹配方法主要有三种[4]：点匹配法、线匹配法和伽辽金法。

①点匹配法可以定义为匹配位置处于基函数定义域中点位置的方法，这种方法产生的匹配点少而且准确率相对较低。

②伽辽金法所选取的权函数和基函数一样，这样在计算的过程中能得到对称的矩阵从而使得计算的相对误差大大减少。

③线匹配法可以定义为匹配位置在基函数定义域的中线处的方法，这样得到的结果计算精度较高而且计算相对较为简单。

总结一下，矩量法的基本步骤如下：一是将待求的积分、微分、差分等算子方程转为矩阵方程；二是选择一组满足前文所述要求的基函数，将基函数和待求函数线性组合，代入算子方程，从而获得一组代数方程组；三是用适合的匹配方法得到一组权函数，计算所得代数方程组的广义矩量[5]，并转化成矩阵的形式；四是对得到的矩阵方程求逆，将求解得到的系数矩阵代入原方程组，即可得到矩量法的数值解。

(二)矩量法应用于电磁场计算。对于任意介质，麦克斯韦旋度方程为[6]

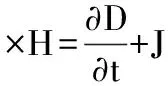
(9)

将理想导体边界条件代入式(9)可以得到电场的表达式为：

(10)

(11)

(12)

式(11)与式(12)中J是表面电流，σ是表面电流密度，J与σ满足以下关系：

∇S·J=-jωσ

(13)

因为在导体表面，电场的切向分量为0，所以可以得到以下式子：

(14)

现运用RWG基函数法求解电场，定义一个表面电流J的函数组合fn，fn满足以下关系：

(15)

式(15)中In是与第n个基函数相关的电流展开系数。

选取检验函数，定义以下内积：

(16)

使用基函数对式(1～14)进行检验，可以得到以下式子：

(17)

使用伽略金匹配法选取权函数，选择的权函数与基函数一致，即ωn=fn。

按照上述矩量法的基本原理可以将电场积分方程转化为矩阵方程，即：

[Zmn][In]=[Vm],m,n=1,2,...,N

(18)

矩阵[Zmn]与矩阵[Vm]确定后就可以解出式(18)中的[In]，得到电场的解。求解磁场的步骤类似故不再赘述。

(三)仿真计算电池的电磁辐射。目前市面上有各式各样的电磁仿真软件，这些仿真软件各有优劣。本文在诸多电磁仿真软件中所选用的软件是FEKO软件。FEKO软件由南非EMSS公司开发，采用的主要数值算法有矩量法、多层快速多极子算法、有限元法、PO算法、并行UTD算法等，帮助从业者系统地进行电磁分析研究[7]。

FEKO软件针对性较强，十分适合车辆的电磁环境建模和仿真，该软件采用了本文所选取的数值计算方法，矩量法，而且还拥有快速多极子算法，极大地提高了计算效率，比其他仿真软件更加适用于电大尺寸的电磁仿真分析，非常适用于本文所要做的工作。

选取好合适的电场仿真软件之后则可以开始进一步的工作。利用SolidWorks建模软件建立好的铲运机后车架的三维模型并转换成x_t格式的文件。将转换好的x_t格式文件导入到FEKO系列软件的CADFEKO软件中，对铲运机后车架各个结构的相对介电常数进行设置。在CADFEKO软件中将导入的铲运机后车架三维模型进行网格化处理。如果单纯地考察计算精度这一层面，那么网格化程度越密，则计算造成的误差越小，可如此一来计算的复杂程度将会变的很大，工作效率也会大大降低。但是，如果网格化的密度太疏又会导致计算不够精确，从而影响仿真结果的准确性。

所以，在选择网格化计算精度时需要同时考虑到计算精度要求和实际条件的计算限制。本文在综合考虑之后选取到了一个合适的计算精度，使其既能满足预期的计算精度要求又能避免多余冗杂的低效率计算，提高计算效率。

做完上述工作后，在电池分布的位置添加相应的辐射干扰源，将其参数调整到与动力电池工作时一致，电压582.4V，电芯类型LFP(磷酸铁锂)，电量205kWh。仿真频率范围设置为1Hz～300kHz，步长为2kHz。利用FEKO仿真软件计算距离后车架左侧面550mm、距离后车架尾部197mm、距离后车架底部高345mm位置处的电场分布和磁场分布，该处为敏感元件初步设计的安装位置，然后仿真计算观测点处水平面整体的电场强度和磁场强度，考察敏感元件安装位置的最优解。

观测点处电场强度仿真结果如图3所示。可以得到观测点处电场强度峰值时频率为38kHz，查看该频率下观测点所在水平面上整体的电场强度分布仿真计算结果，其具体仿真结果如图4所示，图4中黑色圆点为观测点所在水平面中观测点的位置。

观测点处的磁场强度仿真结果如图5所示。可以得到观测点处磁场强度峰值时频率为90kHZ，查看该频率下观测点所在水平面上整体的磁场强度分布仿真计算结果，其具体仿真结果如图6所示，图6中黑色圆点为观测点所在水平面中观测点的位置。

图3 观测点电场强度仿真结果

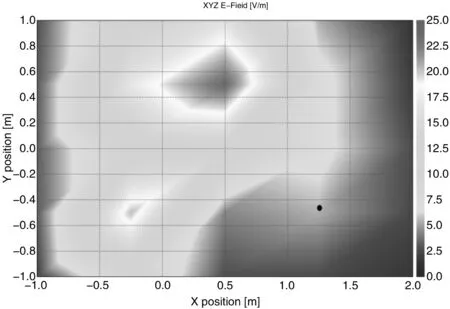
图4 38kHz时整体电场强度分布仿真结果

图5 观测点磁场强度仿真结果

图6 90kHz时整体磁场强度分布仿真结果

根据以上仿真结果可以得出：

(1)敏感元件处的电场辐射值的范围是0～6.7V/m，磁场辐射值的范围是0～5.8A/m，已经超出了该处敏感元件的抗干扰限值5V，可以初步认定需要对蓄电池铲运机的动力电池工作时产生的电磁辐射进行有效的抑制处理。

(2)敏感元件所在安装位置需要进行调整，定义后车架前后方向为X方向、左右方向为Y方向。根据电场、磁场整体分布仿真结果来看，将敏感元件安装位置在X方向上左移400mm，在Y方向上下移150mm会更加理想。

三、结语

本文以某型号蓄电池式地下铲运机为研究对象，研究其动力电池的工作时产生的电磁辐射干扰。经过分析、建模、选取仿真软件、进行仿真计算、研究仿真结果等工作，最后初步认定动力电池工作时产生的电磁辐射需要得到抑制。电磁辐射的抑制措施初步可以主要考虑使用铝或者铜制箱体屏蔽隔离干扰源、屏蔽保护敏感元件、对敏感元件的安装位置进行调整让敏感元件远离辐射源等方法。