基于遗传算法的集中式电采暖系统优化研究

杨卓 宫铭远 周志刚 谌薛蛟

1 哈尔滨工业大学建筑学院

2 寒地城乡人居环境科学与技术工业和信息化部重点实验室

0 引言

近年来，社会对环境污染和能源短缺等问题的关注推动了清洁能源技术的快速发展，太阳能、风能等能源补给了一部分的电力需求。然而我国大部分地区仍面临电力负荷不均，电网峰值调节能力差等问题[1]。电采暖负荷在满足舒适温度的基础上，在某一时间段内，具有对功率及能量的调控区间，该特点具有较大的用能需求弹性。因此将电负荷作为运行调节的目标，具有较为可观的响应速度以及较大的调控能力。国内外学者已对电采暖方面的问题进行了大量的研究，并取得了丰富的研究成果。通过建立电采暖负荷预测模型[2]，对电网实现移峰填谷及电力系统的调频调压提供了精确判断和理论指导，有效的消纳了弃风电量[3]。

针对电采暖系统的运行策略，大都采用的是基于用户实时室温的自反馈调节，即通过温控设备监测实时温度与设定温度的差值来决定是否开启电热设备。该方式充分发挥了电采暖的灵活性，但未能考虑用电成本。尤其对于公共类建筑来说，采暖负荷主要集中在白天，夜晚随着采暖负荷的降低，其消纳电网多余电量的能力也随之变弱。若能消纳夜间谷电产热，利用建筑围护结构本身的蓄热能力储存热量，并在白天释放出来，将会降低电网白天的峰值负荷，提高电采暖的经济性。

本文通过建立电采暖优化仿真模型，确定电热设备的启停方案，通过遗传算法代入模型及约束条件进行可行性验证，最后以实际工程为例进行模拟对比，分析优化后该集中式电采暖系统在能耗及经济性等方面的优势。

1 建立电采暖优化仿真模型

为实现复杂数学模型的简单计算，将借助仿真软件Simulink 对建筑及系统信息进行处理。Simulink 中包含完整的室内温度计算过程，主要包括室外温度输入模块、太阳辐射计算模块、建筑围护结构动态传热模块、户间传热计算模块、室温设定模块、电热膜及控制开关模块、热负荷计算模块等。

1.1 目标函数

电采暖系统运行策略优化的目的是为了降低运行费用，因此需设置经济性优化目标函数，求得模型最优解：

式中：Ph为电热膜功率，W；Δx为电热膜加热时间，min；Ct为t时段的电价，元/kWh。

由式（1）可看出，电热膜总功率的增加会提高系统的运行费用。目前，电采暖系统主要根据室内温度与设定温度的差值来判断是否开启电热膜，在对房间的加热过程中，电热膜总功率恒定且高于实时热负荷。房间达到设定温度时，电热膜停止工作，其余热会使室内温度继续升高1～3 ℃，造成一定的热量浪费[4]。为降低房间能耗，提高电能利用率，需要做到电热膜功率与房间实时热负荷相匹配。由仿真软件计算出实时热负荷Qh，根据式（2）得到此时需开启的电热膜数量N（向上取整）。

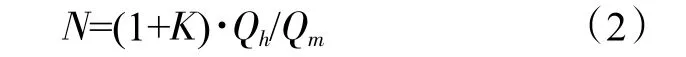
式中：N为所需电热膜数量，片；Qh为房间的计算热负荷，W；Qm为每片电热膜对供暖房间的有效功率，W，上下传热比例取0.85；K为附加运行系数，取0.2。

则可得到此时电热膜的总功率Ph，代入室内空气动态热平衡方程式，计算出此时的室内温度：

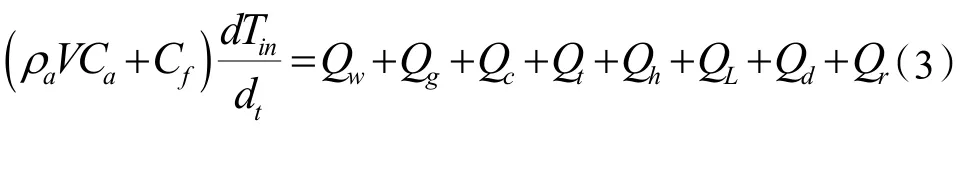
式中：ρa为相对室外温度下的空气密度，kg/m3；V为房间的内部体积，m3；Ca为相对室外温度下的空气比热容，J/(kg·K)；Cf为建筑内家具热容量，J/(kg·K)；Tin为室内空气温度，K；Qw为通风换气造成的热损失量，W；Qg为墙体耗热量，W；Qc为门、窗耗热量，W；Qt为冷风渗透耗热量，W；Qh为室内热源提供的热量，W；QL为户间传热量，W/m2；Qd为荧光灯散热量，W；Qr为人体显热散热量，W。

1.2 约束条件

该优化函数的约束条件包括显式和隐式[5]，显式约束条件要求正常运行的电热膜的功率在式（4）范围内，且当前时刻的功率与前一时刻的功率差值需满足式（5）。隐式约束条件即电热膜工作时需满足室温及组数的计算要求，见式（2）。

式中：Ph，t为t时刻电热膜的功率，W；Phmax为电热膜最大功率，W。

式中：ΔPmin为电热膜出力的额定向下爬坡速率限值，W；ΔPmax为电热膜出力的额定向上爬坡速率限值，W。

另外应设计室外温度约束，防止在分组启动时电热膜频繁开启降低使用寿命，设定当室外温度变化5 ℃时，电热膜计算模块启动，重新计算此时所需的电热膜组数，见式（6）。

式中：Tout,t为t时刻室外温度，℃；Tout,t-1为t-1 时刻室外温度，℃。

1.3 优化模型

综上所述，电采暖建筑完整的运行优化模型为：

2 遗传算法的设计

遗传算法是根据达尔文进化论中的自然选择和遗传学机理所衍生出来的计算模型，通过模拟自然进化的过程找寻最优解，广泛应用于机器学习、自动控制等领域。相对于常规的算法，遗传算法能够较快地求解复杂的组合优化问题，并且获得较好的优化结果[6]。针对本文的研究内容，选择计算能力更强、计算效率更高的二进制编码，其对应的初始种群函数为crtbp。

2.1 设计算子

选择算子选取在遗传算法中使用最多的轮盘赌法，这种方法是一种回放式随机采样方法。具体的操作是在当前种群中，将每个个体的适应度值与种群中所有个体的适应值之和相比，如式（8）所示：

式中：Pi为第i个个体被选中的概率；f(xi)为第i个个体的适应度值；n为群体中的个体数。

变异算子选择适合二进制的基本位变异方式，即是以变异概率对个体编码串中的某一位或者几位基因座的值做随机变异运算，其具体操作如下：

1）以变异概率指定个体每一个基因作为变异点。

2）在二进制编码中，对每一个指定的变异点的基因值取反运算，从而得到新的个体。

交叉算子选择单点交叉的操作方式，其特点是简单易行，适用于二进制的编码方法，具体的操作过程如下：

1）对中群中的所有个体两两随机配对，若群体大小为M，则形成M/2 对配对组。

2）在配对后的每个个体中，随机设置某一基因座之后的位置为交叉点，即若染色体长度为N，则会有N-1 个交叉点位置。

3）对每一对配对的个体，根据设定的交叉概率在其交叉点处交换染色体，从而形成一对新的个体。

2.2 选择优化参数

为充分利用建筑物的蓄热特性和峰谷电价的差值优势，需要对电热膜的启停时间进行优化，使其尽量在低电价时段进行加热，达到节省电费的目的。黑龙江省电业局提供的哈尔滨市峰谷平电价Ct变化情况，如图1 所示。

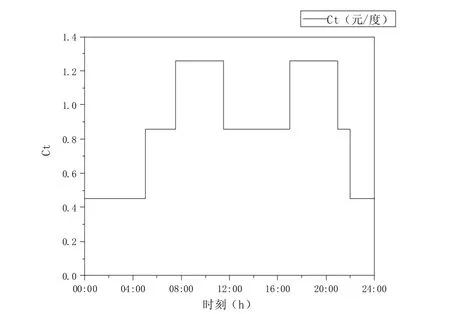
图1 哈尔滨市一天内电价变化情况

选取每个不同电价阶段的电热膜启停时间点X=[x1,x2,…,x14]T为优化变量（其中角标为奇数的时间点为启动时间，偶数为关闭时间)，F(x)为优化目标函数。将每阶段电价，电热膜的功率以及启停时间点代入式（1）中得出目标函数具体表达式如下：

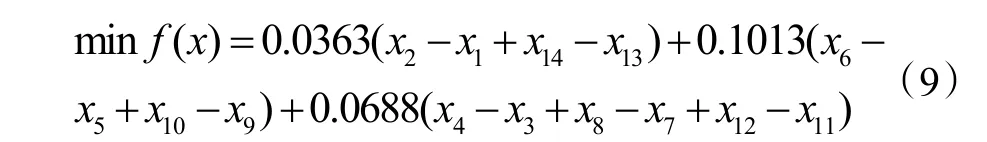
式中：xi为第i个电热膜启（停）时间点，其取值范围如下：（0＜x1＜x2≤300，300＜x3＜x4≤450，450＜x5＜x6≤690，690＜x7＜x8≤1020，1020＜x9＜x10≤1260，1260＜x11＜x12≤1320，1320＜x13＜x14≤ 1440）

2.3 建立罚函数

建立罚函数的目的是在计算非最优解个体的适应度时，对其适应度的值附加上一个惩罚因子，降低其适应度，使其不满足被遗传到下一代的要求。工作时间，考虑到房间对实际室温的需求，加入罚函数来对遗传算法结果进行限制。罚函数的判定见式（10）。

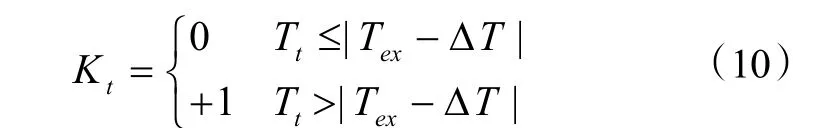
式中：Tt为t时刻的室内温度，℃；ΔT为室温波动值，取2 ℃；Tex为设定温度，其具体表达式为：

结合罚函数后的目标函数式（1）应变为：

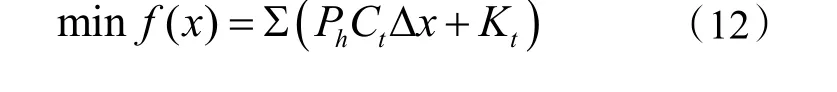
3 模拟结果分析

3.1 工程概况

该工程为哈尔滨市某教学建筑，其总建筑面积为2059.87 m2，地上三层，一层层高3.6 m，二、三层层高为3.3 m。该建筑为电热膜沿地面敷设的电采暖系统，其采暖设计参数如表1 所示。

表1 采暖设计参数

该建筑的设定温度值如图2 所示，0:00-4:00为建筑的非使用时段，设定温度较低为14 ℃。4:00-7:00 设定温度提高至 16 ℃，对房间进行预热。7:00-15:00为学生集中上课时间，室内设定温度提升至 18 ℃，满足设计要求。15:00-20:00，房间使用率降低，温控器设定温度降低至16 ℃，减少电能耗费。20:00-24:00为非使用时段，因此降低设定温度至14 ℃。

图2 温度设定值变化图

3.2 验证仿真模型

为验证仿真模型的准确性，选取教室B为模拟对象，模拟时间为 2018 年12月 10 日至 2018 年12月14 日，得到室温的仿真计算结果，并将模拟值与实测值进行对比，如图3 所示。

图3 10-14 日模拟室温与实测室温对比图

5 日内模拟值与实测值的最大误差与标准差如表2 所示，最大误差不超过1.5 ℃，标准差不超过 1 ℃，说明该仿真模型具有较高的模拟精度，可满足工程的实际应用。

表2 模拟室内温度的最大误差和标准差

3.3 室温对比分析

将遗传算法对运行策略的优化结果代入 Simulink中的温度设定模块，得到图4 所示的室温对比情况。以10 日为例，优化后室温与实测室温的差值主要集中在 0:00-7:00 左右，原因是低谷电价时段，在经济性函数和遗传算法的约束下，电热膜全部开启用于加热房间，导致优化后的室温高于实际运行室温。两者差值在4:00 时最大，为2.98 ℃，之后差值逐渐缩小，是因为实际运行情况下电热膜从 4:00 开始预热，房间内温度开始升高。在房间的使用时间内，优化后的室温整体呈下降趋势，电热膜开启时间减少，但其与实测室温的差值始终保持在± 2 ℃以内，满足室温波动要求。

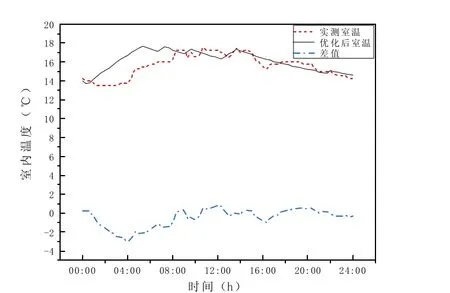
图4 10 日优化后室温与实测室温对比情况

3.4 能耗对比分析

仍以10 日为例，从图5 的房间耗热量对比图中可以看出，低电价时段，优化后的耗热量持续上升且斜率保持不变，该时段电热膜全部开启。7:00-12:20 房间耗热量不再增加，电热膜停止工作，建筑在夜间储存的多余热量在不断释放，使房间温度能够达到设定要求。12:20 分时室温降低至 16.3 ℃，为满足舒适度要求，电热膜开始工作，直至 13:40 分温度提升至17.1 ℃，此后电热膜保持关闭。15:00-20:00 电热膜不工作的原因是，15 :00 后房间设定温度由18 ℃降低至 16 ℃，在遗传算法的约束条件下电热膜的启动温度也由 16 ℃降低至14 ℃，该时段内房间室温始终高于14 ℃，因此电热膜未开启。整体来看，优化后电热膜的日耗热量要低于实际运行的日耗热量，同时在白天使用时间内，优化后的室温与实际室温的差值始终在±1 ℃范围内，说明经遗传算法优化后的电热膜运行方案在降低采暖能耗的同时也保证了人体的舒适性要求。

图5 10 日优化前后房间耗热量对比

从图6 中可以看出，在10-14 日中，采用遗传算法优化后运行能耗普遍小于优化前，五天的时间内节省了55137 kJ 的能量。

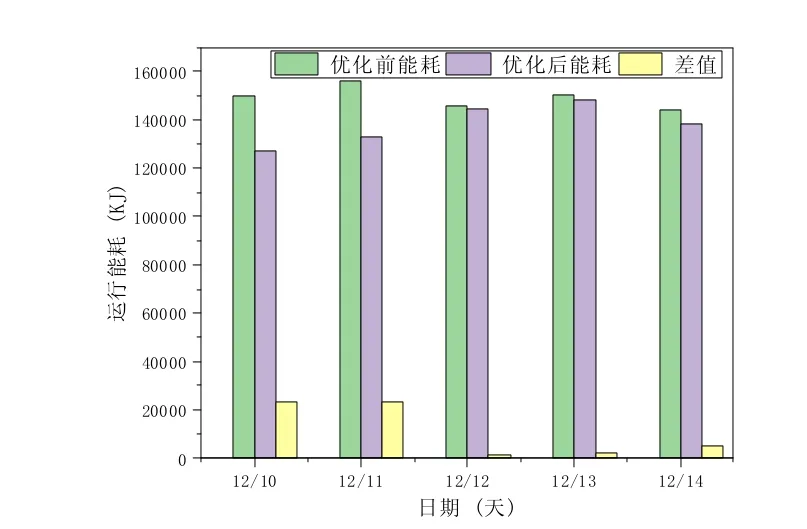
图6 10-14 日优化前后能耗对比

3.5 经济性对比分析

10-14 日优化后的供暖电费与实际运行的供暖电费对比如图7 所示，遗传算法优化后的运行策略在一周的时间内共节省了9.2 元供暖电费，主要是因为电热膜集中在夜间谷电期间对房间进行加热，在用电高峰时期减少电热膜的开启，充分利用电价差的优势。

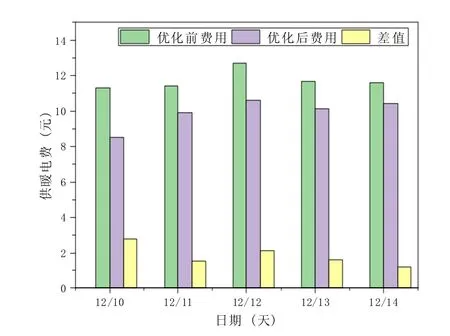
图7 10-14 日供暖电费对比

根据典型房间10-14 日的电费情况，对整栋教学楼全采暖期供暖电费进行估算。供暖电费的计算公式如下：

式中：Cq为全采暖期供暖电费，万元；W为日平均电费，元/ 天；A′为典型房间面积，m2；A为教学楼总面积，m2；N为运行天数，天。

由式（13）计算出优化前总供暖费用为 7.15 万元，经遗传算法优化后的电采暖运行策略的供暖费用为6.01 万元，整栋建筑在采暖期内节省了约1.14 万元。

4 结论

1）本文建立的电采暖优化仿真模型通过设置经济性目标函数和约束条件来调整电热膜的开启组数，并结合遗传算法通过设置优化参数和罚函数控制电热膜启停时间点及室温允许波动值，通过实际工程案例验证了该仿真模型的准确性。

2）电采暖在实际运行过程中依靠温控器将室内温度迅速提升至设定温度，加热时间过短，不能充分利用建筑物的蓄热特性。而经遗传算法优化后的电采暖系统能够在电价低谷时段对房间集中加热，达到设定温度值后并不停止，利用围护结构的蓄热能力将多余的热量储存起来，并在白天使用时间内将热量释放到空气中，降低了电热膜启动的频率，满足室内温度要求的同时节约了电能，降低了采暖期的运行费用。