Reliability evaluation of PMS considering coupling effect of functional and physical dependency

Ying CHEN ,Qicho MA ,Rui KANG

a Science and Technology on Reliability and Environmental Engineering Laboratory,Beihang University,Beijing 100083,China

b Institute of Electronic Engineering,China Academy of Engineering Physics,Mianyang 621999,China

KEYWORDS Functional dependency;Phased-mission system;Physical dependency;Reliability evaluation;Stochastic degradation process

Abstract Aviation and aerospace system are typical Phased-Mission Systems (PMSs) featured with varying configuration,phased load condition and cross phase failure correlation.The coupling effect of Functional Dependency(FDEP)and Physical Dependency(PDEP)has a unique influence on the failure behavior of PMS.In this article,the coupling effect is analyzed,and the degradation of components is modeled with the positive drift wiener process,in which the drift coefficient is related to environmental conditions and operation stress.Finally,failure behavior and system reliability are simulated.An avionics controller is studied as a case,with the degradation time distribution model and simulation algorithm,the coupling effect and dynamical system reliability can be achieved.Results show that this modeling method can describe the coupling effects of FDEP and PDEP and their influence on the failure behavior and reliability of the PMS system.

1.Introduction

In the complex system reliability evaluation area,increasing attention has been drawn to the phenomenon known as failure dependency,for it may decrease system reliability because of joint-failure probability.These dependencies include Common Cause Failure (CCF),Functional Dependency (FDEP),and Physical Dependency (PDEP) et.al.Each type includes a variety of correlations.In addition,these dependencies may have coupling relationship with each other.Ignoring these correlations may lead to inaccuracy of reliability evaluation,and will affect the testing,maintenance,and monitoring of complex systems.

FDEP is defined as the functions of some components (referred to as functional dependent components) rely on the function of other components(referred to as functional trigger components).The failure of one trigger component causes other dependent components within the same system to become unusable or isolated from the system.For example,the failure isolation effect,as a kind of FDEP,occurs from one failure component and causes other components unusable from the system.Extensive work about the reliability modeling of system with FDEP has been done.Nidhal et al.presented a mathematical model of system reliability and selective maintenance policy considering FDEP.Yang and Sankarpresented an automatic FDEP and reconfiguration methodology to locate some failures which cannot be located by the traditional method,which significantly increase the reliability of a network system.Xing et al.proposed a combinatorial method based on the divide-and-conquer paradigm and total probability theorem for addressing the FDEP in the reliability analysis of fault-tolerant systems with imperfect fault coverage.

Propagated failures are CCF originated from a component of a system causing the failure of the entire system.There exists a competition in the time domain between the failure isolation and propagated failure effect.This coupling effect has been widely analyzed for binary system,multi-state system,multi-trigger binary systems,and multi-trigger multi-state systems.Xing and Levitinproposed a combinatorial analytical method based on the generalized SEA method to analyze the reliability of system subject to competing failure propagation and FDEP.Zhao and Xingextended this work and proposed a new method for the reliability analysis of competing systems subject to cascading FDEP and random failure propagation time.Nidhal et al.proposed an optimal selective renewal policy for systems subject to FDEP and propagated failure with global effect.

Phased-Mission Systems(PMSs)are systems in which multiple non overlapping phases or missions must be accomplished in sequence.The competition effect of failure isolation and propagated failures have also been studied in PMS.Levitin et al.proposed a recursive and exact method for reliability evaluation of PMS with multiple,consecutive,non-overlapping phases with propagated failure.Wang et al.studied the competition effect between the failure isolation and propagated failure effect in PMS,and modeled the effects of phase-dependent,probabilistic competing failures,with multiple-valued decision diagrambased combinatorial method.Different FDEP groups can be dependent due to sharing some common components;they may appear in a single phase or multiple phases.Wang et al.modeled and analyzed the reliability of PMSs with functional dependence in one phase and multiple phases..

PDEP is the effect of some system components(referred as the physical trigger components) affect the degradation process of other components(referred as physical dependent components) by changing the environmental conditions,such as thermal,chemical,or electromagnetism conditions et al.PDEP can be observed in all kinds of complex system,for example,in electronic system,an active component can affect its surrounding environment through ways like conduction,radiation,and then influence the development of failure in other components.After the active component fails,the physical effect disappeared.Chen et al.studied the FM dependences and categorized them as competition,trigger,acceleration,inhibition,damage accumulation and parameter union.They also studied PDEP in complex systems,such as k-out-of-n systems,multistate system,multi-phase system,cold-standby systemand system with imperfect fault coverage effect.Zeng et al.proposed a compositional method to predict system behavior considering failure mechanism collaboration.Chen et al.studied the coupling failure behavior between adhesive and abrasive wear mechanism of aero-hydraulic spool valves.

From the above discussion,it can be seen that extensive work has been done on reliably evaluating of systems with FDEP and PDEP effects respectively.The coupling effect of FDEP with CCF has also been studied in complex system including PMS.However,very few works have been done on the coupling effect of FDEP and PDEP in PMS.In this paper,the concept of the coupling effect of FDEP and PDEP will be clarified,and the influence of the coupling effect on system failure behavior will be discussed in detail.A combinational method of continuous stochastic process and Monte-Carlo simulation are applied to describe the dependent behavior and evaluate the dynamic reliability.Finally,an avionics controller as a PMS will be studied to verify the validity of the proposed method.

The remainder of this paper is organized as follows.Section 2 explains the problem of the FDEP and PDEP effect in PMS.Section 3 illustrates the stochastic degradation model of the component and models the coupling effect phase by phase,evaluates the system reliability with the total probability formula.Section 4 is a case study of an avionics controller system.Finally,the conclusions of this paper are summarized in Section 5 and the future studies are outlined.

2.Problem description

The coupling effect of FDEP and PDEP in PMS system is mainly due to the cross-phase dependencies of system components and the phased system configuration.Due to the complexity of the problem,a simple structure is taken as an example to illustrate the coupling relationship.As shown in Fig.1,components,,,andform a system,if the system only performs a single mission without different phase,the structure is shown in Fig.1(a).The trigger componentand the dependent componentform a functional dependence group,where the failure ofwill result in the unavailability or inaccessibility of.Meanwhile,,and componentandconstitute a physical dependence group,that is,the degradation process ofandwill affect the degradation rate ofand.If the failure ofprecedes’s,is isolated in the system and cannot be used,neither the PDEP originating fromnorcan be triggered.However,when the failure ofprecedes’s,the PDEP originating frommay still continue to affect the rate of degradation ofand.

If the above system is a PMS,which includes 3 phases to complete the whole mission,which is shown in Fig.1 (a)-(c).Suppose a mission starts atand ends at.In phase,,,,andare all required to be in the operation state.In phase,andare in the operation state.In phase,or,are in operation state.Componentsandare connected in series in the system but can work independently according to mission requirements.

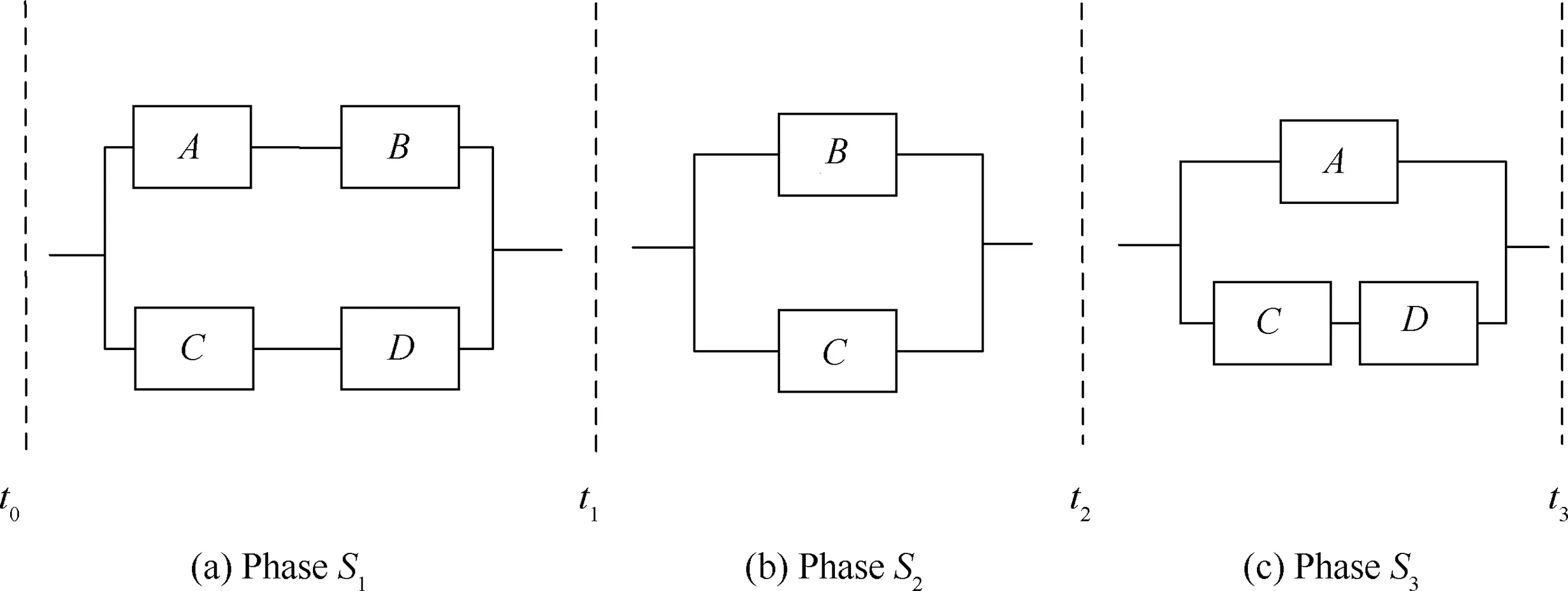
Fig.1 System consisting of four components.

The independent failure sequence of,,andis determined by their degradation process individually,but in a PMS with complex dependencies,the failure sequence is also related to the system configuration,which will have lots of possibilities.Take the case of＜t＜t＜t=tas an example,the degradation and degradation rate of component,andare shown in Fig.2,where t, t, t, trepresent the time when the degradation value of component,,andreach the degradation threshold.Because the influence of coupling effects onis similar with,in Fig.2,is neglected.However,due to the different phase configurations,the degradation process ofis different from,which will be talked about in the case study section.

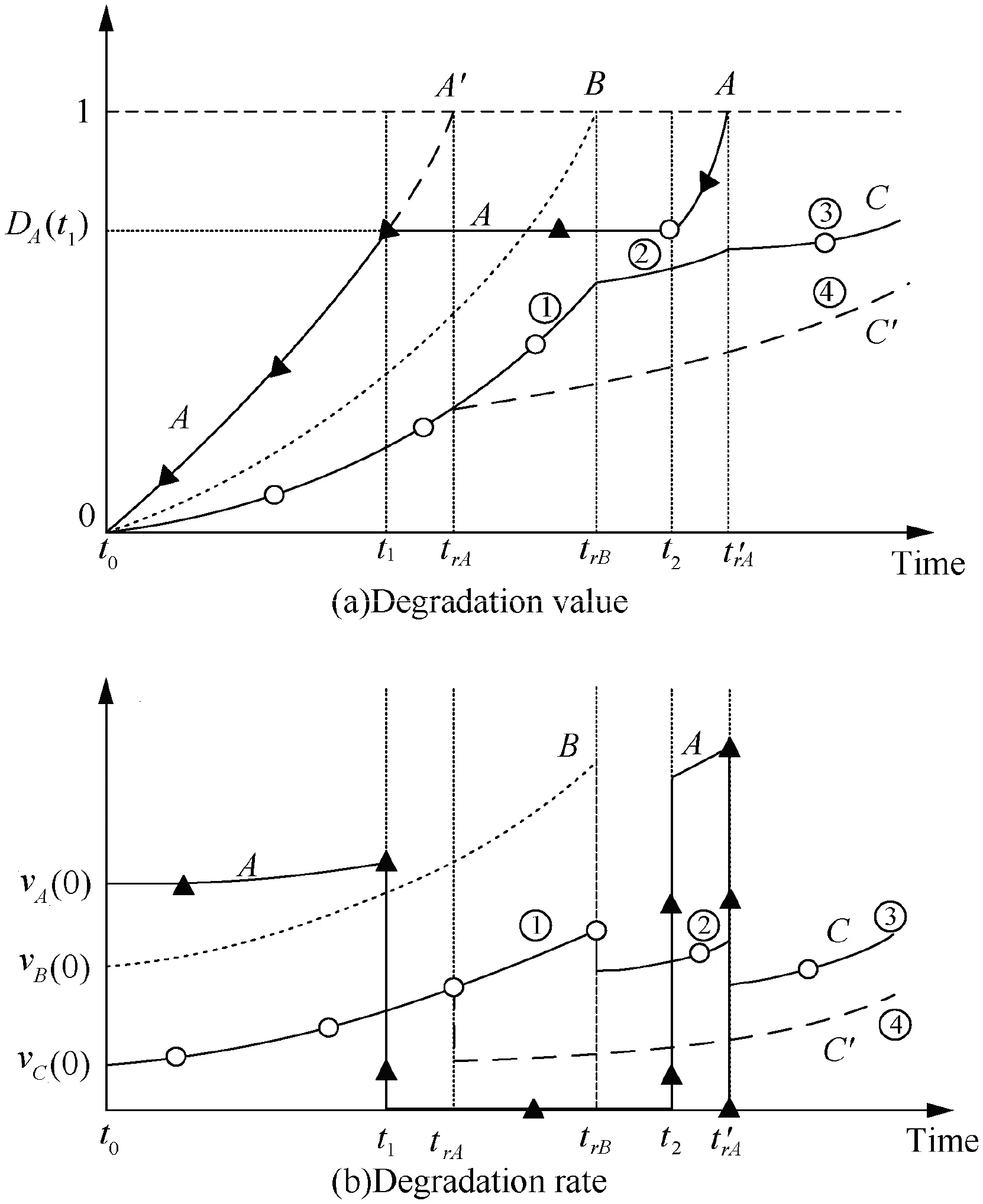
Fig.2 Degradation and degradation rate of A, B, C under certain conditions.

From this point of view,the phased changes in system configuration affect the failure sequence of components.With the change of mission phases,the coupling effect of the two dependencies on changes in system failure scenarios become complex and diverse.In actual engineering,the degradation process of each component is an uncertainty process,so the component failure sequence is not fixed,and the coupling effect between FDEP and PDEP has various influences on the failure behavior of the system,which causes the diversity of system failure modes.In a specific case,when the internal and external factors that affect the failure process are determined,which include the material,structure,and load conditions,the dynamic system failure behavior can be simulated.

3.Modeling and evaluation method

3.1.Stochastic degradation model

The degradation process of components can be described by the stochastic process under the influence of structure,material and environment condition.Here the positive drift wiener processis used to model the uncertain and dynamic degradation process(),where,

In whichis the initial value of()at the initial time;()is standard Brownian motion,()～(0，);μ is the drift coefficient,σ is the diffusion coefficient and does not change with load,and μ ＞0,σ ＞0.

In Eq.(1),μ determines the degradation rate of a component,which is a function related to environmental conditions and operation stress.Degradation of μ follows different forms under different environments and operation stresses.For example,when() is only related to temperature,the degradation follows the Arrhenius model,then,

whereis absolute temperature,is Boltzmann’s constant;is the activation energy,is a constant related to material and manufacturing process et al.

When a component degrades to the degree that it can’t meet the performance requirements,it will fail.Therefore the time to failure of the component tis the time when the value of the degradation function() reaches the threshold,which is assumed to be subjected to inverse Gaussian distribution,

Then the component failure Probability Density Function(PDF) is,

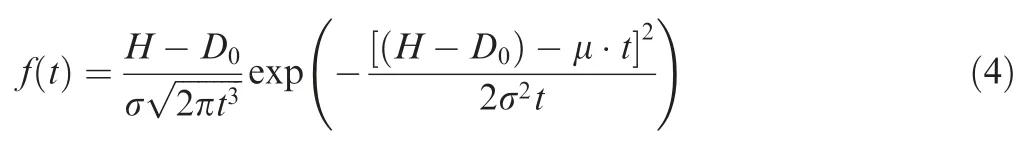
If the initial degradation is assumed to be zero,i.e.=0.The Cumulative Distribution Function (CDF) is,

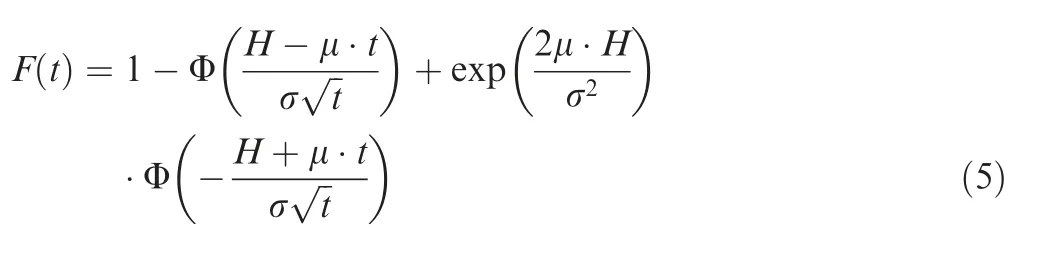
3.2.FDEP and PEDP in single phase system

Among them,σrepresents the diffusion coefficient in the process of accumulate degradation of component, His the degradation threshold of,μ () is the drift coefficient related to the ambient temperature,and:

It can be seen from Eq.(7)that Ais the frequency factor of,and its value is related to the structure and material of.is the activation energy of component.When t＜≤t,one of the componentsandfails,their PDEP effect disappeared.For the environmentally sensitive degradation process of,due to the change of external factors,the degradation rate ofwill be changed,the CDF ofat that time is,

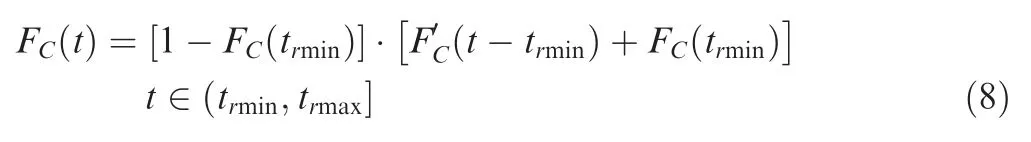
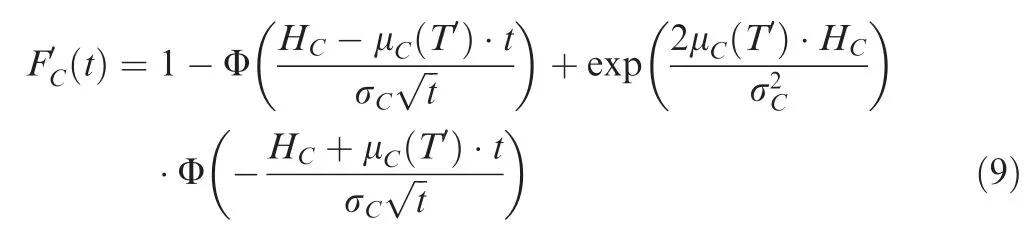
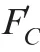
When considering FDEP betweenand,if t＞t,the CDF ofis as Eqs.(7)-(10),where t=t，t=t;if t≤t,after＞t= t,is isolated from the system due to’s failure,no longer has any PDEP impact on,the CDF ofwill be,

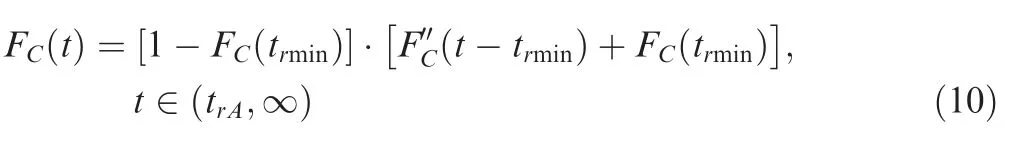
3.3.Modeling of the coupling effect in PMS

In PMS,when considering the FDEP and PDEP,the system failure CDF of each phase will change due to the different sequence of component failure.The detail conditions are discussed in phases as follows.

S

At timein the first mission phase,neithernorfails,and min(，t)＞，∈(，],which is recorded as event,then the occurrence probability ofis,

For the degradation process ofandthat are sensitive to the environment (such as temperature),there is,If at timein phase,fails,i.e.t＜，t＞t，∈(，],which is recorded as event,then the occurrence probability ofis,

If at timein phase,onlyfails,i.e.t＞，t＜，∈(，],which is recorded as event,then the occurrence probability ofis,

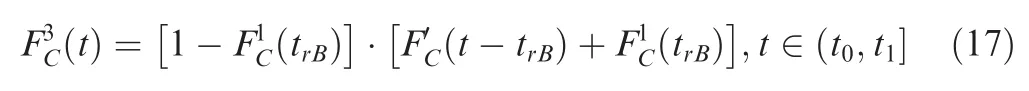
If at timein phase,bothandfail,and t＜t＜，∈(，],which is recorded as event,then the occurrence probability of this event is,

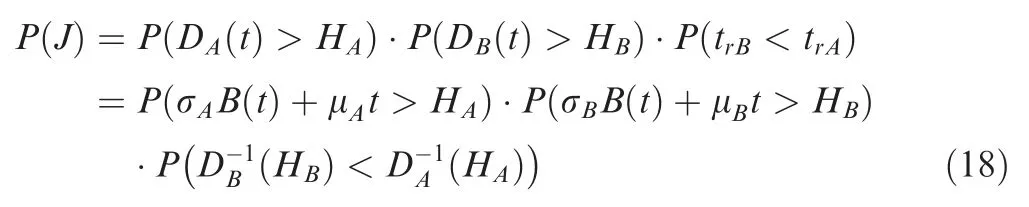
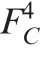
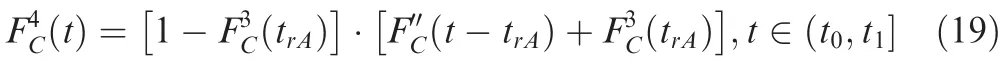
For a series system composed of componentsand,the CDF, F (),can be expressed by the function[F ()，F ()],where F ()，F () are the expressions for the CDF ofandunder current conditions,then,

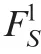
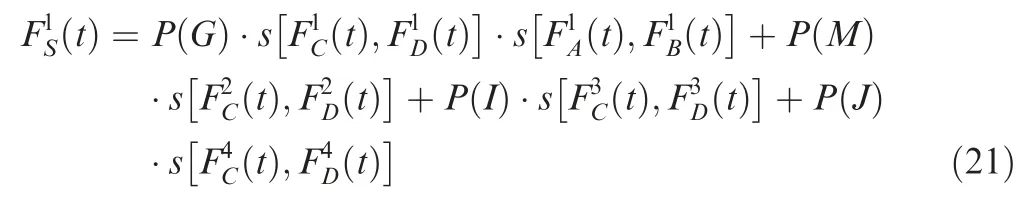
S

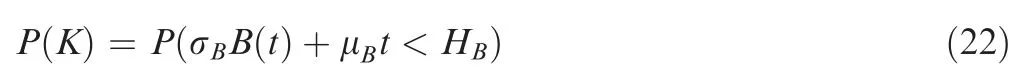
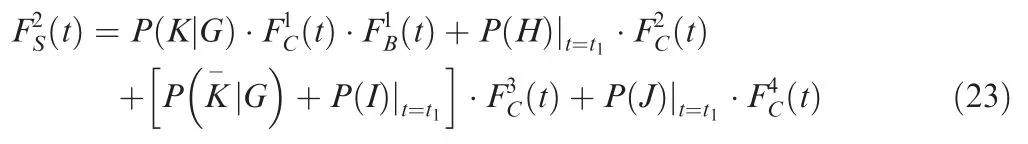
S

When the system enters phase,due to the change of the system configuration,,,andare all in the operational state,but due to the cross-phase dependence of the component status,the CDF of the system in this phase also depends on the status of each component in the previous phases.At time,ifdoes not fail,and recorded as event,then the occurrence probability ofis,

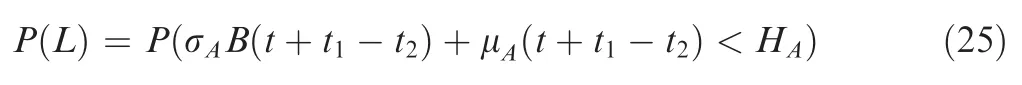
Sinceoperates in all phases,according to whetherfails or not,the CDF ofis as shown in Eq.(17) or Eq.(12).

Conversely,ifhas failed at time∈(，],and because the FDEP betweenand,iffails,it must precede’s failure.At this time,according to the different sequence of failures betweenand,the CDF ofis as shown in Eq.(15)or Eq.(19).Althoughdoes not operate in phase,due to PDEP,its CDF will still change after.

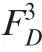
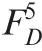
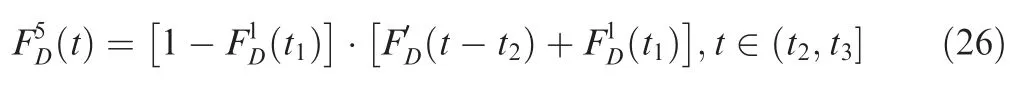
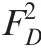
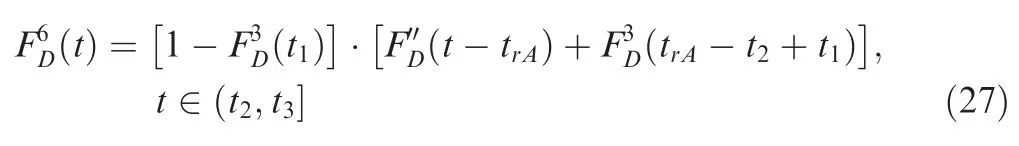
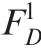
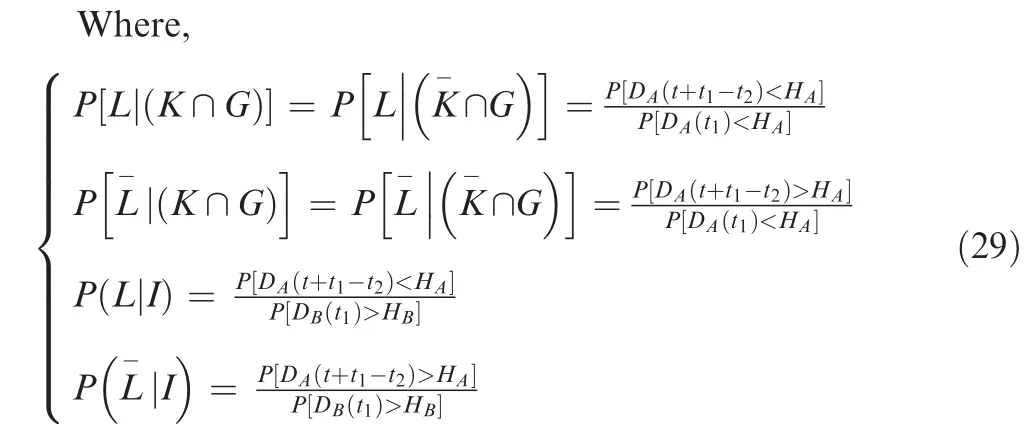
In summary,when considering PDEP and FDEP,the CDF of the system at any time in this PMS can be expressed as,

4.Case study

4.1.System description

Fig.3 shows the system configuration of an avionics controller system,which is a PMS with the aircraft’s take-off-cruiselanding process according to different mission requirements.The mission of the electronic controller includes three phases.For example,the ignition controller module that is in operational condition during the take-off phase is non-operational during the cruise phase.The working VDMOS module changes from one to two in the first phase and second phase.The number of resistors in the LDO module is also changed in different phases,etc.In addition,the modules and components also have cross-phase dependencies.

As shown in Fig.3,the coupling effect of FDEP and PDEP may have a new impact on the controller system.To describe this effect,a functional structure model of the main modules and components of the controller system is established.In each phase,the system can be regarded as a single-phase system affected by the previous phase.Therefore,in order to simplify the model,the description is still based on the relationship between the components of the aforementioned binary-state system.And the main modules in the system that are affected by FDEP and PDEP are replaced by components,,,and,whereandare the trigger components in PDEP,andare the corresponding dependent components;is the trigger component in FDEP,andis the corresponding dependent components.The configuration of the four components is the same as in Fig.1.

Fig.3 Controller PMS configuration.

Based on the degradation data of each component and the Probabilistic Physics-of-Failure(PPoF)method,the stochastic degradation process parameters of each component can be obtained as shown in Table 1.

4.2.Simulation algorithm

The main simulation algorithm is shown in Algorithm 1.Firstly,initialize the distribution parameter of the stochastic degradation process with the data from Table 1.Then,Sample the component failure time and return the result to the Algorithm 1.Compiling the algorithm in MATLAB,the total number of simulation cycles is 40000 and the total time spent in computing the reliability of componentsandand system on a typical personal computer (Dell Inspiron 14R-7420,i5-3230 M CPU 2.60 GHz) is 17 s.

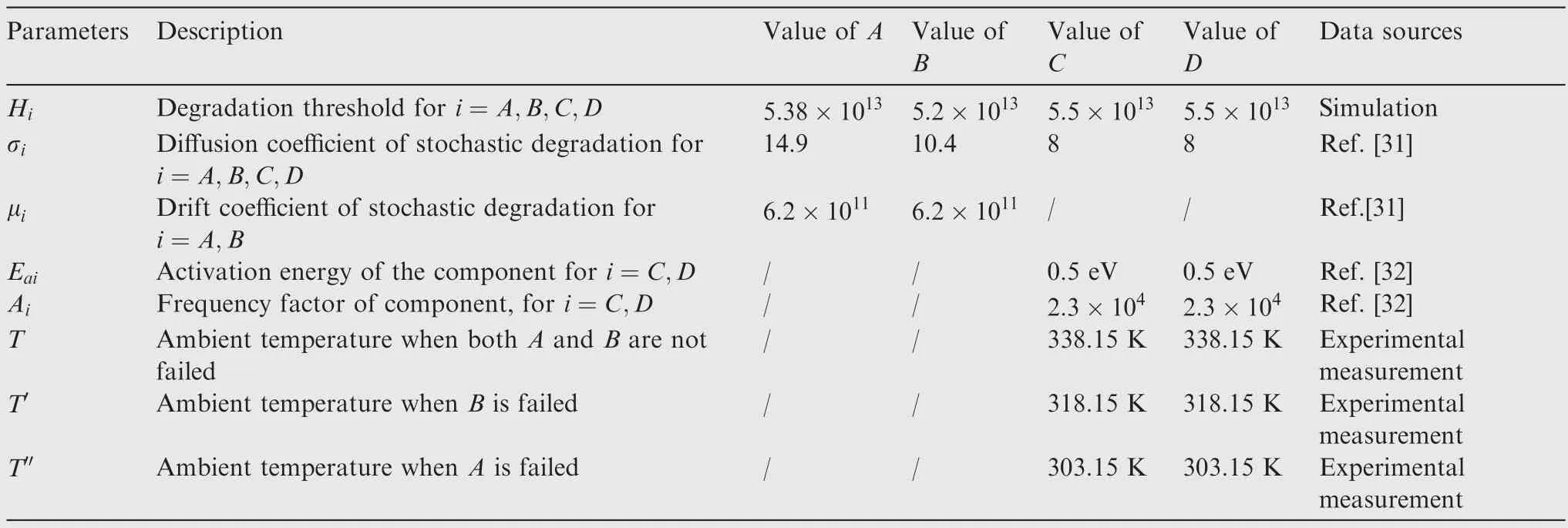
Table 1 Simulation parameters.

Algorithm 1 Main algorithm for the coupling effect model

4.3.Result and discussion

Based on the life time distribution of the functional trigger componentand the stochastic degradation process of the physical trigger component,the reliability curve of componentaffected by the PDEP is shown in Fig.4.In order to describe the effect of PDEP and FDEP onmore intuitively,Monte Carlo simulation method is used to obtain the reliability curve ofwhen only PDEP is considered in the system,and the condition when PDEP and FDEP are not considered.

It can be seen from Fig.4 that for componentthat is in operational state in all phases,its stochastic degradation process is not affected by the change of operational stress.When the FDEP between componentandand their PDEP effect onare not considered,the reliability curve ofis shown by the dotted line in the figure.When considering the coupling effect of PDEP and FDEP,which promotes the temperaturesensitive stochastic degradation process of,thus reducing the reliability ofwhenandare in operation state.Under this condition,the reliability curve ofis shown with the solid line in Fig.4.But the FDEP betweenandwill also affect the degradation process of.Whenfails,no matteroperate or not,it will be isolated from the system,sowill no longer be affected by the PDEP betweenand,the degradation rate ofwill decrease due to temperature changes.Therefore,when the FDEP in the system is not considered,the probability ofwill be increased,and its reliability will be reduced.The reliability results when only consider PDEP are more pessimistic.Besides,under the condition that only FDEP is considered,the life ofwill not affect the reliability ofor.Therefore,the reliability curve under this condition is not described in figure.

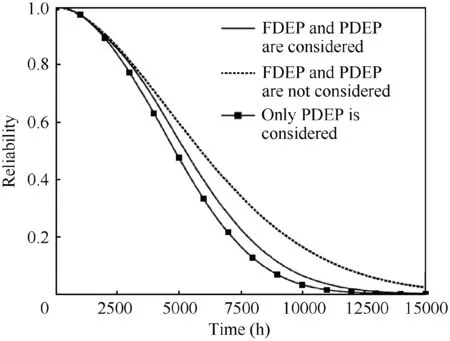
Fig.4 Reliability of C when considering the FDEP and PDEP or not.

As another component affected by the PDEP,is different fromin the configuration of each phase,and its reliability curve has many truing points,as shown in Fig.5.

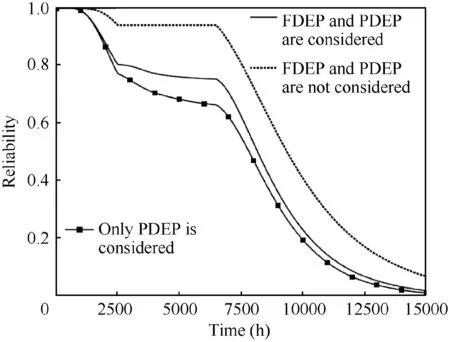
Fig.5 Reliability of D when considering FDEP and PDEP or not.

Although the degradation threshold of componentis same as,the life distribution ofis significantly different from that ofdue to the phased configuration.When the system enters phase,doesn’t operate,and its degradation is only affected by environmental factors.Therefore,when the PDEP and FDEP are not considered,the reliability curve ofis shown as the dotted line.As shown,the reliability ofremains unchanged in the second phase.When considering PDEP and FDEP in phase,the degradation ofis affected by the environmental temperature caused byand,and its reliability declines.When only the PDEP in the system is considered,will not terminate its PDEP ondue to’s failure.Therefore,under this condition,the reliability curve ofdrops more rapidly than the solid line.

The reliability function of the electronic controller system is shown in Fig.6.

It can be seen from Fig.6 that before and after=2500 h,whether the PDEP and FDEP are considered or not,the reliability of the system will undergo a turning point due to the change in the system configuration.The coupling effect and stress conditions affect the stochastic degradation rate.In addition,the reliability of the system considering the coupling effect of PDEP and FDEP is lower than that when PDEP and FDEP are not considered.The reason is that PDEP accelerates the stochastic degradation process of some components that sensitive to environmental condition.Due to the change of the system configuration,is in a non-operational state in the second phase,so in this phase,the inhibition of the FDEP on the PDEP is also reduced,and the development trend of the solid line after=2500 h is more similar as the change trend of reliability when only PDEP is considered.When FDEP is not considered,the PDEP will have a longer impact on the dependent component,so the reliability of the system is more pessimistic.

Fig.6 Reliability of case system when considering FDEP and PDEP or not.

4.4.Sensitivity analysis

Hrepresents the degradation threshold of the degradation of the component.Fig.7 shows the influence of the degradation threshold change on the reliability of the corresponding component,the failure time increases with the increase of H.At the same time,it is worth noting that when Hincreases,due to the increase in component failure time,as time goes by,the difference in reliability is more obvious when considering whether PDEP and FDEP or not.On the contrary,when Hdecreases,the component failure time is reduced accordingly,making the dependent components in PDEP more likely to fail before the trigger component failure.In other words,the time for the coupling effect of PDEP and FDEP to act on the componentis shortened.The gap between the solid line and the dotted line in Fig.7(c)is smaller than that in Fig.7(a).

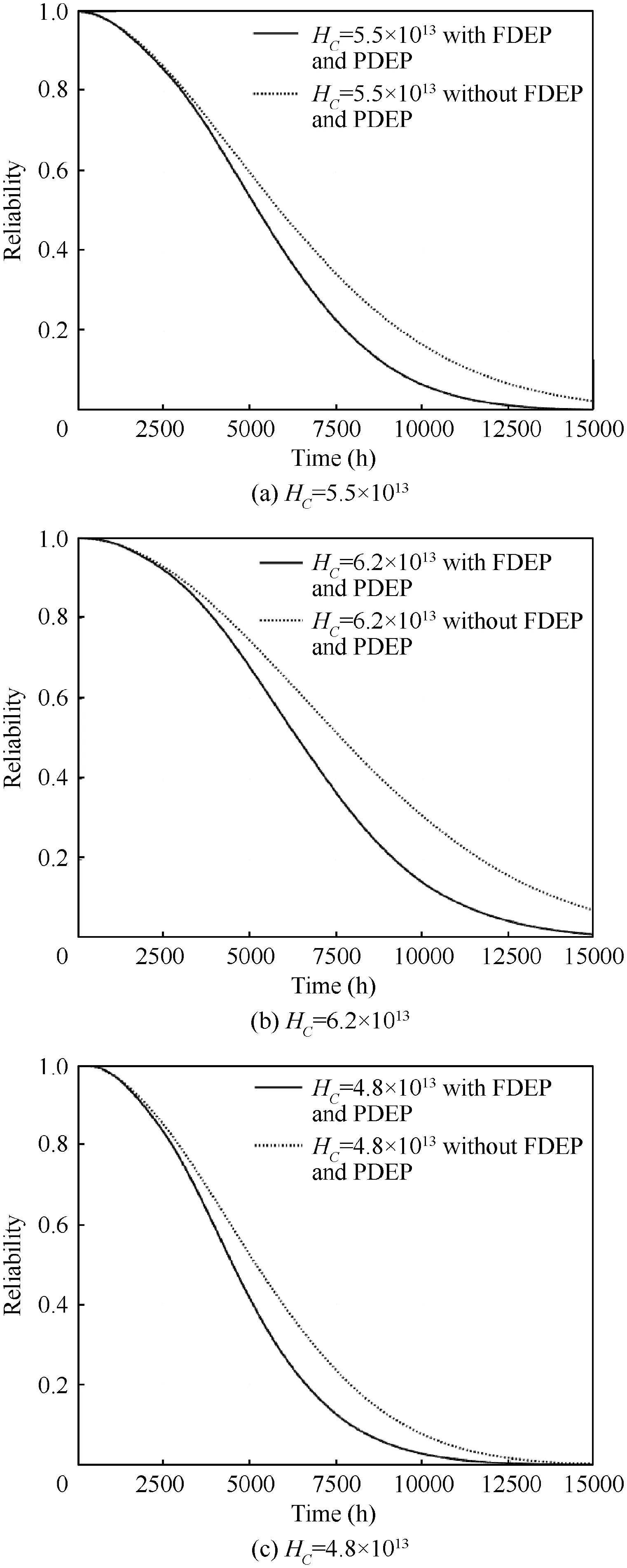
Fig.7 Effect of HC on the reliability of C.

is the operation environment temperature of component.According to Eq.(9) and Eq.(12),the operation environment temperature ofincludesaffected by the PDEP ofand,affected only by the PDEP ofandaffected byand.Fig.8 shows the influence of the physical trigger component on the degradation process of the dependent componentby the magnitude of the ambient temperature change.The dotted line shows the reliability curve ofwithout considering PDEP and FDEP.Under this condition,is always in operation at a fixed ambient temperature of 303.15 K.In contrast,it can be seen that when PDEP and FDEP are considered,if the physical trigger component has a small influence on the ambient temperature,the reliability curve ofis closer to the result when PDEP is not considered.As the influence of physical trigger components on the environmental temperature increases,the influence of PDEP on the reliability of dependent components increases.Whenandare large,the reliability curve ofdrops sharply.This is because high ambient temperature promotes the development rate of temperature-sensitive failure mechanisms in,and accelerates its degradation process.

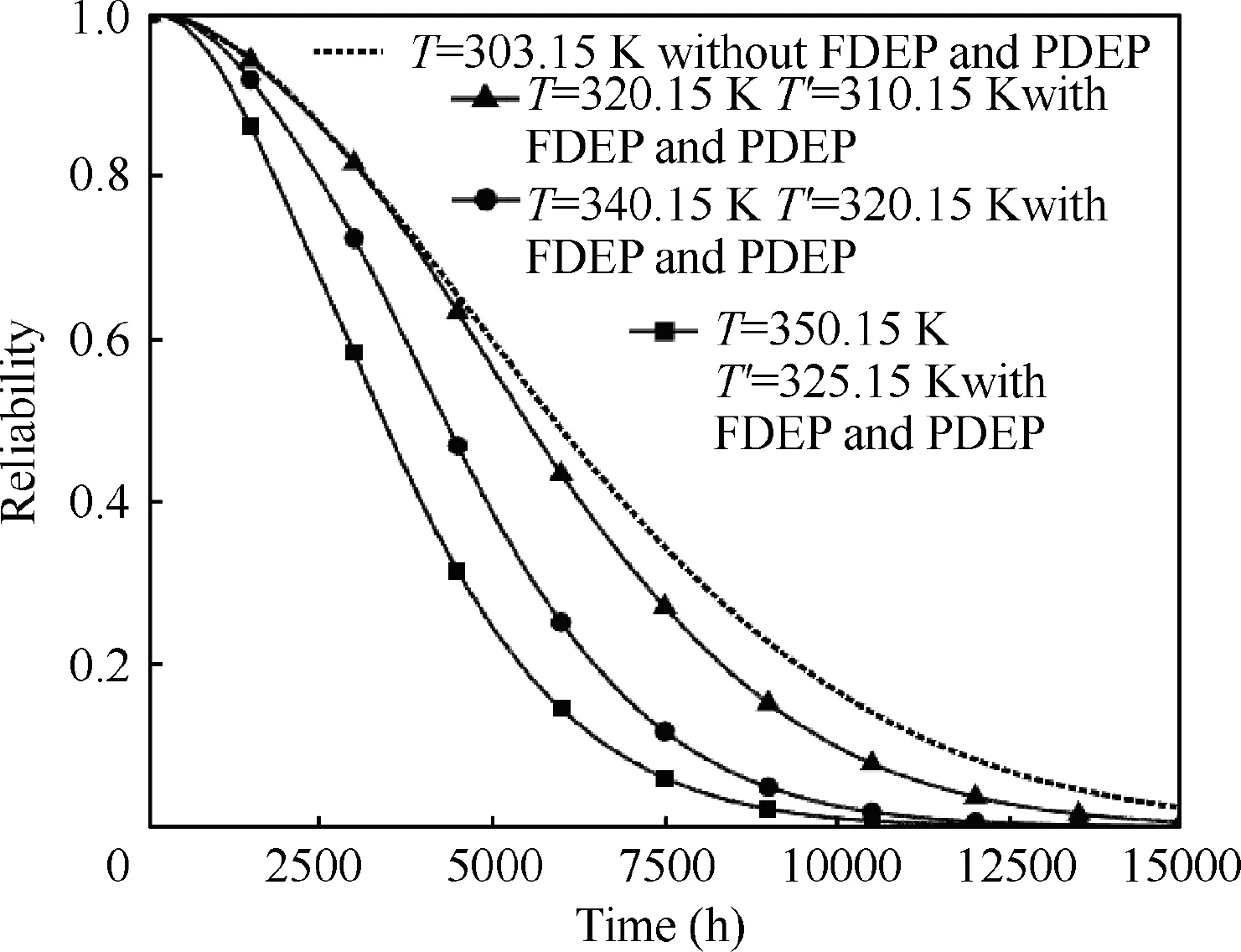
Fig.8 Effect of T on reliability of C.

5.Conclusions

The coupling effect of PDEP and FDEP in PMS are studied in this paper.A degradation time distribution model is presented for the coupling effect of the two kinds of dependencies.If the PDEP occurs,the stochastic degradation process of dependent components will be promoted with varying degrees.When FDEP occurs,the physical trigger components are isolated from the system,thus reducing the degradation rate of dependent components indirectly.Continuous stochastic process can be used to model the distributed trigger time.System reliability is obtained by considering total probability formula.

As a case,the coupling effect in an avionics controller system is studied.Reliability evaluation of this coupling effect shows that neglecting coupling effect will make the evaluation results too optimistic.By understanding the process of coupling effects on dependent components and the relationship between PDEP and FDEP,measures can be taken to eliminate the negative impact of the degradation process.

In the future,additional studies will be carried out to further improve the degradation time distribution model,since FDEP may not only have one-to-one or one-to-multiple relationship,system behavior may be different when multi components affect another group of components.Moreover,more environment conditions should be considered in PDEP.For more complex situations,the automatic generation and combination algorithms of failure scenarios should be studied to realize intelligent calculation of reliability.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was funded by the National Natural Science Foundation of China (No.61503014).