求解大型线性方程组的带动量贪婪随机Kaczmarz方法
王 雨 晴
(东华理工大学理学院,330013,南昌)
0 引言
机器学习、人工智能、信号处理和数据分析等众多工程应用中常常需要求解大型相容线性方程组
Ax=b,
(1)
其中系数矩阵A∈m×n,b∈m和未知向量x∈n。Kaczmarz方法[1]是求解大型线性方程组(1)的一个经典行启发式方法[2],该方法由Kaczmarz在1937年提出。Kaczmarz方法在理论、应用和算法推广都有很多进展,具体参阅文[3]及其参考文献。2009年,Strohmer和Vershynin[4]引入随机技术,提出了随机Kaczmarz(RK)方法,并证明RK方法具有线性收敛速率。此工作使得RK方法成为数值代数领域的研究热点。RK方法重新引起了人们对求解大型线性方程组(1)Kaczmarz类方法的兴趣,提出了很多改进方法,具体内容参阅文献[5-14]及其相关文献。最近,基于一种不同但更有效的概率准则,白和巫[15]提出了求解大型线性方程组(1)的贪婪随机Kaczmarz(GRK)方法。理论分析和数值结果表明,GRK方法的收敛速度快于RK方法。使用不同的概率准则,白和巫[16]建立了一类松弛贪婪随机Kaczmarz方法,张[17]发展了一个新的贪婪Kaczmarz方法。
Heavy-Ball型动量方法是加速梯度类型方法收敛速率的经典技术,该方法最早由Polyak[18]提出。众多研究人员对Heavy-Ball型动量方法进行了拓展研究,详见文献[19-20]。与Heavy-Ball型动量方法相比,Heavy-Ball型动量方法的随机变形在理论开发工作较少,例如在深度学习[21]中得到广泛应用的带动量随机梯度下降法(mSGD)。通过选择适当的sketch矩阵,RK方法可以看成SGD方法的一种特例[8]。受文献[18,22-23]的启发,本文结合随机逼近和Heavy-Ball型动量技术,构造了带动量的GRK方法(mGRK)。理论上证明了mGRK方法的全局线性收敛结果。数值实验进一步表明mGRK方法求解大型线性方程(1)时比GRK方法收敛性能更优。
本文结构安排如下:第1节建立mGRK方法并研究其线性收敛理论;第2节通过一些数值算例来验证mGRK方法的有效性;第3节总结全文。
1 带动量贪婪随机Kaczmarz方法
通过引入动量项γ(xk-xk-1),Polyak[18]提出了带有动量的梯度下降法(mGD),该方法也被称为Heavy-Ball型动量方法,即
xk+1=xk-αk∇f(xk)+γ(xk-xk-1),
(2)
其中αk和γ分别表示步长和动量权重系数,∇f(xk)表示目标函数的梯度。若令g表示梯度∇f(xk)的无偏估计量,则可得到带动量的随机梯度下降方法(mSGD)
xk+1=xk-αkg(xk)+γ(xk-xk-1)
(3)
选择适当的动量参数矩阵,mSGD方法可以退化为动量RK方法(mRK)。mRK方法的迭代形式为:
(4)
其中αk=1。
类似mRK方法,通过在GRK方法迭代步中嵌入动量项γ(xk-xk-1),建立了带动量的GRK方法(mGRK)。mGRK方法的伪代码见算法1。易知,当参数β=0时mGRK方法退化为GRK方法。
算法1:mGRK算法。
输入:A,b,l,x0,γ,fork=0,1,...,l-1do
计算:
(5)
确定指标集合:
(6)
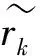

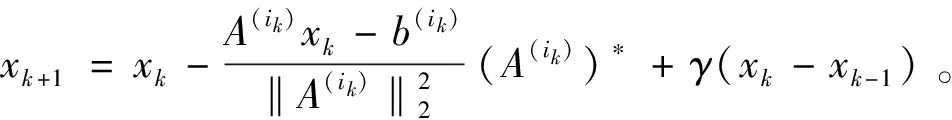
end for。
下面给出mGRK方法的全局线性收敛性理论。在建立定理1之前,首先描述如下2个引理。
引理1(文献[14]中的引理9):令F1=F0≥0,且非负实数序列{Fk}k≥0满足
Fk+1≤a1Fk+a2Fk-1,∀k≥1,
(7)
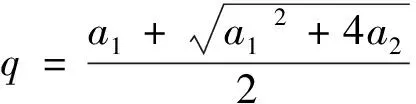
q≥a1+a2,
(8)
当且仅当a2=0(q=a1,δ=0)等号成立。
引理2:设a,b,c∈n,则下列等式恒成立
证明:经简单计算,易知
2〈a-c,c-b〉=2(a-c)*(c-b)=2a*c-2a*b+2c*b-2c*c
(9)
和
(10)
从而引理2得证。

(11)
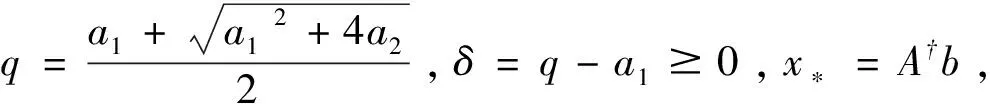
证明:由算法1的迭代步骤7可以得到
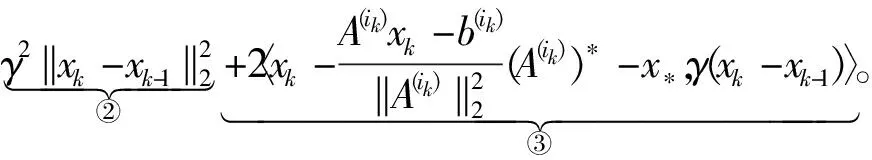
(12)
下面分别考虑①,②和③3个式子。从式子①中可得
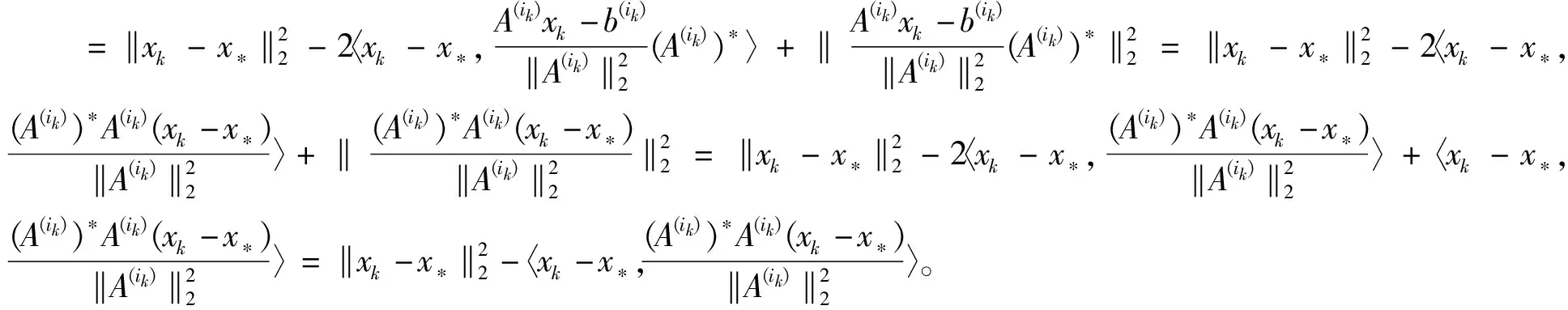
(13)
从式子③中可得
③
(14)
利用引理2,易计算
(15)
将式(15)代入式(14)中,可得
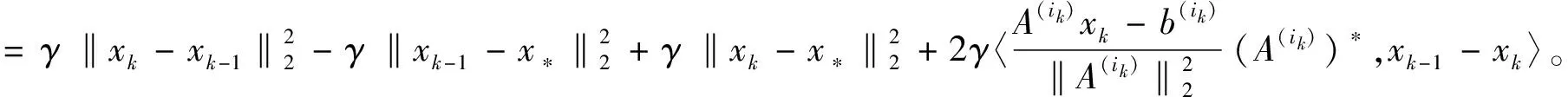
(16)
从式子②中,易推出
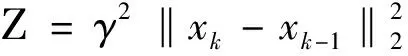
(17)
联合式(13)、式(14)和式(17),可得

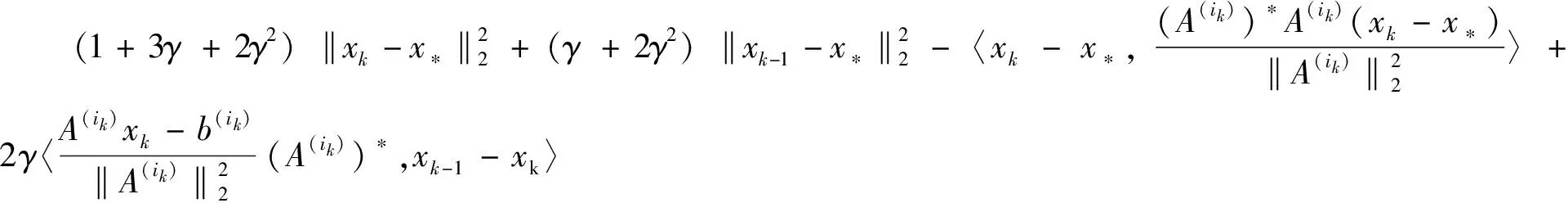
(18)
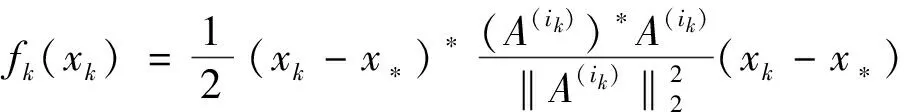
结合不等式(18),有

(19)
其中

经过简单计算,易得以下不等式
〈∇f(xk),xk-1-xk〉≤f(xk-1)-f(xk)。(20)
把式(20)代入式(19)可得

(21)
对f(xk)和f(xk-1),可得
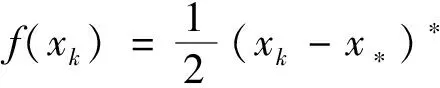
(22)
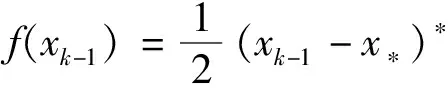
(23)
因此,联合式(22)和式(23),可得

(24)
Fk+1=a1Fk+a2Fk-1。
(25)
由式(24),易知a2≥0和a1+a2<1。故结合式(25)和引理1,可得
综上,定理1得证。
2 数值实验
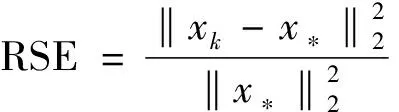
令右端向量b=Ax*,其中x*∈n由MATLAB函数randn随机生成。测试矩阵为高斯矩阵或从Tim Davis稀疏矩阵集[24]选择的实矩阵。设置中,mGRK方法中采用的动量参数β是通过实验找到的最小化迭代步数的参数。GRK方法相对mGRK方法的加速度定义为:
高斯矩阵由MATLAB函数randn随机生成,数值结果由表1和表2给出。
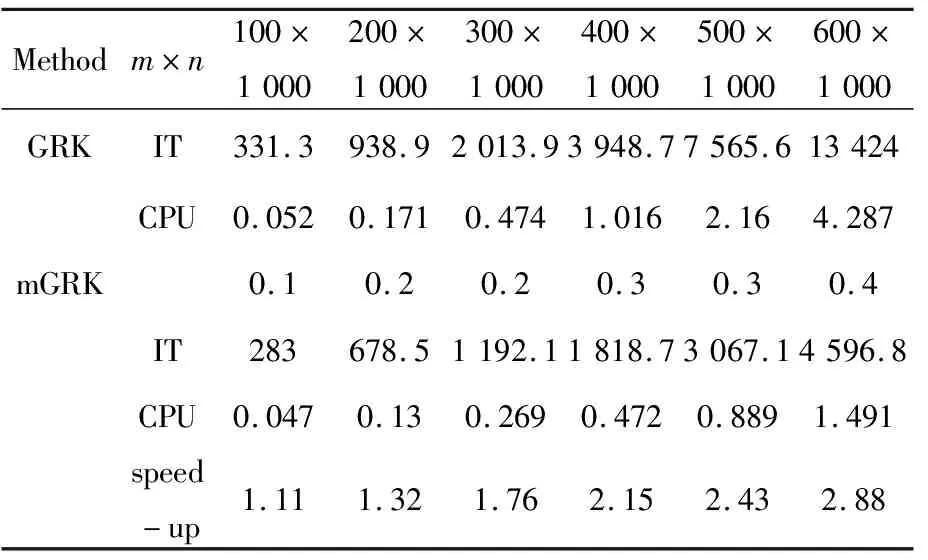
表1 A=randn(m,n)时,GRK方法和mGRK方法的数值实验结果

表2 A=rand(m,n)时,GRK方法和mGRK方法的数值实验结果
由表1和表2的数值结果,可得以下结论:1)GRK方法和mGRK方法求解相容线性方程组都是有效的;2)从迭代步骤和CPU时间看,mGRK方法均快于GRK方法,即增加动量项会给GRK方法的收敛特性带来有效的改进;3)当m 从Tim Davis稀疏矩阵集[24]选择12个具有代表性的系数矩阵,其矩阵性质见表3。相应数值结果见表4。 表3 12个实矩阵的性质 表4 A为实矩阵时,GRK方法和mGRK方法的数值实验结果 从表4中的实验结果可得GRK方法和mGRK方法呈现出与表1和表2中类似的数值结果。对矩阵Stranke94而言,mGRK方法在Speed-up方面取得最好的加速效果,加速值为6.75。除矩阵df2177、nemsafm、iiasa、Trec8和Stranke94外,在其他测试矩阵中动量参数β=0.3或β=0.4都是不错的选择。 本文提出了求解大型相容线性方程组(1)的带Heavy-Ball型动量的GRK方法,并研究了其收敛理论。数值结果表明,mGRK方法均优于GRK方法。针对实际问题,如何选择最优且实用的动量参数,将另文进行研究。 致谢:感谢张建华导师的悉心指导下完成了理论推导、数值实验等工作!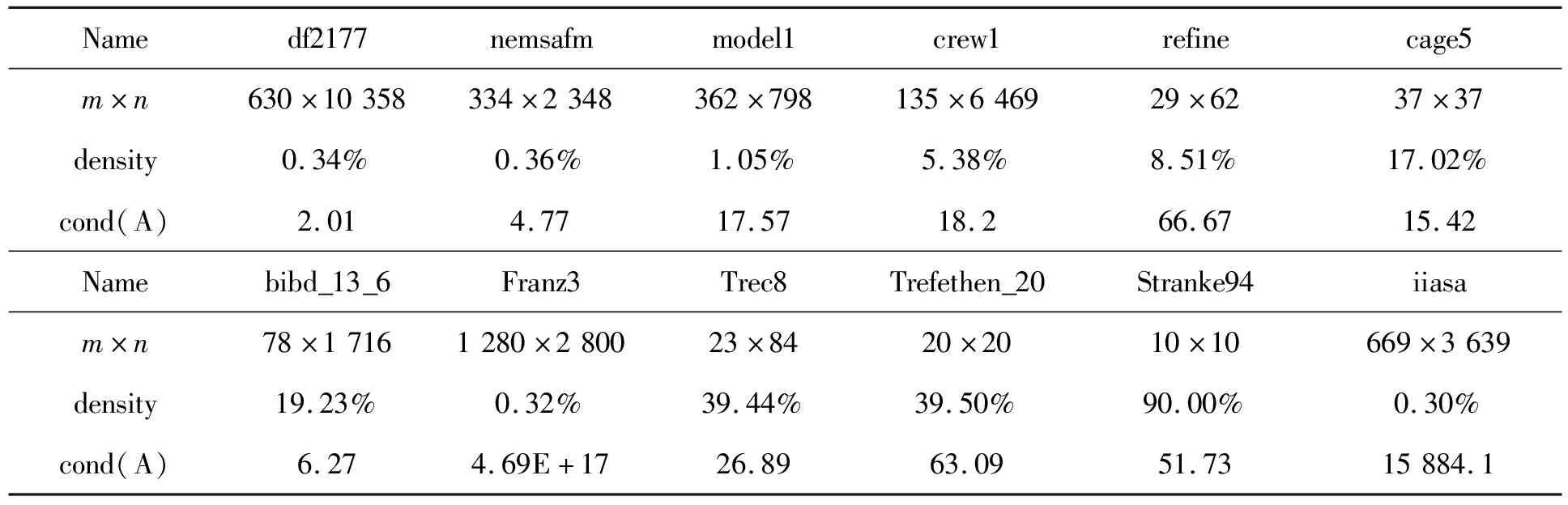

3 总结

