基于抗差LM的视觉惯性里程计与伪卫星混合高精度室内定位

杨高朝，王 庆，蔚保国，刘鹏飞，李 爽

1. 东南大学仪器科学与工程学院，江苏 南京 210096； 2. 东南大学智慧城市研究院，江苏 南京 210096； 3. 卫星导航系统与装备技术国家重点实验室，河北 石家庄 050050

视觉导航定位是通过视觉系统在相机运动过程中提取不同的图像，通过检测这些不同图像的变化，提取并且匹配相同的特征点，判断特征点的运动变化来估计相机的运动情况[1-3]。视觉里程计(VO)由于在面对单纯的旋转时无法很好地跟踪，因此在实际应用中通常会与低廉的IMU等惯性传感器进行组合，在组合后视觉惯性里程计(VIO)能够稳健地应用[4-5]。VIO虽然在光照条件、图像质量良好的情况下具有很高的定位精度，但在没有其他信息的情况下由于缺少全局的位置信息参考，其实质是一种局部定位算法，存在累积误差的问题[6]。因此，目前有许多研究通过设计全局的路标或者利用其他全局的信息予以补充，提高视觉定位在长距离范围的适用性。

VIO无法避免累积误差。GNSS是一种全局观测的传感器，每一次观测都是独立的，因此误差并不会累积，但是导航型GNSS定位输出频率和定位精度较低，通常无法满足用户更高的需求。从理论上看，将一个局部精度很高但存在累积误差的VIO和一个局部精度无法保证到不存在累积误差的GNSS相结合，可以互相弥补各自的不足[7]。

由于视觉、IMU等传感器无法获得全局信息，因此被定义为局部传感器。而对于GNSS、磁力计、UWB等能够感知全局信息的传感器，被定义为全局传感器。对于局部传感器，首先进行局部位姿估计，即传统意义上的VO或者VIO。得到局部的位姿估计之后，再与GNSS等全局传感器进行对齐。对齐的方式是建立一个位姿图，每个GNSS时刻建立一个位姿节点，连续的两个节点之间将局部位姿估计得到的相对位姿作为约束。每个节点还与GNSS等全局位置建立约束[8]。

文献[9—10]提出基于滤波的多传感器松耦合方法。主要思想是把IMU作为主传感器，通过积分得到6自由度的位姿。VO/VIO作为相对位姿的估计器，GNSS等作为全局位姿估计器，与IMU积分得到的结果进行EKF，得到更加准确的位置估计。IMU积分受到偏差和噪声的影响，会很快地发散。而VO可以认为在局部范围内误差很小，因此可以修正IMU的偏差。而GNSS不存在累积误差的问题，又可以修正IMU和VO/VIO的累积误差。GNSS的观测方程比较简单，即将待估计的位姿通过外参转化到GNSS坐标系的位姿，因为GNSS无法测量旋转，所以直接取三维位置的差作为观测误差。由于VO的尺度漂移是不稳定的，因此直接把VO的位姿放在全局坐标系下建立观测方程去估计尺度是不够准确的，因此，笔者提出了把VO的pose作为两帧之间相对的位姿去建立观测方程。

文献[11—12]提出基于优化的方式，支持双目配置、多轨迹融合以及GNSS等全局传感器与VO进行联合优化。

文献[11]主要思想是，首先进行局部位姿估计，即传统意义上的VO或者VIO，得到局部的位姿估计之后，再与GNSS等全局传感器进行对齐。对齐的方式是建立一个位姿图，每个GNSS时刻建立一个位姿节点，连续的两个节点之间将局部位姿估计得到的相对位姿作为约束。每个节点还与GNSS等全局位置建立约束。

文献[12]总体思想与文献[11]类似。但细节和试验上更加完备一些。笔者认为，GNSS无法提供旋转的约束，因此基于这种结构优化后的旋转的精度会变差。因此提出了第二种因子图结构。其中GNSS部分的约束保持不变。但相对位姿只利用VO/VIO的平移部分建立节点和节点之间的约束。而旋转则通过建立一个虚拟的局部坐标系，通过计算局部坐标系和全局坐标系(GNSS坐标系)之间的变换，建局部坐标系下的旋转转换成全局坐标系下的旋转，然后建立全局的旋转约束。在初始化阶段，通过直接对齐VO/VIO位姿和GNSS，解SVD来求解。在进行优化之前，笔者把VO/VIO的位姿与IMU进行一次松耦合的滤波。尽量减少与GNSS之间的时延带来的误差。

由于在室内无法接收到GNSS信号，因此在室内就无法利用GNSS消除VIO的累积误差。伪卫星又称“地面卫星”，是从地面某特定地点发射类似于GNSS的导航信号，采用的电文格式与GNSS基本一致。伪卫星系统作为GNSS定位系统的辅助手段和工具，即可以用来辅助增强GNSS在某些恶劣环境下的定位性能，也可以单独使用构建伪卫星定位系统。因此，在室内，可以利用伪卫星与视觉VIO进行组合消除VIO的误差累积[13]。但是伪卫星在室内应用中也面临着两大挑战。

伪卫星钟差的影响。由于GNSS中卫星钟差采用的是原子钟，精度较高，因此，在一般精度定位中可以忽略不计，但是原子钟价格昂贵，室内伪卫星采用不合适。由于伪卫星钟差的影响，单接收机无法完成定位，必须采用站间和星间双差技术，这在实际应用中非常不便。为了解决伪卫星钟差的问题，目前很多研究机构都是采用阵列天线来解决这个问题。阵列天线中所有的伪卫星钟差都是一样的，因此通过星间单差技术可以同时消去接收机钟差和伪卫星钟差[14-16]。

室内多径的影响。GNSS一般应用于室外定位，多径一般都忽略不计。但是室内结构复杂，多径对伪距的影响往往能达到几十米甚至几百米。而伪卫星通常是静止于室内的，无法通过多历元平滑来减弱多径。目前伪卫星多径解决方法主要分为3类：基带解调端、接收机端及数据处理端。因此，在实际室内应用中只利用载波观测值。由于只利用载波观测值会导致秩亏问题(N颗卫星至少需要解算(N+3)个参数)，为了解决这个问题，在动态应用前一般需要在已知位置上进行初始化一分钟[17-19]。

多传感器融合算法一般包括基于滤波和基于非线性的融合方式。基于滤波的算法有卡尔曼滤波(包括一些延伸的算法)、无迹卡尔曼滤波(UKF)及粒子滤波(PF)等，基于非线性优化的算法有最速下降法、高斯-牛顿及LM(Levenberg-Marquard)算法等[20-24]。很多文献表明，由于基于非线性优化的算法可以同时优化多个时间段的数据，因此基于非线性优化的算法要优于基于滤波的算法。本文主要研究基于非线性优化的融合算法。最速下降法无法确定收敛步长，步长较小会导致收敛较慢，步长较大会导致算法发散。高斯牛顿法采用二阶泰勒展开来近似，只有在展开点附近才会有比较好的近似效果，如果Hessian矩阵是非奇异矩阵，可能会导致算法发散。LM算法能够很好地克服上面的缺点，已经广泛应用于很多非线性优化实例中，但是LM算法还有自身的缺陷。尽管LM算法能够克服Hessian矩阵病态解的影响，由于LM算法采用最小二乘估计作为收敛条件从而不能抵御传感器数据中心粗差的干扰，特别是室内伪卫星定位时，由于室内多径比较严重，很难保证伪卫星定位的稳定性和可靠性。若直接使用LM算法进行优化，则会使得求解出的融合解偏离真实值。鉴于VIO和伪卫星单独定位的缺陷，本文主要研究应用抗差LM算法进行VIO和伪卫星融合的问题。

1 多源数据融合约束方程的建立

1.1 数据内插

多传感器的融合时间戳对齐是非常关键的一步。时间戳无法对齐或对齐错误最后可能得出一个错误的轨迹，很可能使优化算法失效。为了保证融合算法的稳健性，视觉传感器的时间戳与伪卫星的时间戳相差不超过10 ms。

一般伪卫星数据的输出频率为1～5 Hz，而视觉VIO数据一般可以达到10～20 Hz，为了更方便进行后端融合，本文首先根据视觉输出的频率及相应的时间戳对伪卫星输出数据进行内插。由于两个伪卫星输出数据间隔一般只有3～4个视觉输出数据，考虑到内插平滑的精度，本文利用三次样条曲线内插[25]，假设已知的n个坐标点(S(ti),ti)，…，(S(ti+n),ti+n)，其中S(ti)为ti时间戳对应的三维坐标值x(ti)，y(ti)和z(ti)，本文可以列出样条曲线的微分式。如果函数S(ti)满足以下3个条件(本文为了方便计算，把xi,yi,zi根据ti分开内插求解)：

(1)S(ti)=x(ti),i=(1,2,…,n)。

(2)S(ti)在每个区间上[ti,ti+1](1,2,…,n-1)是一个三次多项式。

(3)S(ti)在整个区间上[t1,tn]有连续的一阶及二阶导数。

则称S(ti)为过n个点的三次样条函数。三次样条曲线内插是通过一系列形值点的一条光滑曲线，数学上通过求解三弯矩方程组得出曲线函数组的过程。实际计算时还需要引入边界条件才能完成计算。假设方程为

Si(t)=ai+bi(t-ti)+ci(t-ti)2+di(t-ti)3
i=1,2,…,n-1

(1)

1.2 多传感器约束方程的建立

为了实时进行伪卫星和VIO的融合，本文选择滑窗融合模式，窗口长度为10。伪卫星坐标系采用室内局部坐标系。为防止秩亏现象发生，首先把融合后的地图坐标系第一帧与伪卫星坐标系对齐。

由于伪卫星不能求出旋转向量，因此在优化的时候只能利用坐标向量和速度向量。总的融合约束方程可以写为

(2)

χ=[pi,Gqi,GVi,Gbi,gbi,api,CGqi,CG]

(3)

式中，pi,G、Vi,G和qi,G是优化后的全局平移、速度和旋转参数；bi,g和bi,a分别是陀螺仪和加速度计偏置；i表示滑动窗口中帧数；C、S和G代表视觉世界、伪卫星和融合后全局坐标系标志。

由于pi,CG、qi,CG和视觉VIO密切相关，而视觉VIO会随着时间有误差累积，因此,pi,CG和qi,CG也会有误差累积。为了使优化后的位姿更加平滑，本次研究选择实时优化这两个向量。

1.2.1VIO约束

由于VIO的尺度漂移是不稳定的，直接把VIO的位姿放在全局坐标系下建立观测方程去估计尺度是不够准确的，因此，把VIO的两帧之间相对的位姿去建立观测方程

(4)

(5)

(6)

视觉目标函数可写为

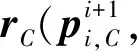
(7)

1.2.2 伪卫星约束

伪卫星约束计算公式为

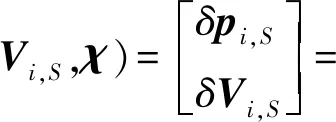
(8)

(9)

δVi,S关于pi,G、θi,G、Vi,G、bi,g和bi,a的雅克比矩阵为

(10)

1.2.3 基于扩展卡尔曼滤波的全局坐标初始化

pk,G和qk,G为全局坐标系下的平移和旋转矩阵。由于伪卫星只能提供全局位置和速度约束，因此若想求得当前坐标系相对全局坐标系下的旋转矩阵，至少需要提供4个历元的位置约束。假设滑窗宽度为10，首先利用扩展卡尔曼滤波初始化全局坐标。

状态预测方程为

(11)

状态更新方程为

(12)

当i=1时

p1,G=p1,S

(13)

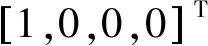
(14)

V1,G=V1,S

(15)

假设i是当前帧，根据pi,C、qi,C、pi,G及qi,G，可以求得视觉世界坐标系到全局坐标系的旋转和平移矩阵pi,CG和qi,CG为

(16)

(17)

(18)

由于VIO随着时间误差会累积，因此，为了更加准确地求取视觉世界坐标系到全局坐标系的转换，在每次优化完成后重新求取pi,CG和qi,CG。

1.3 有效性检核

为增加定位的稳健性，减少粗差给融合定位带来影响，本文使用下列方案检验数据的有效性。

已知第i+1帧相对视觉世界坐标系(视觉初始化时的参考坐标系)下的平移量pi+1,C，又已知第i帧视觉世界坐标系向全局坐标系的旋转矩阵qi,CG和平移矩阵pi,CG，可以得到第i+1帧全局坐标系下的坐标估值为

(19)

假设伪卫星在i+1时刻的坐标为pi+1,S，方差为σ2，可以建立检核方程为

(20)

2 改进的抗差LM非线性优化的融合策略

已知LM非线性优化模型为

(Hk+μkI)Δxk=gk

(21)

采用拉格朗日乘子将上述问题转化为一个无约束问题

(22)

因此，LM算法可以看作给变化量Δx添加一个信赖区域来限制Δx的大小，并认为在信赖区域里面近似是有效的，否则近似不准确。

确定信赖区域一个好的办法是通过比较近似模型和实际模型的差异来确定，如果差异小，就增大范围；如果差异太大，就缩小范围。考虑实际模型和近似模型变化量的比值

ρ=(f(x+Δx)-f(x))/(J(x)Δx)

(23)

式(23)可以通过ρ的值来判断泰勒近似的好坏，其中分子是实际模型的变化量，分母是近似模型的变化量。当ρ接近1的时候，表明近似模型较好；如果ρ较小，则实际模型的变化量小于近似模型的变化量，则认为近似模型较差，需要缩小近似范围。反之，当ρ较大时，说明实际模型变化量更大，需要放大近似范围。经典LM算法可以表示如下：

(1) 给定初始迭代值x0(坐标向量初值可由伪卫星给出，旋转向量初值由视觉VIO提供)及调节因子μ0：μ0=max([hii])，其中hii是H0的对角线元素。

(2) 对于第k次迭代，求解优化问题。

(3) 计算ρ。如果ρ>0，则认为近似可行，令xk+1=xk+Δxk；若ρ>4/5,则μk+1=2μk；若ρ>1/5，则μk+1=0.5μk。

(4) 判断算法是否收敛。如果不收敛，跳回步骤(2)，否则结束。

当μk较小时，说明Hk占主导地位，说明二次近似在该范围内是比较好的，LM方法更接近于高斯牛顿法；另一方面，当μk较大时，LM算法更接近一阶梯度下降算法，这说明二次近似不够好。LM算法的求解方式，可以避免线性方程组的矩阵非奇异和病态等问题，提供更稳定、更准确的解法。

(Hk+μk·diag[Hk])Δxk=gk

(24)

diag[Hk]指只保留Hk的对角线元素。带上矩阵diag[Hk]后约束区域就是一个椭球，可以约束参数中不同维度的变化。

尽管LM能够克服Hessian矩阵病态解的影响，由于LM算法采用最小二乘估计作为收敛条件从而不能抵御观测数据中心粗差的干扰，特别是室内伪卫星定位时，由于室内多径比较严重，即使伪卫星原始观测数据能够通过上文的有效性检核，仍旧很难保证伪卫星定位的稳定性和可靠性。若直接使用LM算法进行优化，则会使得求解出的融合解偏离真实值。

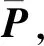
(25)

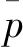
本次研究的多传感器融合具体流程如图1所示，本文主要研究基于抗差LM优化的VIO与伪卫星后端松耦合技术。下面主要通过试验对比来分析融合的优势。

图1 多传感器融合流程Fig.1 Flowchart of multi-sensor fusion

3 试验验证及分析

3.1 试验验证

为了验证本文提出的多传感器融合算法，本文利用笔者团队搭建的组合设备在某所C7试验场进行测试。图2(a)多传感器融合实时测试设备；图2(b)是试验场景图，图2(a)中的箭头所指的区域为伪卫星信号发射系统，试验场地一共有8颗伪卫星，为了消除伪卫星钟差，使用了阵列天线，由图2可以看出，伪卫星结构分布较差，且都分布在房屋顶部；图2(b)中的箭头所指的区域为光电捕捉系统设备，试验场所二楼一周都布满了该设备，长和宽大约都是20 m。本研究利用光电捕捉设备测量的数据作为真值进行参考，视觉定位部分采用小觅双目相机标准版。为了验证本文提出的融合算法，使用搭建的测试设备分别采集两组场景数据(长度分别为41 m和271 m)进行对比分析。绝对轨迹误差(ATE)直接计算相机位姿的真实值与系统的估计值之间的差，首先根据位姿的时间戳将真实值和估计值进行对齐，然后计算每对位姿之间的差值，该标准适合于估计系统的漂移。

图2 多传感器融合设备和伪卫星分布Fig.2 Multi-sensor fusion equipment and pseudosatellite map

3.2 结果分析

3.2.1 伪卫星定位性能分析

PDOP(position ditution of precision)大小能够反映伪卫星结构的好坏，PDOP越小，结构越好。图3是室内试验场地伪卫星PDOP分布。可以看出，越往四周PDOP越差，中间区域结构最好。图4(a)和4(b)是场景1伪卫星定位轨迹对比图和定位残差图；图5(a)和5(b)是场景2伪卫星定位轨迹对比图和定位残差图，真值为光电捕捉数据。伪卫星实时坐标解算采用星间单差的模式，由于在伪卫星发射系统中采用了阵列天线，因此，星间单差能够同时消除伪卫星钟差和接收机钟差。由图4可以看出，尽管伪卫星数据不平滑，噪声较大，但残差较为均匀，基本都在0.5 m之内。由图4和图5对比可知，由于场景2测试范围较大，从图3可知PDOP因子较差，因此场景2的伪卫星定位精度比场景1定位精度差。

图3 室内伪卫星PDOP分布图Fig.3 PDOP distribution map of indoor pseudosatellite

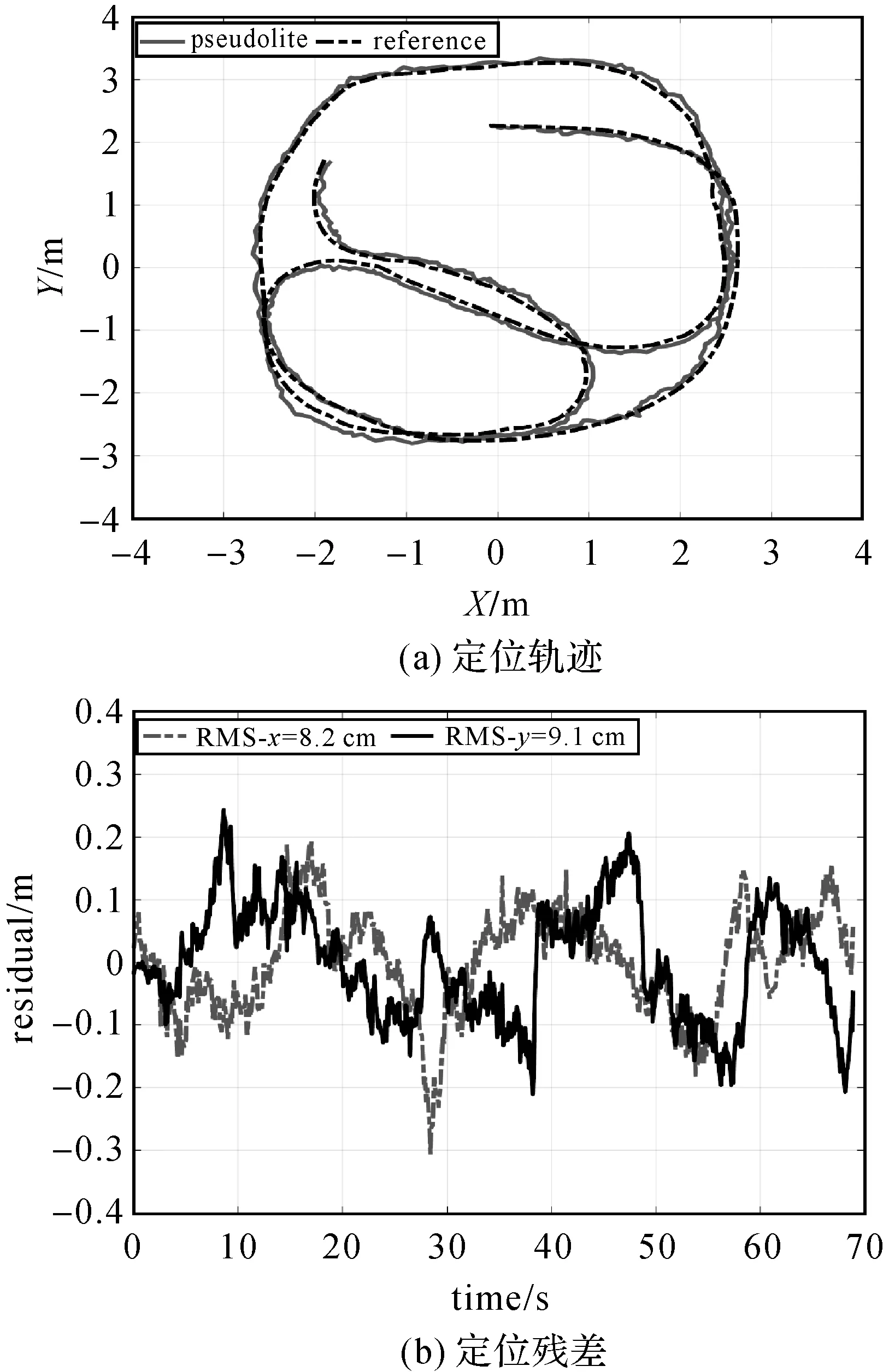
图4 场景1中伪卫星定位效果Fig.4 Pseudosatellite positioning result in scene 1

图5 场景2中伪卫星定位效果Fig.5 Pseudosatellite positioning result in scene 2

3.2.2 视觉定位性能分析

图6是视觉VIO试验场景图。图7(a)和7(b)分别是场景1的VIO定位轨迹对比图和VIO定位残差图；图8(a)和8(b)分别是场景2的VIO定位轨迹对比图和VIO定位残差图。由图7和图8以看出，虽然VIO数据较为平滑，但RMS不均匀，波动较大，特别是场景2，最大误差达到2.5 m。

图6 VIO试验场景Fig.6 VIO experimental scene diagram

图7 场景1中VIO定位效果Fig.7 VIO positioning result in scene 1

视觉里程计定位性能受环境因素和运动状态影响比较大。在强光环境下或者运动状态剧烈的时候会导致误差累积越来越大，甚至会直接使里程计挂掉。

由图4—图8可知，尽管伪卫星实时定位噪声较大，但是误差不会像视觉里程计那样有累积，绝对误差的波动幅度会保持在一个相对大小的值。视觉误差尽管会随着距离的增加误差会渐渐累积，但是在短时间内会保持在一个极小的值。因此，二者可以实现优势互补。下文就二者的组合定位性能进行分析。

图8 场景2中VIO定位效果Fig.8 VIO positioning result in scene 2

3.2.3 组合定位性能分析

本文主要研究应用抗差LM算法进行VIO和伪卫星融合的问题。为了对比本文算法的性能，下文主要利用经典的LM算法优化后的效果与本文算法优化后的效果及进行对比分析。

图9和图10是视觉世界坐标系与全局坐标系的旋转和平移图，可以通过式(26)求解

(26)

式中，pi,G和qi,G分别是优化后全局坐标系下的平移和旋转矩阵；pi,C和qi,C是利用视觉惯性里程计输出的在视觉世界坐标系下的平移和旋转矩阵；i指当前最新帧。求解qi,CG和pi,CG的目的是为i+1帧全局坐标系旋转和平移矩阵提供一个初值。

由于两个坐标系都属于参考坐标系，原则上两个坐标系的平移和旋转矩阵应该是固定的。但由于VIO存在误差累积的因素，不同时刻两个坐标系的旋转和平移是发生变化的，每个时间段的视觉世界坐标系和全局坐标系之间的旋转和平移矩阵也会发生变化，因此视觉世界坐标系和全局坐标系之间的平移向量的波动较大并不完全等同于系统融合后的定位残差。由于在测试场地非常整平，因此平移转换时暂不考虑高程的变化。由图9和图10可知，全局与视觉坐标系之间平移向量X和Y方向的波动几乎在2 m左右。图9和图10下半部分是3个旋转欧拉角变化图。由图中可知，除了yaw波动较大外，pitch角和roll角相对都比较稳定。这是由于pitch和roll可以通过校准后的重力方向进行纠正，方向是可观的，而yaw方向无法纠正，因此，yaw角会随着时间误差累积越来越大。

图9 场景1中视觉世界坐标系与全局坐标系的平移和旋转Fig.9 The translation and rotation of the visual world coordinate system and the global coordinate system in scene 1

图10 场景2中视觉世界坐标系与全局坐标系的平移和旋转Fig.10 The translation and rotation of the visual world coordinate system and the global coordinate system in scene 2

图11是场景1中经典LM 融合定位效果，图12是场景1中抗差LM 融合后定位效果，图13是场景2中经典LM 融合后定位效果，图14是场景2中抗差LM 融合后定位效果。“RMS-xy”代表平面的绝对误差大小。由图11和图12可知，经典的LM算法融合后，X和Y残差的最大值都达到了0.2 m，而利用改进的LM算法融合后最大只有0.15 m。表1是场景1和场景2关于4种定位方案的RMS对比，表中最后两列分别表示经过LM融合后平面方向精度相对于伪卫星和VIO提高的百分比(计算方式为：百分比=(A-B)/A，其中，A为改进前的RMSE，B为改进后的RMSE)。由表1可知利用改进的LM算法融合后场景1相对于伪卫星和VIO定位精度分别提高了35.5%和59.0%；场景2相对于伪卫星和VIO定位精度分别提高了27.8%和77.5%。通过对比场景1和场景2相对于VIO精度的增长率可知：轨迹越长，VIO的误差累积越大，组合系统相对于单系统VIO的优势越明显。组合系统能有效消除VIO的误差累积。

图11 场景1中经典LM融合定位效果Fig.11 Positioning result after classic LM fusion in scene 1

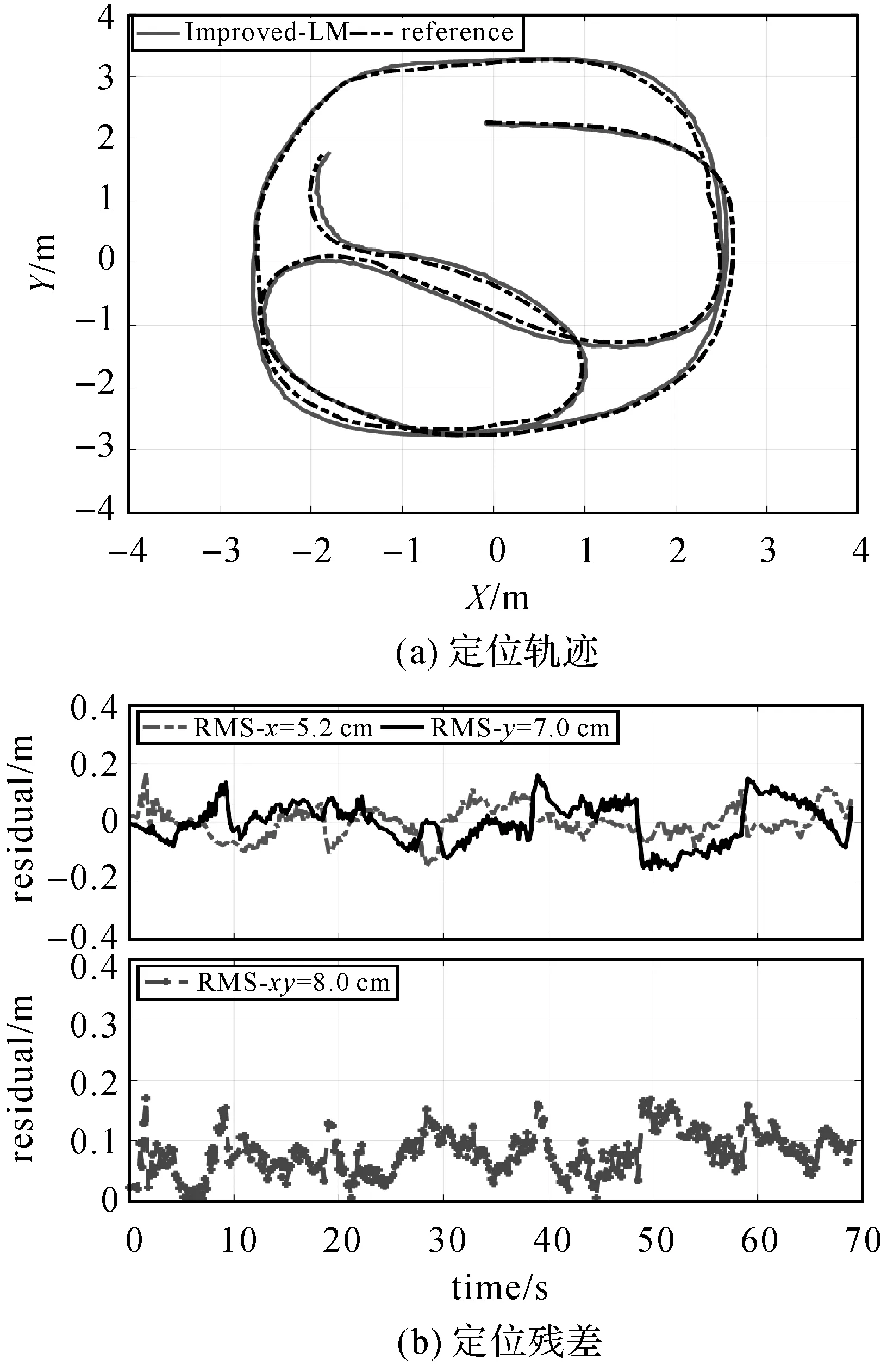
图12 场景1中抗差LM融合后定位效果Fig.12 Positioning result after classic LM fusion in scene 1

图13 场景2中经典LM融合后定位效果Fig.13 Positioning result after classic LM fusion in scene 2

图14 场景2中抗差LM融合后定位效果Fig.14 Positioning result after robust LM fusion in scene 2

表1 不同传感器组合方案平均定位精度对比Tab.1 Comparison of average positioning accuracy of different sensor combination schemes

3.2.4 遮挡下组合定位分析

由于VIO是VO与IMU采用紧组合建模，视觉在短时间内具备较高的相对定位精度，因此，IMU的加速度计偏差和陀螺仪偏差在短时间内能够通过VO进行修正，因此，VIO在短时间内能够得到较为平滑的高精度定位数据。为了验证伪卫星在遮挡下组合系统中定位系统定位的性能，本试验场景1在12～17 s及29～34 s两个时段给伪卫星设置全遮挡；场景2在35～65 s及85～135 s两个时段给伪卫星设置全遮挡；在135～185 s时间段给伪卫星设置半遮挡(即在试验中有1～3颗卫星被遮挡。由于伪卫星发射器利用了阵列天线，利用星间单差就可以基本消除伪卫星钟差和接收机钟差，因此4颗卫星就可以完成定位)。

图15(a)和图16(a)是伪卫星存在短时间遮挡下与视觉VIO组合定位轨迹图，图15(b)是场景1定位残差图，16(b)是场景2可用伪卫星数及定位残差图。由图15(b)可以看出，场景1的最大残差不超过0.2 m，除了在30 s和50 s处有较小的波动外，其余部分都非常稳定；场景2的残差波动较大，但整体都在1 m之内。场景2的遮挡分为全遮挡和半遮挡。由图中可以看出，当可用伪卫星个数满足定位要求时，组合定位性能基本不受影响。结合图2和图3通过分析可知，由于伪卫星都分布在试验场顶部，而且伪卫星都是静止不动的，PDOP较差，因此在满足定位要求后，伪卫星的个数对定位结果影响较小。可知，即使伪卫星在短暂遮挡下，基本不影响组合系统定位性能，组合系统依然能够输出较高精度定位数据。

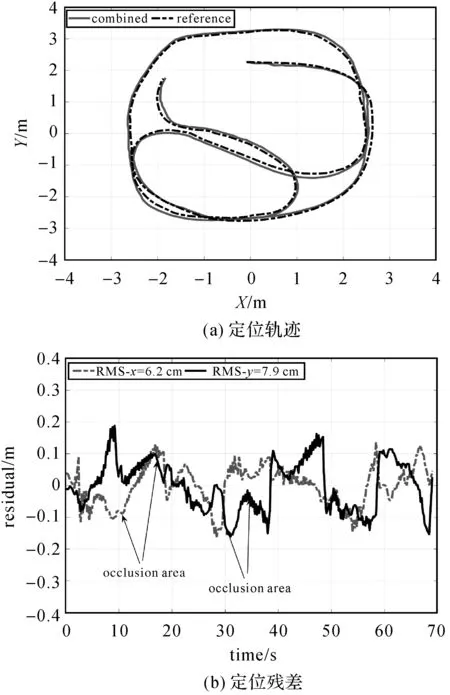
图15 场景1中VIO遮挡下定位效果图Fig.15 Positioning result under VIO occlusion in scene 1

图16 场景2中VIO遮挡下定位效果图Fig.16 Positioning result under VIO occlusion in scene 2

图17分别是不同频率(5、1和0.2 Hz)的伪卫星输出结果与视觉惯性里程计组合后的定位轨迹和定位残差图，平均定位残差分别是0.254、0.278、0.312 m。经过分析可知，伪卫星的频率越高，内插精度也就越高，因此能更精确地修正陀螺仪和加速度计的偏差，组合后的精度也就更高。由于在室内多径现象比较严重，如果采集频率过高，信号可能会跟踪失败，而且5 Hz组合后的结果相对于1 Hz和0.2 Hz提高并不多，因此在实际组合定位中可以选择1 Hz或者更低的频率。

图17 不同伪卫星频率组合后定位效果图Fig.17 Positioning result after combining different pseudosatellite frequencies

4 结 论

本文提出了改进的LM算法，并把改进的LM算法用于视觉VIO和伪卫星融合模型优化中。首先，分别测试了视觉VIO和伪卫星定位的精度。然后，把本文改进的LM算法与经典的LM算法进行对比。通过实例数据分析，场景1中利用本文改进的抗差LM算法融合后相对于伪卫星和视觉VIO定位精度分别提高了35.5%和59.0%；场景2中利用本文改进的抗差LM算法融合后相对于伪卫星和视觉VIO定位精度分别提高了27.8%和77.5%。

本文测试了伪卫星在短暂遮挡下组合系统定位性能，通过试验可以得出，即使伪卫星在遮挡情况下，组合系统定位性能基本不受影响，场景1和场景2的平均定位残差都在0.3 m以内，依然能保持定位的可靠性和连续性。最后，测试了不同频率(5、1和0.2 Hz)的伪卫星输出结果与视觉惯性里程计组合后的定位性能。通过分析可知，尽管频率越高，组合后定位精度越高，但是精度提高幅度较小，因此在实际组合定位中为了避免信号跟踪失败可以选择1 Hz或者更低的频率。