质量约束的三维模型建模方法

卜宁远　谢宇洋

摘  要：在当今的智能制造和工业软件设计领域，CAD和CAE是极为重要的技术。但现有的CAD和CAE模型表示方法不统一，在数据交换上需要耗费大量时间，造成了计算资源极大的浪费。非均匀有理B样条（NURBS）模型作为一种兼容CAD和CAE的模型表达方式，以样条曲线为基函数，无须进行交换即可进行等几何分析。本文提出了一种基于质量约束的NURBS体建模方法，将模型质量作为建模时的约束，使构建的模型符合等几何分析的要求。本文以带有复连通域的模型为例进行等几何分析，经过与主流商业软件的对比，最小值相同，最大值误差在10%以内，运行时间减少了4.61%，验证了此方法的正确性。

关键词：NURBS;建模方法;等几何分析

中图分类号：TP391.41     文献标识码：A

3D Modeling based on Mass Dependence

BU Ningyuan， XIE Yuyang

（School of Mechanical Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

BNY19971997@163.com; 826647688@qq.com

Abstract： CAD （Computer Aided Design） and CAE （Computer Aided Engineering） are extremely important technologies in today's intelligent manufacturing and industrial software design fields. However， representation methods of the existing CAD and CAE model vary， and it consumes a lot of time to exchange data， resulting in a great waste of computing resources. Non-uniform rational B-spline （NURBS） model， as a model expression compatible with CAD and CAE， takes spline curve as the basis function， and can perform isogeometric analysis without exchange. This paper proposes a NURBS modeling method based on mass dependence， which takes model mass as a constraint during modeling， so that the constructed model meets the requirements of isogeometric analysis. This paper takes a model with a complex connected domain as an example to perform isogeometric analysis. Compared with popular commercial software， the minimum value is the same， the maximum error is within 10%， and the running time decreases by 4.61%， which verifies the correctness of this method.

Keywords： NURBS; modeling method; isogeometric analysis

1   引言（Introduction）

隨着第四次工业革命的到来，多个国家都提出了工业数字化转型的战略规划，在智能制造领域，关键之一就是工业软件[1]。对于产品设计而言，专业的设计和仿真软件是必不可少的。为了降低设计成本，减少设计时间，将设计（CAD）与分析（CAE）集成一体化已是大势所趋。但迄今为止，CAD与CAE仍分为两个独立的领域[2]，因为采用的模型表达方式有所不同，导致两者之间产生了缝隙。当今主流CAD模型的表达多为边界表达B-Rep[3]和构造实体CSG[4]，而CAE模型为了适用于有限元分析（FEA）[5-6]，一般采用网格表示法。因此在整个设计与分析的过程中，模型会在CAD和CAE两种表示方式之间反复切换，拓扑结构被破坏，模型精度明显降低，时间成本大幅度提高[7-8]。

而NURBS参数化模型采用样条曲线作为基函数，能精确表示边界和曲面，且能提供模型内部的连续性参数化表达式，无须进行CAD和CAE之间的反复转化，产生的模型能直接用来进行等几何分析。等几何方法是有限元方法的继承与发展，该方法采用样条曲线作为基函数，具有较高的几何精确性。

但是，体参数化模型为了适用于等几何分析，必须要表示为零亏格的双变量张量曲面或三变量张量体，且相邻的体参数化单元之间的曲面要一致。因此需要对不满足等几何分析要求的体参数化模型进行分割处理，且等几何分析对模型的要求较高，分割后建立的模型还要在几何上满足等几何分析的要求。

2   相关研究（Related works）

对于CAD和CAE融合，可以进行CAD二次开发，在成熟的商业平台上进行融合;也可以使用重建法，在已知CAD模型边界的基础上得到内部控制点的信息，但需要进行大量的运算。体参数化建模不同于以上两种，具有计算简单、创建方便的优点。

在CAD模型剖分方面，相关学者已做了大量工作。大致方向可分为两种：（1）多边形凸分解，将多边形剖分为三角形、四边形及任意凸多边形集合;（2）网格分解，主要针对有限元模型，将CAD转换为CAE形式表达，如狄利克雷三角剖分法。由于等几何分析的特性，模型不需要再被转换成CAE表达，因此体参数化剖分主要采用第一种思路。

常见的多边形凸分解算法有两种：（1）几何单元区域剖分算法，如梯形分割算法[9];（2）考虑是否具有Steiner点的凸分解算法，如编码划分算法[10]和加权剖分算法[11]。但上述剖分算法仅在数学方面给出了多边形分割方案，没有考虑剖分结果是否符合分析标准，因此十分有必要评估四边形质量及其对等几何分析结果的影响。

本文提出了一种以NURBS体参数化模型质量为约束的建模方法，改进了适用于等几何分析的模型质量评估方法，将模型质量嵌入建模过程之中。首先递归分割模型截面，在分割过程中施加质量约束，使分割后的截面满足等几何分析的要求;然后使用扫描、拉伸、旋转、放样等操作进行体参数化映射，得到符合条件的体参数化模型。

3  体参数化建模与模型质量（Volume parametric modeling and model mass）

对于机械零件而言，大部分模型都可以定义截面及路径，通过扫描、拉伸、旋转、放样等操作完成模型构建。因此，为了使一般体参数化模型符合等几何分析的要求，要先对截面进行分割处理，将其分割成四边形的集合，以满足等几何分析中双变量张量曲面的要求。

3.1   截面剖分算法

本文使用的是递归剖分的方法，将整个模型控制点看作无向图，采用深度优先遍历，逐层向下寻找合适的剖分方案。该算法时间空间复杂度与传统算法相同，但在递归过程中加上了体参数建模所要求的约束，从数学问题转化为工程问题，因此最终结果更符合等几何分析的要求。

设算法输入为多边形子域集合POL，输出为四边形集合Quad，算法流程图如图1所示。

算法流程如下：

Step 1：若不为空，取作为，否则结束并返回。

Step 2：求解可行剖分线集合，设共有 种剖分连线方式，初始选择剖分线。

Step 3：，表示该子域不满足任何剖分条件;，表示已遍历所有的剖分连线方式。如结果不满足条件，则回溯至上一个剖分的子域，设为，。

Step 4：根据当前选择的剖分连线方式，创建一条新的NURBS曲线，同时获得两个新子域、，删除当前被剖分的子域。

Step 5：为凸四边形，存入集合;为五边形及以上，存入集合尾部;若均不符合，则回溯至上一个剖分的子域，。

Step 6：递归执行Step 1至Step 5。

3.2   剖分中的模型质量

在等几何分析中，计算域的参数化对应于有限元分析中的网格生成，对等几何分析结果的准确性是十分重要的[11]，需要将模型从物理域映射到参数域进行分析。使用雅可比矩阵将模型从物理域映射到参数域，雅可比矩阵如下：

根据已有质量理论，最标准的参数化模型应满足以下三个条件：（1）模型没有自交;（2）等参单元尽可能正交;（3）等参单元尽可能均匀。这样会使雅可比的值接近或等于1，参数域映射的效果最佳。而扭曲、自交、不均匀的曲面均会使雅可比的质量变差从而破坏参数域映射，也会使等几何分析求解偏微分方程的过程变得十分困难，因此在剖分中我们要尽量避免出现这种曲面。对于不合格的曲面，需要制定一系列检测方法。

对于六面体网格，主流方法已经给出了一系列检测指标：对角线度量、缩放雅可比、扭曲度和宽高比等。对于NURBS曲面而言，可以在曲面上取若干等参单元看作四边形进行质量评估。我们在此选择了区域面积A、宽高比asp和扭曲度dist三个指标作为衡量四边形的依据，以下是这三个指标的详细定义。

3.2.1   区域面积

如图2所示，我们把每一个等参单元看作一个小的四边形，为了衡量它是否均匀，是否接近最好的分析模型，我们首先定义边向量，然后将其分为四个区域，定义坐标轴。

其中，为四边形的角点坐标。为了衡量四个角点区域是否在统一平面上，定义每一个角点处的法向量：

为了方便计算，设它们的单位向量：

定义一个中心法向量作为全局的法向量和单位向量，分别为：

将整个区域按照坐标的上下左右軸分成四块，如图3（a）所示，则可以根据已知的参数求得每块的区域面积：

根据几何知识可以知道，若（即该四边形某一区域的面积）小于0，则该片一定是退化的，如图3（b）所示，即为凹四边形。

对于NURBS曲面而言，由于边界是曲线，因此直接按照角点求法向量是没有意义的，但每个面的控制点和等参线可以构成若干个小的等参单元。等参单元最好的情况是四条边两两正交，而退化的等参单元一定不满足边边正交，因此会拉低整体的图形质量。因此，所有等参单元面积大于0的数量越多越好。当凹四边形出现时，必然会有一个区域面积等于或小于零。凹多边形的出现使得等几何分析中的参数域映射和求解偏微分方程的效果很差，是一定不能出现在分析模型之中的，因此利用区域面积法可以很简单地判别出不符合情况的条件之一，且与普通四边形剖分中的射线法相比更具有鲁棒性。

3.2.2   宽高比

NURBS等参单元的结构越均匀越好，因此可以定义高宽比来评价等参单元是否均匀：

其中，A为四边形面积，宽高比值域为，经验表明为可接受域。宽高比排除的是看起来很“窄”的四边形，这类四边形的出现会使控制点的分布极其不均匀，导致等几何参数域的映射效果很差，也是一种不能出现在体参数化模型上的情况之一。宽高比的求解只需要在区域面积的基础上再加上一步运算即可，消耗的资源很少，产生的效果却很好。

3.2.3   扭曲度

为了衡量四边形是否扭曲，首先要建立一个参照系，设一个位于坐标原点的正方形的面积;再根据式（3）可以算出所有高斯积分点的最小雅可比值，则扭曲度定义为：

扭曲是衡量从参数空间到世界坐标映射行为的良好程度的一种度量，值域为，越接近1效果越好，因此将可接受域设为。

根据以上三个指标，可以较为准确地检查剖分截面的均匀性、正交性和扭曲度，且计算也十分简单，不会占用太多时间和空间。这几个指标可以在递归时的判别条件中加入，在连接分割线后，依次检查这三个值，若有不在接收域的情况则不合格，否则放入备选库，作为可能的选项之一。

3.3   体参数化映射

得到了剖分好的NURBS四边形曲面后，可以使用扫描、拉伸、旋转、放样等操作进行体参数化映射。拉伸体模型可以通过截面控制点沿直线方向的仿射变换得到，在CAD中多用于凸台等结构的创建。如果模型的路径不是直线而是圆弧，则可以进行旋转体映射。若拉伸的路径不是直线也不是规则圆弧，则可以用扫掠体造型。

对于无法用一个截面生成的模型，可以考虑采用放样体造型，沿曲线路径插值放样体的造型方法和扫掠体相似，需要先统一各个截面的阶数、节点矢量及控制点数量，确保截面与该点曲线切矢垂直，再通过反求控制点即可得到沿曲线路径的放样体。而不沿路径插值的放样方式则无须保证各截面与曲线切矢垂直。

对于机械零件而言，大部分模型都可以通过这几种建模方法得到。在得到了体参数化模型之后便可以直接进行等几何分析，而不需要再花大量时间进行网格划分。

4   实例（Examples）

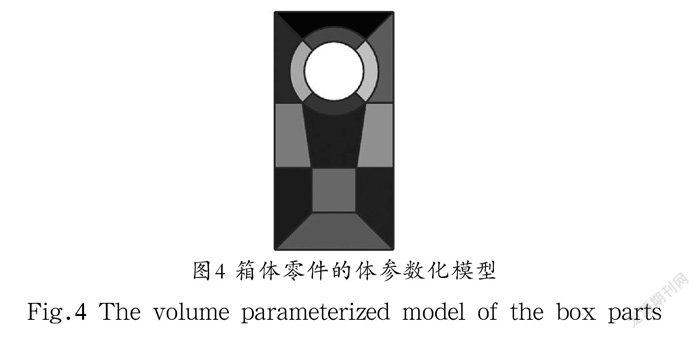
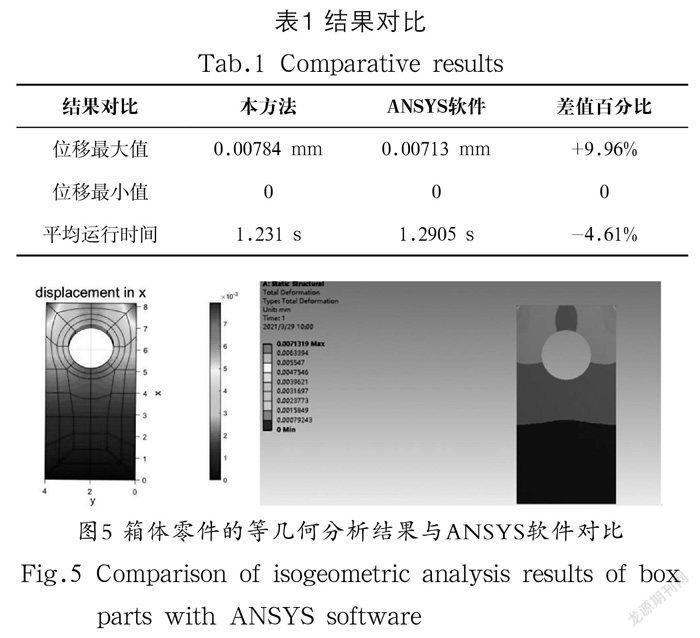
本部分以一个带有通孔的箱体配件为例，该配件经常用于减速箱上，顶部受力，底部有固定约束，是典型的机械部件之一。我们在其上表面施加力约束，下表面固定，进行静力学分析。由于配件带有通孔，因此进行剖分之前需要在圆上插入若干的点，再进行剖分，且圆孔周围的分割线也要保持一定的弧度以免与圆相交，再进行拉伸操作，最后得到的体参数化模型如图4所示。再使用MATLAB软件对模型进行等几何分析，得出的结果与ANSYS软件对比如表1和图5所示，位移的最小值相同，最大值相差在10%以内，同时平均运行时间减少了4.61%，证明了本文方法的有效性。

5   结论（Conclusion）

本文为CAD和CAE的无缝集成提供了一种新的思路，即以NURBS样条曲线模型代替原有的CSG和B-Rep模型，这样使得进行分析的时候无须数据格式和表达方式的转换，大大降低了时间复杂度和内存空间的消耗。本文以箱体配件为例，展示了如何对带有复连通域的图形进行剖分和建模，经过与商业软件的对比得到了较好的结果。

但此方法仍然存在一些问题。等几何分析对模型的要求较高，一些不规则图形如点阵材料等还无法通过简单的扫描、拉伸、旋转、放样等简单的体参数化映射方法得到。同样的，对于一些细微的特征如倒角、圆角和小孔等也无法完全保留，这也是我们下一步主要研究的方向。另外，为了提高体参数化建模保留原有几何特征的能力，使构建的模型更加精确，对体参数化模型布尔运算也需要进一步研究。

参考文献（References）

[1] 宁振波.力筑工业之基重铸智造灵魂[J].软件导刊，2021，  20（01）：7-11，6.

[2] SMIT M S， BRONSVOORT W F. Integration of design and analysis models[J]. Computer-Aided Design and Applications， 2009， 6（6）：795-808.

[3] KIM B C， MUN D. Feature-based simplification of boundary representation models using sequential iterative volume   decomposition[J]. Computers & Graphics， 2014， 38：97-107.

[4] 罗月童，樊晓菁，俞盛朋，等.基于面壳封闭的B-Rep至CSG转换算法[J].计算机辅助设计与图形学学报，2014，26（10）：1673-1680.

[5] AVERSA R， PETRESCU F I T， PETRESCU R V V， et al. Biofidel FEA modeling of customized hybrid biological hip joint design part Ⅱ： Flexible stem trabecular prostheses[J]. American Journal of Biochemistry and Biotechnology， 2016， 12（4）：23-29.

[6] KASIK D J， BUXTON W， FERGUSON D R. Ten CAD challenges[J]. IEEE Computer Graphics and Applications， 2005， 25（2）：81-92.

[7] PARK H S， DANG X P. Structural optimization based on CAD-CAE integration and metamodeling techniques[J].Computer-Aided Design， 2010， 42（10）：889-902.

[8] PAN Z， WANG X， TENG R， et al. Computer-aided design-while-engineering technology in top-down modeling of mechanical product[J]. Computers in Industry， 2016， 75： 151-161.

[9] 王金敏，劉季烨，方沂.基于梯形分解的不规则多边形干涉算法[J].工程图学学报，2005（06）：52-57.

[10] 肖忠晖，卢振荣，张谦.简单多边形凸单元剖分的编码算法[J].计算机学报，1996（06）：477-481.

[11] 王博，李笑牛，李华.一种加权剖分简单多边形为三角形和凸四边形子域的算法[J].中国图象图形学报，2002，7（005）：   486-490.

作者简介：

卜宁远（1997-），男，硕士生.研究领域：CAD/CAE.

谢宇洋（1997-），男，硕士生.研究领域：CAD/CAE.