先存断层产状及其组合关系对反转构造变形影响的离散元数值模拟研究
孙倩倩, 刘志娜*, 余一欣, 唐贤君, 陈 石, 彭 浩
先存断层产状及其组合关系对反转构造变形影响的离散元数值模拟研究
孙倩倩1, 2, 刘志娜1, 2*, 余一欣1, 2, 唐贤君3, 陈 石1, 2, 彭 浩1, 2
(1. 中国石油大学(北京) 油气资源与探测国家重点实验室, 北京 102249; 2. 中国石油大学(北京) 地球科学学院, 北京 102249; 3. 中海石油(中国)有限公司上海分公司, 上海 200335)
反转构造在我国含油气盆地中广泛发育, 对于油气勘探具有重要意义。本文采用离散元颗粒流方法研究了先存正断层的陡缓程度、倾向组合关系和距离挤压端的远近等因素对断层的反转构造发育及其反转量的影响。模拟结果显示, 先存断层的产状及其距离挤压端的远近会影响先存断层的反转次序、反转量, 进而影响盖层内反转构造的发育。当先存正断层倾向指向挤压端时, 若缓倾正断层靠近挤压端, 则缓倾断层发生反转, 而远离挤压端的陡倾断层未发生反转; 若陡倾断层靠近挤压端, 则缓倾断层和陡倾断层同时发生反转。当先存正断层倾向背离挤压端时, 无论靠近还是远离挤压端, 缓倾断层和陡倾断层均发生反转。当先存正断层倾向相对(地堑)时, 若缓倾正断层更靠近挤压端, 则缓倾断层发生明显反转, 而陡倾断层未发生反转; 若陡倾正断层靠近挤压端, 缓倾断层和陡倾断层同时发生反转。在先存断层均发生反转的模型中, 无论先存断层倾角大小, 靠近挤压端的先存断层的反转量最终均大于远离挤压端的先存断层的反转量。最终, 离散元模拟结果还与西湖凹陷垂直于反转构造带走向的地震剖面进行对比, 有很好的吻合性。
离散元模拟; 反转构造; 先存断层产状; 反转次序; 西湖凹陷
0 引 言
反转构造在我国含油气盆地中广泛发育, 具有良好的聚烃能力和优越的圈闭条件, 因此成为油气勘探的首选(徐子英等, 2012)。运用物理模拟和数值模拟的方法对反转构造发育的影响因素进行研究, 对于提高反转构造发育特征的认识, 辅助盆地构造演化特征分析, 提高勘探成功率具有重要意义。
为了更清楚地了解反转构造发育的运动学和几何学影响因素, 国内外学者运用物理模拟和数值模拟方法进行了大量的模拟实验, 研究了边界条件(Buchanan and Mcclay, 1991; 闫淑玉等, 2016)、基底先存断层(Buchanan and Mcclay, 1992; Marques and Nogueira, 2008; Adel, 2014; Smith et al., 2017)、构造应力(Ventisette et al., 2006; 马宝军等, 2006)、岩性层的强弱(Brun and Nalpas, 1996)、沉积和剥蚀作用(Panien et al., 2005; 吴珍云等, 2018)和岩浆作用(Martíne et al., 2018)等地质因素对反转构造发育的影响。其中先存断层产状是重要的主控因素之一, 前人对此进行了大量研究, Brun and Nalpas (1996)通过物理模拟发现, 挤压方向与地堑夹角小于45°时先存断层才能反转; Marques and Nogueira (2008)采用物理模拟研究发现, 当多条先存断层存在时, 断层反转程度与其距离挤压端的远近有关; 闫淑玉等(2016)采用物理模拟研究发现, 挤压边界与先存正断层之间距离对反转构造样式具有明显影响; Adel (2014)认为, 早期伸展断层系统的几何形态明显影响了倒转断层的滑移量和倒转背斜的几何形态; Ventisette et al. (2006)通过物理模拟认为, 边界断层与倾斜角的大小对后期挤压构造的形态演化具有明显控制作用; 陈均亮等(2009)通过砂箱模拟实验认为, 断面较缓的率先变形, 其对应的背斜带翼部陡且褶皱幅度大。前人对于先存断层产状对反转构造影响的研究多对单条断层进行, 然而对于多条不同产状组合的先存断层所产生的反转构造变形还没有系统地研究。
离散元模拟是研究构造动力学的有效方法。自1971年以来的研究实践表明, 其适用于非连续介质的破裂问题研究(Cundall, 1971; Cundall and Strack, 1979), 已广泛用于研究构造地质中的大变形问题, 如岩块的节理破裂(Zhao et al., 2007; Ren et al., 2012)、断层及断层相关褶皱(Strayer and Suppe, 2002; 周易等, 2019; 辛文等, 2020)、变换构造发育机制(Imbera et al., 2004)、盐构造(Yin et al., 2009; 徐雯峤等, 2020)等诸多地质构造演化过程。
本文以离散元原理为基础, 使用颗粒流数值模拟方法(PFC2D)构建二维离散元模型, 模拟反转构造变形过程, 明确早期正断层的陡缓程度、倾向组合关系和距离挤压端的远近等因素对正断层反转过程中断背斜形成的影响。模拟结果对寻找与反转构造相关的断背斜圈闭具有一定指导作用。
1 模型设置
在盆地伸展过程中, 往往产生一系列同倾与对倾断层, 为探究其倾角、倾向和距离挤压端的远近对后期反转构造的影响, 本文采用颗粒流离散元模拟方法建立了6个模型。每个模型包含两条先存断层, 远离挤压端的断层命名为F1, 靠近挤压端的断层命名为F2。通过改变两个先存断层F1和F2的倾角(60°和45°)和倾向(朝向或背离挤压端), 共设计3组模型(表1和图1)。在模型1和模型2中, 两断层同倾, 倾向朝向挤压端; 在模型3和模型4中, 两断层同倾, 倾向背离挤压端; 在模型5和模型6中, 两断层对倾。模型1、模型3和模型5中, F1为陡倾断层, F2为缓倾断层; 模型2、模型4和模型6中F1为缓倾断层, F2为陡倾断层(表1和图1)。
模型以圆形刚性颗粒集合体模拟主体地层, 两侧以及底部以墙体作为边界, 通过右侧墙体以0.05 m/s固定速度向左运动模拟挤压过程。6个模型均设定长120 m, 高20 m。岩层之间设有薄层的软弱层来模拟地层层理面, 岩层厚度为3 m, 软弱层厚度为1 m。模型1~6从底部到顶部分布着5层岩层(3 m)及其中的薄弱层(1 m), 其中最底层为塑性层。先存断层F1和F2设置在塑性层的上方。所有模型内, 坐标原点为模型的左下角, 右方为方向正方向, 上方为方向正方向。先存断层F1底部位于=40 m、=4 m处, 先存断层F2位于=80 m、=4 m处, 并将不同断块设定以不同颜色。
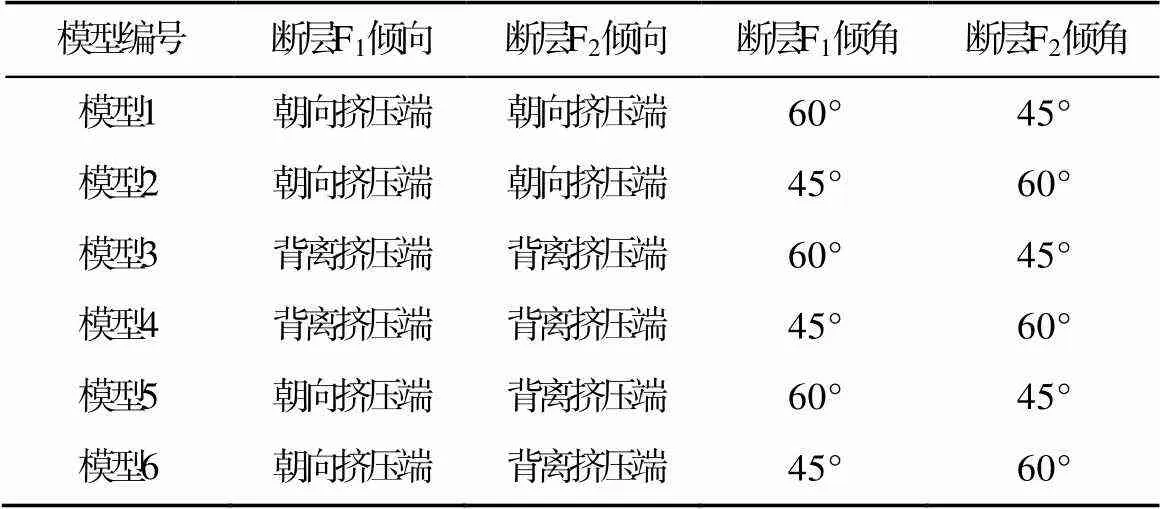
表1 离散元数值模型参数表

图1 反转构造离散元模型示意图
颗粒流模拟方法所赋予模型内颗粒的微观力学参数与宏观岩石力学参数是不同的, 两者之间有一定的转换关系。通过赋予颗粒微观力学参数来模拟双轴压缩实验, 以便获取宏观力学参数。所得的宏观力学参数与实际岩体的宏观岩石力学参数进行对比, 通过一定的规律反复尝试, 当模拟实验结果与实际岩体岩石力学参数相吻合时, 所赋予颗粒的微观力学参数即可用在模型中。前人研究已经详细阐述了微观力学参数的获取方法, 在此不再赘述(Chenget al., 2009; Liu and Koyi, 2013)。本文采用相同的方法, 现将模型地层的岩石力学参数设置如下: 所有岩层密度均为2630 kg/m3, 所有层颗粒均服从高斯分布。对于3 m厚的脆性岩层, 颗粒粒径分布范围为0.144~0.230 m, 微观颗粒间摩擦系数为1(相当于岩层摩擦系数0.57, 即内摩擦角30°), 粘结强度为3×106N, 切向刚度(s)为1×109N/m, 法向刚度(n)为4×109N/m(相当于岩层粘结强度为10 MPa, 杨氏弹性模量为30 GPa, 泊松比为0.25, 符合砂岩力学性质)。对于1 m厚的软弱层, 颗粒粒径分布范围为0.083~0.133 m, 摩擦系数与粘结强度均为0, 切向刚度为1×109N/m, 法向刚度为4×109N/m; 法向刚度与切向刚度比值(泊松比)为0.25。模型底部塑性层粒径分布于0.144~0.230 m之间, 摩擦系数为1, 切向和法向粘结强度均为3×106N/m, 切向刚度为5×106N/m, 法向刚度为1.5×107N/m(相当于岩石杨氏模量为30 GPa, 泊松比为0.33, 符合泥岩的力学性质)。在先存断层位置设置厚度为1 m的断层面, 切向刚度为1×109N/m, 法向刚度为4×109N/m, 颗粒间粘结强度和摩擦系数均为0(表2)。模型内所有墙体摩擦系数为1, 切向刚度为1×109N/m, 法向刚度为3×109N/m。
为了研究先存断层倾角、倾向和位置的变化对其在之后挤压过程中产生的反转量的影响, 我们选取初始模型中先存断层F1上盘分布的点1、点2和点3, 先存断层F2上盘分布的点4、点5和点6, 依据坐标位置确定6个颗粒并追踪监测其在反转过程中的位移变化规律(图1)。在挤压过程中, 岩层随着右侧墙体的挤压而移动, 颗粒在方向的位移不能表示断层上盘在方向的反转位移量, 因此, 我们用断层上盘不同深度的各监测点方向的位移变化趋势, 来分析先存断层的反转量的变化趋势。
2 模拟结果
2.1 两断层同倾且倾向指向挤压端
2.1.1 模型反转构造变形过程
模型1中, 在挤压初期(压缩率为1.67%时), 模型的变形集中在靠近挤压端的缓断层F2处, 先存正断层F2发生反转, 形成不对称背斜(图2a)。随着挤压作用的持续进行, 在压缩率为3.33%~6.67%时, F2反转量进一步增大, 同时, 靠近挤压端地层开始发生变形(图2b~d)。当压缩率为8.33%时, F2反转量持续增加, 切穿上部岩层, 形成隆起幅度较大的背斜, 靠近挤压端的岩层内发育多条逆冲断层(图2e)。在挤压过程中, 远离挤压端的陡断层F1未发生明显反转(图2)。模型1结果揭示, 当模型内含有两条同倾断层(倾向指向挤压端)且倾角较小的断层靠近挤压端时, 构造变形主要集中在靠近挤压端的缓断层F2上盘, 同时, 在靠近挤压端的岩层内也有逆冲断层F3~F4产生(图2)。
模型2中, 在挤压初期(压缩率为1.67%时), 远离挤压端的缓断层F1和靠近挤压端的陡断层F2均发生小幅度反转(图3a)。随着挤压量的增加, 当压缩率为3.33%~6.67%时, 两先存断层的反转量继续增加, 其中F2反转量相对较大, 另外, 靠近挤压端地层发生变形, 产生逆冲断层F3~F5(图3b~d)。当压缩率为8.33%时, 两断层上盘均形成非常明显的背斜构造, 其中F1上盘背斜构造较陡, F2上盘背斜构造更为宽缓(图3e)。模型2结果揭示, 当模型内含有两条同倾断层(倾向指向挤压端)且倾角较小的断层远离挤压端时, 两断层同时发生反转, 且随着压缩率的增大, 靠近挤压端一侧陡倾断层F2的反转幅度相对更大, 在靠近挤压端的岩层内也有逆冲断层F3~F5产生(图3)。

表2 离散元模型微观力学参数表
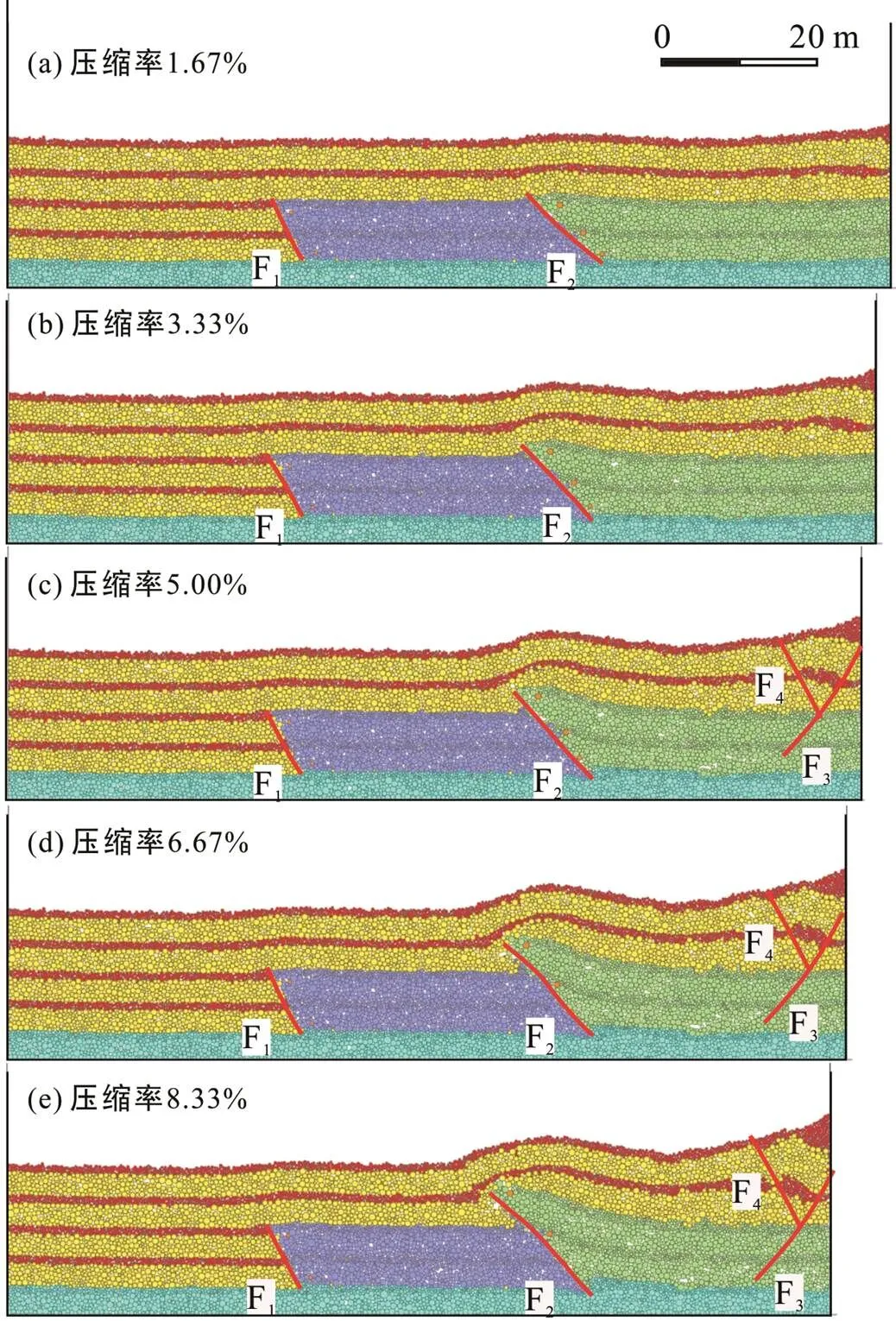
图2 离散元数值模型1变形过程解释图
2.1.2 先存断层F1和F2的位移变化
在模型1和模型2中, 我们监测了先存断层F1和F2上盘在挤压过程中方向上位移的变化趋势。
在模型1中, 远离挤压端的陡倾断层F1反转量远远小于靠近挤压端的缓倾断层F2的反转量(图4)。F1和F2的反转量随着深度的增加而减少(图4)。在压缩率为8.33%时, F1上盘的点1、点2和点3在方向位移分别为0.05 m、0.4 m和0.4 m; F2上盘分布的点4、点5和点6在方向位移分别为2.2 m、4 m和5.7 m(图4)。因此, 在模型1中, 靠近挤压端的缓倾断层F2发生明显反转, 而远离挤压端的陡倾断层F1未发生明显反转。

图3 离散元数值模型2变形过程解释图

图4 模型1中同倾断层F1(60°)和F2(45°)在Y方向上位移随压缩率变化图
在模型2中, 远离挤压端的缓倾断层F1和靠近挤压端的陡倾断层F2在方向上的位移量随着压缩率的增加同时增大, 且F1和F2同时发生明显反转(图5)。F1的反转量小于F2的反转量。F1和F2的反转量(方向位移)随着深度的增加而减少(图5)。在压缩率为8.33%时, F1上盘分布的点1、点2和点3在方向位移分别为0.8 m、1 m和1.6 m; F2上盘分布的点4、点5和点6在方向位移分别为1.2 m、1.4 m和4.4 m(图5)。因此, 在模型2中, 远离挤压端的缓倾断层F1和靠近挤压端的陡倾断层F2同时发生明显反转, 且断层F2反转量大于断层F1反转量。
综上, 当模型中含有两条同倾断层且倾向指向挤压端时, 在缓倾断层靠近挤压端的模型(模型1)中, 缓倾断层发生明显反转, 而陡倾断层未发生明显反转; 在缓倾断层远离挤压端的模型(模型2)中, 缓倾断层和陡倾断层同时发生明显反转, 靠近挤压端的陡倾断层的反转量大于远离挤压端的缓倾断层的反转量。此外, 陡倾断层在其靠近挤压端的模型中的反转量(1.2 m、1.4 m和4.4 m)大于其在远离挤压端的模型中的反转量(0.05 m、0.4 m和0.4 m); 缓倾断层在其靠近挤压端的模型中的反转量(2.2 m、4 m和5.7 m)大于其在远离挤压端的模型中的反转量(0.8 m、1 m和1.6 m)。
2.2 两断层同倾且倾向背离挤压端
2.2.1 模型反转构造变形过程
模型3中, 在挤压初期(压缩率为1.67%), 远离挤压端的陡倾断层F1和靠近挤压端的缓倾断层F2同时发生反转, 但F2的反转量比F1的反转量大(图6a)。随着挤压作用的持续进行, 在压缩率为3.33%~6.67%时, F1的反转量增加缓慢, 而F2反转量增加明显, 同时, 靠近挤压端的岩层内发育多条逆冲断层F3~F4(图6b~d)。当压缩率为8.33%时, F1反转量较前一阶段无明显增加, 而F2反转量一直持续增加, 切穿上部岩层, 形成隆起幅度较大的背斜(图6e)。模型3结果揭示, 当模型内含有两条同倾断层(倾向背离挤压端)且倾角较小的断层靠近挤压端时, 两个先存断层同时发生反转, 但靠近挤压端的缓断层F2的反转量较大, 同时, 在靠近挤压端的岩层内有逆冲断层F3~F4产生(图6)。

图5 模型2中同倾断层F1(45°)和F2(60°)Y方向位移随压缩率变化图
模型4中, 在挤压初期(压缩率为1.67%), 远离挤压端的缓倾断层F1最早开始发生反转, 而靠近挤压端的陡倾断层F2未发生反转(图7a)。随着挤压作用的持续进行, 在压缩率为3.33%时, F1的反转量持续增加, 而F2开始发生反转, 同时, 靠近挤压端的岩层内发育反冲断层F3~F4(图7b)。当压缩率为5.00%~6.67%时, F1和F2的反转量均继续增大(图6c、d)。当压缩率为8.33%时, 两个先存断层发生明显反转, 切穿上部岩层, 形成隆起幅度较大的背斜(图7e)。模型4结果揭示, 当模型内含有两条同倾断层(倾向背离挤压端)且倾角较大的断层靠近挤压端时, 远离挤压端的缓倾断层F1先发生反转, 靠近挤压端的陡倾断层F2随后发生反转。随着挤压作用的进行, 在靠近挤压端的岩层内有反冲断层F3~F4产生(图7)。

图6 离散元数值模型3变形过程解释图
2.2.2 先存断层F1和F2的位移变化
在两断层同倾且倾向背离挤压端的模型3和模型4中, 我们监测了先存断层F1和F2上盘在挤压过程中方向上的位移变化趋势。
在模型3中, 远离挤压端的陡倾断层F1和靠近挤压端的缓倾断层F2的方向上的位移量均随着压缩率的增加而增大, 即先存断层F1和F2同时发生明显反转(图8)。F1的反转量小于F2的反转量。F1和F2的反转量(方向位移)随着深度的增加而减少(图8)。在压缩率为8.33%时, F1上盘的点1、点2和点3的方向位移分别为1.2 m、1.3 m和1.6 m; F2上盘的点4、点5和点6的方向位移分别为1.9 m、4.2 m和4.1 m(图8)。因此, 在模型3中, 远离挤压端的陡倾断层F1和靠近挤压端的缓倾断层F2均发生反转, 且断层F2反转量远大于断层F1反转量, 两者反转量均随着深度的增加而减少。
在模型4中, 远离挤压端的缓倾断层F1位移量小于靠近挤压端的陡倾断层F2的位移量(图9)。先存断层F1和F2的反转量(方向位移)随着深度的增加而减少(图9)。在压缩率小于6.67%时, F1的反转量大于F2的反转量; 在压缩率大于6.67%时, F2上部的反转量快速增大, 反超了F1的反转量(图9)。在压缩率为8.33%时, F1上盘的点1、点2和点3的方向位移分别为2.1 m、2.3 m和2.6 m; F2上盘的点4、点5和点6的方向位移分别为0.9 m、2.7 m和3.6 m (图9)。因此, 在模型4中, 远离挤压端的缓倾断层F1和靠近挤压端的陡倾断层F2同时反转, 且反转量均随着深度的增加而减少。在挤压初期, 缓倾断层F1的反转量大于陡倾断层F2的反转量; 在挤压后期, 陡倾断层F2上部地层的反转量反超缓倾断层F1的反转量。

图7 离散元数值模型4变形过程解释图
综上, 当模型中含有两条同倾断层且倾向背离挤压端时, 缓倾断层和陡倾断层均发生反转。在缓倾断层靠近挤压端的模型(模型3)中, 靠近挤压端的缓倾断层的反转量远大于远离挤压端的陡倾断层的反转量。在缓倾断层远离挤压端的模型(模型4)中, 挤压初期, 缓倾断层反转量较大; 挤压后期, 陡倾断层反转量快速增加, 且其中上部地层反转量反超了远离挤压端的缓倾断层的反转量。陡倾断层在其靠近挤压端的模型(模型4)中的反转量(0.9 m、2.7 m和3.6 m)大于其在远离挤压端的模型(模型3)中的反转量(1.2 m、1.3 m和1.6 m); 缓倾断层在其靠近挤压端的模型(模型3)中的反转量(1.9 m、4.2 m和4.1 m)大于其在远离挤压端的模型(模型4)中的反转量(2.1 m、2.3 m和2.6 m)。
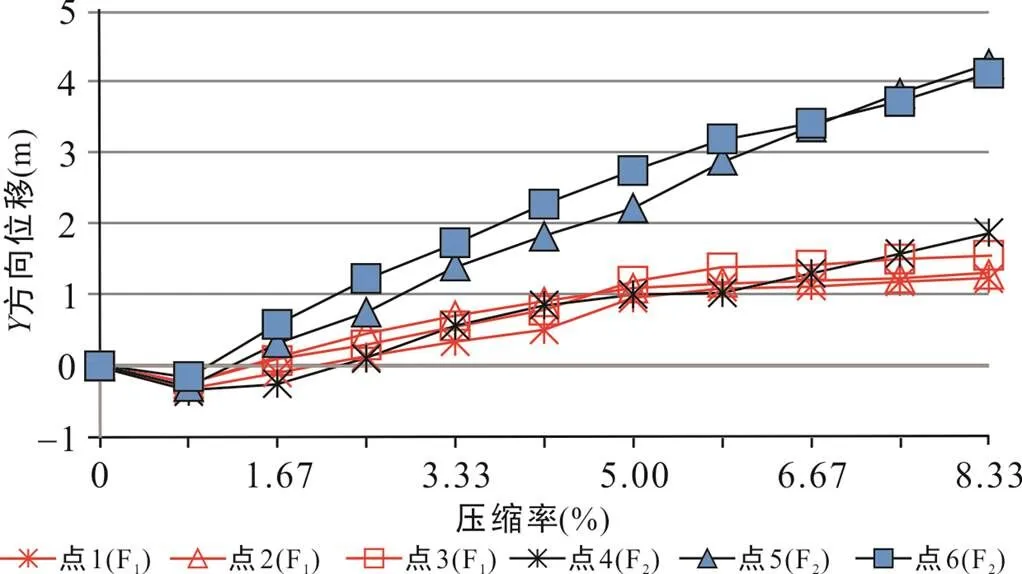
图8 模型3中同倾断层F1(60°)和F2(45°)Y方向上位移随压缩率变化图

图9 模型4中同倾断层F1(45°)和F2(60°)Y方向位移随压缩率变化图
2.3 两断层对倾
2.3.1 模型反转构造变形过程
在模型5中, 在挤压初期(压缩率为1.67%), 靠近挤压端的缓断层F2最早开始发生反转, 而远离挤压端的陡倾断层F1未发生反转(图10a)。随着挤压作用的持续进行, 在压缩率为3.33%时, F2继续反转, 挤压端一侧的地层产生变形, 发育断层F3(图10b)。当压缩率增大为5.00%~6.67%时, 挤压端一侧地层继续变形, F2下盘发育前冲断层F4, 上盘发育前冲断层F6, 而F1未发生明显反转(图10c、d)。当压缩率为8.33%时, F2反转量持续增加, 反冲断层F4上盘变形强度持续增大(图7e)。模型5结果揭示, 当模型内含有两条对倾断层(地堑)且倾角较小的断层靠近挤压端时, 靠近挤压端的缓倾断层F2先发生反转, 并在其上盘发育前冲断层F6, 远离挤压端的陡倾断层F1未发生明显反转, 同时, 在靠近挤压端的岩层内也有逆冲断层F3~F5产生(图10)。
在模型6中, 在挤压初期(压缩率为1.67%), 远离挤压端的缓倾断层F1(倾向朝向挤压端)最早开始发生反转, 而靠近挤压端的陡倾断层F2(倾向背离挤压端)未发生反转(图11a)。随着挤压作用的持续进行, 在压缩率为3.33%时, F2开始反转, 挤压端一侧的地层产生变形发育断层F3(图11b)。当压缩率增大为5.00%~6.67%时, F2的反转作用增强, 其上盘发育前冲断层F4, 而F1反转作用减弱(图11c、d)。当压缩率为8.33%时, F2反转量持续增加(图11e)。模型6结果揭示, 当模型内含有两条对倾断层(地堑)且倾角较大的断层靠近挤压端时, 挤压初期, 远离挤压端的缓倾断层F1先发生反转, 靠近挤压端的陡倾断层F2晚于断层F1发生反转, 且反转作用持续增加, 最终发育不对称断背斜构造, 同时, 在靠近挤压端的岩层内也有逆冲断层F3和F5产生(图11)。
2.3.2 先存断层F1和F2的位移变化
在两断层同倾且倾向背离挤压端的模型5和模型6中, 我们监测了先存断层F1和F2上盘在挤压过程中方向的位移变化趋势。
在模型5中, 远离挤压端的陡倾断层F1(倾向指向挤压端)反转量小于靠近挤压端的缓倾断层F2(倾向背离挤压端)的反转量(图12)。F1的反转量(方向位移)几乎为0, 监测其上盘的点1、点2和点3的方向位移分别为0 m、0.3 m和0 m(图12)。F2的反转量(方向位移)随着深度的增加而减少, 监测其上盘的点4、点5和点6的方向位移分别为2 m、2.6 m和4.2 m(图12)。因此, 在模型5中, 远离挤压端的陡倾断层F1并未产生明显反转, 而靠近挤压端的缓倾断层F2发生反转, 且反转量随着深度的增加而减少。
在模型6中, 远离挤压端的缓倾断层F1和靠近挤压端的陡倾断层F2的位移量随着压缩率的增加同时增大, 即先存断层F1和F2同时发生反转(图13)。F1的位移量小于F2的位移量。先存断层F1和F2的反转量(方向位移)随着深度的增加而减少(图13)。在压缩率为8.33%时, F1上盘的点1、点2和点3的方向位移分别为0.9 m、1.3 m和1.7 m; F2上盘的点4、点5和点6的方向位移分别为1.8 m、3.3 m和4.4 m(图13)。因此, 在模型6中, 远离挤压端的缓倾断层F1和靠近挤压端的陡倾断层F2同时发生明显反转, 且断层F2反转量明显大于断层F1反转量, 二者反转量随着深度的增加而减少。
综上, 当模型中含有两条对倾断层(地堑)时, 在缓倾断层靠近挤压端的模型(模型5)中, 缓倾断层发生明显反转(反转量自下而上约为2 m、2.6 m和4.2 m), 而陡倾断层基本未发生反转; 在缓倾断层远离挤压端的模型(模型6)中, 缓倾断层和陡倾断层同时发生反转, 靠近挤压端的陡倾断层的反转量(1.8 m、3.3 m和4.4 m)远大于远离挤压端的缓倾断层的反转量(0.9 m、1.3 m和1.7 m)。同时, 缓倾断层靠近挤压端的模型中, 先存断层的反转量比缓倾断层远离挤压端的模型要大。
3 讨 论
3.1 先存断层产状对反转构造变形的影响
模拟结果揭示, 在基底滑脱层存在的情况下, 先存断层的反转量随着深度的增加而降低, 并在浅层沉积层内形成了不同幅度的背斜。无论断层产状如何, 在挤压后期, 靠近挤压端断层的反转量远大于远离挤压端断层的反转量, 因而, 先存断层距离挤压端的远近位置对其反转量的影响更明显。Marquesand Nogueira (2008)的物理模拟结果也显示, 当模型中含有多条先存断层时, 断层反转程度与其距离挤压端的距离有关。闫淑玉等(2016)也提出挤压边界与先存正断层之间距离对反转构造样式具有明显影响。另外, 基底先存正断层的产状对断层的反转次序以及其上盘断背斜的发育有更明显的影响。
当模型中含有两条同倾断层且倾向指向挤压端时, 在缓倾断层靠近挤压端的模型1中, 缓倾断层由于其倾角小且距离挤压端更近, 因而更容易发生反转, 吸收了绝大部分挤压量, 其上盘形成隆起幅度较大的背斜; 而倾角大且距离挤压端距离较远的陡倾断层几乎未发生反转。在缓倾断层远离挤压端的模型2中, 缓倾断层和陡倾断层同时发生反转, 挤压初期的两断层反转量无太大差异; 挤压中后期由于受到靠近挤压端地层变形的影响, 靠近挤压端的陡倾断层上部地层的反转量迅速增大, 最终其反转量远大于远离挤压端的缓倾断层的反转量。因此, 在靠近挤压端的陡倾断层上盘形成宽度较小两翼较陡的背斜, 远离挤压端的缓倾断层上盘形成宽度较大两翼较缓的背斜。
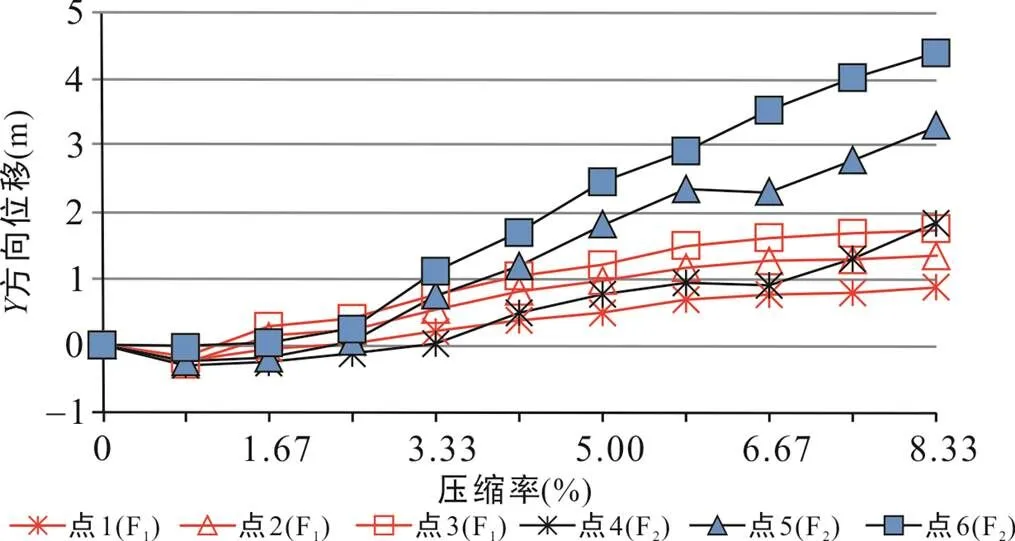
图13 模型6中同倾断层F1(45°)和F2(60°)Y方向位移随压缩率变化图
当模型中含有两条同倾断层且倾向背离挤压端时, 缓倾断层和陡倾断层均发生反转。在缓倾断层靠近挤压端的模型3中, 靠近挤压端的缓倾断层由于其倾角小且距离挤压端更近, 更容易发生快速反转; 最终缓倾断层的反转量远大于远离挤压端的陡倾断层的反转量, 缓倾断层上盘形成了隆起幅度更大的背斜。在缓倾断层远离挤压端的模型4中, 挤压初期, 缓倾断层由于倾角小, 更容易发生反转, 其反转量较大; 挤压后期, 受靠近挤压端地层变形的影响, 陡倾断层反转量快速增加, 且其中上部地层反转量反超了远离挤压端的缓倾断层的反转量。
当模型中含有两条对倾断层且倾向相对(地堑)时, 在缓倾断层靠近挤压端而倾向背离挤压端的模型5中, 缓倾断层发生明显反转, 其上盘发育了前冲断层和背斜构造, 而陡倾断层基本未发生反转。在缓倾断层远离挤压端而倾向指向挤压端的模型6中, 缓倾断层和陡倾断层同时发生反转; 挤压初期, 缓倾断层由于倾角小更容易发生反转, 其反转量稍大, 其上盘隆起幅度稍大; 挤压中后期, 缓断层的反转速率逐渐减小, 反转量增加极其缓慢, 陡倾断层由于其距离挤压端距离近, 继续反转, 反转量反超远离挤压端的缓倾断层, 并在其上盘生成新的逆冲断层。
模型结果还揭示, 当缓倾断层靠近挤压端且倾向指向挤压端时(模型1), 缓倾断层的反转量最大;当陡倾断层远离挤压端且其倾向指向挤压端时(模型1和5), 无论靠近挤压端的缓倾断层倾向如何,陡倾断层未发生反转; 当缓倾断层远离挤压端且倾向指向挤压端时(模型2和6), 无论靠近挤压端的陡倾断层的倾向如何, 缓倾断层的反转量基本相同。
3.2 先存断层与挤压端的距离对反转构造的影响
本文模拟结果显示了先存断层距离挤压端的位置对其反转量有更明显的影响。Marques and Nogueira (2008)和闫淑玉等(2016)的物理模拟结果也指出, 多个先存正断层存在时, 远离挤压端的正断层也可以反转, 挤压端与先存正断层之间距离对反转构造样式具有明显的影响, 挤压端距离早期正断层越远, 反转背斜核部离早期正断层越近, 反之越远。因而, 本文测试了先存断层与挤压端的距离对模拟结果的影响。模型1~6中, 靠近挤压端的先存断层F2距离挤压端的距离为40 m。在模型2的基础上, 进一步设计了靠近挤压端的先存断层F2与挤压端的距离分别为50 m和60 m的模型7和模型8, 并将其模拟结果与模型2进行对比。
模拟结果表明, 当模型中包含的两先存断层同倾、且陡倾断层更靠近挤压端时, 在先存断层与挤压端距离改变的情况下, 模型内反转构造变形过程及两先存断层反转量的变化趋势均相同(图14、15)。在挤压初期, 两断层同时发生反转, 且两断层的反转量随着压缩率的增大而增大; 在挤压中后期, 靠近挤压端的陡倾断层上部地层反转速率增大, 反转量远远大于远离挤压端的缓倾断层的反转量(图15)。对于模型中包含两条同倾且倾向指向挤压端的模型, 先存断层距离挤压端的距离对远离挤压端的断层F1反转量影响不大, 而靠近挤压端的断层F2随着其距离挤压端距离的增大而增大(图16)。在相同的压缩率下, 先存断层F2距离挤压端距离越大的模型中, 其挤压量越大, 因而造成靠近挤压端的先存断层的反转量越大。模拟结果揭示, 同一个模型中, 先存断层距离挤压端越近, 其反转量越大; 在不同模型中, 先存断层与挤压端的距离大小并不会影响反转次序和反转量变化趋势以及反转构造变形的演化。因此, 在挤压端作为边界条件对模拟结果的影响中, 挤压端距离先存断层距离远近的选取是可以忽略。
3.3 与西湖凹陷反转构造对比
西湖凹陷是东海陆架盆地最重要的凹陷之一, 发育了玉泉、花港和龙井3次构造反转运动(张建培等, 2008), 西湖凹陷中发现的油气储量大都与反转构造有关(陈志勇和葛和平, 2003)。在凹陷中, 下部始新统平湖组顶部为大套灰色泥岩。上部始新统平湖组、渐新统、中新统各组均为泥沙互层。受龙井运动影响, 早期正断层发生反转。离散元模型较好地再现了塑性层上部不同产状组合正断层的反转过程。
由图17a中的剖面可以看出, 两断层同倾且倾向指向挤压端时, 靠近南东方向挤压端一侧的陡倾断层反转幅度更大, 形成更高幅度背斜, 远离挤压端一侧的缓倾断层反转相对较弱。模型2中在挤压后期也再现了两先存断层同倾且陡倾断层靠近挤压端时的反转构造发育情况(图17b)。对比离散元模型2的模拟结果与QY2地震剖面, 均可以发现靠近挤压端一侧的陡倾断层F2反转量更大且发育更高幅度背斜。
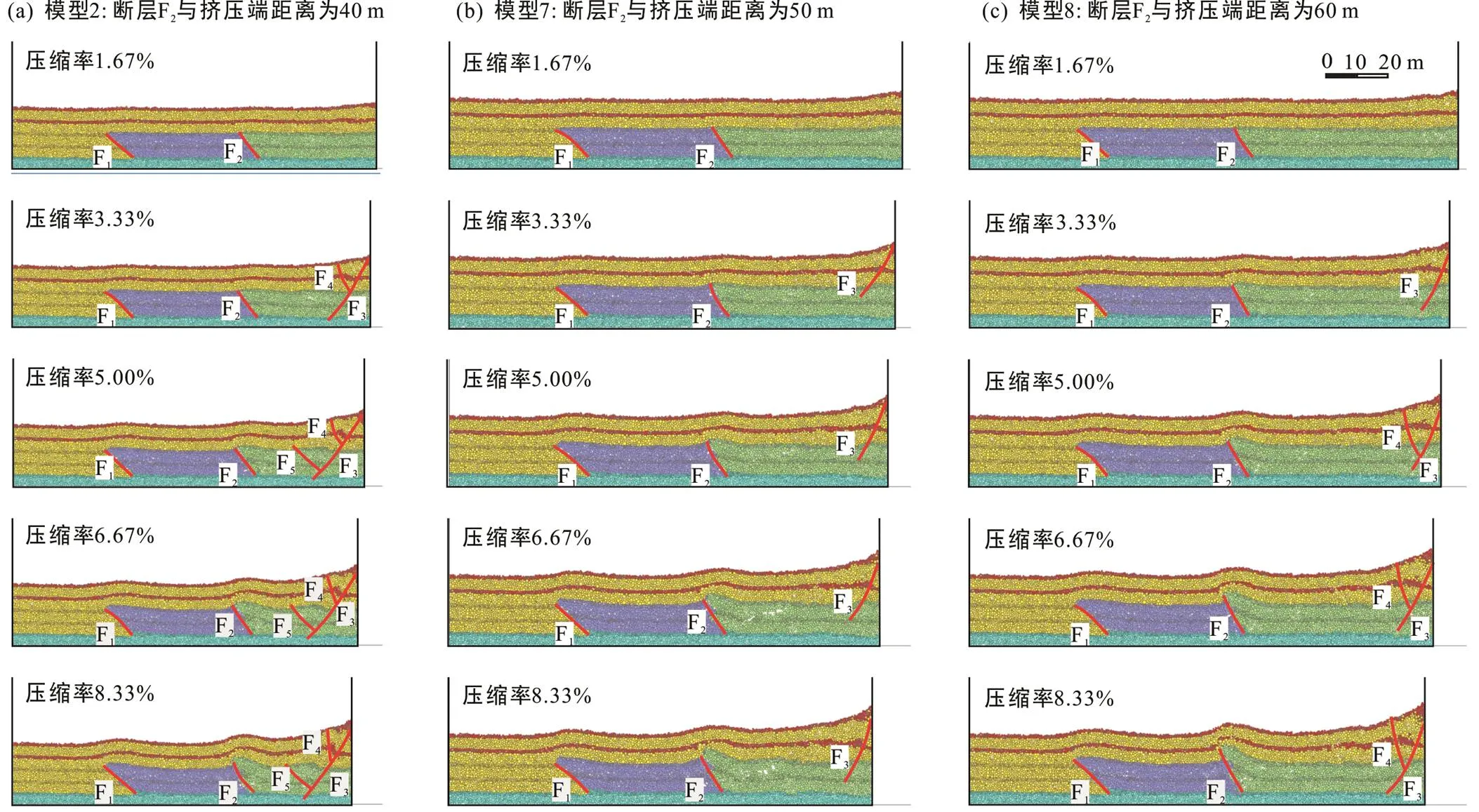
图14 先存断层与挤压端不同距离的离散元数值模型变形过程解释图

图15 模型中同倾断层F1(45°)和F2(60°)Y方向位移随压缩率变化图
由图18a中的剖面可以看出, 两断层对倾且陡倾断层靠近挤压端时, 靠近南东方向挤压端一侧的陡倾断层F2反转幅度更大, 形成较高幅度背斜, 远离挤压端一侧的缓倾断层F1发生微弱反转。模型6中在挤压后期也再现了两先存断层对倾且陡倾断层靠近挤压端时的反转构造发育情况(图18b)。对比离散元模型6的模拟结果与西湖凹陷垂直于反转构造带走向的实际地质剖面, 均可以发现靠近挤压端一侧的陡倾断层F2反转量更大且发育高幅度背斜, 两者有很好的吻合性, 进一步验证了模型的可靠度。
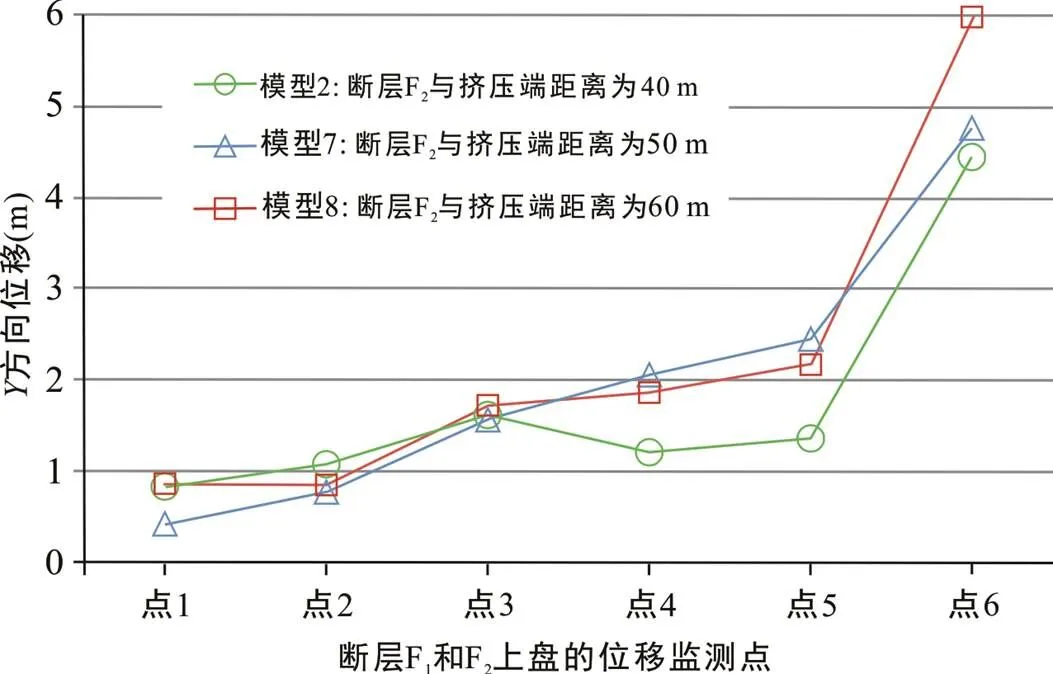
图16 先存断层距离挤压端距离不同的模型中Y方向位移对比图
4 结 论
本文通过离散元颗粒流方法模拟了基底先存正断层的反转变形过程, 研究了陡缓程度、倾向组合关系和距离挤压端位置等因素对先存正断层的反转构造发育及其反转量的影响规律。模拟结果显示, 先存正断层的陡缓程度和倾向组合关系对其反转过程中反转次序、反转量及盖层内断背斜构造的形成有重要影响。
(1) 当先存正断层倾向指向挤压端时, 若缓倾正断层靠近挤压端, 则其上盘形成隆起幅度较大的背斜, 而远离挤压端的陡倾断层未发生反转; 若陡倾断层靠近挤压端, 则缓倾断层和陡倾断层同时发生反转。
(2) 当先存正断层倾向背离挤压端时, 无论靠近还是远离挤压端, 缓倾断层和陡倾断层均发生反转。若缓倾断层靠近挤压端, 则缓倾断层上盘形成隆起幅度更大的背斜; 若陡倾断层靠近挤压端, 则挤压初期, 缓倾断层因倾角小而有较大的反转量, 挤压后期, 陡倾断层反转量快速增加, 反超了远离挤压端的缓倾断层的反转量。

(a) 西湖凹陷北部地区QY2剖面(据宋小勇等, 2010); (b) 模型2模拟结果(压缩率8.33%)。

(a) 西湖凹陷中央反转带对倾断层反转剖面; (b)模型6模拟结果(压缩率8.33%)。
(3) 当先存正断层倾向相对(地堑)时, 若缓倾正断层更靠近挤压端, 则缓倾断层发生明显反转, 而陡倾断层未发生反转; 若陡倾正断层靠近挤压端, 缓倾断层和陡倾断层同时发生反转, 挤压初期, 缓倾断层由于倾角小有较大的反转量, 挤压后期, 陡倾断层由于其距离挤压端距离近, 反转量反超了缓倾断层。
(4) 本文还验证了挤压端作为边界条件对模拟结果的影响, 结果显示, 挤压端距离先存断层的远近对模拟结果并没有影响。同时, 离散元模拟结果与西湖凹陷垂直于反转构造带走向的地震剖面进行对比, 有很好的吻合性, 进一步验证了模型的可靠度。
致谢:感谢南京大学尹宏伟教授和中国石油大学(北京)陈书平教授对文章提出了宝贵的建设性意见, 谨向他们致以最诚挚的谢意!
陈均亮, 李忠权, 应丹琳, 林春华. 2009. 松辽盆地北部白垩纪末反转变形的三维构造物理模拟. 地质科学, 44(1): 63–73.
陈志勇, 葛和平. 2003. 西湖凹陷反转构造与油气聚集. 中国海上油气(地质), 17(1): 20–24.
马宝军, 漆家福, 于福生, 杨雪. 2006. 施力方式对半地堑反转构造变形特征影响的物理模拟实验研究. 大地构造与成矿学, 30(2): 174–179.
宋小勇, 储呈林, 芮志峰. 2010. 东海盆地西湖凹陷构造样式及其演化. 高校地质学报, 16(1): 86–93.
吴珍云, 尹宏伟, 汪伟, 杜业波. 2018. 乍得Bongor盆地反转构造特征及形成机制: 来自地震剖面及沙箱模拟实验的证据. 高校地质学报, 24(6): 918–929.
辛文, 陈汉林, 安凯旋, 张欲清, 杨树锋, 程晓敢, 林秀斌. 2020. 基于离散元数值模拟的西南天山山前冲断带构造变形控制因素研究. 地质学报, 94(6): 1704–1715.
徐雯峤, 汪伟, 尹宏伟, 贾东, 李长圣, 杨庚兄, 李刚. 2020. 库车坳陷东西段盐下构造变形差异演化数值模拟分析. 地质学报, 94(6): 1740–1751.
徐子英, 孙珍, 周蒂, 张云帆, 孙龙涛, 赵中贤. 2012. 软弱地质体对反转构造变形制约作用的物理模拟及其应用. 热带海洋学报, 31(3): 144–154
闫淑玉, 吴景富, 赵志刚, 漆家福. 2016. 西湖凹陷反转构造物理模拟研究. 科学技术与工程, 21(16): 166–176.
张建培, 张涛, 刘景彦, 戴林, 李键, 漆滨汶. 2008. 西湖凹陷反转构造分布与样式. 海洋石油, 28(4): 14–20.
周易, 于福生, 刘志娜. 2019. 分层伸展叠加变形二维离散元模拟. 大地构造与成矿学, 43(2): 213–225.
Adel R M. 2014. Structural architecture and tectonic evolution of the Maghara inverted basin Northern Sinai Egypt., 62: 80–96.
Brun J P, Nalpas T. 1996. Graben inversion in nature and experiments., 15: 677–687.
Buchanan P G, Mcclay K R. 1991. Sandbox experiments of inverted listric and planar fault systems., 188: 97–115.
Buchanan P G, Mcclay K R. 1992. Experiments on basin inversion above reactivated domino faults., 9: 486–500.
Cheng Y M, Liu Z N, Song W D, Au S K. 2009. Laboratory test and particle flow simulation of silos problem with nonhomogeneous materials., 135(11): 1754–1761.
Cundall P A. 1971. A computer model for simulating progressivelarge scale movements in blocky rock systems., 12: 128–132.
Cundall P A, Strack O D L. 1979. A discrete numerical model for granular assemblies., 29(1): 47–65.
Imbera J, Tuckwell G W, Childsa C, Walsh J J, Manzocchi T, Heath A E, Bonson C G, Strand J. 2004. Three- dimensional distinct element modeling of relay growth and breaching along normal faults., 26(10): 1897–1911.
Liu Z, Koyi H A. 2013. The impact of a weak horizon on kinematics and internal deformation of a failure mass using discrete element method., 586: 95–111.
Martínez F, Montanari D, Ventisette C D, Bonini M, Corti G. 2018. Basin inversion and magma migration and emplacement: Insights from basins of northern Chile., 114: 310–319.
Marques F O, Nogueira C R. 2008. Normal fault inversion by orthogonal compression: Sandbox experiments with weak faults., 30: 761–766.
Panien M, Schreurs G, Pfiffner A. 2005. Sandbox experimentson basin inversion: Testing the influence of basin orientationand basin fill., 27: 433–445.
Ren X H, Wang H J, Zhang J X. 2012. Numerical study of AE and DRA methods in sandstone and granite in orthogonal loading directions., 5(1): 93–104.
Smith S A F, Tesei T, Scott J M, Collettini C. 2017. Reactivation of normal faults as high-angle reverse faults due to low frictional strength: Experimental data from the Moonlight Fault Zone, New Zealand., 105: 34–43.
Strayer L M, Suppe J. 2002. Out-of-plane motion of a thrust sheet during along-strike propagation of a thrust ramp: A distinct element approach., 24(4): 637–650.
Ventisette C D, Montanari D, Sani F, Bonini M. 2006. Basin inversion and fault reactivation in laboratory experiments., 28(11): 2067–2083.
Yin H W, Zhang J, Meng L S, Liu Y P, Xu S J. 2009. Discrete element modeling of the faulting in the sedimentary cover above an active salt diapir., 31(9): 989–995.
Zhao C B, Hobbs B E, Ord A, Robert P A, Hornby P, Peng S L. 2007. Phenomenological modeling of crack generation in brittle crustal rocks using the particle simulation method., 29(6): 1034–1048.
Discrete Element Modelling of the Impacts of Attitudes and Geometric Parameters of Pre-existing Faults on Inversion Structures
SUN Qianqian1, 2, LIU Zhina1, 2*, YU Yixin1, 2, TANG Xianjun3, CHEN Shi1, 2, PENG Hao1, 2
(1. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China; 2. College of Earth Sciences, China University of Petroleum, Beijing 102249, China; 3. CNOOC China Limited, Shanghai Branch, Shanghai 200335, China)
Inversion structures are widely developed in China’s marine and continental basins, which are of great significance for oil and gas exploration. Using discrete element modeling, we investigated the influence of dip angles, dip directions and relative distances between pre-existing faults and the shortening boundary on the formation of inversion structures. The modelling results show that these factors have a great impact on the inversion order, inversion amount, and the kinematics of the inversion structures. When the pre-existing normal faults dip towards the shortening boundary, if the gently-dipping normal fault is closer to the shortening boundary, the inversion structures are mainly developed along the gently-dipping fault instead of the steeply-dipping fault; if the steeply-dipping fault is closer to the shortening boundary, the inversion structures are developed along both the steeply-dipping and the gently-dipping faults. When the pre-existing normal faults dip away from the shortening boundary, the inversion structures are developed along both the steeply-dipping and the gently- dipping faults, independent of the distance between the pre-existing fault and the shortening boundary. When the two pre-existing faults are dipping towards each other, the inversion structures are mainly developed along the gently-dipping fault instead of the steeply-dipping fault in the model containing a gently-dipping normal fault closer to the shortening boundary; the inversion structures are developed along both the steeply-dipping and the gently-dipping faults in the model containing a steeply-dipping fault closer to the shortening boundary. In models where both the gently-dipping and the steeply- dipping faults are inverted, the fault closer to the shortening boundary has a larger amount of inversion. The similarity between the modelling results and the seismic section in the central inversion zone of the Xihu Depression further demonstrates that the fault closer to the shortening boundary has larger amount of inversion.
discrete element method; inversion structure; attitude of preexisting faults; inversion order; Xihu Depression
2020-06-28;
2020-09-17
国家自然科学基金项目(42072149)资助。
孙倩倩(1996–), 女, 硕士研究生, 构造地质学专业。E-mail: 13720014030@163.com
刘志娜(1982–), 女, 副教授, 主要从事构造地质学与构造物理研究。E-mail: zhina.liu@cup.edu.cn
P628.3
A
1001-1552(2022)01-0022-014

