基于禁忌搜索的混合储能辅助电网AGC策略研究

王炜，李政，刘宏伟 ，纪项钟，郑楠，于广亮，康健

（1.国网陕西省电力公司经济技术研究院，陕西 西安 710001；2.华北电力大学电气与电子工程学院，北京 102200；3.华北理工大学电气工程学院，河北 唐山 063000）

电网的频率调节的任务主要由自动发电控制（automatic generation control，AGC）系统承担。AGC系统通过获取电网的运行参数（如负荷扰动，频率偏差等）并进行分析处理，求解出区域控制偏差（area control error，ACE），并将ACE根据分配因子分别下发至各调频资源以调整其出力，完成电网频率的控制[1]。由于储能系统具有响应快、控制精确和双向出力的特点，可以瞬间跟踪功率指令，已有越来越多的研究证实了将储能系统作为调频资源加入到电网的AGC系统中来辅助调频的可行性和优越性[2-4]。

将储能系统作为调频资源有单一储能和混合储能两种形式，目前的研究普遍采用蓄电池单一储能的形式[5-10]，并已取得了一些成果。文献[5-7]没有考虑蓄电池储能（battery energy storage system，BESS）荷电状态（state of charge，SOC），虽然简化了分析过程，但是不符合实际运行情况。文献[8-10]将SOC管理纳入优化目标，调节效果较好，但其在应对高频小幅度频率波动时选择采用BESS频繁充放电来进行调节，没有考虑BESS充放电切换带来的电量损失和蓄电池寿命损耗问题。随着BESS参与自动发电控制的研究不断深入，其难以兼顾荷电状态管理和充放电成本的问题日益突出。相对于单一的储能，将多种储能组合起来能够优势互补。目前有文献将超导磁储能与蓄电池结合起来构成混合储能系统来参与AGC控制[11]。但超导磁储能装置成本很高，部分关键设备没有实现国产化，失超保护等部分关键技术没有深入研究和解决[12]。超级电容器是近年来受到国内外研究人员广泛关注的一种新型储能元件，其技术发展较成熟，具有功率密度高，能量密度低的特点[13]，可以快速响应高频小幅度的频率波动，与蓄电池刚好相反。文献[14]将超级电容器与蓄电池结合起来构成混合储能系统，并以ACE所处区间决定其分配原则，大幅度提高了储能系统的功率、能量控制能力，但该策略没有考虑混合储能系统的容量限制，仅验证其对于频率调整的效果，实用性不强。本文采用基于超级电容和蓄电池构成的混合储能系统作为辅助调频系统，同时兼顾考虑SOC和充放电成本，使其更具有实用价值。

为了将混合储能应用于自动发电控制系统中，尚需确定如何实现储能系统和常规机组之间二次调频功率的合理分配，即前文提到的区域控制偏差ACE的分配方式。目前普遍采用动态比例[9-11]的方式，即根据电网和各调频资源运行情况，动态调整ACE在各调频资源间的分配，以取得最优的调节效果。因此本文也采用动态比例的方法对ACE进行优化分配。

综上所述，本文提出了一种由超级电容器和蓄电池构成的混合储能系统参与AGC的控制策略。为了兼顾考虑SOC和充放电成本，以ACE作为输入量，采用频率调节效果好、储能SOC处于最优区间、充放电切换次数少的多优化目标，对ACE在各调频资源间的分配系数进行动态调整。同时采用局部搜索精度较高的自适应连续禁忌搜索（tabu search，TS）算法，保证了该策略的控制效果。通过仿真对比验证了该控制策略的可行性和有效性。

1 含混合储能系统的电网频率控制模型

本文以单区域电力系统为例进行研究，区域内含有一台具备一次、二次调频能力的火电机组以及集中负荷，同时加入了负荷扰动和风电扰动作为功率扰动输入。图1描述了含超级电容器和蓄电池混合储能系统的自动发电控制系统模型[11]。

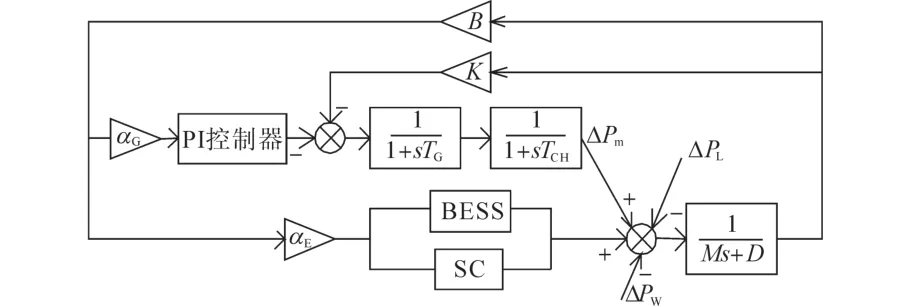
图1 含混合储能系统的自发电控制系统模型Fig.1 AGC system model with hybrid energy storage system

图1中，αG和αE分别为区域中火电机组和混合储能系统的ACE分配系数；K为火电机组单位调节功率系数；B为频率偏差因子；TG为调速器时间常数；TCH为发电机时间常数；M为集中负荷的时间惯性常数；D为集中负荷的阻尼常数；ΔPL为负荷扰动；ΔPW为风电功率扰动；ΔPm为常规发电机机输出功率改变值。BESS和SC分别代表蓄电池和超级电容器储能系统。控制系统通过计算分析得出ACE，再利用自适应连续禁忌搜索算法对分配系数进行动态优化，各调频资源根据自动发电系统控制指令调整自身的出力，最终实现火电机组和混合储能系统的协同调频。

图2为图1中的BESS传递函数模型[15]。该模型分为如下环节：功率转换系统（power conversion system，PCS）、响应延时-时间转换、输出判断以及电池储能设备模型。

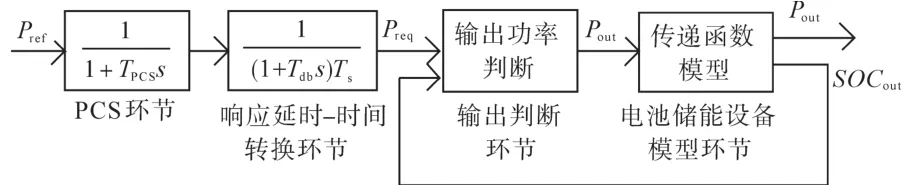
图2 蓄电池传递函数模型Fig.2 Transfer function model of BESS

图2中，Pref为功率参考出力值，正值表示BESS向电网充电，负值表示BESS向电网放电；Preq为经过PCS和响应延时环节后的功率需求；Tpcs和Tdb为别为PCS环节和响应延时-时间转换环节的时间常数；Ts为表示仿真时间与实际时间关系的转换系数；Pout为BESS的实际输出功率；SOCout为储能系统荷电状态量。

图3为图1中超级电容器的传递函数模型[14]。

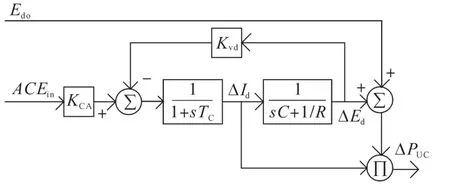
图3 超级电容器传递函数模型Fig.3 Transfer function model of super capacitor

图3中，ΔId为超级电容器电流变化量；Edo为超级电容器电压变化量；ΔPUC为超级电容输出功率的变化量；TC为时间常数；KCA为以ACEin为输入时的控制增益；Kvd为电压控制增益；R为等效电阻；C为等效电容。

为了减少蓄电池的充放电损耗，延长蓄电池寿命，并且最大化利用超级电容器的快速充放电特性，本文设计混合储能系统内部采用由超级电容器优先进行充放电，蓄电池对超级电容器承担不了的爬坡功率进行补充的控制策略[16]。

2 混合储能系统参与自动发电控制的多目标优化模型

混合储能系统参与AGC控制的关键步骤是确定ACE在混合储能系统中的分配系数αE，需要同时兼顾调频效果，蓄电池SOC状态和充放电次数多个优化目标，属于多目标优化问题。控制总目标为使得解向量的标准化满意度h最大，优化模型如下6式。

式中：hi为第i个解向量的标准化满意度；N为目标函数的数量。

可用式（1）求取解空间中所有解向量的标准化满意度。

式中：Ci为各目标函数值；分别为第i个目标函数的最大值和最小值。

式（2）表示解集中每个解向量的各目标函数所对应的满意度的模糊隶属度函数[17]。

式中：CPS1为美国电力可靠性协会（NERC）提出的CPS标准中的CPS1指标变量；ACE1min为区域控制偏差的1 min平均值，单位为MW；Δf1min为系统频率偏差的1 min平均值，单位为Hz；Bcps为系统的频率响应系数，单位为MW/Hz；ε1为电网1 min平均频率偏差的控制目标值，本文取0.022 Hz[18]。

式（4）为频率偏差目标函数，本文采用CPS1考核自动发电控制系统的调频效果。因此，C1越小，表明系统的CPS1指标CPS1数值越大，电网的频率控制性能越好。

式中：SOCavg为一个采样周期内SOC的平均值。

式（5）为SOC状态目标函数，在混合储能系统参与调频的过程中，需要保持BESS的SOC在40%～60%的理想区间中，以延长储能设备的工作寿命，并保证足够的调频容量储备。由式（5）可知，C2的值越小，BESS的SOC越接近理想区间，SOC状态就越好。

式中：T为总考核时间段数；t为采样时间段；uch.t为1表示BESS在t时段内由放电状态转换为充电状态，udis.t为1表示BESS在t时段内由充电状态转换为放电状态，当BESS的充放电状态没有切换时两者均为0。

式（6）为充放电成本目标函数[19]，因此，C3的物理含义为在考核时间段内BESS的充放电状态切换次数。C3的值越小，BESS在考核时间段内的充放电次数就越少。

3 算法设计

3.1 自适应禁忌搜索算法简介

禁忌搜索是一种现代启发式算法，是局部邻域搜索的一种扩展。将其应用到连续优化问题的求解中，即为连续禁忌搜索算法。算法每次迭代时在初始解的邻域中随机生成若干个候选解，初始解与候选解共同构成该次迭代的解集。在迭代寻优的过程中，禁忌搜索算法可以标记已搜索的局部最优解，并在进一步的迭代中避开这些对象，从而保证对不同的有效搜索途径的探索，被标记的局部最优解的集合即为禁忌表。

禁忌搜索算法有两个关键属性，即集中性和多样性。集中性强调的是在对当前搜索到的优良解的邻域作进一步的纵向搜索，以期达到足够的搜索深度以实现局部的最优。而多样性则强调跳出目前的搜索区域，扩大搜索方向，避免陷入局部最优。为此本文采用自适应禁忌搜索算法[20]，通过对候选集的动态调整较好地解决集中性和多样性的矛盾，即将候选集分为两个部分，前半部分代表集中性元素，后半部分代表多样性元素。设候选解集合的长度为CL，候选集中集中性元素的个数记为DL。在迭代搜索过程中，DL按以下规则动态变化：若本次迭代搜索到的当前局部最优解优于前一步迭代的局部最优解，则DL自动加1，否则DL自动减1。DL的取值范围为[1，CL-1]，即候选集在迭代过程中始终同时包含集中性元素和多样性元素。

3.2 基于自适应禁忌搜索算法的ACE配置优化

定义ACE分配给混合储能部分的分配系数αE为待优化量x1，基于自适应连续禁忌搜索算法的ACE配置优化的关键参数设置为：

1）确定x1的取值范围和初始值。假如ACE为正，系统中出现功率缺额的时候，综合考虑前述三个控制目标，如果此时储能系统为了调整SOC和减少充放电次数而吸收功率，同时能够兼顾频率控制，这种情况下x1即可为负值；因为混合储能系统所接收到的ACE数值占ACE总值的比例从0到100%，因此x1的取值范围为[-1，1]。x1的初始值为在可行区间[-1，1]内随机产生的一个数值。

2）确定邻域的选取范围。采用[a-δ，a+δ]边界移动法[a-δ，a+δ]确定初始解的邻域[21]，a为该次迭代的初始解，δ为一个很小的常数，其值根据经验选取，在后续仿真验证中δ取0.03，效果较好。

3）确定候选集长度CL、集中性元素个数DL初始值。CL的值根据经验选取，在后续仿真验证中CL取10，效果较好，DL=CL/2=5，即集中性元素和多样性元素各占一半。

禁忌表长度定义禁忌表的长度根据经验选取，本文中取10，δ为0.03。若某个解与禁忌表中解的差值的绝对值小于δ，则视该解为禁忌状态，将其加入到禁忌表中。

基于自适应连续禁忌搜索算法的ACE配置优化的具体优化步骤为：

1）初始解及其邻域，在其邻域内产生若干候选解，构成解集U0，候选解通过随机的方法产生。

2）将ACE值和U0中的解依次代入运行。通过式（3）～式（6）计算出各项目标函数值。

3）检验是否满足特赦准则：对U0中各个解的目标函数值进行排序，求出其中的最优解，若该解集最优解为该次迭代的候选解，则将其作为下次迭代的初始解。若解集最优解为初始解x1，则分两种情况讨论，若x1优于全局最优解，则更新全局最优解，并将其作为下次迭代的初始解。否则将其加入到禁忌表中，任期设置为10，对DL参数进行更新，并对下次迭代的初始解进行随机选取。

4）进行下一步迭代，在新的初始解的邻域中随机生成候选解构成该次迭代的解集，判断各个解的禁忌属性：若某个解与禁忌表中的解的差值的绝对值小于δ，则将该解加入到禁忌表中，同时将禁忌表中其余解的任期依次减1，任期为0的解移出禁忌表。将处于非禁忌状态的解依次代入模型中进行仿真运行，同时将全局最优解代入，求取所有解的目标函数并进行比较。

5）若全局最优解经过30次迭代依然没有改变，则停止迭代，将此时的全局最优解作为该控制区间的αE的最优值，否则返回重新迭代。

算法具体流程如图4所示。

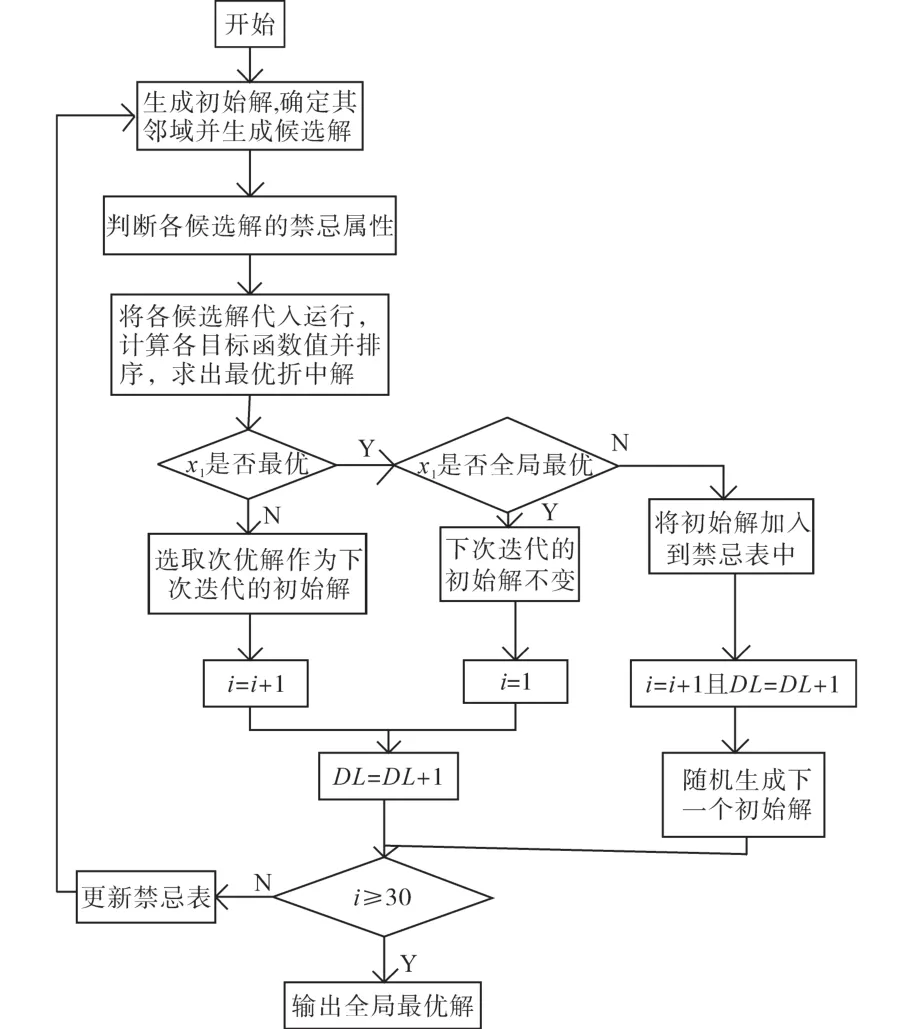
图4 优化控制策略算法流程Fig.4 The flow chart of optimal control strategy algorithm

4 仿真验证

4.1 自适应禁忌搜索算法仿真

为了实现对电网调频的持续优化，引入滚动优化的方式，即对未来1 min的ACE分配系数进行优化计算，并将优化结果作为初始值，继续进行下一控制区间的优化，将滚动优化与上述禁忌搜索算法相结合实现分配系数的动态优化。在Matlab/Simulink中搭建如图1所示的含混合储能的自动发电控制系统模型。功率基准值选取为1 000 MW，频率基准值为50 Hz。其中火电机组装机容量为400 MW，参数为：K=20，TG=0.2 s，TCH=0.3 s，M=10.0 s，B=40，PI控制器参数选取为：Kp=0.06，Ki=0.03，系统内的BESS的参数为：配置容量为3 MW·h，初始SOC为50%，最大充放电功率为20 MW，Tpcs=0.01 s，Tdb=0 s，Ts=1 s[19]。超级电容器的配置容量为0.5 MW·h，参数为：Edo=2 V，KCA=1，TC=0.05 s，Kvd=0.1，C=1 F，R=0.01 Ω[15]。

为了验证上述禁忌搜索算法的ACE优化配置效果，设置由负荷扰动和风电功率扰动构成的总扰动量，总扰动为阶跃变化的方波，每个控制区间长度设置为60 s。总功率扰动的波形如图5所示。

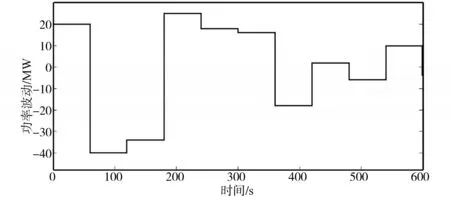
图5 系统所受功率扰动曲线Fig.5 Power disturbance curve of the system

为了验证本文所采用的禁忌搜索算法（后文中简称为TS算法）的优越性，将其与电力系统调度优化常用的遗传算法进行对比分析。基于相同的仿真模型、控制策略、迭代次数和优化目标函数，分别采用禁忌搜索算法和遗传算法，针对图5给出的功率扰动的情况进行仿真计算。采用两种算法分别得到的ACE优化分配系数如表1所示。

观察表1可以发现TS算法求得的结果在第3，5，9和第 10个控制区间，其分配系数αE为负数，说明在这些控制区间内，混合储能系统的出力方向与ACE方向相反。

表1 2种算法各控制时段储能系统分配系数Tab.1 Distribution coefficient of energy storage system in eachcontrol period under the two algorithms

仿真结果的对比如图6～图8所示，分别给出了频率波动曲线、SOC曲线和BESS输出功率曲线。为了方便区分，将TS算法对应的结果用实线表示，遗传算法对应的结果用虚线表示，两种算法对应的结果都是连续变化的。

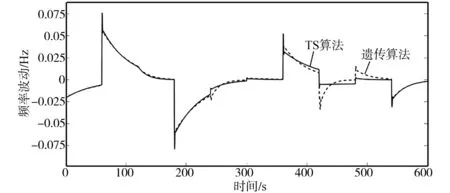
图6 不同算法下频率波动曲线对比Fig.6 Comparison of frequency fluctuation curves under different algorithms

图7 不同算法下BESS的SOC曲线对比Fig.7 Comparison of SOC curves of BESS under different algorithms

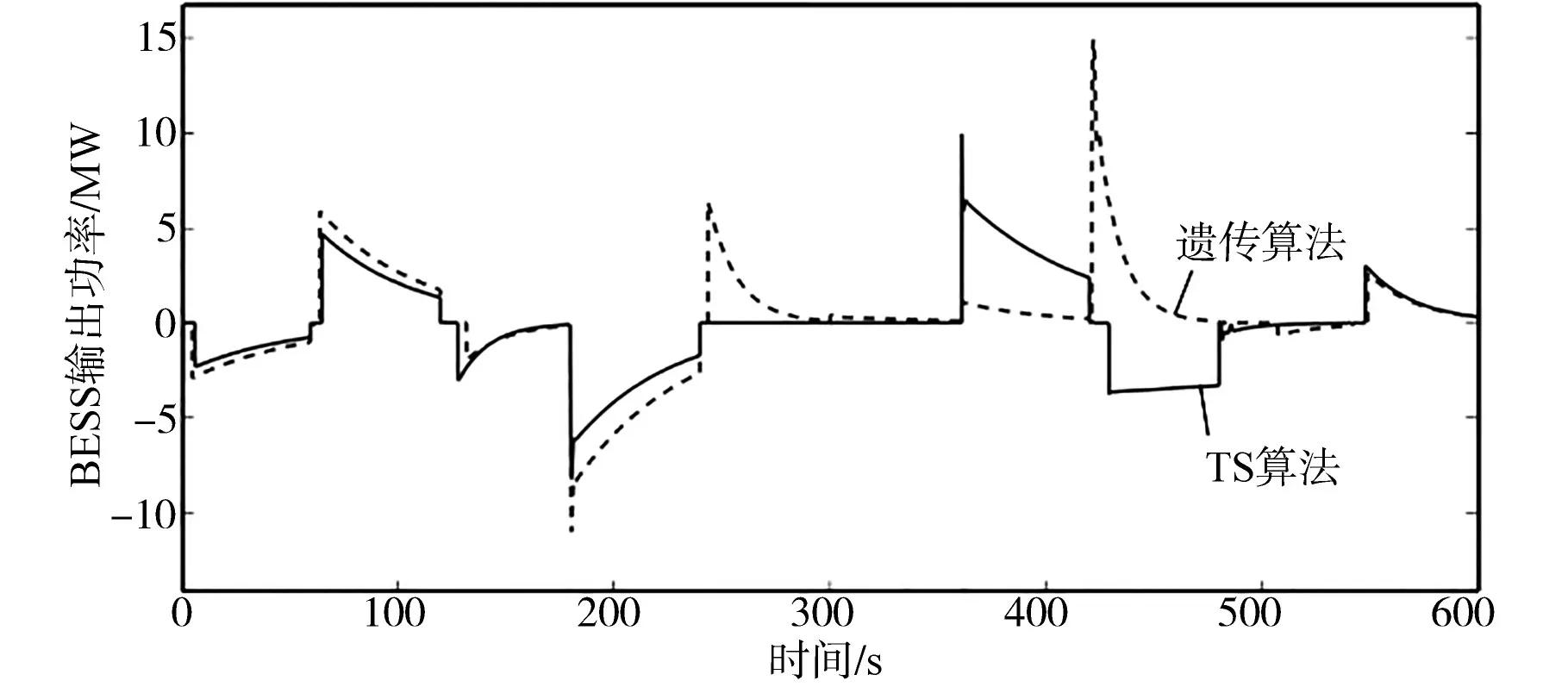
图8 不同算法下BESS输出功率曲线对比Fig.8 Comparison of output power curves of BESS under different algorithms

首先分析不同算法对频率波动和SOC的影响。在0～180 s以及300～420 s这两个控制区间内，由图6和图7可知，两种算法下频率波动近似，SOC均在40%～60%的理想区间。在180～240 s这个控制区间内，由图6可知两种算法下频率波动近似，由表1可知，TS算法求得的分配系数0.130比遗传算法的系数0.183小，相当于减少了BESS的充电量，因此由图7可知TS算法将BESS的SOC值保持在了40%～60%的理想区间内，而遗传算法对应的SOC值超出了理想区间。在240～300 s，540～600 s这两个控制区间内，两种算法对频率波动和SOC的影响结果与180～240 s这个控制区间相同。在420～480 s这个控制区间内，两种算法均使得SOC保持在了理想区间内，但是观察图6可以看出TS算法明显降低了频率波动的峰值。在480～540 s这个控制区间内，两种算法对频率波动和SOC的影响结果与420～480 s这个控制区间相同。

然后分析不同算法对BESS的充放电切换次数的影响。图8给出了BESS输出功率的波形，结合表1可知，在240～300 s这个控制区间内，TS算法求得的分配系数-0.117比遗传算法的系数-0.474绝对值小，使得混合储能系统所分配的ACE值可由超级电容器单独承担，BESS输出功率为0，免于进行充放电切换。在420～480 s这个控制区间内，由图8可知TS算法情况下有一次充放电切换，即输出功率由正到负，而遗传算法情况下无充放电切换，与图6交叉对比可知，TS算法使得此控制区间内频率波动的峰值明显降低。在480～540 s这个控制区间内，TS算法求得的分配系数与前一个控制区间符号相反，由于ACE在这两个控制区间符号也是相反的，最终使得BESS没有进行充放电切换，同时并未影响系统的调频效果和BESS的SOC健康。从整体结果来看，不同算法下BESS的充放电切换次数近似相等。

在电力系统的实际运行中，可能会出现未来一段时间的风电功率波动和负荷波动难以预测或无法预测的情况，此时本文所设计的实时优化控制策略因为缺乏输入量而无法运行。为了应对这种情况，本文设计在某一段时间功率波动无法预测时，优化策略停止运行，采用按固定比例的方式对ACE进行分配，分配比例为调频机组与混合储能系统的装机容量之比。当功率波动预测恢复时再启动优化策略控制ACE的分配。为了验证这种控制方式的可行性，采用两种运行工况进行对比分析，工况1是正常工况，全部采用TS算法进行优化，工况2是120～240 s功率波动无法预测的特殊工况，在此期间ACE采用固定比例分配，其余时段采用TS算法优化。为了更好地观察短时按比例分配控制对后续控制效果的影响，将仿真时长设置为1 200 s。仿真结果如图9～图11所示。

图9 两种工况下频率波动曲线对比Fig.9 Comparison of frequency fluctuation curves under two working conditions

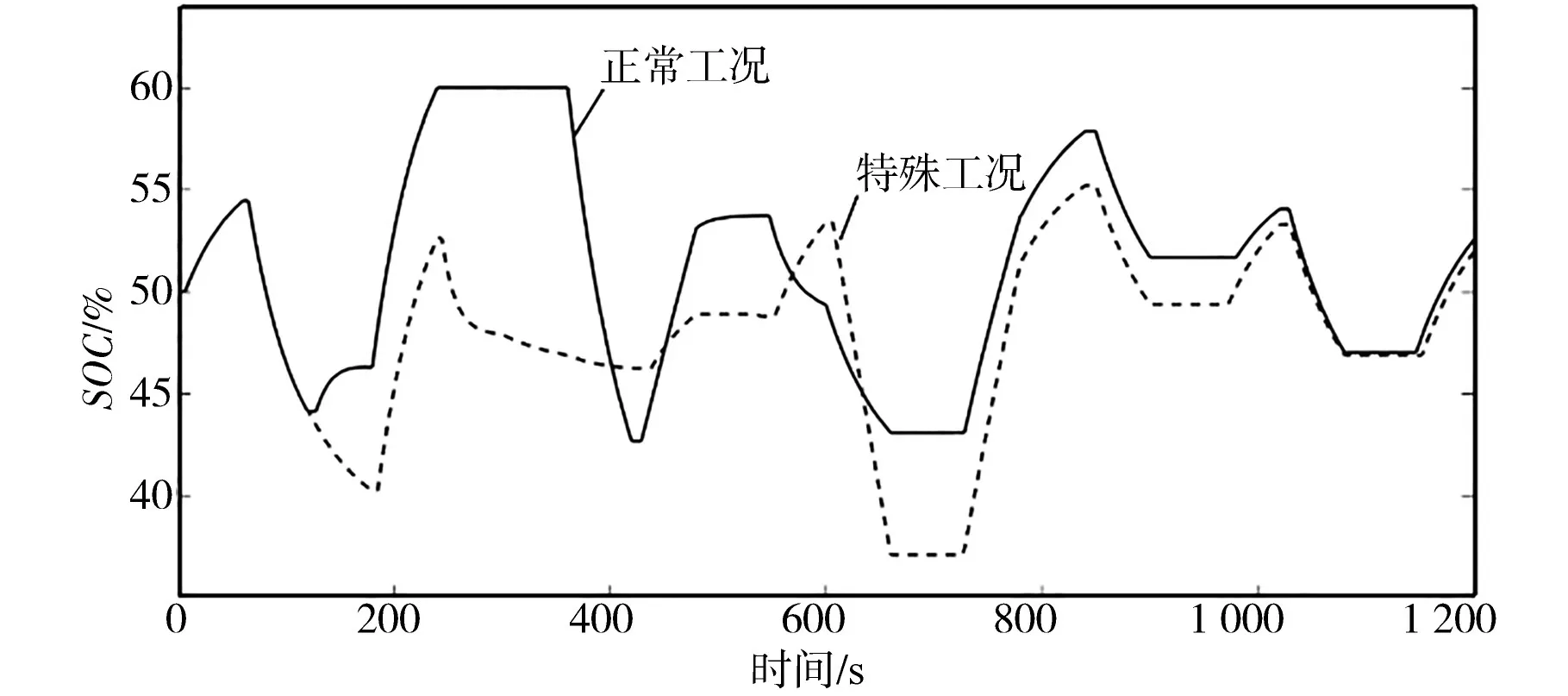
图10 两种工况下BESS的SOC曲线对比Fig.10 Comparison of SOC curves of BESS in emergency under two working conditions

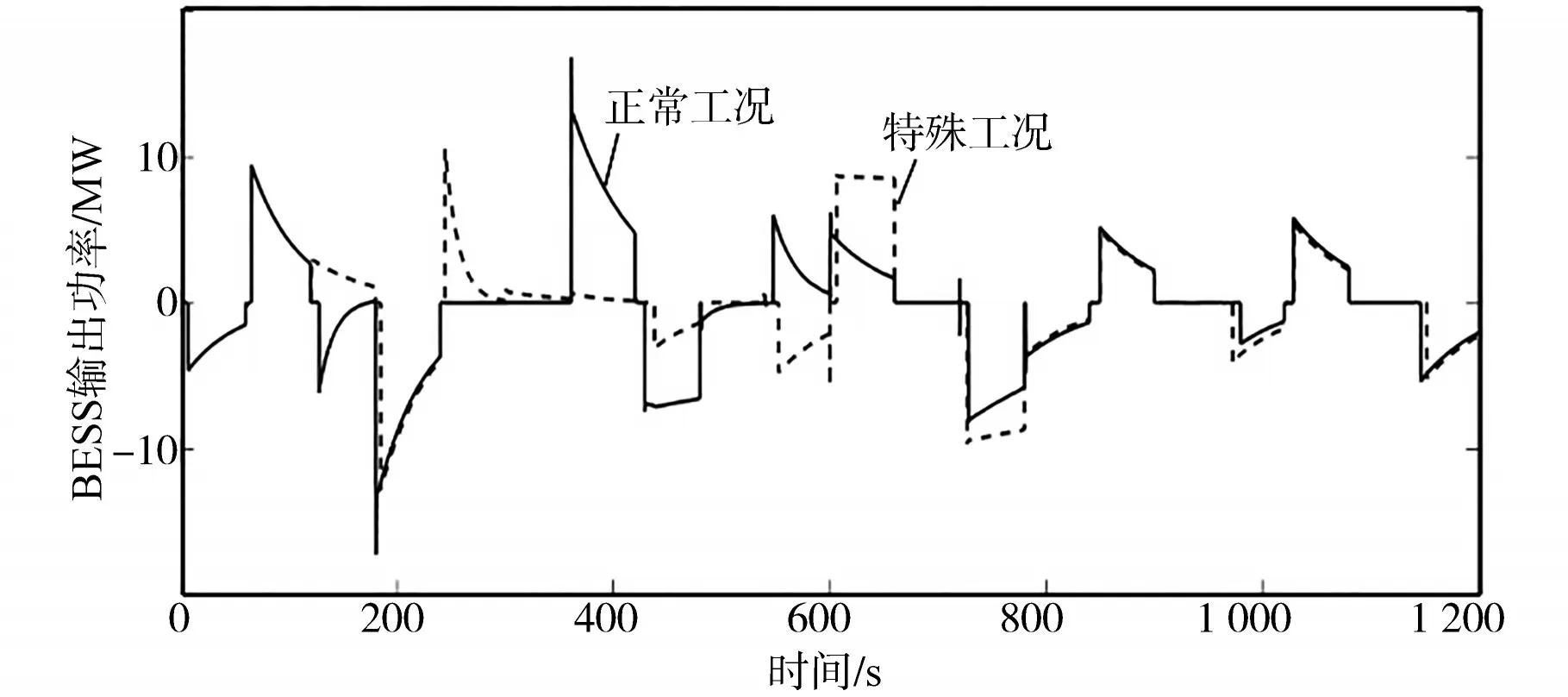
图11 两种工况下BESS输出功率曲线对比Fig.11 Comparison of output power curves of BESS in emergency under two working conditions

从图9～图11中可以看出，在特殊工况中功率扰动无法预测的时间段之后，经过一定的暂态过程，所提出的优化控制策略可以将系统的频率波动，BESS的荷电状态和BESS的出力逐渐恢复到与正常工况相似的水平。

4.2 自适应禁忌搜索算法耗时

为了保证本优化策略中1 min级优化的可行性，需要考虑自适应禁忌搜索算法每个控制区间优化的耗时。本文采用了如下的仿真环境：CPU为 Intel®Core™i7-9750H@2.60 GHz，内存为 16 GB，操作系统为Windows，仿真平台为Matlab。经过大量的仿真实验，得出对应仿真环境下平均计算时间为35.7 s。可以看出，在常用的个人计算机配置下，自适应禁忌搜索算法对1 min级控制区间的最优解计算时间小于1 min，能够满足实际应用需求。

5 结论

为了实现混合储能系统与常规机组协调参与AGC控制，本文提出了一种基于自适应连续禁忌搜索算法的优化控制策略，对ACE的分配系数进行实时动态优化，并将其与电网优化常用的遗传算法进行对比，仿真结果表明：1）该策略能够有效提高系统频率的稳定性，显著降低其暂态频率波动峰值。2）该策略能够使SOC值保持在理想区间内，为BESS参与调频提供较多的容量裕度。3）在功率波动难以预测或无法预测的时段，采用短时按固定比例分配系数的控制策略具有可行性，从而增强了控制策略的适应性。