基于新型模糊自适应惯量VSG的微网频率波动抑制

王晨丞，蒲丽娟，杜斌，万忠兵，张君胜，赵智辉

（国网四川省电力公司计量中心，四川 成都 610045）

随着社会的不断发展与进步，人们对能源的需求不断增长，然而，传统不可再生能源储量却因此日益减少，这促使以新能源为基础的新一轮能源变革蓬勃兴起[1]。目前，已广泛应用的新能源主要包括风能、太阳能和潮汐能等，通过发电技术可将这些能源转化为电能，进而直接使用或并网传输[2-3]。这些由新能源为基础的发电、供电系统构成微网，由于它们具有地域分散性和容量较小的特点，微网中的发电装置又被称为分布式电源（distributed generation，DG）[4-6]。以DG为核心的微网可工作在孤岛模式或并网模式下，然而，无论何种模式，DG都需要通过逆变器等电力电子变流装置与负载和电网相连，以实现电压和频率调节。电力电子装置的使用令微网具有可控性和响应速度快的优势，但与传统同步发电机相比，其几乎没有转动惯量，且阻尼较小，在负载发生波动时，无法通过自身惯量吸收或释放能量，也无法通过阻尼削弱负载功率变化冲击，导致系统电压与频率波动剧烈，严重时危害电网安全[7]。

为增强系统的频率支撑能力，德国克劳斯塔尔工业大学学者Beck教授早在2007年提出了虚拟同步机（virtual synchronous generator，VSG）的概念，利用控制算法模拟真实同步发电机的运动特性方程，率先使整个微网系统表现出了惯量以及阻尼特性[8]。但最早的VSG控制是将逆变器等效为电流源，属于电流控制型技术，仍然很难直接为系统提供频率支撑。为解决该问题，电压控制型VSG于2011年由美国伊利诺理工大学学者钟庆昌教授提出，通过同步发电机的二阶转子方程以及励磁方程更加精确地模拟出了真实同步发电机的工作特性，并实现了VSG无锁相环同步运行，直接且同时为微网提供频率和电压支撑[9]。在此基础上，电压型VSG技术已经取得了更为广泛的研究，例如，合肥工业大学张兴教授团队不断改进VSG控制策略，在高精度功率分配及电网谐波抑制技术方面做出了重大贡献，提高了电能质量[10-11]；Chandorkar M C教授团队将基于自适应因子的下垂特性调节器与VSG控制器相结合，改善了系统的暂态频率响应[12]。

值得注意的是，从文献[12]可得出以下启示：1）在利用VSG控制技术调节微网频率和电压时，若VSG控制器参数设计不合理，系统性能会受到影响，其中，当虚拟转动惯量比较大时，微网的频率响应速度降低，频率震荡明显且周期加长；2）采用自适应参数可实时改善微网的性能，除采用自适应下垂特性调节器外，也可通过设计自适应VSG控制器获得理想的控制性能。文献[13]利用bang-bang控制器产生实时虚拟惯量提高系统的动态性能，但其固有的抖动问题使得控制精度无法得到保障；文献[14-15]将虚拟惯量计算转化为最优化求解问题，分别利用二阶优化算法和粒子群算法求得最佳实时惯量，在降低频率震荡的同时提高响应速度，但该方法计算复杂，对设计人员要求比较高；文献[16-18]设计了基于模糊自适应控制器的VSG控制技术，通过评估频率和功率偏离额定值的幅度推理获得合理的控制参数，实现方式简单，具有较强的鲁棒性和非线性适应性，值得进一步推广与应用。然而，由目前常用的模糊控制器所产生的自适应惯量在整个模糊区间内变化比较平稳，若设计经验不足，使用中会存在以下问题：当负载功率波动很大导致频率偏差接近最大许可值，模糊控制器的输出仍是缓慢变化，可能由于惯量不足使得无法有效阻止频率进一步偏离，给系统带来风险。

针对上述问题，提出一种基于改进型模糊自适应惯量VSG控制技术以降低微网的频率波动。首先，定义频率偏差界限的概念，并将其融入至模糊控制器设计过程中，其优势体现在当微网频率偏差小于界限值时，模糊控制器输出校正因子取较小值，赋予系统较小的惯量，保证良好的动态性能；当频率偏差超过界限范围，采用较大的输出校正因子，此时，系统获得足够惯量，频率变化率明显降低，避免波动幅值进一步增加，从根本上避免由经验不足引发的不合理惯量设计。最后，利用仿真和实验结果验证了所提控制方案的有效性。

1 VSG控制结构

图1为基于VSG控制的微网系统结构示意图，其中硬件系统主要包括等效为直流电源（Udc）的DG，三相电压源逆变器（输出为Ea，b，c），通过断路器与微电网连接的电网，本地负载，直流和交流滤波电容Cdc和Cf，滤波阻抗Zf，传输电缆（等效电阻和电感为 Rt和 Lt）；三相电压（Ua，b，c）和电流（Ia，b，c）信息通过互感装置测量获得，然后经过锁相环和功率计算模块得到电网实时工作频率f、电压幅值Um、有功功率Pe和无功功率Q[19]；VSG控制算法包含电压调节和频率调节两部分，是VSG控制的核心，其中，电压调节包含Q—V下垂控制器和电压控制器两部分，而频率调节包含f—Q下垂控制器、同步发电机摇摆方程控制器和积分器三部分。由于主要研究VSG控制器设计，本节将对VSG控制算法部分重点介绍，为构建系统扰动模型和控制性能分析奠定基础。

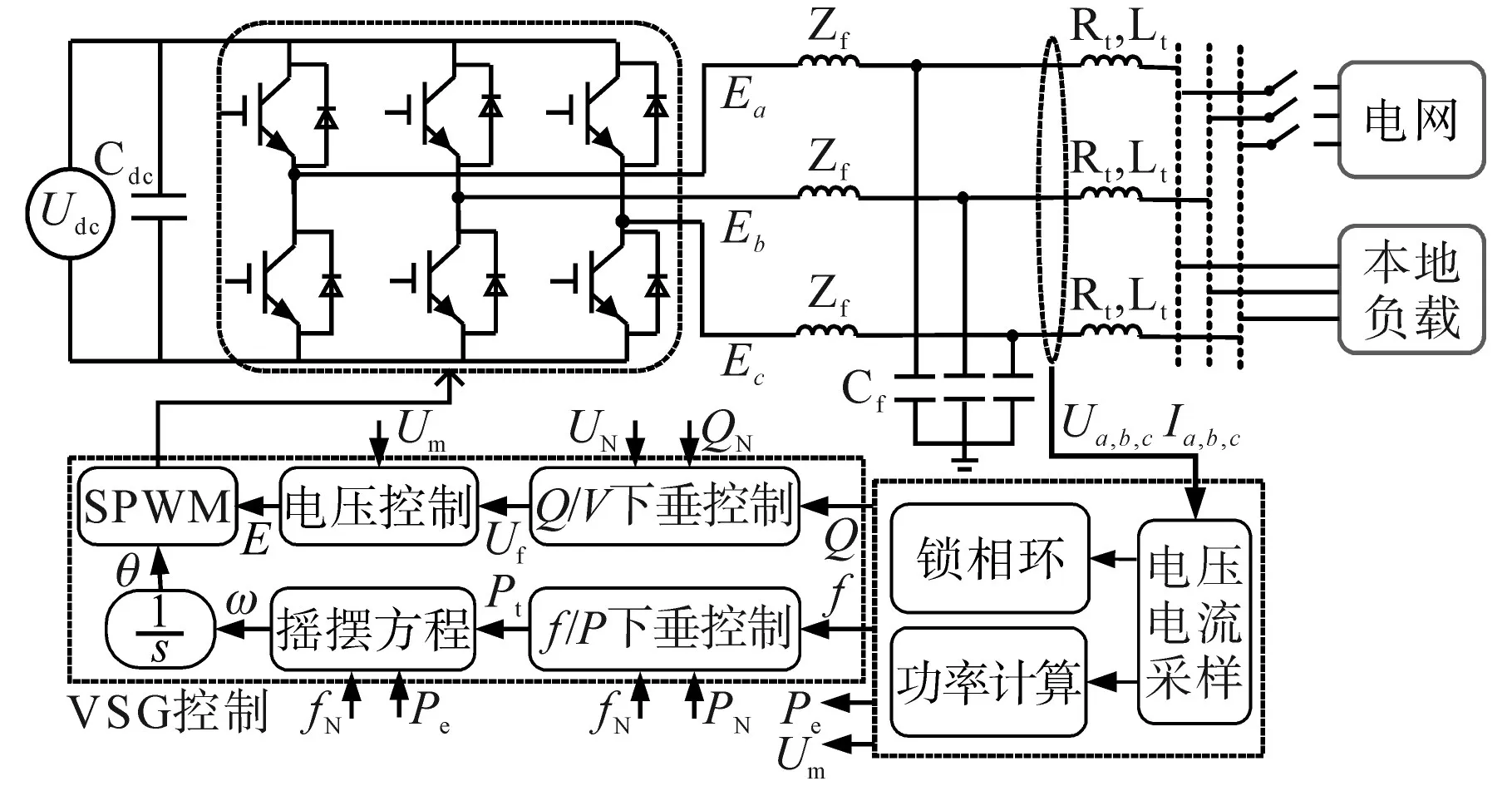
图1 基于VSG控制的微网结构图Fig.1 Structure of microgrid based on VSG control strategy

1.1 Q—V下垂控制

Q—V下垂控制器使得无功功率调节成为整个电压调节环节的内环部分，用来产生参考电压Uf，它是根据同步发电机无功功率-输出电压之间的下垂关系（如图2所示）所建立的模块。

由图2可知，当负载无功功率偏离额定值QN时，微网中的无功功率会随之立即发生改变，当控制逆变器使其输出与负载无功功率重新达到平衡后，逆变器输出电压无法再维持至额定值UN，且当负载无功功率减小时（Q1），电压上升（U1），而当负载无功功率增大时（Q2），电压下降（U2）。定义下垂系数kV为

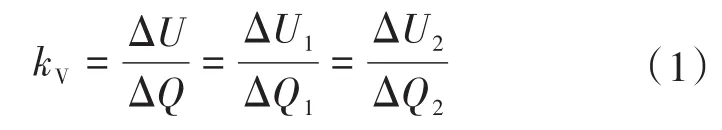
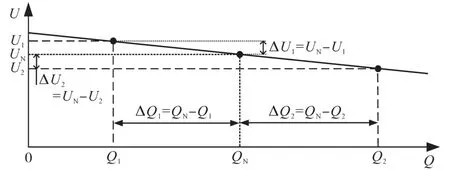
图2 同步发电机无功功率—输出电压下垂关系Fig.2 Droop characteristics of synchronous generator between reactive power and output voltage

式中：ΔU和ΔQ为电压和功率偏差。

显然，kV是负值。根据同步发电机无功功率-输出电压下垂关系可得逆变器输出电压应满足以下关系：

1.2 电压控制

传统的下垂控制直接使用Uf作为产生脉宽调制（pulse width modulation，PWM）信号的参考，该方法的缺点是微网电压没有反馈调节环节，在无功功率发生突变时，电压波动较大。为改善这一缺点，并实现逆变器输出电压对参考值Uf的无差跟踪，采用PI控制器实现电压外环调节，即

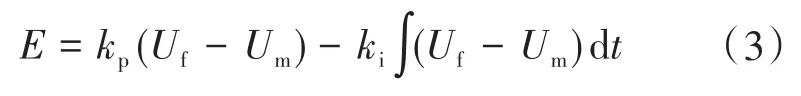
式中：E为PI控制器输出，代表同步发电机反电势，即微网逆变器所需输出电压；kp为比例因子；ki为积分因子。

根据式（2）和式（3）可得电压调节环节结构框图如图3所示。

图3 电压调节环节结构框图Fig.3 Block diagram of voltage regulation loop

1.3 f—P下垂控制

f—P下垂控制器对微网频率进行一次调节，用来计算VSG所需要输出的机械功率Pt，与Q—V下垂控制器一致，它是根据同步发电机有功功率-输出角频率之间的下垂关系所建立的控制器。参照式（2），逆变器输出角频率与有功功率关系为

式中：ω为发电机的工作角频率，满足ω=2πf；ωN为发电机的额定角频率；fN为微网额定工作频率；kf为下垂系数；PN为额定有功功率。

1.4 摇摆方程

同步发电机摇摆方程是VSG控制技术的核心，通过模拟同步发电机的机械特性，将逆变器赋予惯量和阻尼特性，摇摆方程的作用为实现频率二次调节。同步发电机的摇摆方程为

式中：J为虚拟惯量；D为虚拟阻尼；θ为同步电机转子角度。

VSG控制使得电网表现出与同步电机相似的特性，具体为：当负载功率偏离参考值时，功率不平衡会造成频率波动的趋势，即在式（5）中，若Pt-Pe≠0，则ω会发生波动，对于相同的频率偏移ω-ωN，由于惯量J的作用，频率变化率会降低，导致在相同时间内，频率波动量也会下降，这就是虚拟惯量的引入会降低系统频率响应速度却抑制频率波动的原因；另外，由于ω-ωN与Pt-Pe的符号不同，阻尼的引入同样会降低频率变化率，抑制频率波动幅值。

根据式（4）和式（5）可得频率调节环节结构框图如图4所示。

图4 频率调节环节结构框图Fig.4 Block diagram of frequency regulation loop

2 改进型模糊自适应惯量VSG控制

改进型模糊自适应惯量控制器结构如图5所示，其中，Δf=f-fN，为频率偏离额定值大小；Kf和Kfd为输入校正因子；In1和In2为模糊推理机的输入；Out为模糊推理机的输出；J′为解模糊模块的输出；K1和K2（K1＜K2）为输出校正因子；Jadp为自适应惯量，实时应用于VSG控制过程中；fthr为所定义的频率偏差界限。下面详细介绍模糊控制器各部分设计过程。

图5 改进型模糊自适应惯量控制器Fig.5 Improved fuzzy adaptive inertia controller

2.1 模糊化

模糊化的目的是将实际的变量转换为模糊控制可讨论的变量及范围。将微网频率偏差Δf和偏差变化率dΔf/dt作为模糊控制器输入量，为方便计算，借助标幺化的理念，将Δf和dΔf/dt的模糊论域定为[-1，1]，此时，比例输入比例因子为

式中：Δfmax为微网最大许可频率偏差；Δfdmax为最大频率变化率。

我国对于3 000 MW以下的小电力系统的频率偏差规定不得超过±0.5 Hz，因此，Δfmax取0.5；频率变化率可根据经验设计，其取值可能较大，本研究中取Δfdmax=600。模糊化后的输入变量分别定义为In1和In2，用于进行模糊推理。

2.2 模糊控制规则

模糊控制规则是模糊推理的基础，是将模糊控制器输出与输入进行关联的依据。在制定模糊控制规则前，先将模糊推理机的输入“In1”、“In2”及输出“Out”一致采用“正大（PB）”、“正中（PM）”、“正小（PS）”、“零（ZO）”、“负小（NS）”、“负中（NM）”、“负大（NB）”七个语言值来描述。对于输入，由于In1和In2可以是正值也可以是负值，对应的模糊集为{PB，PM，PS，ZO，NS，NM，NB}；但对于输出而言，由于最终虚拟惯量取正值，则对应Out的模糊集为{PB，PM，PS}。表1列出了49条模糊控制规则，由表可以看出：1）当频率偏差很小（ZO）时，即使频率偏差变化率很大，惯量仍采用较小值，保证较快的频率响应速度；2）当频率偏差较大或很大时，若偏差变化率与偏差同号，采用较大惯量，否则，采用较小惯量；3）当频率偏差较小时，即使其与偏差变化率同号，仍采用较小惯量。

表1 模糊控制规则表Tab.1 Fuzzy control rules

2.3 隶属度函数

隶属度函数将模糊论域内的输入值映射为0～1之间的隶属度，选择隶属度函数时必须注意以下问题：1）隶属度函数的分布必须覆盖整个模糊论域；2）相邻两函数之间要存在交集，但不能出现三个隶属度函数相交的情况；3）当两个相邻的隶属度函数之间相交程度大时，模糊控制器鲁棒性好，但灵敏度较低，输出变化更不明显，相反，当相交程度较小时，灵敏度较高，对于电网频率偏差而言，当其较大时，对模糊控制器敏感程度要求更高，因此，所采用的隶属度函数在对应变量取较大值时相交程度减小，如图6所示。

图6 隶属度函数Fig.6 Membership functions

2.4 解模糊

模糊推理机的输出结果并不是一个单值或者一个解析表达式，而是另一个模糊集合，所以需要将输出结果通过解模糊算法转换成单值，为获取准确的控制量，就要求解模糊的方法能够尽可能表达出输出隶属度函数的反应结果。加权平均法具有反应灵敏、操作简单的优点[19]，已在工程中取得了广泛应用，其中，该解模糊方法的实现过程为

式中：m为隶属度函数个数，即模糊集中变量个数，m=3；yi为模糊集中每个变量取值；u（yi）为模糊集中每个变量对应的隶属度。

2.5 考虑频率偏差界限的虚拟惯量设计

当频率偏差很大，且频率偏差变化率与之同号时，频率偏差幅度具有进一步增大的趋势，这时需要很大的惯量以抑制频率波动，维持微网的安全。但对于采用单一输出校正因子的模糊控制器，为保证频率动态响应速度，根据经验，其值可能设计得比较小，导致在频率偏差很大时，无法提供足够的惯量以有效地抑制频率进一步增大。为解决该问题，定义频率偏差界限的概念，其值根据微网最大许可频率偏差Δfmax确定：

式中：fthr为无量纲频率偏差界限，fthr=0.8；fthr_r为真实频率偏差界限，单位Hz，fthr_r=0.4 Hz。

当In1大于fthr，认为频率偏差已经处于较危险范围，此时利用大输出因子K2提高惯量值，整体降低频率变化率与频率波动幅值；而当频率偏差小于fthr，频率偏差仍处于较低范围，此时应用小惯量保证频率响应速度，采用较小的输出因子K1计算自适应惯量值，即

最后，将实时计算得到的惯量Jadp用于微网频率调节过程中，可实现跟踪频率偏差及偏差变化速率的模糊自适应惯量VSG控制算法。

3 仿真与实验验证

为全面验证所提控制方法的有效性，对两个案例分别进行仿真和实验验证。

3.1 案例1

采用Matlab/Simulink2018b搭建案例1的控制系统模型，并与传统的恒输出校正因子（使用K1）模糊自适应惯量VSG控制方法进行对比，其中，主要的系统及控制参数为：额定有功功率PN=10 kV·A，额定无功功率QN=0 kvar，额定电压UN=220 V，额定频率fN=50 Hz，母线电压Udc=800 V，滤波阻抗Zf=0.2 Ω，滤波电容Cf=15µF，虚拟阻尼D=3.5 N·s/m，输入校正因子Kf=2，输入校正因子Kfd=0.001 6，输出校正因子K1=0.6，输出校正因子K2=8.5。

为研究频率变化，负载类型设置为纯阻性负载，额定无功功率为0，频率突变由加减有功功率产生；仿真时长为2 s，系统带额定负载启动，在0.5 s加载120%负载（较小负载突变）造成频率波动，在1 s加载至170%负载（大负载突变），引起大频率波动，在1.5 s恢复至额定负载。

图7为基于传统恒输出校正因子模糊自适应惯量VSG控制的特性曲线。首先，有功功率在负载发生突变后快速响应，启动后稳定时间约为0.05 s，突加大负载时稳定时间约为0.04 s，随后系统有功功率跟踪至设定负载值。此外，虽然在突加负载时功率抖动明显，但是在负载突降时未见明显抖动，同样电压也表现出了相似的特性。由于锁相环的作用，频率响应落后于功率响应，启动后稳定时间约为0.2 s，突加大负载后稳定时间约为0.1 s。图7中，整个控制过程中惯量值比较小，频率响应速度较快，突加负载后超调明显，特别在1.1 s时，频率偏移达到0.51 Hz，超过最大许可频率偏差，系统处于比较危险的状态。

图7 传统模糊自适应惯量VSG控制特性Fig.7 Control performance of traditional fuzzy adaptive inertia VSG

图8为基于改进型模糊自适应惯量VSG控制的特性曲线，与图7相比，有功功率和电压响应过程非常相似，但是频率特性发生明显变化，特别是当频率偏差超过fthr_r以后。具体当突加大负载且频率偏差低于49.6 Hz后，频率变化率迅速减缓，且频率在负载突降前（1.5 s）一直在调整，频率响应速度低，但是突加大负载后最大频率偏移只有0.48 Hz，在安全范围之内，这说明所提出的改进型控制算法在大负载突变时安全性更高。值得注意的是，频率响应速度在频率偏差小于0.4 Hz时与图7类似，具有较好的动态性能。

图8 改进型模糊自适应惯量VSG控制特性Fig.8 Control performance of improved fuzzy adaptive inertia VSG

3.2 案例2

参考文献[20]，搭建一套实验用低压测试平台，平台参数为：额定有功功率PN=100 V·A，额定无功功率QN=0 var，额定电压UN=30 V，额定频率fN=50 Hz，母线电压Udc=100 V，虚拟阻尼D=2.0 N·s/m，输入校正因子Kf=2，输入校正因子Kfd=0.001 6，输出校正因子K1=0.2，输出校正因子K2=5.5。

VSG控制算法在TMS320F2812主控芯片内执行，负载为纯阻性负载，测试数据由数字处理器DSP记录。考虑到所提出的改进型模糊自适应惯量VSG主要在频率偏差较大时发挥关键作用，实验过程设置如下：实验时长为2.0 s，系统带额定负载启动稳定后，在0.5 s直接加载至155%负载（大负载突变），引起大频率偏置，比较传统与改进型模糊自适应惯量VSG的控制性能。

图9为传统模糊自适应惯量VSG控制特性曲线，图10为基于改进型模糊自适应惯量VSG的控制特性曲线。当施加额定负载时，两种控制方法采用同样的输出校正因子产生虚拟惯量值，两系统输出有功功率、电压和频率特性相近，分别可以稳定在100 V·A，30 V和50 Hz，且波动较小。但当突加负载之后，虽然两种控制方法的功率和电压特性仍然相似，但频率响应有明显不同。首先，在传统控制方法中，频率偏差幅值达到0.57 Hz，已经超过最大许可范围，但在改进型模糊自适应惯量VSG算法控制下，频率偏差约为0.5 Hz，尚在最大许可范围之内，这说明提出的改进型VSG控制算法在大负载突变时具有更好的频率抑制效果。其次，当频率偏差比较大时，图9中频率曲线变化速度仍然比较高，而图10中频率变化速率明显降低，这是所提出的基于双输出因子的模糊自适应惯量VSG控制器的重要特点，且该特征是抑制频率偏差的基础。

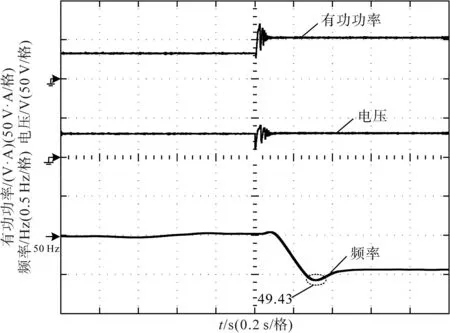
图9 传统模糊自适应惯量VSG控制特性Fig.9 Control performance of traditional fuzzy adaptive inertia VSG

图10 改进型模糊自适应惯量VSG控制特性Fig.10 Control performance of improved fuzzy adaptive inertia VSG

4 结论

提出了一种基于改进型模糊自适应惯量VSG控制的微网频率波动抑制方法，主要研究内容及贡献总结如下：

1）提出了频率偏差界限的概念，并将其融入至模糊控制器的设计过程中。利用频率偏差界限选择模糊控制器输出校正因子，当微网频率偏差超过界限时采用较大校正因子，抑制频率持续波动。

2）设计了模糊自适应惯量控制器，根据频率偏差及频率偏差变化率计算用于实时VSG控制的惯量值，保证系统的动态性能，提高系统安全性。

3）通过仿真和实验验证可得，所提出的改进型模糊自适应惯量VSG控制方法在频率偏差较大时能够抑制频率波动，在频率偏差较小时能够保证系统的动态性能，具有很高的应用价值。