基于先进节块法的六边形三维中子物理程序的开发与验证

陆道纲，吕思宇,*，隋丹婷，郭劲松

(1.华北电力大学 核科学与工程学院，北京 102206；2.非能动核能安全技术北京重点实验室，北京 102206)

三维节块扩散理论作为准确且有效的求解全堆芯耦合扩散方程的方法被核工程领域广泛接受，并应用于轻水堆(LWR)与快堆(FBR)堆芯三维中子通量、功率分布的仿真计算中。由于目前世界上大部分反应堆燃料组件为方形燃料组件，先进的三维节块扩散理论往往是率先应用于笛卡尔坐标系下的中子扩散方程求解。为使这些先进节块扩散理论能应用于具有六边形燃料组件的堆型(如钠冷快堆)中，各科研院所提出了很多方法。Wagner等[1-2]提出的应用于DIF3D程序中的基于横向积分技术的六边形节块展开法，Koyanma等[3-4]提出的通过边界拟合坐标转换法将六边形转变为笛卡尔坐标系的节块展开法，和Chao等[5-7]提出的基于共形映射的六边形节块法等。在前期的工作中，华北电力大学提出了可应用于六边形组件的高阶节块展开法，并基于该方法开发了三维中子物理程序HNHEX[8-9]，该程序以六边形组件为径向计算节点，并根据需要对轴向进行划分，可计算三维中子通量分布，通过基准题对该程序进行了验证并得到了较好的仿真结果。但不可忽视的是，该方法是基于横向积分将六边形节块内部的中子扩散方程通过3个径向方向、1个轴向方向并通过泄漏项耦合的一维中子扩散方程组。这种处理方法会在对面平均通量求二阶导时产生奇异项。六边形高阶节块展开法通过采用Wagner在文献[1]中提出的方法处理奇异项，即通过在一维扩散方程中忽略奇异项，在节点耦合方程中引入补偿项来修复节点平衡关系。相对于笛卡尔坐标系下的节块展开法，这种近似损失了计算精度。而通过共形映射先将六边形各边映射到长方形上，再进行横向积分得到各方向上的横向一维中子扩散方程，则避免了奇异项的产生[5,10]，这种处理方法被证明可显著减小计算误差。

由于高阶节块展开法具有较快的计算速度，且目前反应堆中材料不均匀性主要来自于径向，在轴向不均匀性并不显著。本文通过在轴向上使用高阶节块展开法，并将HNHEX程序中径向上使用的展开法替换为基于共形映射的半解析节块法，通过泄漏项进行耦合开发SA-HNHEX(semi analytic-high order nodal expansion method for hexagonal-z)程序。对VVER-440的二维、三维基准题分别进行建模计算，初步验证该方法与程序的有效性和正确性。

1 求解方法

堆芯以每盒组件为1个径向节点，轴向节点数量可根据需要自行设定，通常为10 cm至25 cm高度。多群扩散方程可写成如下形式：

(1)

(2)

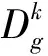
对式(1)的求解需要建立额外的面平均泄漏和节点中子通量之间的关系。将式(1)分别对x-y平面与z方向进行平面积分，可得到通过泄漏项耦合的径向x-y平面与轴向z方向上的中子平衡方程：

w=x,y

(3)

k=1,…,K；g=1,…,G

(4)

由于材料不均匀多产生于径向，所以在径向上扩散方程的求解采用基于共形映射的六边形半解析节块法，轴向上高阶节块展开法已经能够得到较高的计算精度且计算效率相对于半解析方法要高，所以在轴向上沿用高阶节块展开法。

1.1 径向基于共形映射的六边形半解析节块法

在应用于中子物理计算之前，共形映射被应用于静电学和流体力学将等势曲线和场曲线从一种几何图形映射到另一种几何图形上。这种映射方法保留了原来坐标下的角度信息，因此在新的拉普拉斯型微分方程中的拉普拉斯算子与共形映射前保持不变。这正是共形映射在静电学与流体力学中有效应用的原因，类似的，中子扩散方程也是拉普拉斯微分方程，中子流是中子通量的矢量梯度，正如电场是电势的矢量梯度一样。中子通量和中子流之间的正交性在共形映射后也可得到保留。图1为六边形至矩形共形映射示意图[5,10]。图中：JLT为六边形节块径向左侧上表面中子净流；JLB为六边形节块径向左侧下表面中子净流；JRT为六边形节块径向右侧上表面中子净流；JRB为六边形节块径向右侧下表面中子净流。

在图1左侧复平面Z上，二维单群中子扩散方程可表示为：

(5)

如图1所示，复平面Z上的1组正交曲线坐标(x,y)通过共形映射函数w=f(z)变换为复平面W上的1组正交曲线坐标(u,v)，其中w=u+iv、z=x+iy为复变函数。z的实部和虚部与w的实部和虚部分别在复平面Z和W上组成直角坐标系。整个x-y平面上的六边形内部区域被映射到u-v平面上的矩形内部。矩形内部相互垂直的直线U和V是六边形内部的相互垂直的曲线U和V在复平面W上的映射。式(5)中的拉普拉斯算子通过映射得到：

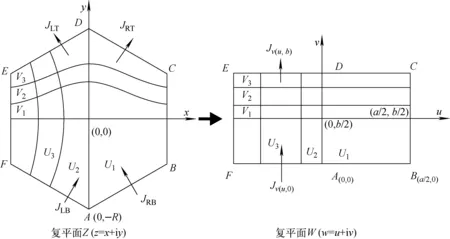
图1 六边形至矩形共形映射示意图

(6)

其中，g(u,v)为共形映射的线型比例函数，其平方为映射区域面积比例函数，映射线型比例函数在映射区域内始终为正，表示由于映射而产生的局部线性比例变化。值得注意的是，保形映射的局部线性尺度变化与方向无关，即映射在所有方向上对局部区域均是各向同性缩放。从式(6)可知，当φ映射到W平面时，其空间梯度将被在所有方向上按1/g因子缩放。可知，共形映射后的中子扩散方程形式如下：

(7)

通过对比式(5)与式(7)可发现，均匀六边形节块被转化为均匀矩形节块后，与裂变截面和吸收截面相乘的非均匀性因子g2是仅与几何相关的映射面积比例函数。映射函数可通过Schwartz-Christoffel方法[11-12]得到，该映射是唯一的，且矩形形状是固定的，具有特定的等高比。如图2设映射后矩形节块的高度为b，底部从-a/2到a/2。图2中：JL为六边形节块径向左侧表面中子净流；JR为六边形节块径向右侧表面中子净流；JT为六边形节块径向上表面中子净流；JB为六边形节块径向下表面中子净流。

图2 节点k内部各方向中子流共形映射关系

将(7)沿v轴方向横向积分，得到一维扩散方程如下：

(8)

与式(3)类似，将式(8)左右两端进行处理，横向积分方程可表示为：

(9)

其中：Σa0为体平均总移出截面；Qu(u)为有效中子源；Lu(u)为横向泄漏项。

(10)

(11)

展开式中的5个展开系数可通过在u=±a/2处的边界条件；横向积分方程(式(9))满足零次矩(W0)、一次矩(W1)、二次矩(W2)权重获得。通过式(10)可得到在u=±a/2处的面平均中子净流和源项、泄漏项的零次矩、一次矩、二次矩。对相邻节块重复同样的展开方式可得到横向一维净流耦合方程的基本形式：

(12)

其中，Cn为群常数确定的耦合系数。将以上方法通过径向扫描原六边形节块可得到3个横向一维净流耦合方程。对于二维径向上总泄漏项Lu的近似需考虑其在径向上其他方向的泄漏与轴向上的泄漏，即：

L(u)=Lxy(u)+Lz(u)

(13)

其中，径向泄漏项Lxy(u)的近似采用阶跃泄漏近似，如图2所示：

(14)

本文轴向泄漏项Lz通过轴向使用的高阶节块展开法得到的轴向表面中子流计算得到。

1.2 轴向高阶节块展开法

轴向上偏中子通量采用高阶节块展开法处理，展开式与基函数如下：

(15)

(16)

(17)

(18)

(19)

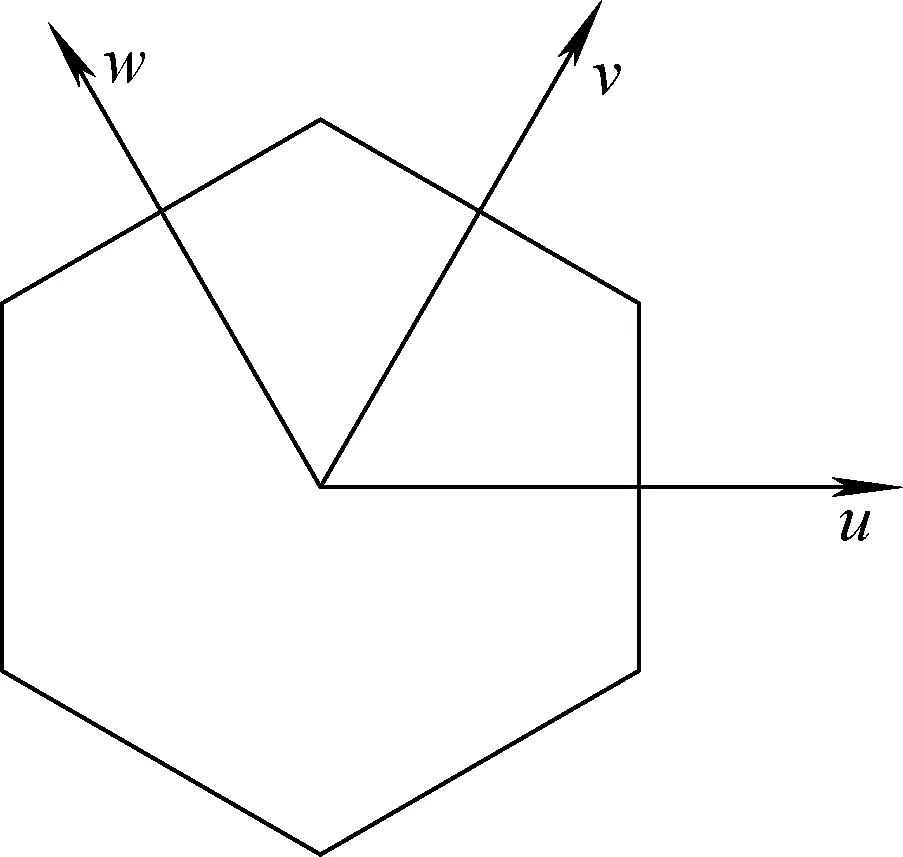
图3 径向扫描方向

1.3 耦合方法

径向的半解析方法与轴向使用的高阶节块展开法通过泄漏项进行耦合，其耦合逻辑如图4所示。图4中：1)轴向求解一维扩散方程得到轴向节块表面中子流；2)径向通过轴向表面中子流计算径向扩散方程中的轴向泄漏项；3)求解径向中子净流耦合的内迭代；4)内迭代收敛后更新轴向一维扩散方程泄漏项中的3个方向上的径向泄漏项；5)重复步骤1～4，直到径向与轴向上中子泄漏耦合收敛后，更新径向、轴向偏通量与相应源项系数完成源迭代[13]。

图4 耦合方法流程图

2 基准题验证结果

通过对原中子物理程序HNHEX求解器的修改并加入了中子泄漏项耦合模块，开发了能用于求解六边形三维中子扩散方程的中子物理程序SA-HNHEX。本文采用VVER-440的二维和三维基准题对该程序进行验证，除基准题参考解外，加入了使用节块展开法的DIF3D-N与使用半解析节块法的ANC-HM计算结果进行对比。

VVER-440基准题是由Seidel等于1984年提出的[6]，其堆芯直径上有25盒组件，组件对边距为14.7 cm。反射层组件外部边界条件考虑为真空。整个堆芯有7盒控制棒组件，当控制棒组件插入堆芯时，会将下部的燃料组件从堆芯下部推出，从而带来更大的负反应性反馈，在二维基准题中，控制棒组件为全部插入堆芯，在三维基准题中为插入1/2。表1列出VVER-440基准题所使用的群常数，图5为二维VVER-440基准题中1/12堆芯布置情况及SA-HNHEX计算结果相对于参考值(DIF3D-FD采用600和864三角形/六边形网格推测得到[6])的相对偏差。

图5 VVER-440二维基准题堆芯布置及真空边界条件计算结果

表1 VVER-440 基准题材料群常数

表2列出VVER-440二维基准题计算结果对比。如表2所列，SA-HNHEX计算VVER-440二维基准题本征值keff为1.016 01，与基准参考值误差为63 pcm，与同样使用共形映射解析节块方法的ANC-H相比，精度相当。与使用高阶节块展开法的HNHEX相比，在节点功率最大误差与本征值误差上计算精度均有明显提高，但在计算时间上有所增加。

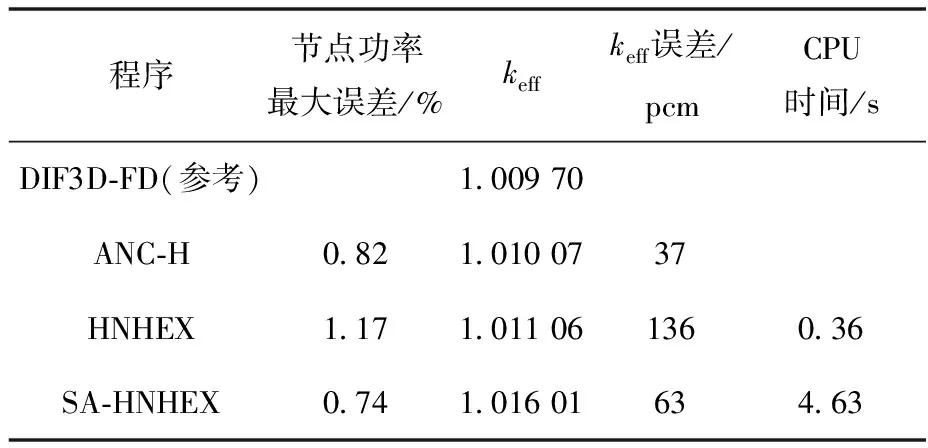
表2 VVER-440二维基准题计算结果对比

VVER-440三维基准题使用的群常数及堆芯径向布置方案均与二维基准题相同，轴向上控制棒组件为半插入堆芯，如图6所示。堆芯高度为250 cm，堆芯上下均增加了25 cm反射层，轴向、径向上的边界条件均考虑为真空条件。

图6 VVER-440三维基准题控制棒轴向位置

表3列出VVER-440三维基准题计算结果对比。如表3所列，SA-HNHEX与HNHEX均采用了两组轴向节点数(12节点与24节点)对VVER-440三维基准题进行计算。由于SA-HNHEX在径向上采用了更精确的半解析节块法，其计算精度有显著提升，在12个轴向计算节点的情况下已达到HNHEX使用24轴向计算节点的精度。在计算耗时上，由于SA-HNHEX在轴向上使用更快的高阶节块展开法，相较于ANC-H在保证计算精度相当的情况下有更好的计算速度表现；相较于HNHEX轴向24个计算节点，其计算耗时的小幅增加所带来的精度上的显著提高也体现了该方法较高的性价比。

表3 VVER-440三维基准题计算结果对比

3 结论与展望

本文基于先进节块方法提出了一种综合径向共形映射半解析-轴向高阶节块展开法的三维六边形中子扩散方程求解方法，通过对原六边形高阶节块展开法求解器HNHEX的修改开发了SA-HNHEX三维六边形中子扩散方程求解程序，通过使用VVER-440型反应堆的二维、三维基准题对该方法及程序进行了初步验证。计算结果与参考值符合较好，在计算精度上与同类程序相当，并在计算精度上相比原程序HNHEX有显著提升，且在计算耗时的增加上较为友好。

在未来的工作中，将对SA-HNHEX的迭代进行加速优化，并将该求解器与快堆系统分析程序SAC[14-16]进行耦合开发与验证。