基于格子Boltzmann方法的反应堆核-热-流耦合模拟
王亚辉,马 宇
(中山大学 中法核工程与技术学院,广东 珠海 519082)
核反应堆堆芯是一个典型的多物理耦合系统,其中的核-热-流耦合过程是反应堆工程模拟中的一个主要研究点[1-2],尤其是对于反应堆设计及安全分析。中子输运过程决定了核燃料中中子裂变产生的能量,而热工水力过程决定了温度分布,并通过多普勒效应影响宏观中子截面。由于这一特点,核反应堆行为的可靠分析需要涉及中子输运和热工水力过程的多物理耦合[3-4]。从数学角度来看,这些多物理模拟的实现依赖于在不同物理场之间有效传输数据的能力。因此,在相同方法下解决耦合问题,可有效消除外部数据交换和插值。然而,由于不同物理场控制方程之间的差异性以及中子输运方程的复杂性,对其耦合求解存在一定的难度。当前的研究工作普遍基于不同数值方法对不同物理场进行求解,随后在不同物理场之间增加外部数据接口和插值过程,这使得多物理耦合实现困难,并且可能会降低精度[5]。
格子Boltzmann方法(LBM)[6-9]是一种起源于流体动力学求解的数值方法,该方法采用介观分布函数来求解宏观变量的演化过程,可将不同的控制方程转换为相似的线性LBM方程,采用相似的格式进行求解,这使得LBM在多物理耦合模拟中具有突出优势。相比于传统数值方法而言,LBM具有极为简单的形式,只需上百行程序即可实现复杂物理过程的模拟;同时由于LBM方程只与当前的节点以及上游的一个节点有关,该方法具有极强的并行特性。基于以上优势,LBM在流动传热[10-13]、多相流[14-15]、流固耦合[16]、多孔介质流[17-19]、磁流体[20-21]、化学反应[22]、堆芯物理[5,23-26]等方面受到了大量的关注。
本文建立求解反应堆堆芯核-热-流耦合过程的LBM模型,将核-热-流不同物理过程统一到相似的LBM格式下采用相似的数据结构和离散格式进行求解,消除不同物理场之间的外部数据传输和插值过程,降低多物理耦合求解的实现难度。
1 基于LBM的核-热-流耦合模拟
反应堆堆芯内部存在着多种物理过程的相互耦合,工程中常常考虑核-热-流耦合过程。对于燃料区域,温度分布通过改变中子截面进而影响中子物理过程,同时裂变产热又作为热源影响传热过程。对于慢化剂区域,除以上效应外,温度分布还受到流动过程的影响。总体而言,核-热-流耦合过程可以采用如下控制方程组进行描述,包括中子输运方程、缓发中子先驱核守恒方程、大涡模拟(LES)方程以及能量守恒方程:
(1)
(2)
(3)
(4)
(5)
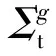
(6)
其中,Ef为1次裂变释放的能量。式(2)左侧第1项(对流项)主要存在于液体燃料堆芯中(如熔盐堆),是缓发中子随液体燃料流动迁移而产生的。在核-热-流耦合计算中,中子宏观截面Σx与温度T相关,即Σx=Σx(T)。
为实现堆芯核-热-流耦合过程的高效准确模拟,本文采用了具有多物理耦合特性的LBM进行求解,该方法能将不同的物理过程转化为相似的LBM形式并在相似的数据结构以及离散格式下采用相似的求解格式实现耦合求解。对堆芯核-热-流耦合过程,采用如下LBM模型:
(7)
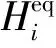
二维条件下典型的离散速度模型有D2Q4(2维4速)和D2Q9(2维9速)模型,如图1所示。
a——D2Q4;b——D2Q9
D2Q4离散速度定义为:
(8)
D2Q9离散速度定义为:
e=
(9)
其中,c为格子迁移速度,c=δx/δt,δx为格子宽度,即网格尺寸。
该模型的平衡态分布函数和无量纲弛豫时间可表示为:
(10)
(11)
其中:A、B、C为物理场参数;ϖ为LBM格子方向权重;Ψ为广义宏观变量;ζ和U分别为广义扩散系数及广义宏观速度;I为单位对角矩阵;τf为为广义无量纲弛豫时间;cs为LBM格子声速。
在统一LBM框架下,所有物理场可采用相似的过程进行演化计算,包括碰撞和迁移过程如下:
(12)
(13)
其中,H*为碰撞后分布函数。宏观变量可通过对所有格子方向的分布函数求格子速度的0阶矩得到:
(14)
通过对方程中的变量赋予不同的定义,以上的统一LBM模型可被用来求解不同的问题。本研究中,对中子输运问题的模拟按照精度需求的不同可选择中子输运SN方程LBM模型、SP3方程LBM模型以及扩散方程LBM模型。为了使该核-热-流耦合LBM模型能用于固体燃料反应堆及液体燃料反应堆,本研究中对考虑流动效应的缓发中子先驱核守恒方程采用有限Boltzmann形式的LBM模型。
基于中子扩散方程和中子输运SP3方程的特性,二者求解的LBM模型均采用D2Q4格子速度模型。由于缓发中子方程和SN方程均具有强对流特性,这两个LBM模型均采用D2Q9格子速度模型。流动速度场的LBM模型也采用D2Q9格子速度进行模拟。对于传热方程LBM模型,可以与LES方程的LBM模型类似地采用D2Q9格子速度模型,但对于不考虑流动效应的中子输运-传热耦合过程,传热方程LBM模型可采用更高效且稳定的D2Q4格子速度模型进行模拟。
本文给出核-热-流耦合过程中几种典型的边界条件处理方式,包括中子输运过程的真空边界、反射边界、流动传热过程中的对称边界、绝热边界、无滑移边界、自由出流边界等。从LBM的边界处理角度来说,这些边界可统一用两种方式处理,包括反弹(BB)边界及非平衡外推边界。
1)反弹边界
反弹边界的定义是在边界上出射的分布函数经过边界反弹后,沿其镜像对称方向再次反弹回计算域中,这种边界一般被用于反射边界、对称边界及绝热边界。以右边界为例,此时对称边界的定义如下:
H3(B)=H1(B) D2Q4
H3,6,7(B)=H1,5,8(B) D2Q9
(15)
其中,B为边界节点。
2)非平衡外推边界
非平衡外推边界基于这样一个假设:节点上的分布函数Fi可表示为平衡态部分和非平衡态部分的和:
(16)
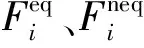
在非平衡外推边界中,边界节点的平衡态分布函数可由式(10)直接给出,而假设边界节点的非平衡部分可由其内一层节点的非平衡态部分外推得到:
(17)
其中,O为边界向内一层节点。
由于非平衡外推边界采用外推方式,理论上该方法可适用于所有类型的边界条件处理,包括前文中的反射边界、对称边界及绝热边界等。
2 数值实验
选取典型问题对本文建立的核-热-流耦合LBM模型进行测试与验证。在流场计算中,Smagorinsky系数设为Cs=0.1;所有模拟的误差限均取为10-6。由于中子输运LBM模型(包括SN方程、SP3方程以及扩散方程)及核-热耦合LBM模型均已在文献[27]中进行过验证,本文不再重复,只着重对基于LES方程的流场流动LBM进行验证。
2.1 LBM模型验证
为验证核-热-流耦合LBM在不同流态流场模拟的准确性,对典型的方腔驱动流进行了模拟研究[28-30]。为研究耦合LBM模型对不同Re的适应性,分别对Re=100、1 000以及10 000的流场进行了模拟。当Re=100和1 000时,分别采用128×128网格,当Re=10 000时,由于湍流流态的复杂性,采用256×256网格进行模拟,格子速度模型统一采用D2Q9模型。方腔的高和宽分别取为H和L,流体驱动速度为U0。
沿水平中线的横向相对速度分量以及沿垂直中线的纵向相对速度分量如图2所示,并与直接数值模拟(DNS)方法进行对比。由图2可看出,本文核-热-流耦合LBM的模拟结果在不同Re下与参考解均吻合得很好,证明当前的耦合LBM模型对层流和湍流条件均有较强的适应性及较高的精度。

a——水平中线横向相对速度分量u/U0;b——垂直中线纵向相对速度分量v/U0
2.2 基于LBM模型的简化熔盐堆核-热-流耦合分析
液体燃料熔盐堆(MSR)是第4代反应堆中唯一一种液体燃料堆芯,该堆芯能在高温条件下保持较低的蒸汽压,具有较高的安全性,同时可实现小型化应用。不同于固体燃料堆芯,MSR的核燃料溶解在熔盐慢化剂中,随着熔融盐在堆芯中流动而迁移,熔融盐的流动效应对缓发中子先驱核的迁移行为产生影响,同时缓发中子先驱核的迁移影响中子注量率和温度分布,而温度分布又通过中子截面和材料热物性影响中子输运和流动过程。因此,对于MSR而言,中子输运-传热-流动过程是强烈耦合在一起的,必须对其进行耦合研究。
为研究耦合LBM模型对MSR模拟的适应性及MSR内部的多物理耦合行为,基于本文建立的耦合LBM模型对简化MSR内部的核-热-流耦合过程进行模拟分析。基于相关文献[31]建立了正方形简化MSR模型,其内部熔盐流动被作为自由流动处理。反应堆核-热耦合过程的准确性已在之前的研究中进行了充分验证,同时本文建立的LBM模型对于流动复杂过程模拟的准确性也已进行了验证,为此本文不再进行重复验证。简化堆芯结构为2 m×2 m的方形区域,其内部存在自由流动的液体熔盐,核燃料被溶解在液体熔盐中,随液体熔盐流动而流动。该问题考虑双群6组缓发中子,模拟过程中考虑中子物性及材料热物性的温度反馈。
对该问题考虑中子输运-传热-流动耦合过程模拟,不考虑熔融盐压缩效应,并且使用Boussinesq方程近似熔盐流动过程中的浮升力随温度的变化。该堆芯是一个均匀液体反应堆,四周边界均为真空无入射中子边界,缓发中子先驱核在壁面处均被反射回堆芯,没有泄漏。熔盐在壁面处的流动边界均为无滑移边界,同时左右壁面及下壁面均为静止壁面,上壁面以Ud的速度驱动堆芯内熔盐流动。堆芯内热量不通过壁面传递出堆芯,即四壁面均为绝热边界。熔盐堆芯热量导出通过堆芯内的散热器实现,散热器散热过程近似可表示为:
q‴=γ(Tref-T)
(18)
其中:Tref为参考温度,Tref=900 K;γ为均匀体积换热系数,γ=106W/(m3·K);q‴为散热器换热功率密度。
分析了不同条件下的堆芯内耦合行为,分析条件分别为:中子截面无温度反馈(Ud=0.5 m/s)、中子截面有温度反馈(Ud=0.5 m/s,5 m/s)。图3示出不同条件下瞬发中子注量率φ1、缓发中子先驱核C1以及功率P的分布,图4示出堆芯流线图。图3中flagT=0表示无温度反馈,flagT=1表示有温度反馈。由图3可看出,温度反馈强烈地影响中子注量率分布和功率分布,同时对于缓发中子也有较为明显的影响。
当不考虑温度反馈条件时,由于堆芯内部中子截面分布均匀,此时中子注量率分布从堆芯中心向堆芯边缘逐渐降低,中子注量率最大的区域集中在中心区域附近,因此此时堆芯功率的最大值也集中在堆芯中部,如图3a、c实线所示。由于低速下熔盐内部浮升力起主要作用,缓发中子将随着熔盐向堆芯上部迁移,缓发中子密度在堆芯上部较大,如图3b实线所示。
如图3中虚线所示,当考虑温度反馈时,堆芯中心处中子注量率更大更加集中,同时中子注量率分布和功率分布集中在堆芯偏下区域。这一现象是由缓发中子先驱核和温度分布共同直接作用影响的。一方面,由温度反馈引起的宏观截面的变化直接影响了中子输运过程,间接导致堆芯下部中子注量率分布集中。当Ud=0.5 m/s时,浮升力和对流传热同时起作用。在相对较强的浮升力作用下,由于密度降低,温度较高的燃料随熔盐材料向上流动,如图4a所示。因此,高温流体集中在堆芯上部,使得上部区域中的宏观截面小于下部区域的宏观截面。由于燃料在下部区域具有更强的慢化和裂变效应,因此中子分布更集中在该区域,同时相应地功率分布也更集中于该区域。中子在下部的积聚导致了缓发中子的积聚,同时由于燃料与熔融盐一起流动,所以对流效应使得缓发中子先驱核向堆芯的下部蓄积,这增加了堆芯下部的缓发中子源,也相应地增加了瞬发中子在下部的积聚。

图3 不同条件下快群中子(a)、缓发中子先驱核(b)及功率(c)分布对比
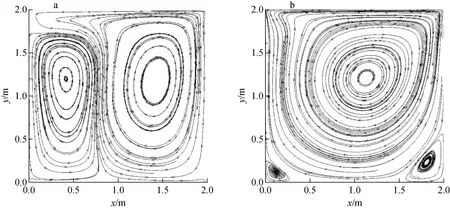
图4 低速(a)和高速(b)条件下堆芯流线图
图3中点划线展示了流速对于MSR堆芯工况的影响,即对流传热强度的影响。相较于虚线情况而言,点划线所带有的条件具有较高的驱动速度,并因此具有较高的对流传热效果。在研究温度和流动条件时,可发现当Ud=5 m/s时浮升力对流体流动的影响相对较小,此时流体呈现强迫对流状态,如图4b所示。在这种情况下,由于浮升力导致的左侧涡结构变小,而由于驱动力导致的右侧涡结构主导了流场。在这种条件下,不同温度的流体通过流体流动相互混合变得均匀,并且由浮升力引起的高温流体的上浮过程被减弱。主流区域中相对均匀的温度分布导致该区域中子截面更均匀。因此,中子分布更集中在堆芯的中心区域,堆芯功率也集中在靠近中心区域。
3 结论
本文针对反应堆堆芯内中子输运-传热-流动多物理耦合过程,构建了核-热-流耦合过程的多物理场耦合LBM模型,其中中子输运过程涵盖了SN方程、SP3方程以及扩散方程3种不同近似;缓发中子先驱核守恒方程考虑了MSR堆芯中燃料流动效应,使得该模型对于不同尺度、不同特点的堆芯均具有较强的适应性。基于LBM的实现简单性以及多物理耦合特性,降低了多物理耦合模拟的难度,同时消除了传统外耦合方法的数据传输与插值过程。数值验证结果表明,本文建立的耦合LBM模型对不同流态的流动过程均具有较强的适应性与较高的精度。基于耦合LBM模型对MSR内部核-热-流耦合行为的研究表明,温度反馈对于高温堆芯有较为明显的作用,不可忽略;同时提高液体熔盐流速能够有效展平功率和温度分布,改善传热。耦合过程的模拟结果表明本文的LBM模型对核-热-流耦合过程具有良好的适应性,同时能够对液态燃料堆芯条件给出合理的研究结果。
本文研究是LBM在堆芯多物理耦合模拟领域的一个初步尝试,在将来的工作中,将进一步扩展所建立的耦合LBM模型,包括多相流动过程、耦合燃耗过程、力学过程等,进一步提高模型适用性以及物理场耦合的全面性。

