订单可拆开加工的两代理分批调度问题 ①

刘甲玉， 耿志超

1.河南交通职业技术学院 公共基础教学部， 郑州 450001； 2.郑州大学 数学与统计学院， 郑州 450001

现代生产企业为提高生产效率普遍采用分批加工模式， 即在多个车间或机器上同时加工一定数量的产品或零部件． 比如， 在半导体加工厂里集成电路板耐热测试的熔断工序[1]中， 测试容器可以同时处理大量的电路板． 关于分批调度的研究已有大量结果[2-3]． 本文关注如下的实际生产情形： 某加工厂接到了来自两个客户的多个订单， 每个订单对应于不同类型的产品或同一类型产品的不同款式， 每个订单中的产品数量不同； 两个客户对其订单有不同的期望和要求， 其中一个客户期望为其各个订单支付的加工费用均衡化(本文用最小化最大加工费用表示)， 而另一客户期望其各个订单均尽早交付(本文用最小化完工时间之和表示)． 每个订单均可分拆成多个部分并连续地在相邻的批中加工．

文献[4-6]研究了订单可拆分加工的分批调度问题， 但均是针对单个代理情形， 而本文将在两个竞争代理的背景下研究相关问题．

多代理排序问题最早是由文献[7-8]提出的． 针对两个代理的多个不同的目标函数组合， 文献[7]研究了两个代理的目标函数的加权和问题， 设计了多项式时间算法并证明了NP难性； 而文献[8]研究了限制问题， 即在满足不超过一个代理目标函数的门槛值的条件下， 使另一个代理的目标函数最小化， 同时也研究了几个Pareto 优化问题， 设计的算法能够在多项式时间内枚举所有Pareto 最优点， 并为每个Pareto最优点找到一个对应的Pareto最优解． 文献[9]中将多代理模型分类为： 竞争代理模型(CO)、 非不交代理模型(ND)、 Interfering代理模型(IN)、 多指标代理模型(MU)， 并对多代理排序问题的研究结果进行了详细的综述． 文献[10]研究了单机、 工件有到达时间并允许中断且具有多个瓶颈指标的情形下的相关多代理排序问题， 给出了多项式时间算法或证明了NP难性． 该论文在求解多指标折中排序的方法上有巨大创新． 文献[11-12]研究了在满足其中一个代理的最大费用不超过给定常数的条件下最小化另一个代理的总误工量的排序问题， 给出了拟多项式时间算法． 文献[13] 研究了最小化总的加权误工量的多代理折衷指标排序问题， 证明了当代理的个数是变量时问题是强NP难的， 当代理的个数是固定值时问题是NP难的， 并设计了拟多项式时间算法和完全多项式时间近似方案． 更多相关工作可参见文献[14-16]．

1 问题描述

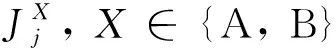
(1)

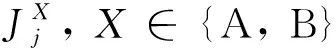
(2)

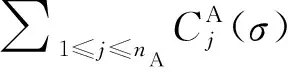
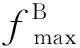
2 算法设计与分析

2.1 NP难性

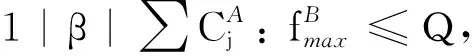
1) ESP问题． 给定2m+1个正整数a1，a2，…，a2m和C， 满足∑1≤j≤2maj=2C， 问是否存在指标集{1， 2， …， 2m}的一个划分(I1，I2)， 使得∑j∈I1aj=∑j∈I2aj=C且|I1|=|I2|？

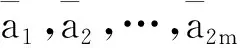
引理1RESP是NP完全问题．

(3)

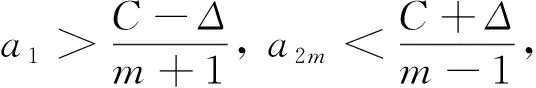
进而， 因a1≤a2≤…≤a2m， 故对任意1≤j≤2m， 有

又由于

因此， 上面构造的实例确实是问题RESP的一个实例．

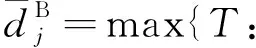
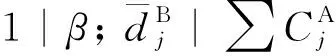
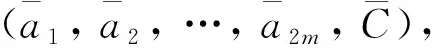
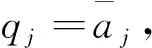
因此，σ是排序实例满足要求的可行排序．

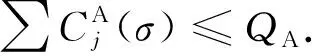
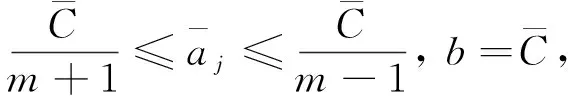
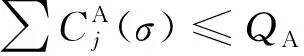
情形2J2m+1被拆分成两部分， 其中一部分在第一批ψ1， 另一部分在第二批ψ2． 由于来自不同代理的工件不能在同一批中加工， 故其他工件将填满第三批ψ3和第四批ψ4， 可能会有某个工件被拆分成两部分， 其中一部分在ψ3， 另一部分在ψ4． 类似情形1中结尾部分的证明， 可得

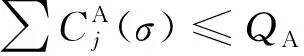
由引理2可直接得到下面的定理．

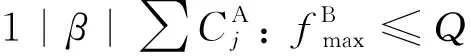
2.2 动态规划算法

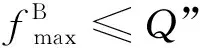
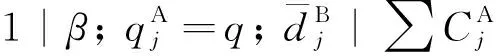
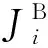
由上述分析可知， 在新排序σ′中， 代理B的所有工件仍然满足截止日期的要求， 代理A的工件的完工时间之和没有增加． 因此，σ′也是问题的一个最优排序． 接着， 如果σ′仍然不具有引理中描述的最优解的结构， 则重复上面的移动操作． 经过有限次重复操作后， 将会得到一个满足条件的最优解．

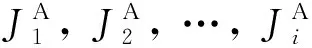
4) 递归关系：

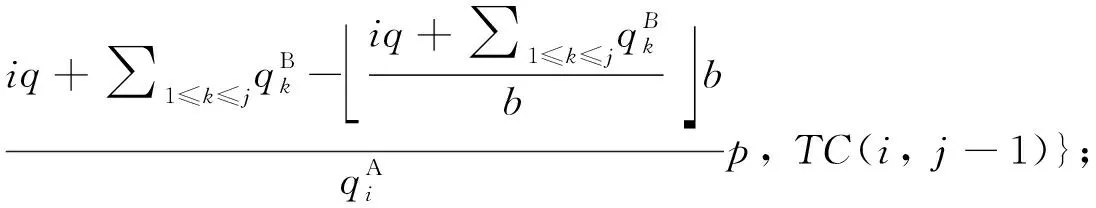
5) 最优值为TC(nA，nB)， 最优解可通过反向追踪找到．

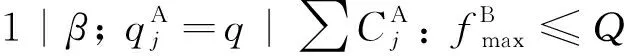
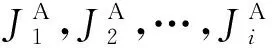
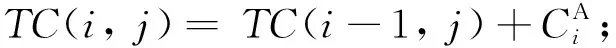
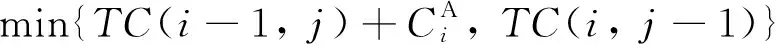
接下来， 分析算法的运行时间． 在DP算法中， 步骤1)对于给定的门槛值Q， 计算代理B的每个工件的截止交货期， 需要采用二元搜索方法花费O(logQ)时间完成， 于是， 计算代理B的所有工件的截止交货期共需花费O(nBlogQ)时间； 步骤2)对代理B的工件按截止交货期由小到大重新标号需要花费O(nBlognB)时间； 步骤3)-5)是动态规划的迭代执行过程， 至多需进行nAnB次迭代， 每次迭代可以在常数时间完成， 于是， 总共花费O(nAnB)时间． 综合上面的分析， DP算法的运行时间为

O(nAnB)+O(nBlogQ)+O(nBlognB)=O(nAnB+nBmax{lognB， logQ})

3 结论

本文研究了工件可拆分的多代理分批调度问题， 目标函数是在满足不超过一个代理的最大加工费用预算条件下， 最小化另一个代理的工件的完工时间之和． 证明了此问题是NP难的， 并对该问题的一个特殊情形给出了多项式时间算法． 未来， 可进一步研究其他目标函数， 如加权完工时间等问题．