基于小波分析的水质变化及预测研究
——以涡河为例
赵贵章,王淑丽,李志萍*,龚建师,王赫生
(1.华北水利水电大学地球科学与工程学院,河南 郑州 450011;2.中国地质调查局南京地质调查中心,江苏 南京 210016)
由于水环境系统具有高度复杂性,且水质指标数据具有不确定性、非线性等特征,因此不断进行水质变化规律分析和预测方法改进是必要的[1]。涡河作为淮河流域第二大支流,水质的变化严重影响着淮河水质及沿岸地区国民经济的进一步发展。通过分析涡河流域长期水质监测数据,掌握流域水质的时间格局特征,进而对水质进行有效预测,对深入了解涡河水资源循环规律,保护涡河流域生态环境至关重要。
小波分析具有时频局部化特征,它可以揭示水文序列的周期变化特征和多尺度变化规律[2],BP神经网络能大规模学习和存储输入输出模式的映射关系,且能够较好处理非线性系统,符合水质预测的要求[3]。因此,采用小波多分辨分析能力和神经网络的自学习能力特性相结合的方式,可以更好地探究水质变化规律。国内外学者也将小波分析应用于水质时间序列分析的研究中。一部分学者通过小波分析对水质序列原始数据进行降噪处理,剔除干扰数据,发现能够提高预测结果的准确度;另一部分学者研究了小波分析在水质变化规律中的应用,探讨了水质指标时间序列的周期模式以及时间格局特征[4-6];还有一部分学者将小波分析与神经网络相结合对水质指标进行预测,发现该种组合模式预测精度更高[7-8]。
小波分析具有多分辨分析的特点,可以对信号进行不同尺度上的分解,通过小波分解得到的小波系数、小波方差等信息,可以用于识别各水质指标时间序列的周期变化规律及突变点,该方法对水质时间特征的演化研究更精细。神经网络与小波分析相结合是国际上研究的热点之一。小波神经网络既有神经网络的自学习能力特性,又有小波的局部特性,弥补了以往神经网络预测时不分主次的不足,提高了网络的稳定性。本研究以涡河流域水质指标为研究对象,以期为小波分析在水质序列变化规律及预测方面的应用提供参考。
1 研究区概况
涡河是淮河第二大支流,也是淮北平原区主要河道,起源于河南省开封市贾鲁河,流经开封、通许、扶沟、太康、鹿邑和安徽省亳州等地,最终注入淮河,具体位置见图1[9]。涡河流域地势平坦,河道坡降较小,受季风气候影响,区域年降水量分配不均,主要集中在6—8月,多年平均年降水量765 mm,多年平均径流量1.5亿m3。20世纪以来,随着工农业生产的快速发展,污水大量排入河流,导致涡河入境水质不佳,涡河水体受到严重污染。进入21世纪,伴随着河长制的推行,以及涡河生态建设示范带的推进,涡河的流域水质明显好转,目前主要是Ⅱ、Ⅲ类水。

图1 涡河流域位置
2 研究方法
2.1 小波分析
小波分析可以对时间和频率进行局部化分析,最终实现高频的时间细分和低频的频率细分。它是继傅里叶变换以来科学方法的重大突破。在实际场景中,有效信号频率较低且相对稳定,而噪声频率一般较高。小波变换就是找到一组低通和高通滤波器组,对原始信号进行连续向下分解,得到一系列具有不同分辨率的低频概貌信号caN和高频细节信号cd1,…,cdN,从而大大增强了局部信号。对这些低频和高频信号进行重构,得到去噪后的信号,提高了模型的抗噪性。
小波是一种特殊的波形,通常用小波母函数ψ(τ)来表示,对ψ(τ) 进行一定的时间上的平移和尺度上的伸缩,就可以得到小波函数基:
(1)
(2)
式中b——平移因子;a——尺度因子。
小波变换的含义是尺度参数a和平移参数b的函数,是一个时间-尺度分析。连续小波变换公式:
(3)

由于连续小波变换的过程会产生许多冗余数据,在实际使用中连续小波必须加以离散化。因此将尺度参数a和平移参数b离散化后得到离散小波变换。通常情况下,离散化公式分别取作:
(4)
式中,a0>0,j∈Z。对应的离散小波基可表示为:
(5)
离散小波变换公式:
(6)

最后,将所有低频信号和高频信号相加实现重构,还原公式如下:
(7)
式中S(t)——还原之后的数据;ψj,k(t)——低通滤波器;h(ψj,k(t))——高通滤波器。
本研究采用常用的Morlet小波,通过小波分解,得到小波系数、小波方差等信息,识别涡河流域2005—2018年的水质指标多时间尺度变化特征及其突变特征。Daubechies(dbN)正交小波基,由于其良好的时频分析性能,已在众多领域应用[10]。基于Daubechies(dbN)小波,对主要影响指标进行小波多分辨率分析,为小波神经网络预测模型的建立进行预处理[7,11-13]。
2.2 BP神经网络
BP神经网络能够较好处理模糊的非线性关系,因而可以很好适用于水质预测等复杂问题的研究[14]。本研究进一步探讨,基于小波分析的BP神经网络模型在水质预测方面的适用性。所采用的是反向传播人工神经网络BPNN(Back-Propagation Artificial Neural Network),其典型结构为3层网络模型,即输入层-隐含层-输出层,具体原理见图2。
输入层、隐含层与输出层之间的神经元连接可描述为:
a1=f(IW·Pi+b1)
(8)
a2=f(LW·Pi+b2)
(9)
式中a1、a2——隐含层和输出层的计算值;Pi——输入量;IW、LW——隐含层连接输入层和输出层之间的权重;b1、b2——隐含层与输入层和输出层之间的偏差值。
其中,隐含层的传递函数采用双曲正切S型函数:
(10)
输出层的传递函数为纯线性函数:
f(x)=x
(11)
2.3 技术方法
本文通过小波分析对涡河流域水质指标进行多尺度变化规律分析,并结合BPNN神经网络对其进行预测。首先,使用主成分分析方法确定关键水质参数,这作为水质预测的目标值,提高预测效率。再通过相关性分析方法将与目标参数相关性较强的水质参数筛选出来并作为预测目标值的输入值,提高预测精度。最后通过Morlet小波分析涡河流域水质指标多尺度变化规律,为水质预测周期提供参考。
在模拟实测水质数据时,需要预处理工具去噪来提高模型的精度,而小波分解能将原始数据中不同频段的信息进行分解,极大地降低数据复杂度,再分别对这些数据进行预测从而提高预测精度。因此,通过比较几个Daubechies小波,选用最为合适的小波基和分解尺度对目标参数的时间序列数据进行降噪处理,得到低频概貌分量(caN)和多个高频细节分量(cdN)。
通过BPNN神经网络,分别对多个分量进行预测,并将其预测结果相加即为目标值的最终预测结果,BPNN模型均采用3层网络结构,主要采用自动完成的“试错法”来训练模型并获取最佳的模拟效果,可调整的主要参数包括隐含层神经元数目、迭代次数、动量因子和学习速率等。具体的技术路线见图3。

图3 技术路线
3 数据处理及分析
3.1 数据来源
本研究数据来源于涡河流域中下游的4个监测断面2005—2018年(共168个月)的水质指标每月一次监测值,其中玄武闸断面位于河南省鹿邑县,大寺闸断面、涡阳闸断面和蒙城闸断面位于安徽省内,具体断面位置见图1。应用的水质指标为溶解氧(DO)、高锰酸盐指数(KMnO4)、氨氮(NH4-N)、化学需氧量(COD)和总磷(TP)共5项,其监测数据完整且连续。
3.2 主成分分析
为提高预测效率,对溶解氧、高锰酸盐指数、氨氮、化学需氧量和总磷5个水质指标进行主成分分析选取预测参数。具体主成分分析结果见表1。由表1可知,第一主成分方差贡献率为47.56%,其反映了原变量的大部分信息,其中化学需氧量、氨氮和高锰酸盐指数得分较高,且化学需氧量得分最高;第一和第二主成分方差累计贡献率为 69.71%,其中溶解氧得分最高为0.81;第三主成分中,总磷得分最高达到了1.07。

表1 主成分分析结果
目前影响涡河流域水质的主要因子为以化学需氧量为代表的,包括氨氮、高锰酸盐指数在内的第一主成分因子。它反映出的信息一方面为有机物指标,如化学需氧量和高锰酸盐指数,另一方面为水体营养盐的指标,如氨氮。说明目前导致涡河流域污染的主要原因为有机污染,因此利用主要污染因子,即用化学需氧量的变化来反映涡河流域污染的变化是可行的。通过分析化学需氧量与各指标间的相关性,为化学需氧量的预测选择合适的输入参数,具体相关性分析结果见表2。由表2可知,化学需氧量与高锰酸盐指数、氨氮的相关性较强,相关系数分别达到0.604、0.650,因此将其作为化学需氧量预测模型的输入变量。

表2 各指标相关关系
3.3 小波分析
基于主成分分析法选取了涡河流域水质的主要影响因子,即化学需氧量。通过对比分析选择合适的分解尺度对化学需氧量原序列进行分解,具体对比结果见图4。
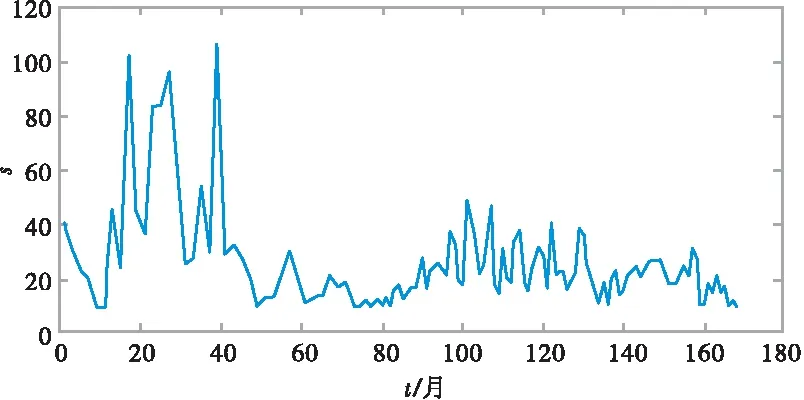
a)小波基(s)
由图4a—4e可以看出,随着分解尺度N的增加,曲线变得更平滑,并趋近原序列,但同时会丢失许多细节成分,当N=5时,曲线太过平滑,无法反映原始序列的峰值。综合比较表明,db2既能显示化学需氧量原序列s的大致概貌,细节成分保留也较完整,而且能很好地反映峰值。由于国内外缺乏最佳小波基的规范性选取方法,但不同小波基的预测结果差别不大,因此,综合比较选择db2小波基对化学需氧量序列进行小波分解。
由图4f—4i可以看出,低频概貌部分体现了原始信号的基本形状,可以看成是原始序列的一个近似。随着分解尺度N的增大,分解序列变得越来越光滑,然而当N=3时,曲线太光滑,无法表现原序列的总体概貌。综合比较当N取2时,最适合于化学需氧量时间序列的小波分析。此时化学需氧量原序列s分解如下:
s=ca2+cd2+cd1
(12)
式中 ca2——趋势成分;cd2——周期成分;cd1——随趋成分。
3.4 神经网络分析
构建化学需氧量小波BPNN模型时,其中ca2分量为原序列的趋势项,应考虑与化学需氧量变化有关的相关变量,因此选取与主要影响因子相关系数较大的指标,即高锰酸盐指数和氨氮作为预测ca2的输入变量,ca2为输出变量;cd2为原序列的周期项,cd1为原序列的随趋成分,与各水质参数相关性不大,基本只与原始序列自身的变化有关,因此选择化学需氧量本身作为其输入,cd2和cd1分别作为输出,然后将所有分变量预测结果叠加作为化学需氧量最终预测结果。经过多次试验测试与参数调整,在保证网络快速收敛的同时又具有较高的预测精度,使模型达到最优结果。训练拟合中db2-2相关参数的最终配置结果见表3。

表3 模型关键参数
4 结果与讨论
4.1 水质指标周期变化规律分析
基于Morlet小波,对涡河流域河流2005—2018年,共168个月的溶解氧、高锰酸盐指数、化学需氧量、氨氮和总磷进行多尺度变化分析。通过小波实部等值线图和小波方差来识别不同水质指标的主周期及变化特征,具体结果见图5。

a)溶解氧等值线

e)化学需氧量等值线
由图5小波系数等值线可以看出,不同水质指标序列存在以不同尺度随时间交替变化的特性,图5小波方差可看出,各指标的小波方差图的主要峰值所对应的时间尺度与小波实部等值线图所显示的波动变化规律相吻合。从图4可知:涡河流域溶解氧8、18、33、64个月尺度交替变化表现较清晰,波动极值点分布规律明显,以18个月尺度较为显著,说明涡河流域溶解氧系列存在以8、18、33、64个月变化的主要周期;高锰酸盐指数存在以9、20、31、50个月变化主要周期,以20个月尺度较为显著;化学需氧量存在以8、20、31、43个月尺度变化主要周期,以31个月尺度较为显著;氨氮存在以8、20、31、57个月尺度变化主要周期,以57个月尺度较为显著;总磷存在以8、12、23个月变化主要周期,以23个月尺度较为显著。综合来看,各水质指标具有多尺度振荡的特点,且主要存在以8、20、31个月变化的主周期,各水质指标主周期变化主要发生在汛期。
为探究主周期形成的主要原因,基于各指标多年平均值来分析各指标年内变化趋势,具体结果见图6。由图6可以看出,各指标在汛期(7—9月)含量明显低于年内其他月份,这可能是由于降雨量的增加,河段水流量也随之增加,会对污染物产生稀释作用,各指标含量降低,因而各指标呈现出汛期周期变化规律。

图6 各指标年内变化趋势
4.2 水质预测研究
基于上文的各个小波基和分解尺度对比分析结果,最终选择db2小波基对化学需氧量原序列s进行2层尺度的多分辨率分析,得到低频概貌分量ca2和高频细节分量cd2及cd1,见图7。

a)s
由图7可知,化学需氧量1年中的变化情况大致为夏季高、冬季低,春秋相当,但年际情况不尽相同。ca2与原序列最为接近,体现了化学需氧量的总体下降趋势,且在2005—2009年(第1—50月)波动较大,但具体细节变化未得到很好体现。cd2尽管为细节部分,但对原序列的一些峰值如第40个月仍有着较好的表达。cd1在峰值处呈现较大的波动,但更多地含有随机成分。
考虑到化学需氧量时间序列的长度,以及汛期周期变化的规律,最终选择以一整年12个月作为预测周期。即以2005—2017年(第1—156月)的月均化学需氧量数据作为训练对象进行训练,以2018年各月化学需氧量含量(第157—168月)作为最终预测对象。预测结果的误差分析见表4,预测值与实测值的拟合结果见图8。

表4 化学需氧量第157—168月预测结果误差分析

图8 化学需氧量预测值与实测值对照结果
由表4可知,在预测期内平均相对误差控制在8.4%,均方根误差为1.5。2018年1—6月(第157—162月)误差较小,7—10月(第163—166月)误差相对较大,7月份误差最大,可能与降雨量大小有关,因此在提高水质预测精度时,可以考虑加入季节性因素。图8可知,预测值与实测值的曲线变化趋势一致,尤其在短时预测时段拟合更优,总体来看,构建的小波神经网络模型预测化学需氧量精度较高,且较为稳定,能够适用于涡河流域的短期水质预测。
5 结论
基于涡河流域2005—2018年的水质指标月监测数据,即溶解氧、氨氮、高锰酸盐指数和化学需氧量,探究小波神经网络在流域水质污染中的应用。通过Morlet小波分析了涡河流域水质指标多尺度变化规律,并基于Daubechies小波和BPNN神经网络建立了小波神经网络预测模型,该研究结果证实了小波分析在水质时间序列变化规律及预测方面的可行性。
a)涡河流域水质指标的周期变化规律表明,总磷有3个主要变化周期,其他指标均具有4个变化主周期,各水质指标变化主周期存在一定差异,但主要存在以8、20、30个月左右变化的主周期,各水质指标主周期变化主要发生在汛期;目前涡河流域水质的主要影响因子是以化学需氧量为代表的,包括氨氮、高锰酸盐指数在内的第一主成分因子。
b)选择db2小波基对化学需氧量原序列进行了2层尺度的多分辨率分解;通过小波神经网络得到的化学需氧量预测值与实测值的曲线拟合度较高,平均相对误差为8.4%,均方根误差为1.5,该方法较适用于涡河流域的短期水质预测,对于水质预测具有较好的参考价值。
c)由于国内外缺乏最佳小波基的规范性选取方法,且研究发现季节性因素对水质序列预测误差影响较大,因而在今后提高小波BP神经网络预测精度时可以考虑从小波基的优化选择和季节性因素的输入出发。

