基于熵理论-可拓云模型的引水隧洞塌方风险评价
李 燕,靳春玲,贡 力,田 洁,朱桂勇
(1.兰州交通大学 土木工程学院,兰州 730070; 2.水利部海河水利委员会 引滦工程管理局,河北 迁西 064309)
1 研究背景
为均衡分配水资源,有效解决我国局部地区经济发展的缺水矛盾,国家投资建设了大量水资源配置工程,以促进缺水地区经济协调发展[1]。引水隧洞作为水电站的咽喉,在水资源配置工程中起着至关重要的作用。由于引水隧洞施工过程中塌方事故频繁发生,不仅在经济损失和人员伤亡方面产生重要影响,而且给工程留下了安全隐患,因此科学合理地评价塌方风险是引水隧洞施工阶段亟待解决的重要问题。
目前,相关领域专家和学者对隧洞塌方风险评价做出了卓越贡献。Zhang等[2]选取围岩级别、地下水条件、隧道埋深、开挖方法等构成评价指标体系,并以粗糙集理论和可拓学理论为基础,进行了塌方风险等级评价;Qiao等[3]通过现场调查和理论计算方法,研究了隧道塌方的机理,并根据现场监测数据提出了塌方区域的处理和评价方法;贡力等[4]通过主成分分析(Principal Component Aanalysis,PCA)法对建立的指标因素进行主成分提取,构建了概率神经网络(Probabilistic Neural Networks,PNN)预测评价模型;陈诚[5]基于TOPSIS法原理,建立了隧道塌方风险评价模型;杨光等[6]将云模型应用到塌方风险等级评价中,根据最大综合确定度确定塌方风险等级;李志强等[7]通过分析100多起塌方事故资料确定了影响塌方风险因子,并以Karwowski模糊隶属度函数基础,对隧道进行塌方风险评估。上述评价方法均在塌方评价中有所运用,虽然对隧洞塌方风险评价均作出了卓越贡献,但普遍存在计算量过大,实际操作性不强,权重计算仅依据专家主观知识和相关经验,未考虑评价指标的不确定性、不完整性、不精确性等问题,且部分方法未考虑塌方风险等级界限值的随机性和模糊性。
针对以上不足,本文基于云模型和可拓学理论构建可拓云模型,考虑风险等级界限值随机性和模糊性的同时,还能改善传统物元分析中将特征值被视为不动值的缺陷,目前该方法广泛应用于围岩稳定、施工安全评价等领域。同时,结合主、客观赋权法的优点,利用偏好比率法(Preference Ratio Method,PRM)和反熵权法(Anti-Entropy Weight, AEW)对指标因素权重进行分析,构成综合赋权法,使权重计算更具科学性,评价结果更为准确。最后结合珠江三角洲水资源配置工程中东莞分干线单线引水隧洞进行实例研究,论证本方法在引水隧洞塌方分析中的可行性。
2 基于PRM-AEW权重计算
2.1 基于PRM的主观权重确定
PRM是主观判定各评价指标重要度的方法[8],其原理是对所有指标进行两两比较,确定指标对评价结果的实际影响率,计算步骤如下。
2.1.1 确定偏好比率标度
假设指标si对隧洞塌方影响程度大于指标sj,则指标重要程度为si>sj,由此,主观定义指标间重要程度,得到指标间的偏好比率标度,如表1所示。

表1 偏好比率标度Table 1 Preference ratio scale
2.1.2 计算主观权重wi
在定义的偏好比率标度下,令指标si与sj间的偏好比率标度为gij(i,j=1,2,…,n),建立方程组(式(1))求解各指标权重wi。
式中gij为偏好比率标度值,0≤wi≤1(i=1,2,…,n),根据式(1)求解主观权重wi。
2.2 基于AEW的客观权重确定
反熵权法(AEW)是基于熵权法改进的一种赋权方法[9]。反熵权法特征与传统熵权法特征相反,当指标的无序程度越大时,说明指标包的含信息量越多,反熵值也越大,从而权重也越大[10]。具体计算步骤如下。
(1)计算各指标反熵值,即:
(2)
(3)
式中:hi为反熵值;vij(i=1,2,…,n;j=1,2,…,m)为指标值;rij为中间变量。
(4)
2.3 基于线性加权组合法的组合权重确定
主观赋权法代表了专家的直观认识,人为干扰因素较多;客观赋权法代表了指标实测数据的客观规律,但缺少专家的主观意向;因此,将两类权重方法进行组合得到更加科学、合理的综合权重是极为重要的。目前的组合方法有因子相乘法、离差最大化法和线性加权组合法等,因子相乘法易产生“倍增效应”,离差最大化法适用指标评价值之间差异较大的情况。本文采用线性加权组合方式[11]将主客观权重进行组合,其公式为
(5)
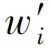
为合理准确分配系数,引入基于加权求和最优化模型,模型为
s.t.α2+β2=1 ,α、β≥0 。
(6)
该模型最优解为:
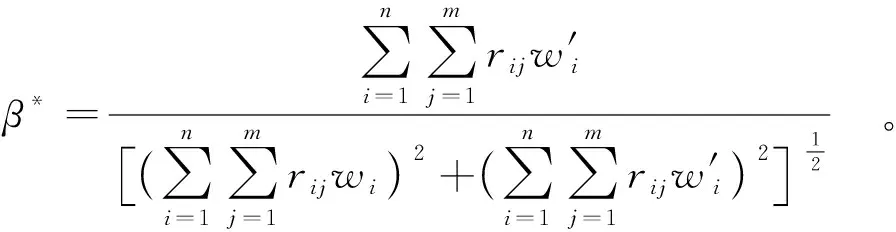
(8)
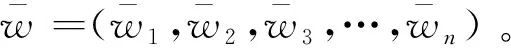
3 基于熵理论-可拓云理论评价模型的计算步骤
3.1 云模型理论
云模型是由李德毅教授提出的一种即能反映客观事物的随机性和模糊性,又能实现评价指标与评价等级间的确定和不确定关系的统一定量描述的模型[12-13]。其定义如下:假设某研究对象评价指标有n个(i=1,2,…,n),评价等级有m个(j=1,2,…,m),评价指标i对应第j等级的云模型可由云滴数N和数字特征(Ex,En,He)来产生,云模型数字特征计算模型为:
(9)
(10)
He=s。
(11)
式中:Cmax、Cmin为各等级的上下界限;Ex代表各等级期望值,表示隶属云的分布中心,是最能代表引水隧洞对应等级界限概念的样本点;熵En是对概念的不确定性描述,不但能描述引水隧洞塌方风险等级评价过程中采集样本数据的随机性,而且还能描述塌方风险等级界限的模糊性[14];超熵He是对熵的不确定性的量度,一方面反映了引水隧洞塌方风险等级样本数据的离散度,另一方面体现了风险等级级评价中各指标的随机性和模糊性之间的联系度。
3.2 可拓云理论
可拓学理论是由蔡文教授提出的一种解决矛盾问题的形式化理论方法[15],其基本物元模型为R=(对象N、特征C、量值V)。传统的物元分析模型中,一般将特征值V被视为不动值,从而忽略了事物的模糊性和随机性[16]。本文结合云理论处理不确定性问题的随机性和模糊性,用正态云(Ex、En、He)代替特征值V,则可拓云模型表示为
(12)
3.3 云关联度计算
(1)标准等级可拓云与指标量值间的关联度k的计算方法为
(13)
式中:En为各等级的期望值,En′~N(Ex,En2);χ为某指标量值。
(2)通过式(13)计算所有指标关联度,并构成如下的矩阵K,即
(14)
式中:Kij为待评指标和塌方风险等级j的标准云之间的云关联度;n为评价指标的个数;j为评判级别。
3.4 基于信息熵的隧洞塌方风险等级评定
(15)
式中ph为云关联系数的分布密度,h=1,2,…,10。
(2)引入信息熵理论[17],云熵的定义为
(16)
(3)设云熵的最大值为Hmax,隶属度K(kj)的计算式为
(17)
3.5 隧洞塌方风险等级评定检验
(1)计算综合评判向量H,即

(18)
(2)计算评判的模糊等级特征值f,即
fi=hiti。
(19)
式中:hi为向量H对应最大分量;ti为最大分量对应等级。
(3)多次运算求解,减少随机性。为尽量减少随机数值所带来的不确定性的影响,故需多次求解。经多次运算得出综合评判矩阵Kx、等级特征期望Efx和等级特征熵值Efm,其表示式分别为:
(20)
(21)
(22)
式中:h为运算的次数,本文取500;K(i)为第i次运算得出的综合评判矩阵;fi为第i次运算得出的等级特征值;期望值Efx表示塌方风险等级;熵值Efm表示评价结果分散度。
可信度θ由式(23)进行定量表达。θ值越小表示可信度越高。
(23)
4 工程实例应用
4.1 工程概况及评价指标
珠江三角洲水资源配置工程是广东省历史上投资数额最大、输水线路最长、受水区域最广的水资源调配工程。该工程由输水干线、深圳分干线、东莞分干线和南沙支线组成,输水线路总长113.2 km。东莞分干线长3.5 km,设计流量15 m3/s,网河区西部至东部单线引水隧洞总长为8.453 km,隧洞地表多为建筑物密集区。区间地质水文条件复杂,地下水类型以孔隙性潜水为主且水位普遍埋深较浅,多0.5~3 m,局部丘陵地带以基岩裂隙水为主,一般埋深2.0~5.0 m,围岩主要以Ⅲ、Ⅳ级围岩为主,围岩自稳时间短,极易产生塌方与变形破坏。为尽可能避免引水隧洞在施工期发生塌方风险,减少风险带来的损失,本文在普通引水隧洞施工可能发方生塌方风险的影响因素的基础上,考虑了该区域复杂的地质水文情况,并参考《水工隧洞设计规范》《水工隧洞安全监测技术规范》及已有文献资料[5]等,从工程地质因素、水文地质因素、施工设计因素3个方面建立评价指标体系,引水塌方风险评价指标体系如图1所示。

图1 引水隧洞塌方风险评价指标体系Fig.1 Risk assessment index system for diversion tunnel collapse
(1)工程地质影响因素。岩石单轴饱和抗压强度反映了隧洞围岩软硬程度,围岩抗压强度越高,塌方风险越小;岩体完整性指数体现了岩体的完整程度,与塌方风险成正比,即岩体完整性越好,塌方风险越低;偏压是由于隧洞洞口浅埋段受地形作用而产生,并对围岩稳定性有一定影响,一般情况下,山体倾角越大,塌方风险越高;节理面间距是影响洞室岩体渗透性及稳定性的关键因素,节理面间距越小,岩石破碎程度越大,塌方风险越高。
(2)水文地质影响因素。水是引水隧洞发生塌方事故的主要影响因素,地下水通过渗透带走细小颗粒,导致岩块软化,使得岩体强度降低;在节理较多的岩体中,水的存在会很大程度上减小节理间的摩擦效果;地下水动能和静压的总和称为地下水水头,一般来说,地下水水头压力越大,塌方风险越大。
(3)施工设计影响因素。引水隧洞开挖跨度与塌方风险成正比,开挖跨度越大,岩体受扰动节理组数越多,进而岩体碎程度越大,隧洞围岩稳定性越低;引水隧洞埋深与塌方风险成反比,隧洞埋深越浅,其开挖对围岩的破坏程度越大,围岩自稳能力越差,容易产生大变形。
参照国内外隧洞塌方风险等级划分标准及《铁路隧道风险评估与管理暂行规定》中的风险等级划分标准,本文将塌方风险划分为低度(Ⅰ)、中度(Ⅱ)、高度(Ⅲ)、极高(Ⅳ)四个等级。其中,其中I级风险表示风险可被忽略,不需要有针对性地采取风险处理措施;Ⅱ级风险表示风险在预期范围内,对潜在风险可采取合理措施阻止或降低事故造成的影响;Ⅲ级风险表示风险超出预期,必须采取合理措施降低风险并加强日常检测;Ⅳ级风险表示风险最高,必须给予高度重视并规避,否则不惜成本将风险降低至期望程度。隧洞塌方风险等级的具体划分标准如表2所示。

表2 隧洞塌方风险评价指标分级标准Table 2 Classification standard of risk assessment index for diversion tunnel collapse
4.2 工程数据
本文选取该段引水隧洞中的9段典型隧洞进行塌方风险分析,得出各段隧洞塌方风险状况,具体数据如表3所示。

表3 隧洞塌方风险实例样本量化数值Table 3 Quantified values of tunnel collapse risk of samples
4.3 运用PRM-AEW确定各指标权重
4.3.1 PRM计算主观权重
为保证指标权重的可靠性,共邀请10位长期从事于引水隧洞设计、施工、管理方面的专家,根据其自身经验和知识,独立地对表1中10项指标进比较,得到各评价指标间的偏好比率判断:
据式(1)得出9段隧洞的主观权重为
W=[0.219 3,0.145 7,0.099 5,0.076 2,0.130 6,
0.095 8,0.036 3,0.092 2,0.078 3,0.026 1]。
4.3.2 AEW计算客观权重
将表3中隧洞塌方数据代入式(2)中,得到各评价指标的反熵值为
H=[1.784 5,1.059 9,1.321 3,1.368 8,1.161 9,
1.142 5,1.196 0,1.166 5,1.268 7,0.515 7 ]。
再由式(4)可进一步求得各个评价指标的反熵权为
W′=[0.148 9,0.088 5,0.110 2,0.114 2,0.096 9,
0.095 3,0.099 8,0.097 3,0.105 9,0.043 0]。
4.3.3 综合权重计算
根据式(5)—式(8)建立加权求和最优化模型,求得综合权重为

0.095 5,0.074 4,0.095 3,0.094 8,0.036 3]。
4.4 综合评价等级的计算
(1)通过上述塌方风险评价指标分级标准表及式(9)—式(11)计算得到的Ex、En、He,描述出安全等级界限云模型,如表4所示。
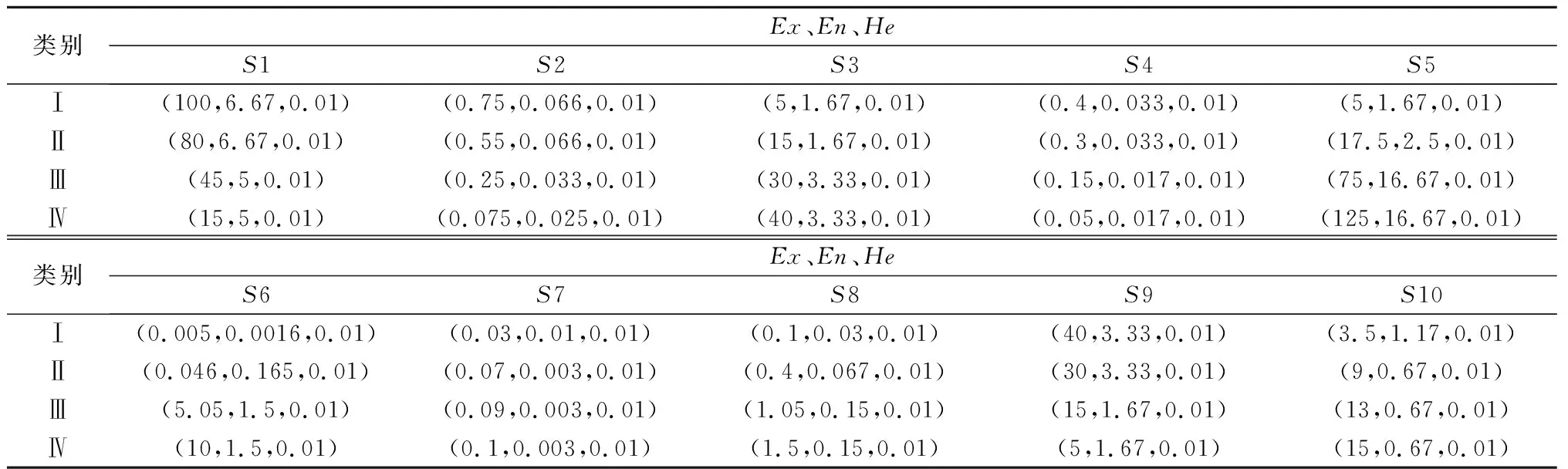
表4 隧洞塌方风险因子的云模型数字特征Table 4 Digital characteristics of cloud model of tunnel collapse risk factors
(2)隧洞塌方评价因子云模型数字特征确定后,运用MATLAB绘制所有指标的评价云图。其中,图4中的(a)、(b)、(d)、(i)图从左往右依次Ⅳ—Ⅰ级,(c)、(e)、(f)、(g)、(h)、(j)图从左往右依次Ⅰ—Ⅳ级,具体云图如图2所示。

图2 隧洞塌方风险因子评价等级云图Fig.2 Cloud map of assessment levels of tunnel collapse risk factors
(3)通过MATLAB编程计算出各评价对象塌方风险等级最大隶属度,并得到各评价对象塌方风险级别与相应置信度因子,具体计算结果如表5所示。同时为验证该模型的可行性,采用TOPSIS法对珠江三角洲水资源配置工程中东莞分干线单线引水隧洞的9段典型隧洞进行塌方风险评价,得到各塌方等级典型样本与与正理想解的贴近度E+(Ⅰ级塌方风险,Ei+=1;Ⅱ级塌方风险,0.490 4≤Ei+≤1;Ⅲ级塌方风险,0.307 1≤Ei+≤0.490 4;Ⅳ级塌方风险,0≤Ei+≤0.307 1),将评价结果进行对照。
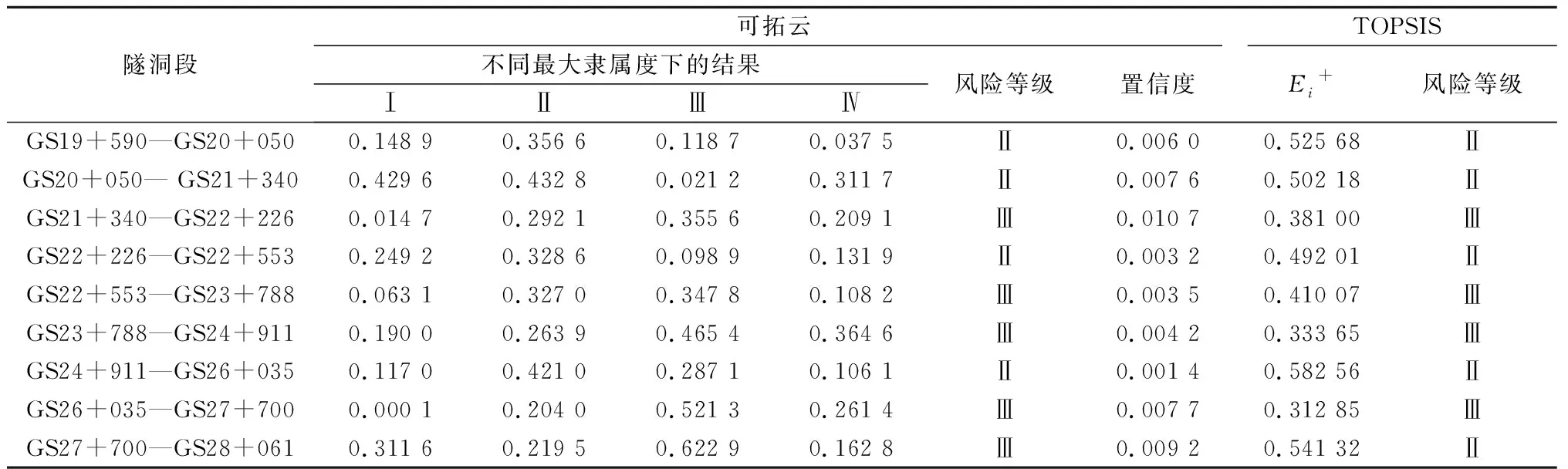
表5 塌方风险等级评价结果Table 5 Assessment results of collapse risk level
通过计算得出GS21+340—GS22+226、GS22+553—GS23+788、GS23+788—GS24+911、GS26+035—GS27+700及GS27+700—GS28+061五段隧洞塌方风险等级为Ⅲ级。根据引水隧洞工程实际情况,GS21+340—GS22+226、GS22+553—GS23+788、GS23+788—GS24+911、GS26+035—GS27+700及GS27+700—GS28+061五段隧洞水文地质复杂,塌方影响因素多,风险较大,在施工过程中必须采取风险处理措施降低风险并加强检测,具体措施有:地表注浆加固、超前小导管预注浆、三台阶临时仰拱法施工等。GS19+590—GS20+050、GS20+050—GS21+340、GS22+226—GS22+553和GS24+911—GS26+035四段隧洞塌方风险等级为Ⅱ级,属于中等风险,根据引水隧洞工程实际情况,GS19+590—GS20+050、GS20+050—GS21+340、GS22+226—GS22+553和GS24+911—GS26+035四段隧洞地质情况属于中等复杂,存在一定的塌方风险,施工过程中需要采取合理处理措施来降低风险。
5 结 论
(1)考虑到各指标因素间的关联影响性,采用偏好比率法(PRM)和反熵权法(AEW)分别计算主客观权重,并采用线性加权组合方法计算组合权重,既避免了人为因素的过多干扰,又排除了因客观因素占比过大,导致准确性降低,使权重的计算更具科学性。
(2)结合隧洞塌方风险评价指标体系,提出了基于熵理论-可拓云模型的引水隧洞塌方风险评价方法,不仅全面考虑塌方风险等级界限值的随机性和模糊性,而且对工程原始数据直接进行利用,避免了对数据进行归一化处理的过程,同时减少了信息丢失的可能性。
(3)将熵理论-可拓云模型应用到珠江三角洲水资源配置工程中的东莞分干线单线引水隧洞,经评价:GS19+590—GS20+050、GS20+050—GS21+340、GS22+226—GS22+553和GS24+911—GS26+035四段隧洞评价等级为Ⅱ级,需要采取合理风险处理措施来降低风险。GS21+340—GS22 +226、GS22+553 —GS23+788、GS23+788—GS24+911、GS26+035—GS27+700及GS27+700—GS28+061五段隧洞评价等级为Ⅲ级,风险较高,在后续施工中必须采取风险处理措施降低风险,减少塌方事故造成的损失。该评价模型操作简单,便于实施,且适用性强,今后可运用于引水隧洞塌方风险评价中。

