借助几何直观 构建“讲道理”的课堂
——以罗鸣亮老师执教的“小数的意义”一课为例
郑璘玲
(福建省莆田市荔城区第三实验小学)
“小数的意义”一课是典型的概念教学,在小学数学教学体系中占有非常重要的位置。福建省普教室特级教师罗鸣亮在其执教的“小数的意义”课堂上,充分利用了学生已有的生活经验,通过依次拆开“神秘的信封”活动,追本溯源,恰当地利用标准图形和变式图形,引导学生逐步挖掘隐藏在“小数”背后深层次的数学之“理”,带领学生探究“小数”形成的全过程,活化了数学思维,构建了“讲道理”的数学课堂。
一、问题引领,思之有“源”
认知冲突是学生思维的“催化剂”,通过创设认知冲突,能激发学生的数学思维,使学生产生数学学习的动力。在教学中,可以通过问题来引发学生的认知冲突,使他们在解决问题的过程中去思考,通过思考掌握数学知识的本质。
上课伊始,罗老师依次抽出一个装有若干个红色正方形的“神秘信封”。
师:我带来了几个正方形。大家数一数看,一共有多少个?
生:1、2、3个……10个。
师:10个10个地数。
生:10个、20个……100个。
数着数着,只见罗老师不慌不忙地从信封中取出一个与之前形状和大小一样、但涂色面积不同的正方形(如下图所示),并提问:这个图形中的涂色部分表示多少个正方形呢?

学生一时没有了头绪,纷纷表示不理解。心中产生了问题:如果说之前出示的正方形,每个正方形表示“1”个单位,那么这个正方形的涂色部分又该表示多少个正方形呢?直觉是在丰富知识经验的基础上,在短时间内直观地把握事物的本质,瞬间做出判断的思维形式。而数学意义上的直觉是人脑对数学对象、结构、关系以及规律性的某种直接领悟或洞察。数学直觉尽管“突如其来”,但也是立足于已有知识经验和数学思考的,是“有一定根据的”。如何让学生“推之有据”?在传统的教课堂教学中,不少教师常担心学生不理解自己的用意,怕他们的思维出“岔道”而迷路,浪费宝贵的课堂时间。因此,他们喜欢把解决问题的思路讲明白,在学生脑海中尚未形成问题意识之前,就急于过早地亮明“路标”,希望把学生的思路引向预期的答案。这样做不仅限制了学生思维的活跃度,也使其自我探索的兴趣尽失。学生一旦思路变得狭窄,就会产生学而无惑、学而无味的感觉。罗老师这时并没有急于亮出答案,而是让学生继续思考,积极寻找猜想的依据、思考猜想的合理性。
师:出了什么问题?
生:我发现这个正方形上不全是涂着红色,有一部分是涂着白色。
师:也就是说,这个正方形还能用1来表示吗?
生:不能。
师:怎么办呢?
生:用小数。
此前,学生虽已学习了“分数的初步认识”和“小数的初步认识”,头脑中对分数、小数的概念已有一定认知,但对小数、分数与整数之间的有机联系依然不清楚。面对不完整的正方形,如果一味试图用整数来解决问题,必然会遇到无法克服的困难。一张不完整的正方形卡片,巧妙地为学生创设了一个真实的、与学生现有知识水平有“冲突”的、合情合理的教学情境。用问题“还能用1 来表示吗?”又一次引发了学生的议论和思维碰撞。在教学中,渴求知识的学生会因挑战而睿智,因认知冲突而生动,有效的课堂会因“讲道理”而出彩。此时,学生对“不一样”的正方形所产生的质疑,正是需要开发的宝贵教学资源。
二、追根溯源,探之有“据”
在课堂上要有意留给学生充分的思维时空,循序渐进,由浅入深,以问题冲突为导索,让学生自己学会“抽丝剥茧”,一步步深化探究,借助问题冲突“讲道理”,用“问题之钥”开启“问题之锁”。
罗老师出示一张“十等分”中涂色占“三分”的正方形,并提出问题:你会用哪个小数来表示它?
生:0.3。
(罗老师先板书0.3,再出示一张“十等分”中涂色占“七分”的正方形)
生:0.7。
师:数一数,一共有几个这样的数?
生:0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9。
师:0.9加上一个0.1,就是1。
(罗老师又出示一张之前“未知”的正方形,让学生通过比较估测那张正方形中涂色部分占“几分”)
生:我觉得0.5不可能,因为白色部分少于一半,不止0.5。
师:到底是多少呢?
生:既然我们能用十分之几表示一位小数,同样也可以把一个正方形平均分成100 份,用百分之几表示两位小数;还可以平均分成用1000份,用千分之几表示三位小数。
罗老师为了引导学生追根溯源,梳理小数发展的历史脉络,探明小数的产生过程,将小数作为自然数的外延,从辨认一张不一般的正方形入手,直观又自然地引出结论:不满“1”的一位小数可利用“平均分”法,进行十等分、百等分、千等分……帮助学生深入理解了小数的意义,建立起小数意义的模型。
三、数形结合,推之有“理”
学生懂得了小数源自“十进分数”的理论之后,为了加深理解,继续挖掘小数概念的内涵,罗老师抓准学生认知结构中的混淆点、易错点和缺失点,挑选出比较0.9 与0.90 异同点这个挑战性题目,为突破难点开辟了一个新视角,再次引发学生的认知冲突,让学生不知不觉落入问题“陷阱”。然后,又在0.9 的后面补了一个零,并提出问题:到底是0.90还是0.9 呢?
生:0.90。把正方形“十等分”,现在涂红色的占9份,所以是0.9。
生:把一个正方形平均分成了100 份,涂满了90份,所以是0.90。
生:我觉得0.9 和0.90,它们代表的部分是一样的。平均分成100 份、涂90 份,相当于平均分成10份、涂9份的部分。
师:0.90后面添了一个0。如果不添,可以吗?
生:可以。
师:为什么不添0也可以呢?
生:因为0.9和0.90表示的份数都一样。
生:老师,我觉得不可以,因为0.9是直接把这个正方形平均分成10份,取其中的9份,但现在这个正方形是取其中的90份,份数不同。
生:0.9 表面上可以。如果是1 米长的线段,0.9代表的是9 分米;如果是0.90 的话,它代表的是90 厘米。90厘米等于9分米,所以应该是可以的。
生:我觉得不可以。因为它们表示的是份数不一样,虽然它们所占的量与它们填满的部分都一样,但是它们平均分成的份量不同。
师:它们表示的大小是不是一样的?
生:是一样的。
短短40 分钟的课堂,罗老师不忘适时、适度地渗透“数形结合”这一重要的数学思想方法。小数的十分进制兼有“数”的严谨与“形”的直观,充分体现了数学教学中最精彩的一面。利用它能使复杂变得简单,抽象变得具体。以简洁、合理、科学为原则选取十进制,与整数“满十进一”的规则对接,形成一个整体。通过精心设置,引导学生深入挖掘,一步一步根据算理去思考,深刻认识和理解了每相邻计数单位之间的十进制关系,建构起了小数数位顺序表,并在整数数位表上顺利衔接延续。
四、直觉判断,解之有“法”
小数产生的本源在于计量的需要,并非由分数改写而成的。罗老师又提出了“为什么要把‘1’平均分成10 份,而不是9 份或11 份呢”的疑问,让原本单一、枯燥的概念教学,在新知识的生长点处又引发出新的“认知冲突”。
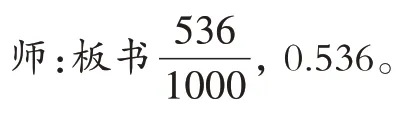
师:你觉得罗老师是要把它平均分成1000份,然后涂上536份吗?
生:平均分成600份,取其中的536份。
生:不行,不能平均分成600 份,而要是分成1000份,分得又太多了。
生:先把它平均分成10份,然后在分3和6时,把它再平均分成10份。
师:你的的意思是0.536中有5个0.1。
生:0.536中,有3个0.01。
生:0.536中有6个0.001。
通过类比,层层剥离,让学生终于解开了“如果分成9份,分成11 份,会便利吗”的问题。
罗老师的课堂,除了能在教学新知识生长点时对概念内涵巧设“陷阱”,还能在教学新知概念的外延上捕捉认知冲突,诱发学生在认知的“平衡”与“不平衡”间进行充分地争议,在争议中暴露出学生的“错误”认知和思维缺陷,从而完善认知,提升思辨能力。
师:再想一想看,那么多三位小数,罗老师为什么偏偏不带其他来,只带一个0.536 来呢?想一想并猜一猜,0.536和我有什么关系?
生:老师,会不会是你的生日?
师:你觉得我的岁数是小数吗?
生:我想这是你办公室的门牌号。
师:有把门牌号写成小数的吗?
生:老师,我猜你是5点36分生的?
师:年、月、日、门牌号,还有出生的时间,用小数表示,有意义吗?
生:身高是536厘米,还是536毫米?
师:请来看一看,0.536 会是罗老师的什么呢?其实,0.536 米是罗老师的手臂长度。请看大屏幕(播放课件出示数轴)。
师:我的身高在数轴上,能找得到吗?
师:1.73米。那么,40年后的身高呢?
生:40年后会是1.83米。
师:40 年后就不到1.73 米了,这是由于人变老了。
生:40 年后的身高可能没有现在这么高了。因为人老了就会变矮。
师:说得好,这是自然规律。
在猜想“0.536”的过程中,学生可以直观地领悟到“一个小数,数位不同,位值也就不同”,感知小数在实际生活中应用的适应性和广泛性。
最后,罗老师又一次借助“数形结合”,用数轴亮出谜底作为总结,让学生在数轴上找整数、分数、也找小数,实现了数与形的真正“联姻”,帮助学生在认识数序的同时,亲身体验自然数、分数和小数及其之间的互化、大小、内在关系,使抽象的数变得有“形”可依。

