融合CZT频谱细化算法的InSAR相位滤波方法
张继超,李继虎,赵鹏飞,林泓全
(1.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000;2.辽宁工程技术大学 软件学院,辽宁 葫芦岛 125105)
0 引言
合成孔径雷达干涉测量技术广泛应用于大区域的地表高程反演和长期形变监测,其原理是通过对同一地表区域多次观测的SAR影像进行干涉,从而获取较高精度的干涉相位信息,干涉相位图的质量直接决定干涉相位测量的精度。在InSAR干涉测量中,由于地表环境复杂、大气环境因素导致的传感器接收地表信号不佳和受到热噪声去相干、时间去相干、基线去相干以及信号去相干等多种因素影响而产生噪声复杂区域,在滤波效果较差的情况下会导致解缠过程中由于产生较多奇异点使得相位解缠精度下降,甚至无法解缠,而且还会导致后续衍生产品质量不佳[1-2]。因此,为了减小噪声对干涉测量结果产生的负面影响,并保证干涉测量结果的准确,在相位解缠之前对干涉相位进行适合的滤波是必不可少的。
现阶段,用于干涉相位滤波的方法大致分为频率域滤波和空间域滤波。空间域滤波主要有均值滤波、中值滤波和圆周期均值等方法,其原理简单、运算速度快,但没有考虑干涉相位图的实际含义,滤波效果不尽人意,而且在滤波窗口的选择上有一定难度,在干涉条纹密集区域容易破坏细节,出现失真的情况。随着空间域滤波的发展,又有学者将自适应滤波和自适应窗口大小的滤波方法等相关技术应用于干涉相位滤波中,例如精细Lee滤波,通过自适应的方法可以根据图像的纹理特征相似性来更好地消除噪声并保留图像中的细节,但其计算复杂,而且仍旧无法很好保留干涉跳变信息[3-4]。频率域滤波是将图像变换到频率域,通过去除高频噪声部分从而实现滤波[5]。1998年,Goldstein和Werner提出了一种在频率域中的自适应干涉相位滤波方法,这一具有里程碑意义的滤波算法是采用傅里叶变换将干涉相位变换到频率域平滑处理,再将平滑后的频率域干涉相位做傅里叶逆变换回到空间域。经典Goldstein滤波是典型的干涉相位滤波方法,它在去噪与保持影像分辨率的效果较好,但在选取参数主观因素较强。在2003年,Baran等[6]将Goldstein滤波的滤波参数根据两张SAR影像的相干性系数相联系,使之可以根据相关性的好坏自动地改变滤波参数,从而改变滤波强度,使得传统滤波效果进一步提升。2019年,Hensley[7]用Goldstein与Werner滤波结合的方法来解决因长时间、长基线引起的对噪声的影响,但该方法在噪声复杂区域去噪效果不佳,使得在高噪声区域滤波质量仍然不高。
为了更有效抑制噪声复杂区域,并保持条纹密集区域的信息不被破坏,以达到滤波结果有利于解缠和提升干涉测量精度的目的,本文提出了一种融合频谱细化和自适应Goldstein相位滤波的方法,将图像转换至频率域后,通过线性调频Z变换(CZT)的方法进行局部的频率估计,提高计算的频率分辨率,使得在高噪声区域的频谱得以细化以达到更好区分噪声与实际有用相位信息的目的;通过自适应的方式,可根据相干影像的相关性改变滤波强度,以达到去噪与保留条纹密集区信息的兼顾。将本文方法与Boxcar滤波、非局部均值滤波(non-local means,NL-Means)和自适应Goldstein滤波进行对比,通过仿真实验与实际数据验证本文方法的有效性。
1 融合频谱细化的自适应滤波原理
1.1 线性调频Z变换频谱细化算法原理
如果说N点的快速傅里叶变换是在Z平面的单位圆上的等间距取N个点,那么CZT则是Z平面螺旋线的周线上Z变换取等间距N个点[8]。CZT频谱细化可以计算在N点中输入数列为x(n)的给定一条路径的Z变换,采用增加输出点数,使得输出点多余输入点数就可以达到对指定频谱细化的目的[9-10]。
假设采样序列x(n),n=0,1,…,N-1中,采样频率为fs,其中f1~f2为需要细化的频谱条带,对信号进行N点快速傅里叶变换,故有原有信号的频率分辨率为Δf=fs/N,所选需要细化条带中心频率为f0=(f1+f2)/2,带宽为fw=f2-f1。用X(z)来表示x(n)序列的Z变换,通过CZT算法就可以计算给定点Zk上的Z变换X(Zk)。
Zk=AW-k,k=0,1,…,M-1
(1)
式中:A=A0e-jθ0;W=W0e-jφ0;M为所要分析复数频谱的采样点数;j为虚数。其中,A0和θ0分别表示第一个采样点Z0的矢量半径的大小与相角;W0为Z平面螺旋线的伸展率;φ0表示相邻采样点间的角度差。根据式(1)所给的Zk值,推导可得Z变换X(Zk),如式(2)所示。

(2)
令
(3)
(4)
可得
(5)
令
(6)
可得
(7)
在实际过程中,频带点的采样点数M需要根据整个频谱的频谱分辨率Δf′来确定,它们之间的关系满足公式:Δf′=fw/(M-1)。由于此次频谱分析在单位圆上进行CZT算法的实现,因此A0与W0取1,θ0=2πf1/fs,φ0=2πΔf′/fs。
1.2 自适应Goldstein算法模型
Goldstein滤波算法是基于一种傅里叶变换的自适应滤波方法,将干涉相位转换至复数形式,有效避免干涉相位图在相位跳变处的影像,并在空间域进行处理滤波。其滤波算法过程[11-13]如下所示。
将干涉相位图(x,y)转换为复数形式的矢量空间E(x,y),如式(8)所示。
E(x,y)=exp(φ(x,y))=cos(φ(x,y))+j·sin(φ(x,y))
(8)
选定合适滤波窗口大小,对E(x,y)进行二维快速傅里叶变换到频率域Z(u,v)(其中u,v表示空间频率),并进行Goldstein滤波处理得到H(u,v),如式(9)所示。
H(u,v)=S{|Z(u,v)|}α·Z(u,v)
(9)
式中:S{}为滤波平滑算子;α(0≤α≤1)为过滤器参数。当过滤器参数α=0时,不对其进行平滑滤波,当α的值过大时,滤波结果将会在相位跳变密集区过度滤波,使得精度下降。为了提高滤波效果,α的取值将根据两张SAR影像的干涉相关系数,即α=1-r(0≤r≤1)。最后将经过滤波后的频率域H(u,v)做二维快速傅里叶逆变换得到滤波后的结果。
这种使用相干性系数作为过滤器的平滑参数的特点是在相干性好的区域可以防止过度滤波,从而使干涉图的分辨率降低,而在相干性差、噪声多的区域增强滤波效果,达到对噪声更好的过滤。
1.3 基于融合CZT频谱细化的自适应滤波方法
由于传统的频域滤波方法在相对较低的频域分辨率中分辨有用信息与噪声的能力有限,为了能够将这些噪声复杂区域进行良好的滤波,同时保持干涉条纹紧凑区域的信息不被破坏,本节结合了上述CZT频谱细化和自适应Goldstein滤波方法的特点,提出了CZT频谱细化与自适应滤波相融合的方法。通过CZT频谱细化的方法细化相位干涉频率域的频率分辨率,区别噪声频率与有用信息相位的频率界限,并根据两幅干涉的主副影像在噪声复杂区域相关性较差,条纹密集区有着较高相关性的特点改变滤波参数的大小实现在噪声复杂区域滤波良好的同时尽量减小对条纹密集区细节的丢失。其具体算法流程如下。
步骤1:首先将干涉相位转换至矢量空间,使得跳变的不连续的相位变成连续的复相位数据,通过式(8)得到复干涉相位E(x,y)。在一个复干涉相位的小窗口内(窗口大小为Na×Nr),相位变化的坡度可以认为是近似相等的常数,即通过快速傅里叶变换将复干涉相位转换到频率域中的仅有的一个主频,这个主频对应的相位如式(10)所示。
φ(m+p,n+q)=2πp·fa+2πq·fr+φ(m,n)
(10)

步骤2:针对复干涉相位转换到频率域中的频谱峰值作为主瓣始点进行频谱细化,通过式(1)至式(7),对计算窗口的方位向与距离向取3×32个采样点做CZT变换,对主频谱瓣进行32倍采样估计,可得式(11)。
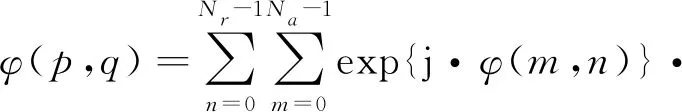
(11)


(12)
则在这个小窗口内的线性相位细化频谱如式(13)所示。
ih=0,1,…,Nr-1
(13)
步骤4:根据细化后的复干涉相位频带做自适应滤波(式(14))。
(14)

根据上述步骤原理,其流程图如图1所示。

图1 本文干涉相位滤波方法流程
2 实验方案与评价指标
2.1 实验方案
通过仿真实验与实测数据来验证本文提出的方法。其中,仿真数据来源于MATLAB软件中peak函数生成的理想干涉图(图4(a))与添加了真实SAR影像噪声的仿真干涉图(图4(b)),用来模拟真实噪声的影响。实测数据来源于将Sentinel-1A的单视复数影像通过ENVI软件中的SARscape模块通过裁剪、配准等预处理所产生的干涉图(图7(a))。为了验证本文滤波方法的有效性,将本文方法与Boxcar、NL-mean和自适应Goldstein滤波方法作对比,从目视结果、相位残差点数量、相位导数标准差以及仿真实验误差的角度进行分析。实验方法流程如图2所示。
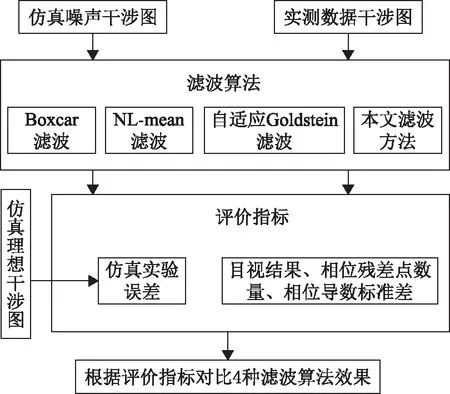
图2 实验方案流程
2.2 评价指标
为了更好地对比相位滤波效果,本文除了在目视效果上作对比外,还加入了相位残差点与相位导数标准差作为对比依据,并且在后续的仿真实验中对比了这几种滤波方法的误差效果。
相位残差点的多少将直接影响相位解缠的质量,滤波后相位残差点的数量越少,对相位解缠的效果越有利,其解缠的精度越高[14-15]。
相位导数标准差是评价干涉图质量的有效方式,其值越大,说明干涉效果越差。
3 实验结果分析
3.1 仿真实验
为了更准确地对比实验结果,本节使用仿真模拟干涉相位来对比本文滤波方法和其他3种相位滤波的提升效果。本小节仿真模拟相位图由MATLAB软件的peaks函数生成,大小为512×512,如图3(a)所示。模拟真实SAR影像噪声的仿真干涉相位图如图3(b)所示。图3(c)至图3(f)是4种滤波结果图。通过这4幅滤波结果图,可以较为明显地判断出Boxcar滤波与NL-mean滤波去噪效果较差,自适应Goldstein滤波与本文方法滤波效果较好。为了更好地显示4种滤波方法在条纹密集区的滤波效果,图3(g) 至图3(j)给出了4种方法在图上标出的条纹密集区滤波结果放大图。可以看出,本文方法在去噪效果与干涉密集条纹保持情况相较于其他3种滤波方法更好。
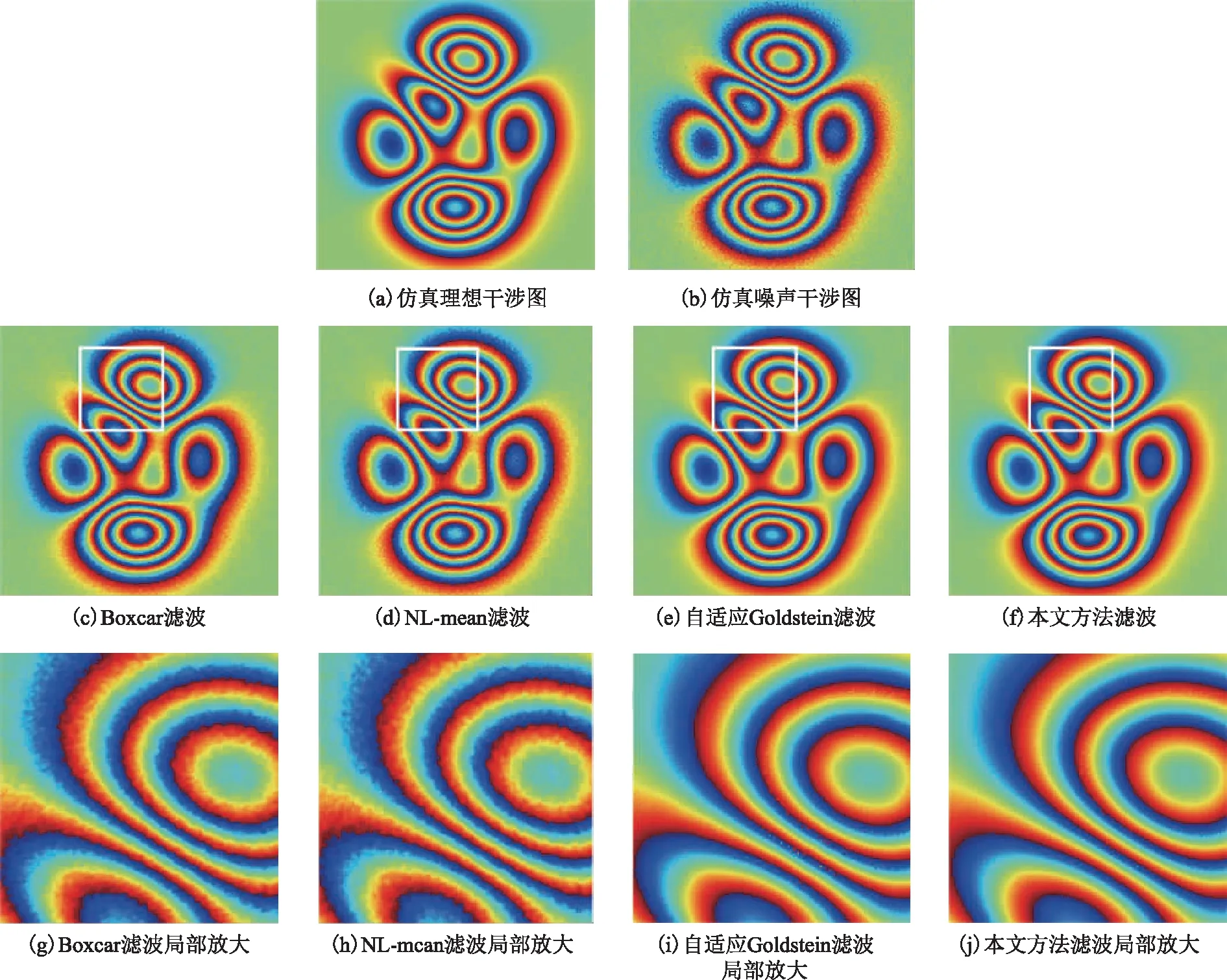
图3 仿真数据及模拟干涉相位图滤波结果与条纹密集区滤波放大图
此外,通过对比4种方法滤波结果的相位残差点数(表1),不论在全局区域还是条纹密集区域,本文研究的滤波方法明显少于另外3种滤波方法,这也意味着该方法更有益于后续的相位解缠阶段。图4表示4种滤波方法的相位导数标准差统计情况。从相位导数标准差统计图可看出本文研究方法相对于其他3种方法的相位导数标准差值的数量更靠近0,表明本文方法滤波结果的干涉图质量相较于另外3种方法有不同程度的提升。从仿真实验的误差统计图(图5)可以看出,这4种滤波方法的误差结果都呈现近似正态分布,而本文滤波方法在全局区域和条纹密集区的误差所呈现的正态分布尖峰更高,证明本文方法在全局区域与条纹密集区域的滤波精度相较于其他3种方法有所提升,证明本文方法在去噪效果与保持条纹密集区域的信息上有更好效果。

表1 不同滤波方法结果的相位残差点数量

图4 4种滤波方法的相位导数标准差统计对比

图5 4种滤波方法结果及条纹密集区滤波结果的误差统计对比
3.2 实测数据实验
本节使用的实测数据为哨兵1号SAR影像数据,选用2018年12月12日与2018年12月23日福建省泉州市某区域裁剪后的影像进行干涉,截取了600像素×600像素大小的干涉区域作为实验对象。所选区域为多山且林区密集,干涉形成的噪声较为复杂且干涉条纹比较密集有利于进一步验证本文算法良好的去噪能力与保持条纹细节信息的能力。图6为实测数据和4种方法的滤波结果。可以看出,在相同大小13×13的滤波窗口条件下,Boxcar与NL-mean滤波方法在去噪能力上较弱,自适应Goldstein滤波无法较好地保持条纹细节,而本文滤波方法在良好去除噪声的同时保证了紧凑条纹信息能够较好保存。此外,在表1所示不同方法滤波结果所含残差点数目中,本文滤波结果后的残差点最少,更利于相位解缠。图7和图8分别对比了4种方法的相位导数标准差及其统计图,本文滤波方法由于相位导数标准差值更多地趋向于0,因此,本文滤波方法优于其他3种滤波方法。

图6 实测数据和4种滤波方法结果

图7 实测数据和4种滤波方法干涉结果的相位导数标准差图对比
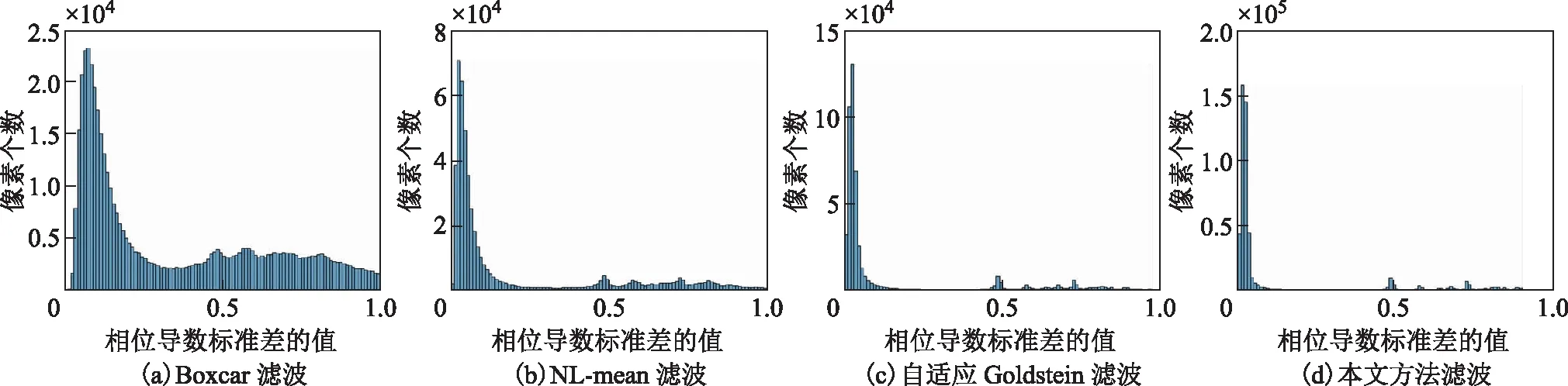
图8 4种滤波方法干涉结果的相位导数标准差统计图对比
4 结束语
本文将频谱细化原理与自适应滤波相结合,通过提升图像变换为频率域的频率分辨率的方式,更好地区分干涉相位中的噪声信息来提升滤波效果与滤波质量,在保证良好的去除噪声能力的同时又保证了条纹细节不被破坏。通过仿真实验与实测数据,用本文方法与Boxcar滤波、非局部均值滤波以及自适应Goldstein滤波方法作实验对比,在相位残差点数量和相位导数标准差中,本文的滤波方法相对于其他3种方法效果更好。在仿真实验误差分析中,本文滤波方法对数据滤波后的准确性较高,有利于提高干涉测量的精度。通过以上实验内容证明了本文滤波方法的有效性。

