基于虚拟同步的永磁风力电机组并网下频率调节研究

韩成春， 崔庆玉

(1.徐州工程学院 电气与控制工程学院，江苏 徐州 221018； 2.徐州工程学院 外国语学院，江苏 徐州 221018)

0 引 言

随着各国的经济发展，对能源的需求量也持续增加。风能具备含量高、无污染和可再生等众多优势获得了广泛应用。对风能进行开发的过程中，直驱永磁同步风力电机已获得众多学者的研究[1-4]。根据前期文献报道与相关试验分析可知，目前已经可以实现储能辅助调频、虚拟惯性控制、预留容量最大功率点跟踪(maximum power point tracking,MPPT)调控与虚拟同步电机调节等功能[5-6]。对预留容量进行MPPT控制的过程是以风力电机减载方式或增大桨距角的方式来实现[7-9]。相对于虚拟惯性条件下的控制方式，采用虚拟同步电机进行控制时可以在动态下获得自治频率信息，因此能够消除以锁相环进行电网测试所导致的频率检测不稳定问题[10]。还有学者[11]为VSG模型构建了传递函数，同时根据系统稳态与动态特征，优化了各项系统参数。由于VSG的虚拟参数可以实现灵活可调的功能，有研究人员在并网条件下，按照实际运行状况来达到自适应调节VSG算法虚拟转动惯量参数的功能，使系统获得更优动态响应性能。

考虑到VSG在孤岛运行状态下会发生频率偏移的情况，文献[12]调整了算法结构，同时结合同步电机的二次调频原理，在确保系统运行稳定的条件下，进一步优化控制参数来达到对系统频率的精确控制。

1 VSG控制策略

当负荷有功功率改变后，传统形式的同步电机由输入端获得的机械功率与输出端的电磁功率无法达到平衡的状态，从而引起电机输出频率的较大差异。图1为VSG控制策略结构图。

图1给出了直驱永磁风力发电系统电网侧变流器所使用的VSG控制策略，对同步电机功频与励磁特性进行了模拟分析。

采用式(1) 表示有功频率控制器同步电机二阶模型转子运动方程：

(1)

式中：J为电机转动惯量；δ为同步电机功角；ω为电机额定角速度；D为调整系数；Δω为电机额定与实际角速度差；Tm为电机输入机械转矩。Δω较小时，将上述转矩由式(2)表示。

图1 VSG控制策略结构图

(2)

式中:Pm为输入机械转矩；Te为输出电磁转矩；ωN为电机实际角速度；Pe为逆变器输出功率，取决于逆变器输出电压与电流。Pe通过式(3)进行计算。

Pe=uaia+ubib+ucic

(3)

式中：ua、ub、uc分别为逆变器输出三相电压；ia、ib、ic为逆变器输出三相电流。

2 VSG控制在并网下的稳定性分析

图2给出了VSG并网条件下形成的等效电路。并网条件下将其由式(4)表示。

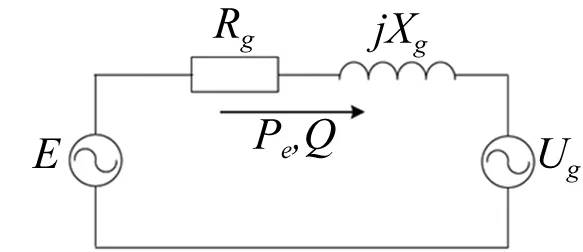
图2 逆变器在并网时 的等效电路图

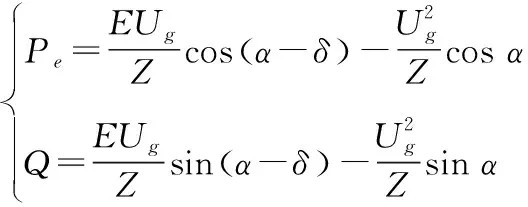
(4)

式中：E为逆变器输出电压；Ug为电网电压；δ为逆变器电压与电网电相角差；Z为阻抗；α为示阻抗角；Q为逆变器输出的无功功率。

从图3可以看到,并网条件下VSG在s域中形成的小信号模型。

忽略两个环路耦之间的合作用时，可以利用式(5)表示有功功率闭环传递函数。

(5)

式中：Xg为阻抗Z的虚部。

上述传递函数对应的特征方程如式(6)所示。

(6)

3 仿真验证

利用MATLAB/Simulink软件建立仿真模型，进行仿真测试时，在逆变器输出端配备变比为150/380的变压器作为负载与电网间的连接结构。表1为仿真过程得到的参数。

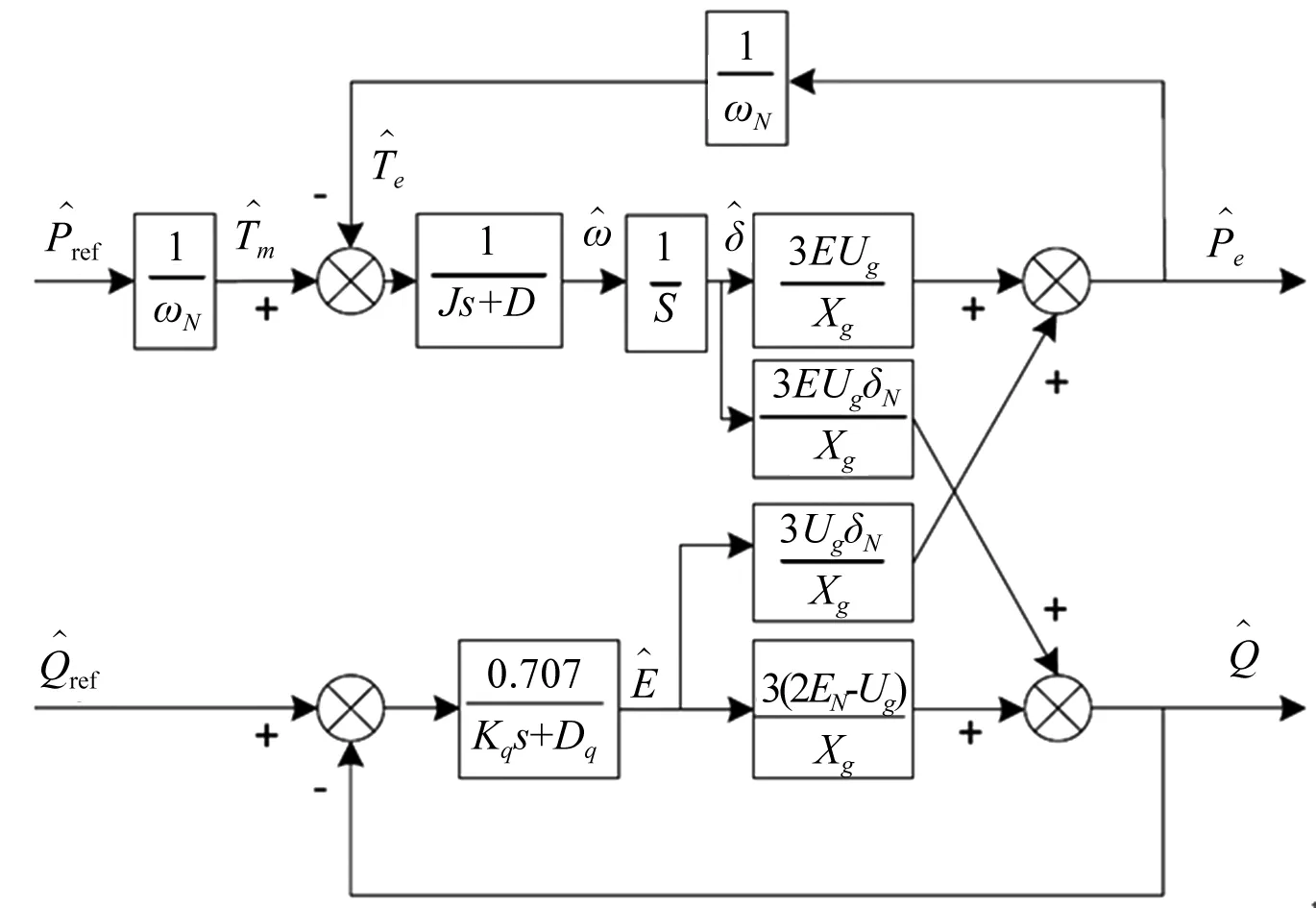
图3 并网下的小信号模型

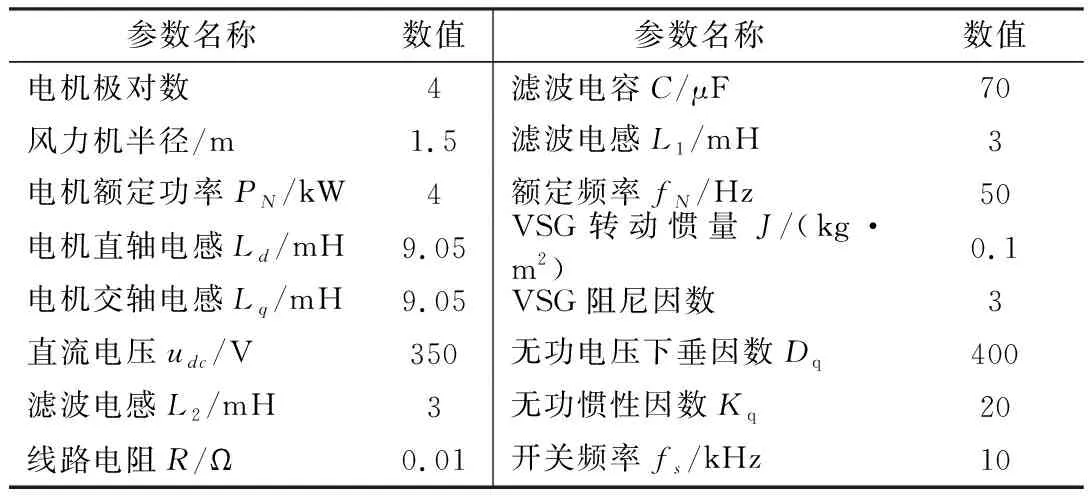
表1 仿真参数

分别对永磁同步电机进行q轴电流、d轴电流、电磁转矩以及直流母线电压进行测试，所得结果如图4所示。以id=0策略控制电机侧的变流器。根据图4(a)可知，d轴电流一直都为零；图4(b)与图4(c)分别为q轴电流与电机的电磁转矩波形，两者间呈现明显的比例变化特征；根据图4(d)发现直流母线电压与350 V设定值保持良好跟随性，获得了稳定的直流电压。

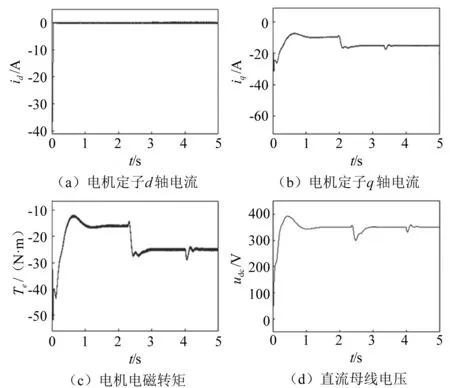
图4 并网下电机侧变流器控制变化量

图5(a)给出了下垂控制与VSG控制条件下随着有功负荷的增大形成的电机转速波形变化情况。图5(b)给出了并网下逆变器输出交流电形成的频率图。分析可知，频率也存在较大区别，电机转速发生了明显减小，可以释放转子动能来满足频率变化的需求。相对于同样条件下的下垂控制过程，采用VSG控制方式时电机转速发生了更明显的下降现象，因此能够更高效地满足频率变换要求。此控制方式下形成了更平滑的频率变化曲线，延长了调节时间，频率变化率显著减小，频率最低点也发生了提高，实现了频率的稳定变化状态和频率回归到额定值。

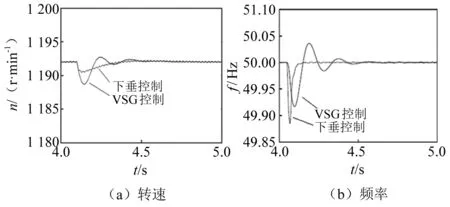
图5 并网下电机转速和逆变器频率波形

4 结束语

(1) 永磁同步电机q轴电流与电机的电磁转矩波形，两者间呈现明显的比例变化特征。直流母线电压与350 V设定值保持良好跟随性，获得了稳定的直流电压。

(2) 采用VSG控制方式时电机转速发生了更明显的下降现象，因此能够更高效地满足频率变换要求。此控制方式下形成了更平滑的频率变化曲线，延长了调节时间，频率变化率显著减小，实现了频率的稳定变化状态，频率回归到额定值。