基于OpenGL 的起伏地形条件下天然气管道路径优选

成毅 何晨 张岳

1中国石油国际勘探开发有限公司

2国家管网油气调控中心

我国的地理环境是西高东低，山地、高原和丘陵约占陆地面积的67%，盆地和平原约占陆地面积的33%，这就决定了在我国的油气管道项目中山区段的管道占有较大比重。受多种因素的制约，管道在山区管段的建设投资和运营代价要远高于平原地区的管道。因此，从2013 年开始，为了满足生产实际和降低成本以应对低迷油价的需要，部分学者开始研究三维地形条件下的管道路径优选问题。

周军针对气田管网，基于数字化地形数据，在考虑了各类环境因素以后，采用A*智能算法确定了气体管道最优路径，并将曲面路径的长度与路径投影为直线的长度进行了比较[1]。张思琦在三维地形条件下寻找最优路径时，将障碍、坡度等因素考虑在内，障碍区域的高程值转化成相对于整个区域较大的固定数值，从而使遗传算法的适应度函数值降低而在迭代的工程中被淘汰，进而达到了避开障碍的目的[2]。雷扬首先将障碍区域提取成凸多边形，然后采用模糊聚类分析把注水区域划分成多个子区域，最后利用智能算法确定了最优路径以及避障的距离[3]。

针对三维地形条件下的管道路径优选问题，国内外学者已经开展了大量的研究，并取得了丰硕的成果，但也存在一些难点和不足。三维地形的准确表征是解决三维地形条件下管道路径优选问题的前提[4]。现有研究主要采用三维曲面拼接的方式来表征地形，但是这种方式往往非常依赖曲面函数，鲁棒性不理想，而且模拟出的地形与实际地形误差较大（图1，图2）。因此，基于OpenGL 技术，使用空间插值方法建立DEM 模型从而进行三维地形表征，并采用D-P 算法进行路径优选。模拟实验结果表明，采用OpenGL 建立起的DEM 模型进行路径优选与用三维曲面建立的地形模型相比，前者误差更小，更加接近真实地形。D-P 算法可以有效地减少三维地形条件下管道长度，降低管道建设投资费用。

图1 三维地形条件下管道路径Fig.1 Pipeline path under 3D terrain condition

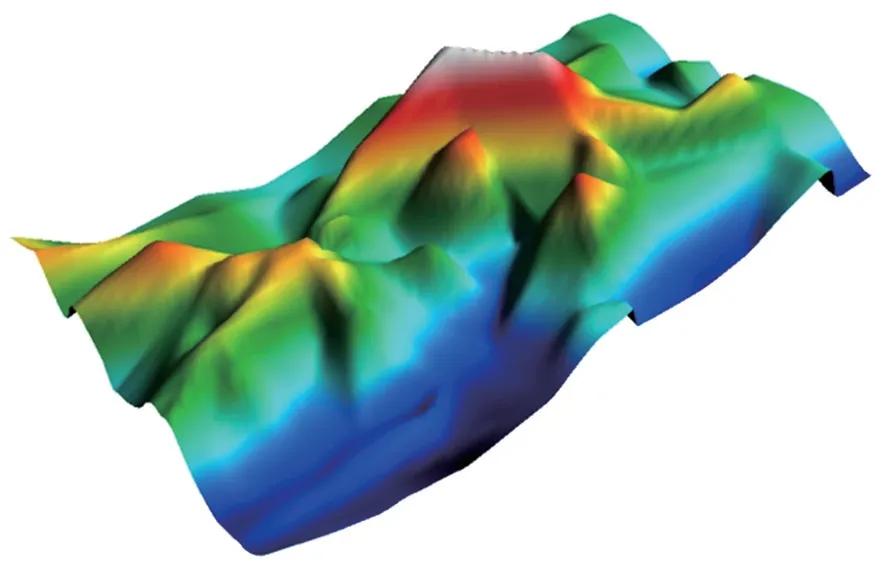
图2 真实三维地形图Fig.2 Real 3D topographic map

1 DEM 模型

DEM 是是当今地理学、气象学、计算机计算科学，尤其是地理信息科学研究的热点[5]。DEM 是表示某一区域地形D 上的三维向量有限序列，用函数的形式可以描述为

DEM 模型有两种表达形式：GRID 模型和TIN模型。TIN 模型在存储数据时，不仅要存储各个三角形顶点的高程信息，而且要存储三角形各个顶点的拓扑关系，因此数据结构复杂，效率较低[6]。另外，在构建三角网时需要用到较为复杂的算法，这更增加了建模的难度。GRID 模型在存储数据时，只需要存储网格点的起始坐标，网格行、列数以及各个网格节点的高程信息，因此，数据存储和读取方便，易于使用[7]。所以采用GRID 形式进行DEM模型建模（图3）。

图3 GRID 模型Fig.3 GRID model

1.1 GRID 模型建模步骤

在现实生活中，采样得到的数据往往是离散的随机分布的，因此需要将离散数据网格化。离散数据网格化的一般做法是：根据精度要求，对地形进行网格划分，然后再利用空间插值的方法计算出每一个网格节点的值，进而形成三维地形。GRID 模型建模流程如图4 所示。

图4 GRID 模型建模流程Fig.4 GRID model modeling process

1.2 GRID 模型数据存储结构

GRID 模型中需要存储的高程数据可以表示如公式（2）、（3）、（4）所示：

式中：X0、Y0为DEM 起始点横纵坐标；Dx、Dy为x方向和y方向上的间隔；Nx-1，Ny-1为DEM 网格的行列数。

可以看出，GRID 在存储数据时，只需要存储初始点坐标，网格的间距，网格点的高程以及行、列数就可以得到当前任何地形区域的高程信息。

2 模型建立

2.1 目标函数

建立三维地形条件模型的目的是使管道投资建设费用最少，这里的费用主要与管道的长度和管径有关。为了简化计算和更好的关注问题本身，假设管道的管径一定，则管道的投资建设费用只与管道的长度有关，因此，以管道总长度为目标函数，建立如下数学模型:

式中：L为管道长度，m；Xi，Yi，Zi为搜寻第i个网格时的高程数据，m。

2.2 约束条件

弹性敷设就是不使用弯头，而是利用管道自身的弹性逐渐改变管道的走向。由于其具有应力分布均匀，不存在过高的峰值应力以及不需设置固定墩，施工方便等优点，所以成为天然气管道在起伏地区铺设的重要方式。弹性敷设时，管道的曲率半径应该满足管道的强度要求，垂直面上弹性敷设管道的曲率半径还应该大于管道在自重作用下产生的挠度曲线的曲率半径，曲率半径可以按照式（6）计算。

式中：R为管道弹性弯曲曲率半径，m；α为管道的转角，(°)；D为钢管外径，cm。

3 求解算法

3.1 Dijkstra 算法

Dijkstra 算法是目前公认的效果较好的最短路径寻优算法[8]，它是典型的单源最短路径算法，其在现实世界中的应用非常广泛，例如在道路管网铺设中的运用，智能交通系统中的运用，管道铺设中的运用。它的基本思想是：对路径中可能经过的各个节点进行编号，然后遍历各个节点，计算出起点到终点可能经过的路径的距离，最后找出最短路径[9]。由于遍历了所有的节点，因此一定可以找到一条最短路径。图5 为一个无向带权联通图，利用Dijkstra 算法，可求出v0与v3的最短路径。

图5 无向带权联通图Fig.5 Undirected weighted connection graph

要从v0到达v3有5条路径：v0v3，v0v1v3，v0v1v2v3，v0v4v3，v0v5v4v3，这五条路径耗费的距离分别为5、10、15、3、6，由此可以看出从v0到达v3的最短路径为v0v4v3，距离为3。

从上述利用Dijkstra 算法求最短路径的过程可以看出，Dijkstra 算法不限制搜索方向，可见其搜索量巨大，时间复杂度较高；而且Dijkstra 算法采用的是邻接矩阵数据构，占用的内存较大，空间复杂度较高，这些都无疑会降低Dijkstra 算法的路径寻优效率。

3.2 人工势场法

1986 年，Khatib 提出了人工势场法，其基本思想是将机器人的规划空间看成一个受障碍物的斥力场和目标位置的引力场共同作用下的人工势场，在斥力场和引力场的共同作用下，移动机器人从高势点向低势点移动，最后完成路径寻优[10]。

人工势场分为两部分：①由目标位置产生的引力场，场强与机器人到目标点的距离成正比，即机器人到目标点的距离越大，场强越大；机器人到目标点的距离越小，场强越小。机器人的受力方向是由机器人指向目标点（Goal）[11]；②由障碍物产生的斥力场，场强与机器人到障碍物的距离成反比，即机器人到障碍物的距离越大，场强越小，机器人到障碍物的距离越小，场强越大，机器人的受力方向是由障碍物（Obstacle）指向机器人[12]。

机器人在人工势场中的受力如图6 所示。Obstacle 为障碍物，Start 为起点位置，Goal 为目标点位置，Frep 为障碍Obstacle 对机器人的斥力，Fatt为目标点对机器人的吸引力，Ftotal 为障碍和目标点对机器人的合力。由于在机器人寻找最短路径的过程中，其受到斥力和引力两方面因素影响，因此会被限制搜索方向，提高了搜索效率。

图6 人工势场法受力图Fig.6 Artificial potential field stress diagram

综上可得，Dijkstra 由于遍历了整个区域的节点，因此，其必然可以找到一条最短路径，但也正因此，在数据量巨大的情况下，其搜索效率较低[13]。人工势场法在搜索路径时，由于其受到斥力场和引力场两方面因素的影响，因此可以限制搜索方向，提高了搜索的效率[14]。基于Dijkstra 算法和人工势场法，提出了D-P 路径搜索算法。

3.3 D-P 搜索算法步骤

（1）三维地形的建立。根据精度要求，对地形进行网格划分，然后再利用反距离权重插值的方法计算出每一个网格节点的值，进而形成三维地形。树形结构在存储数据时具有独特的优势，它可以减少数据量，提高查找效率。因此，采用四叉树数据结构来存储网格的起始点坐标、网格间距以及各个网格交点的高程值信息。

（2）基准路径的建立。连接起点和目标点，形成一条基准路径。以合适的宽度将基准路径拓宽，形成一条基准路径带。

（3）地形复杂度的获取。地形复杂度是描述地形陡峭崎岖的重要指标，不同的地形因子刻画了不同的地形几何特征。常见的地形复杂度因子有局部高差、局部标准差、局部褶皱度、局部全曲率四种。局部高差即目标区域内最高点与最低点的高程值之差，它反映了目标区域内地形的起伏程度。局部标准差就是目标区域内高程的标准差，它反映的是目标区域内地形平均起伏程度。局部褶皱度是地形的三维面积与投影平面面积之比，它描述了地形的平均褶皱程度。局部全曲率反映的是目标地形的平均突变程度。利用人工势场法搜索最短路径，必须知道障碍区域的位置，因此采用局部全曲率来计算地形复杂度。

局部全曲率的表达式如式（7）所示。

式中：r为x方向的二阶偏导数；t为y方向的二阶偏导数；s为x，y方向上的偏导数。

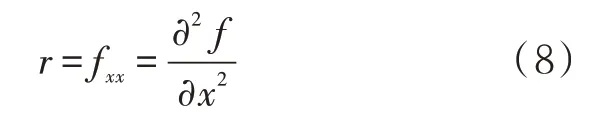
利用局部全曲率计算出地形复杂度后，与预先设定好的阈值进行比较，得出障碍的位置，障碍记为Obstacle。

（3）利用D-P 算法进行路径优选。首先利用人工势场法确定路径搜索的方向，设搜索点位置为X=(x，y，z)，引力势函数定义为

式中：Uatt为目标点的引力场；k大于0 的引力势场常量；X为搜索点的位置向量；Xg为搜索点在势力场中的目标点位置。

斥力场函数定义为

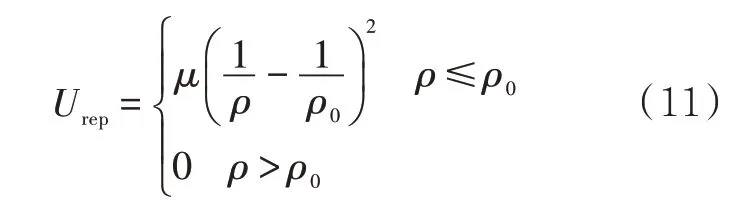
式中：Urep为障碍物的斥力场；μ为斥力场的常量；ρ为搜索点在空间位置与障碍物的最短距离；ρ0为单个障碍物影响的最大距离范围，当搜索点与障碍物的位置大于ρ0时，障碍物对于搜索点的运动不再产生影响。

在确定了搜索方向之后，利用Dijkstra 算法进行路径优选。

4 实例

4.1 地形模拟

在Google Earth 中以1 200 m×1 800 m 为范围随机提取2×104个点的高程数据，然后以10 m 为分辨率对该区域进行网格划分，最后利用反距离权重插值法计算出每一个网格节点的高程值，生成三维地形（图7）。管道起、终点坐标以及边界坐标见表1。

图7 OpenGL 建立的三维地形网格图Fig.7 3D terrain grid map established by OpenGL

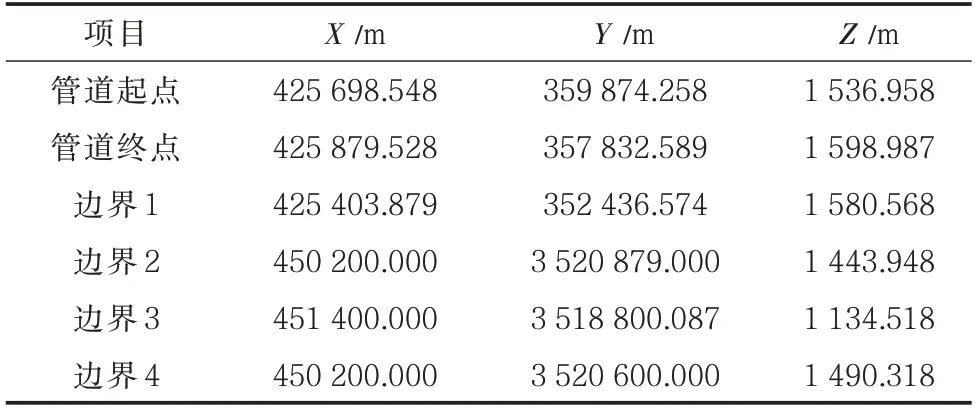
表1 管道起、终点坐标以及边界坐标Tab.1 Starting,ending,and boundary coordinates of the pipeline

从建立的DEM 模型中随机提取15 个点的高程数据，与从三维曲面生成的地形中提取的高程数据以及真实高程数据进行对比结果如表2。

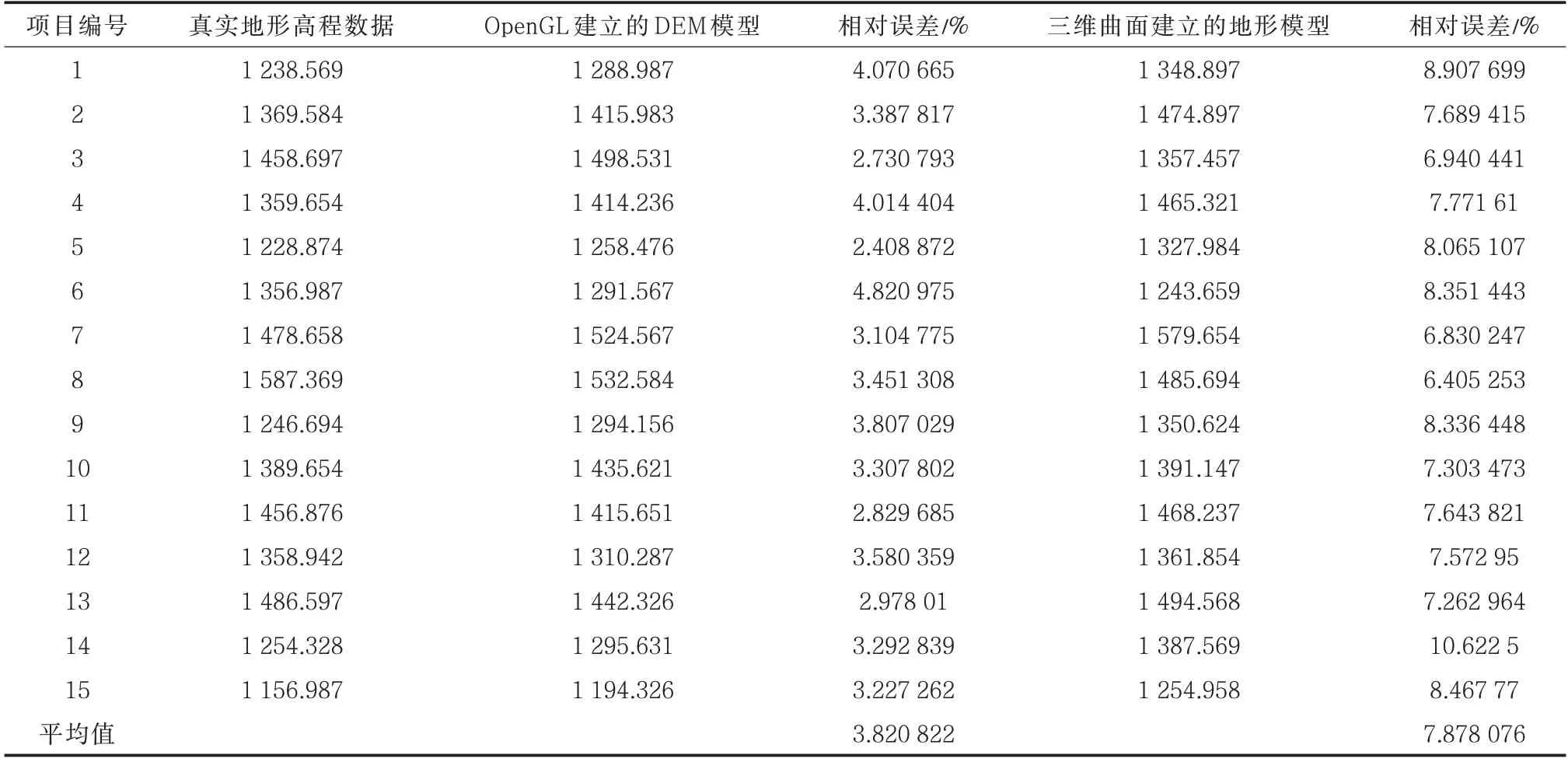
表2 高程数据及误差对比Tab.2 Elevation data and error comparison

高程数据对比结果如图8 所示，误差对比结果如图9 所示。从图8 和图9 可以看出，基于OpenGL建立的DEM 模型的高程数据与真实值的误差比采用三维曲面拼接建立起的地形模型的高程数据误差小，精度也更高。

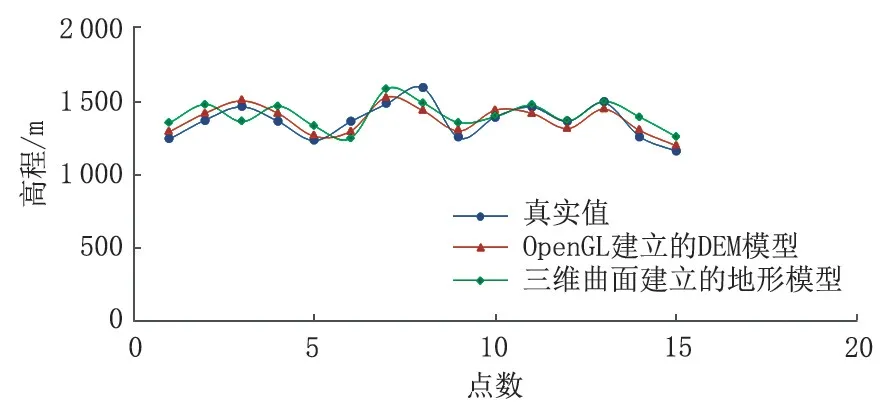
图8 高程数据对比Fig.8 Elevation data comparison

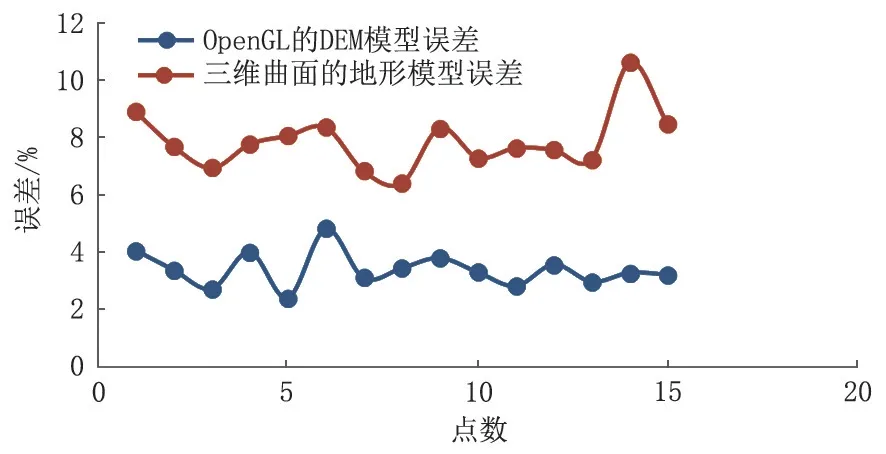
图9 误差对比Fig.9 Error comparison

4.2 路径优化

采用D-P 算法从管道的起点开始搜索，得到起伏地形条件下的天然气管道优化路径（图10）。

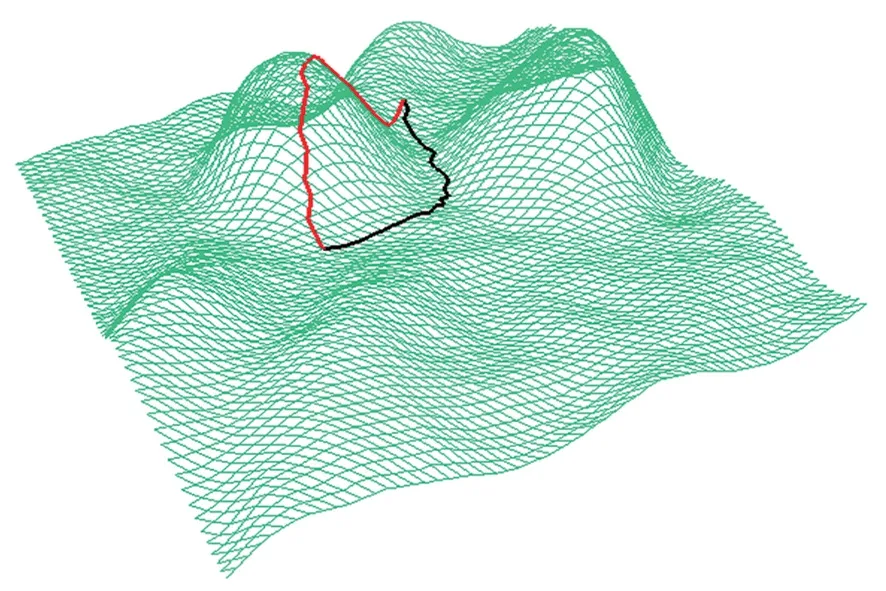
图10 地形起伏地区天然气管道优化路径与直线路径Fig.10 Optimal route and straight-line route of natural gas pipeline in undulating terrain

图10 中红色线代表管道直线路径，黑色线代表优化路径。计算得到起伏地形区域天然气管道的直线路径和优化路径的总长度如表3 所示。

表3 起伏地形区域直线路径长度和优化路径长度对比Tab.3 Comparison of straight path length and optimized path length in undulating terrain area

分析上述实验数据可以得到:

（1）优化后的路径在三维空间上的总长度比直线路径在三维空间上的总长度少208.4 m，优化率达到了10.6%。

（2）由图10 可以看出，优化后的路径避开了起伏较大的障碍区域，沿程的地形起伏更加平缓。

5 结论

（1）基于OpenGL 建立的DEM 模型和通过三维曲面拼接建立起的地形模型相比，前者模型的高程数据更加接近地形真实地形，误差更小，精度更高。

（2）基于Dijkstra算法和人工势场法提出的D-P算法不仅可以降低管道总长度，减少管道投资费用，而且还可以有效地降低管道沿线的地形起伏程度。