基于皮尔逊理论与径向基函数神经网络的光伏功率预测

李光华

（中移（杭州）信息技术有限公司）

0 引言

大规模光伏并网发电在解决能源问题上有着重要作用［1］，但光伏输出受太阳辐射强度、温度等各种因素影响，导致其输出具有时变性，给并网的控制调度带来较大的挑战。因此对功率的准确预测，可以有效提高电力系统并网运行的安全性和稳定性［2－3］。

目前光伏预测主要采用物理建模法和数学统计法对未来的光伏功率进行预测。物理建模法通过天气预报获取太阳辐照强度、太阳辐照时间以及云量等气象因素，结合光伏板实际的工作特性获得光伏输出数据［4］。数学统计法对历史数据进行分析，可以更好地映射输出功率与历史数据的关系。尤其随着现代化光伏电站的建设，历史发电及气象数据更多维，统计预测方式发展更迅速［5－8］。

文献［5］将太阳辐照作为输入建立线性回归算法，仅用太阳辐照强度一个输入量对光伏功率进行预测，使得预测精度不高。文献［6］用湿度和气温作为输入，采用自组织特征对天气类型进行聚类，分季节建立基于BPNN网络的短期功率预测，但只以两个参数作为输入，容易陷入局部最优问题。文献［7］以太阳辐照强度、温湿度、风速等作为预测输入，采用BPNN进行建模。该方案预测结果有一定提升，但是BPNN易陷入局部最小化误区。文献［8］采用相邻日的历史数据，用Elman神经网络进行建模。该方案在气象条件变化不大时预测精度较高。

本文提出以皮尔逊相关系数确定对光伏输出影响较大的气象因素，以最佳相似日和待预测日的气象因素作为输入，构建径向基函数神经网络对功率进行预测。RBF结构简单，学习收敛速度快，具有很强的逼近非线性函数能力。

1 皮尔逊相关系数法确定输入参数

本文的历史数据有：输出功率、风速、气温、相对湿度、水平面总辐照度、水平面散射辐照度。其中某些维度对输出影响较大，对这些因素进行关联度的分析，从而确定预测参数［10－11］。

本文用皮尔逊相关系数法，筛选出与光伏功率相关性较大的气象因子。0.8～1.0表示极强相关，0.6～0.8表示强相关，0.4～0.6表示中等程度相关，0.2～0.4表示弱相关，0.0～0.2表示极弱或无相关。式中，ρX，Y表示皮尔逊相关系数，X、Y分别气象因素和功率，N为样本数量。

为直观显示光伏输出功率与各气象因素的关系，图1以某日从8：00到18：00，展示输出功率与各气象因素的关系：为定性计算功率与各气象因素的相关性，本文采用皮尔逊相关系数法计算相关度。其计算结果如表1所示。为兼顾输入维度以及计算速度，本文选择相关度较高的前3个气象因素作为预测的输入。

图1 光伏功率与各气象因素关系图

表1 光伏功率与各气象因素的相关系数

2 相似日的选择

光伏系统输出功率受天气等自然条件的影响，在类似的气象条件下，光伏输出功率类似［12］。为提高光伏发电功率的预测精度，需从大量的历史数据中，筛选出与待预测日气象条件相似度较高的相似日作为预测的输入变量。每个输入向量可用如下表示：

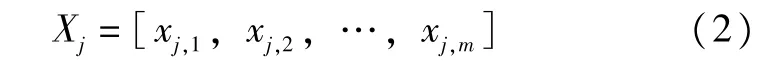
式中，Xj表示第j日的输入向量；xj，m表示第j日第m维输入数据。

由于各气象因素的量纲不同，并且数值范围也差多个数量级，便于后续数据的处理，需要对各个维度的输入数据进行归一化处理。归一化公式如下：

待预测日的气象数据可从气象部门获取，采用欧式距离法计算最佳相似日：

式中，Dj表示第j日与待预测日的欧式距离；表示第j日的第k维输入数据；x′k表示待预测日的第k维输入数据；m为输入向量的维数。

3 径向基神经网络

径向基函数神经网络是前向神经网络，于1988年提出，根据生物神经元具有局部相应的特点，将RBF引入神经网络中。RBFNN具有三层结构。第一层为输入层，由信号源节点组成。第二层为隐藏层，串联输入层和输出层，其变换函数是径向基函数，是对中心点径向对称且衰减的非负局部响应函数。第三层为输出层，用于对输入完成输出的变换，本文为输出的功率值。输出层是对线性权值进行调整，采用的是线性优化策略，因而学习速度较快［13］。

由于被控对象具有非线性、多变量特性，考虑到RBF能任意逼近非线性函数，在网络结构简单的条件下，有很好的泛化能力，因此本文选择用RBF作为预测模型，对光伏功率的输出进行预测。

4 实验数据及结果分析

本文的输入向量由最佳相似日的功率、水平面总辐照度、水平面散射辐照、日最高温度、日最低温度以及待预测日的日最高温度、日最低温度组成。输出向量由待预测日的输出功率组成。以某光伏发电站的公开数据，作为本次的实验数据进行预测模型的训练。

为考察训练获取的模型的预测能力，将其与BPNN进行比较。本文从每个季节中随机选择一日进行预测，其预测结果与实测功率见图2。

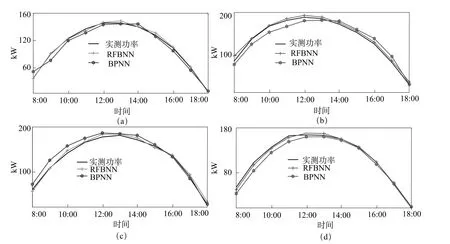
图2 功率预测与实测值关系图

为定量考察模型的预测能力，本文采用均方根误差eRMSE和平均绝对百分比误差eMAPE对预测结果进行分析，其计算方式如下：

式中，P′i为预测值；Pi为实测值；N为采集数目。

两种预测模型得到的误差值如表2所示，可以看出，使用RBFNN的相似日模型相较于BPNN，其eRMSE的BPNN均值从7.93降低到RBFNN的5.04，其eMAPE的BPNN的均值从18.26%降低到RBFNN的7.05%。

表2 预测误差比较

5 结束语

本文采用皮尔逊相关系数法，选择对输出功率影响较大的气象因素作为输入参数。再以这些输入参数，根据欧氏距离选择待预测日的最佳相似日，用RBF神经网络建模进行功率的预测，结果表明采用该方案的预测模型预测性能较佳，具有一定的实用价值。