基于新型液冷板的电池热管理系统多目标优化
张 林
(重庆交通大学机电与车辆工程学院,重庆 400074)
传统燃料汽车的尾气排放造成了严重的环境污染问题,影响人类的生存和发展。因此,新能源汽车的研究具有重要意义。锂离子电池技术是电动汽车的关键,通常锂离子电池最佳工作温度在20~40℃范围内,电池间温差小于5℃。锂离子电池长期处于高温工作环境会导致电池热失控,甚至发生爆炸。因此,需要设计一个高效的BTMS,来保障锂离子电池正常工作。
近年来,许多学者研究了不同换热介质下电池的散热性能, 主流的BTMS方法包括空冷、 液冷、 相变材料(PCM)冷却和热管冷却。液体冷却因其导热性好、冷却效率高、不易受环境温度影响而受到广泛关注。液体冷却可分为直接冷却和间接冷却。由于直接冷却要求冷却液绝缘且电池包具有良好的密封性,但这类绝缘的冷却液受其粘度的影响,在电池包内流动缓慢,因此热交换效率受到限制,故在实际应用中较少。对于间接冷却,目前最为常见的为液冷板散热冷却,而液冷板通道的结构设计成为了研究的重点,影响液冷板散热性能的因素有:通道进出口位置、管道布置形式 (蛇形、 “I”形、C形等)、通道相关因素 (包括数量、大小、间距等)以及冷却液相关因素(包括种类、流动方向等)等。通常在选定管道形式的基础上研究其他因素对散热效果的影响。如,Huo Yutao等在“I”形液冷板基础上研究了冷却通道数量、流量以及冷却液流动方向等因素对冷却性能的影响。结果表明通道数量越多,流量越大冷却性能越好,但数量以及流量增加到一定值后,冷却幅度降低,且考虑到经济性以及电池负载质量等,数量不超过5。L.W.Jin等提出了一种具有翅片结构的冷却板。结果表明,减小翅片密度或增大冷却液流量均可降低加热器表面温度。Jarrett A等采用蛇形通道,以平均温度、温度均匀性及压降作为目标函数,结合CFD方法,优化了通道宽度及位置。优化结果表明,系统的平均温度和压降得到了改善,但是温度均匀性变差。
而流动方向对散热性能的影响受管道布置位置所影响,文献[11]表明就其研究的散热模型而言,单向流动冷却性能优于双向流动,而文献[12]研究表明双向流动又优于单向流动。因此,针对不同的散热模型,流动方向对其散热效果也是不一致的。Liu Huaqiang等研究了通道内冷却液种类以及温度对散热性能的影响,发现散热性能与冷却液的比热容有关,向冷却液中添加微粒(AlO)有助于增加冷却液的散热性能。而Deng Yuanwang等则详细综述了典型的冷却液种类(水、乙二醇、油)以及向冷却液中增加不同纳米微粒添加剂以及含量对系统散热和压降的影响。
此外,BTMS是一个多目标优化问题,需要考虑各因素的综合影响。在Li W等的研究中,采用代理模型技术对液冷板冷却系统进行优化,以减小温差和压降。Liu Cheng等采用基于径向基函数的代理模型对BTMS设计变量进行多目标优化,优化了系统的散热性能。
传统的平行型和蛇形冷却通道存在较大的水力阻力和温度梯度等缺陷。在微电子器件中,分岔通道比平行直线通道和蛇形通道具有更好的散热性能。此外,它还具有低功耗的固有优势。基于此分析,基于树叶脉络形状,本文提出了一种新型的液冷板结构,以液冷板、和Δ为目标函数,利用NSGA-II对液冷板几何结构(通道角度、宽度)和冷却液质量流量等因素进行了多目标优化设计。最终在目标函数之间找到平衡点,该方法不仅提高了BTMS的散热效果,而且节省了计算成本。
1 模型介绍
1.1 单体电池实验
本文所用磷酸铁锂电池参数如表1所示。图1为实验平台,为得到模拟所需的电池产热参数,在25℃的恒温环境中,进行了单体电池充放电实验,得到电池的温升曲线。根据实验结果和文献[19]中对电池产热量的计算方法,如表2所示,计算得到了不同放电倍率下该款电池的产热参数。

图1 单体电池实验平台

表1 电池参数
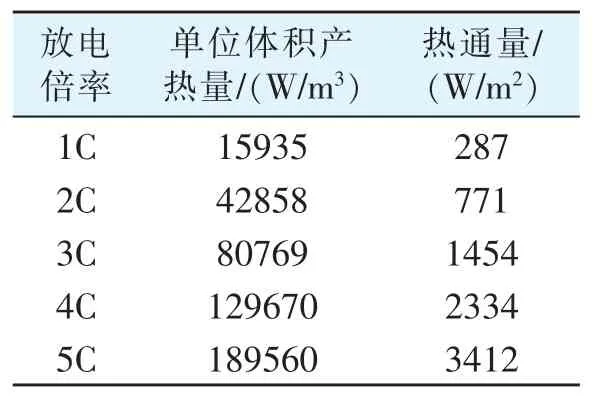
表2 不同放电倍率单体电池产热量
1.2 液冷板模型
图2 所示的自然界中树叶脉络,该形状有助于植物水分更好地向叶片的边缘运输。根据该特点,本文设计了如图2所示的液冷板模型,运用在液冷板中可以减小通道阻力减小压降。为了使该模型贴合电池,液冷板长×宽×高分别为140×65×3mm,冷却液通道为一进两出,内部通道高度=2mm,宽度=3mm。液冷板材料选用铝,冷却液选用水,具体参数如表3所示。热量传导方式如图3所示,电池均匀发热,热量由电池传递到液冷板再由冷却液对电池进行散热。在仿真计算时,将热量直接施加在液冷板上,以液冷板热性能代替电池热性能。
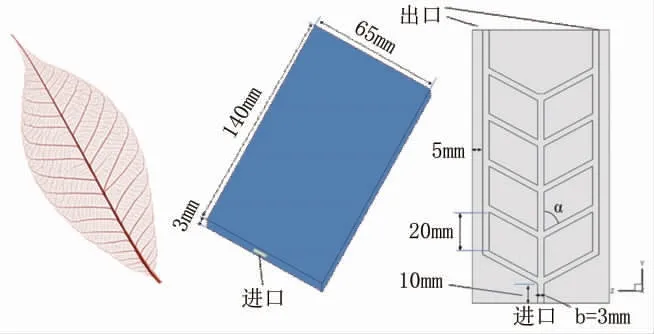
图2 液冷板结构
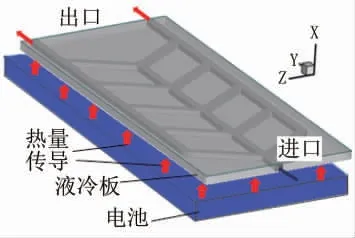
图3 液冷板散热示意图
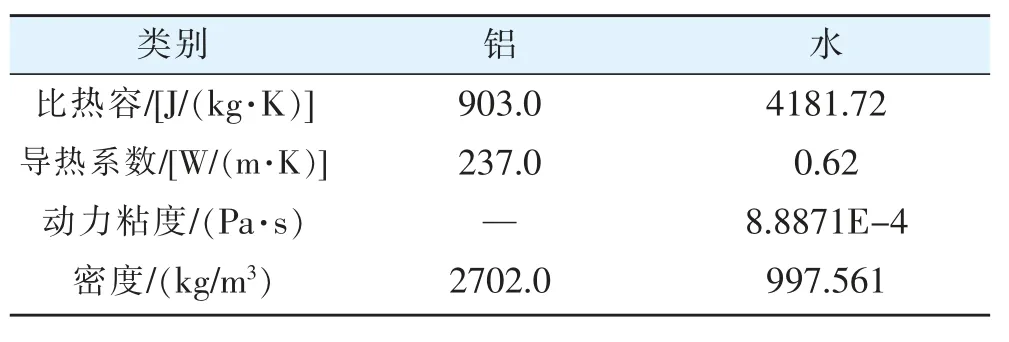
表3 铝和水的性质
1.3 数值解
边界条件
本研究采用Fluent软件进行稳态仿真。入口和出口分别定义为速度入口和压力出口。设置环境温度为25℃,初始流量为0.5g/s,本文中所讨论的冷却液质量流量的范围为0.2g/s到2g/s,这些工况的雷诺数都小于2300,所以在本文中的所有模拟工况均选择层流模型。以汽车爬坡或急加速等电池高倍率放电工况为背景,选择5C放电倍率。根据上文中所测的动力电池在5C放电倍率下的单位体积产热量189563W/m,转化为液冷板加热面的热通量为3412W/m。
为简化仿真,本研究在以下假设下进行:液冷板材质视为均匀的和各项同性的;冷却液为单相、不可压缩、稳态;水和铝的物理性质不受温度影响;忽略重力和粘性耗散的影响。
控制方程
基于上述假设,控制方程可以写成如下形式。
1)质量方程:

2)动量方程:

3)流体域的能量方程:

4)固体域的能量方程:

式中:ρ——冷却液的密度;——冷却液的速度;μ——冷却液的动力粘度;——冷却液的压力;——冷却液的比热容;λ——冷却液的导热系数。
网格独立性分析
本研究利用ICEM强大的结构网格对液冷板模型进行网格划分,结构性网格因其精度高、收敛速度快、更接近实际模型,被广泛应用于模拟中,图4为网格模型和局部放大展示图。网格数目对数值仿真结果也会造成影响,因此,需要对液冷板模型进行网格独立性分析。如图5所示,对比了6种不同网格数量下液冷板的平均温度和温度标准差结果。从图中可以看出,网格数量对模拟结果的影响不大,当网格数量为213832到1966900之间时,平均温度和温度标准差之间的差值都在0.1K以内。考虑到节省计算成本,本文选择的网格数为213832,接下来所有仿真都在此网格尺寸下进行。

图4 液冷板网格和局部放大图
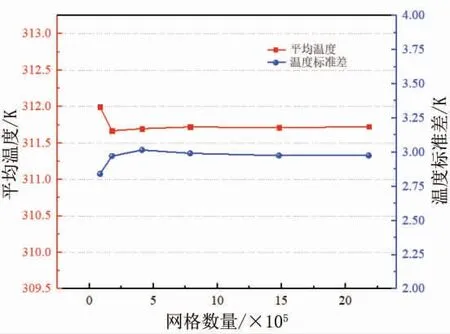
图5 不同网格数下的仿真结果
2 优化技术
2.1 设计变量和目标函数
由于通道夹角的变化会引起液冷板左右通道流量的改变从而影响冷板的均温性和压降,液冷板通道宽度会改变整个冷却通道的面积,增加冷却液流量可以有效降低液冷板的平均温度和温度标准差,但是系统的压降会随之增大,从而需要更大功率的冷却液泵来支撑,大大增加了冷却系统对电池能量的消耗,所以经过综合考虑,认为冷却液流量范围为0.2g/s至2g/s之间。综上,如图2所示,本文选择通道夹角α,通道宽度b,冷却液的质量流量m作为设计变量,考虑到液冷板尺寸和BTMS能耗等因素的限制,各设计变量的取值范围如表4所示。
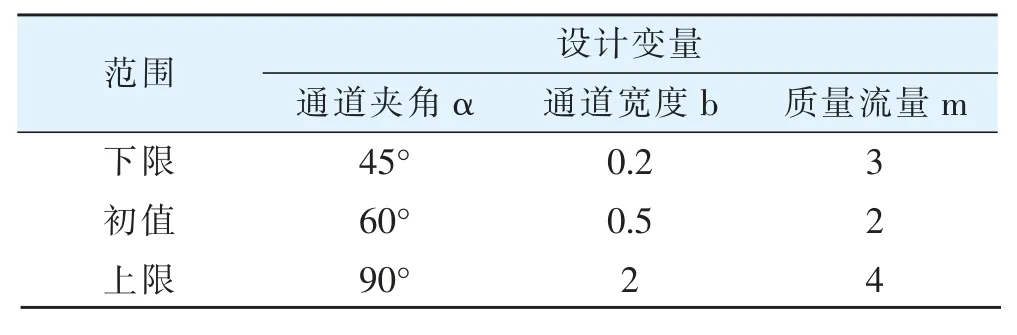
表4 设计变量的取值范围
本文选择液冷板的平均温度、温度标准差和压降作为目标函数。其中,液冷板表面平均温度可以反映系统的整体冷却性能;入口和出口之间的压降可以代表系统在冷却液上工作所消耗的能耗;温度标准差可以反映液冷板表面温度分布的均匀性。
2.2 优化流程及实验设计
采用NSGA-II对液冷板结构进行多目标优化。NSGA-II是一种以多因素为目标函数的综合优化方法,具有复杂程度低、所求解集的收敛性好、计算速度较快等优点。多目标优化过程如图6所示。
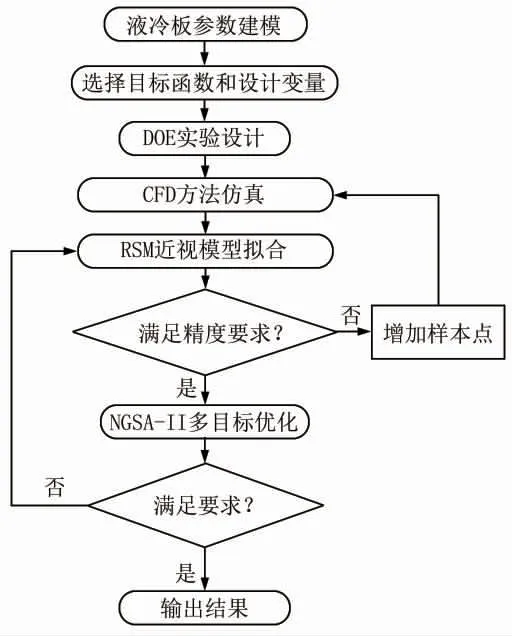
图6 多目标优化流程图
上述问题的多目标优化可表示为:
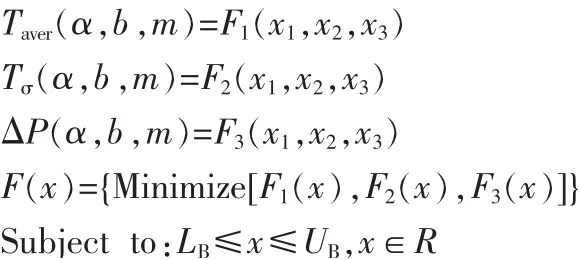
2.3 建立响应面模型
多目标优化设计需要对目标函数进行反复评价。近视模型以其迭代计算简单、计算周期短、结果误差稳定、不会降低模型精度等优点,在许多学科的优化设计中得到了广泛的应用。响应面模型(RSM)具有计算简单、所需实验数据少、计算精确等优点。因此,本文选择RSM来拟合设计变量和目标函数的函数关系式。
由于参数点的选取是创建代理模型的基础,所以参数抽样点要尽可能地保证其在抽样范围内的均匀性,以保证后续所生成代理模型的可靠性。采用最优拉丁超立方抽样(LHS)方法,根据各设计变量的取值范围,如图7所示,在设计空间选择了35个设计点。
所得到的抽样点在抽样空间内的布置情况如图7所示。通过分析图7可以看出,最优拉丁超立方生成的抽样点具有良好的随机性和均匀性。所以认为生成的抽样矩阵在抽样空间内也具有良好的均匀性与随机性。

图7 最优拉丁超立方空间样本点
利用CFD方法对抽样样本点进行模拟得到实验数据,模拟结果整理如表5所示。

表5 DOE实验数据
为提高拟合精度,采用四次方的响应面模型来逼近目标函数,术语选择采用两次替换法。RSM的误差分析如图8所示,在我们的研究中,平均温度、温度标准差和压降的多元回归系数()值分别为0.98062、0.98051、0.97431,均大于0.9,说明该近视模型能够准确代替该多目标优化。

图8 目标函数多元回归系数精度
2.4 优化结果
采用NSGA-II进行多目标优化,图9为各目标函数的历史迭代图。对于工程应用,可以根据实际需要进行定量分析,从结果中选择满足目标函数的最优解:α=48.211,b=3.937,m=0.8295。为了验证目标函数的可靠性,采用CFD方法对最优解进行了数值模拟。计算结果与仿真结果的关系如表6所示。

图9 目标函数历史迭代图
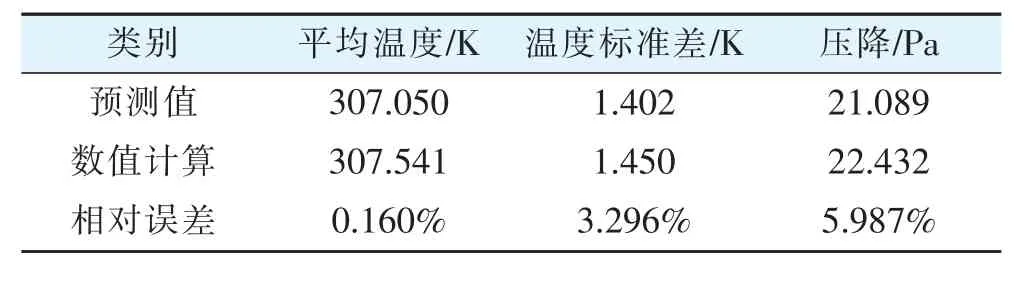
表6 计算结果对比
由表6可知,平均温度、温度标准差和压降的最大相对误差分别为0.16%、3.3%、5.99%,因此,可以证明优化结果的可靠性满足要求,目标函数能够较准确地反映液冷板的热性能。相比较于初始工况,液冷板平均温度和温度标准差分别下降了4.13K(11%)、1.52K(51.2%),压降仅增加了3.3Pa。
3 结果分析与讨论
3.1 温度场分析
比较优化前后液冷板温度分布的情况。如图10所示,可以看出:在液冷板进口与出口间形成了几个温度梯度,这是由于在这个过程中冷却液的温度上升,换热能力逐渐下降导致的。与优化前相比优化后液冷板的出口温度下降了8K,同时优化前液冷板的进出口温差为10K,优化后温差为5.5K,下降了4.5K。结果表明,优化后的液冷板的冷却效果有了明显改善。

图10 优化前后温度云图
3.2 速度流场及压降分析
优化前后液冷板的流速和压降情况如图11所示,可以看出优化后的冷却液流速大于初始工况,在相同冷却时间内可以带走更多的热量。同时,优化后的液冷板左右两个通道的流速大于初始工况,这有助于带走液冷板两边的热量,提高系统的温度均匀性。由于流速的增加,以此为代价导致了液冷板优化后压力损失增加。

图11 优化前后速度和压力云图
4 结论
为改善BTMS冷却效果,基于树叶脉络的形状,本文提出了一种新型的液冷板模型,研究了液冷通道结构对液冷板散热效果的影响。首先,搭建实验平台,得到了单体电池不同放电倍率下的发热量,建立传热模型。然后结合遗传算法对液冷板的通道宽度、通道夹角和冷却液流量进行了多目标优化,得到结论如下。
1)液冷通道的结构参数对液冷板散热效果有很大影响,合理地改变液冷通道结构,有助于提高BTMS冷却效率。
2)液冷板多目标优化最优解为:通道夹角为48.211°,通道宽度为3.937mm,质量流量为0.8295g/s。相比较于初始工况,液冷板的平均温度和温度标准差分别下降了4.13K(11%)、1.52K(51.2%),压降仅增加了3.3Pa。
3)与CFD模拟结果相比,多目标优化预测的液冷板平均温度、温度标准差和压降最大相对误差分别为0.16%、3.3%、5.99%,结果表明多目标遗传算法的预测精度较高。

