复合式置换法压井参数计算研究
张杰,杜肖潇,李鑫,李翠楠,王谣,漆琪,李荣鑫
(1.西南石油大学油气藏地质及开发工程国家重点实验室,成都 610500;2.西南石油大学石油与天然气工程学院,成都 610500;3.中国石油西南油气田分公司工程技术研究院,广汉 618300)
随着油气勘探开发领域逐步向深部以及超深部地层延伸,地层情况越发复杂,面对的高压油气层也越来越多,因此井控问题也越发突出[1]。若井内液柱压力在钻完井过程中与地层压力失去平衡,容易发生井下安全事故,不仅会对财产及现场人员安全形成严重威胁,甚至会对油气资源造成无法挽回的损失。面对日益复杂的井控问题,一般现场采用的较为常规的压井方法已经难以满足现场要求,因此非常规压井方法需求越发迫切[2-3]。
当发生溢流或井喷事故且现场不具备常规压井条件时,一般会采用较为特殊的非常规压井措施。置换法压井运用条件是当气井井喷导致井内液体被喷空后,井内只存在少量钻具或井筒完全处于空井状态,井内压井液无法建立循环,但压井液可经过节流压井管汇泵入井内从而达到井控目的。该方法是在关井前提下,明确井口套压上下限值,分次向井内注入一定体积的压井液再分次通过节流阀释放出气体逐步降低套压达到压井目的[4-6]。Mathews等[7]在20世纪80年代首次在浅井上运用置换法压井进行试验分析,并对置换法压井适用情况和相关压井案例进行了讨论和说明。Grace等[8]推导出了置换法压井过程中井口套压以及注入压井液量的理论计算公式,并初步提出了关于置换法现场简要施工方法的操作步骤。李运辉等[9]将置换法压井运用到川东北某异常高温高压气井井控问题处理上,并对压回法压井和置换法压井适用条件进行了分析。Yuan等[10]根据置换法压井步骤分析了操作方法原理和压井计算模型。任美鹏等[11]提出了动态置换压井法即不再在压井过程中先后向井内泵入压井液和通过节流阀排出气体,并建立压井参数计算模型,得到了最大压井液泵入速度和井口套管压力的变化规律,其研究结果表明动态置换法压井在小排量泵入压井液条件下能明显提高压井效率,且压井过程中井口套压较低能有效保障压井安全,因此可以用于指导现场压井作业。吕选鹏等[12]通过某井实际分析,提出了置换法运用过程中压井液类型、现场压井设备等其他相关设施的选用考虑因素。刘文远等[13]提出了自动化置换法压井技术,并考虑了压井泵排量、初始关井套压、钻井液密度等影响因素分析。Syarafi等[14]在节点分析稳态预测模型基础上,建立井喷时的动态模型,可为后续的动态压井提供可行性分析。Elgassier[15]考虑了置换压井过程中气体偏差系数的变化影响情况,计算了压井液泵入体积、排气体积以及井底压力变换值,但忽略了井筒压力变化规律。于晓东等[16]通过实验方法研究了置换法压井期间的压井液沉降规律,改善了Elgassier模型,并由此得到置换法压井过程井筒压力变化规律。毛良杰等[17]在天然气井溢流分析中考虑了H2S受温度和压力影响产生相态变化,对后期压井作业具有重要指导作用。王宁等[18]基于多相流模拟软件,将置换法压井模拟运用在深水井中,并成功实现深水井置换法压井自动控制。
但是在现场压井施工中,由于排气时间判断不准可能会导致操作人员提前打开节流阀进行排气,压井液由于液泛影响可能会随气体向井口移动等情况导致压井失败,以上研究缺乏在此条件下气体排放流量以及最佳排气速度、压井液泵入量、等待压井液下降时间等参数相关计算描述,且在现有研究中以上参数大多只是笼统计算或者没有涉及说明,静/动态置换压井法转换问题目前也还没有相应研究。为此,提出了复合式置换压井法即压井前期采用静态置换法压井并在合适时间段将压井方法转变为动态置换法压井,建立相应压井计算模型,并对气体排放流量、压井液最大泵入量、压井套管压力等参数进行计算与对比分析。对于完善井控理论,更加安全、高效、经济钻采油气藏具有重要意义。
1 复合式置换法压井计算模型
1.1 假设条件
基于井内全部充满气体且井内压井液循环无法建立的工况下建立复合式置换法压井各阶段计算模型。提出以下假设条件:气体排出过程排气速度可控;气体排出过程遵循质量守恒方程;气体排出过程气液满足泛流理论;考虑气体排出过程中密度变化影响;忽略气体在体积变化过程中产生的摩擦损失;整个过程不考虑温度影响和液体压缩。
1.2 静态置换法压井参数计算
运用置换法进行压井作业时,需要等压井液下降到一定深度后开始进行排气降压。在排气阶段,为了缩短压井时间会适当增大排气速度,但由于液泛影响,当排气流速增大到一定值后,部分下降的压井液受到向上运动气流的影响会改变流动方向,液体随气体向上流动。
基于圆球形液滴模型,分析液滴在井筒内随气体向上移动的运动状态:初始为加速运动,加速到一定数值后,液滴将做匀速运动,若在液滴即将到达井口时排气停止,在惯性力作用下,液滴将会继续向井口运动并对井口设备进行撞击,严重情况下可能会对井口装置造成损害。因此需要合理设计一段液滴到井口的安全缓冲距离L使液滴到达井口装置时速度降为0。其液滴在井筒内移动示意图如图1所示。
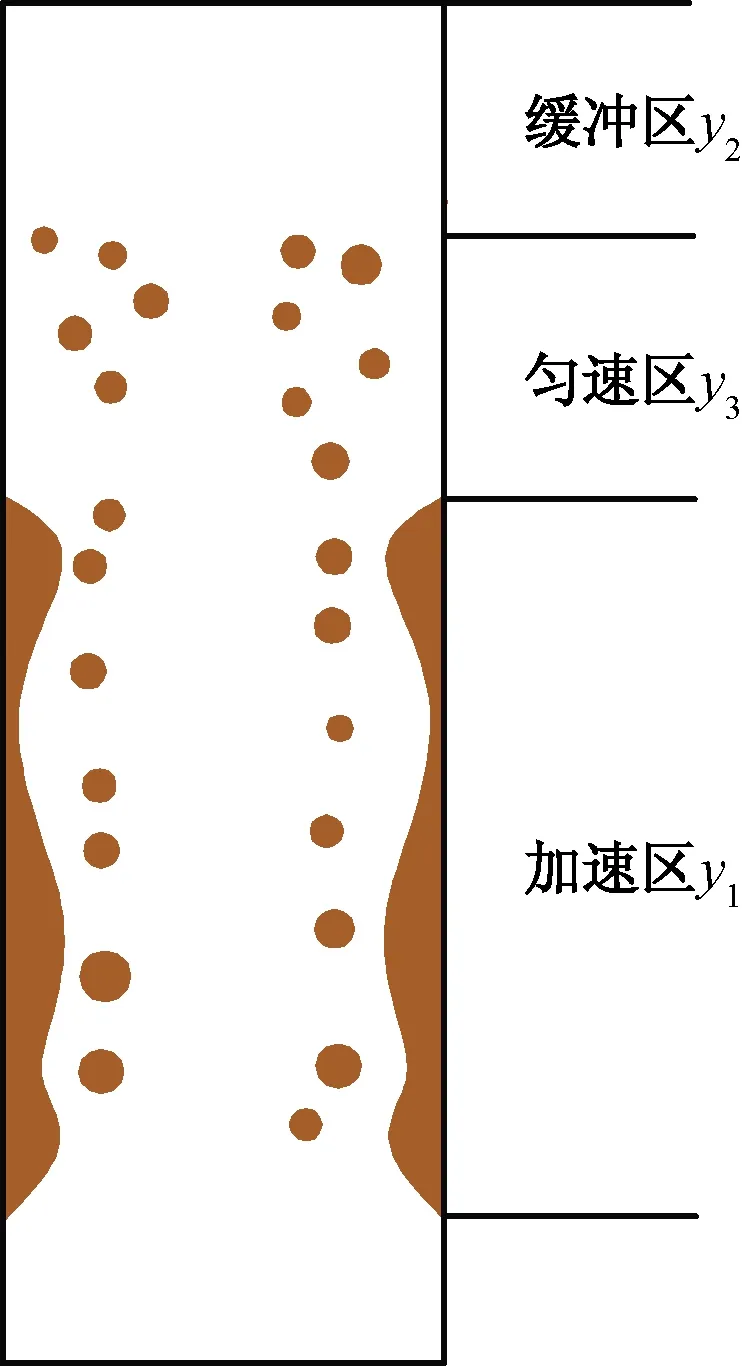
图1 液滴移动示意图
1.2.1 加速区参数计算模型
假设排气流量为Q,且满足液滴能被气体携带出井筒的条件,此时排气流速uq为
(1)
式(1)中:A为井筒截面积,m2。
在排气过程中,假设液滴流速为ut,则在t时刻,液滴相对于气体的速度urt可表示为
(2)
在关井时液滴可看作处于静止状态的条件下,液滴主要受到气体对其的拖曳力FD、浮力FB和自身重力FG。在开始排气的初始时刻,液滴在井内处于匀速运动状态,根据受力分析、式(1)、式(2),当液滴以最小直径稳定存在时[19],液滴的初始速度u0(定义速度方向向上为正)表达式为
(3)
式(3)中:σ为气-液两相表面张力,N/m;CD为拖曳力系数;ρk、ρg分别为液滴、气体密度,kg/m3。
随着排气的开始,液滴的运动状态由减速运动到速度变为0后逐渐过渡到加速运动,其液滴的加速度计算公式为
(4)
式(4)中:DP为液滴直径,m;u为液滴速度,m/s;g为重力加速度,9.8 s/m2。
此时液滴的相对速度u1和运动速度uc的表达式分别为
(5)
(6)
式中:u1、uc分别为加速阶段液滴相对速度、运动速度,m/s。
液滴速度从u0增加到u1所需时间t1为
(7)
因此,在t1时刻内液滴上升距离y1为
(8)
式中:t1为加速时间,s;y1为液滴加速上升距离,m。
1.2.2 缓冲区参数计算模型
当停止排气时,在惯性力作用下,液滴将会继续向井口设备做减速运动,此时液滴的加速度计算式为
(9)
当液滴速度从uc降为0时所需的时间t2为
(10)
因此,在t2时间内,液滴向井口运动的安全缓冲距离y2为
(11)
式中:t2为减速时间,s;y2为安全缓冲距离,m。
1.2.3 匀速区参数计算模型
关井时,液滴从井口下沉距离为L,排气过程中,液滴加速上升距离为y1,安全缓冲距离为y2,因此液滴以速度uc进行匀速运动的距离y3和时间t3为
y3=L-y1-y2
(12)
(13)
式中:L为液滴总下降距离,m;y3为匀速运动距离,m;t3为匀速运动时间,s。
1.3 动态置换法压井参数计算
根据所建立的工艺,在压井施工后期,在合适时间内将静态置换法转变为动态置换法进行压井,更大程度上排尽井筒内气体,且提高压井效率、节约压井时间[11]。此时,考虑气体排出过程中密度变化影响,因此优化后计算模型为
(14)
式(14)中:Qk、Qg分别为压井液泵入排量和气体排出流量,m3/s;Zt、Z0分别为t时刻和初始时刻井筒内气体的压缩因子,无量纲;Tt、T0分别为t时刻和初始时刻井筒内气体的温度,K;Pa0为采用动态置换法压井时关井套压,MPa;Vg为采用动态置换法压井时井内气体体积,m3;JG、JL分别为无因次气相速度和液相速度。
通过对式(14)求解,可得
(15)
式(15)中:D为井筒直径,m。
2 复合式置换法压井计算参数确定
2.1 置换法压井排气流量及参数确定
2.1.1 压井液随气体运动时间及距离的计算
根据加速时间计算可知,液滴能快速完成加速运动,因此在排气过程中,可忽略加速阶段的加速度影响,可用匀速阶段的速度代替加速阶段速度对压井液运动距离进行计算和求解。
第i次排气时间ti为
(16)
第i次排气液滴匀速运动速度uc(i)为
(17)
第i次排气阶段液滴在井内运动距离yi为
yi=uc(i)ti
(18)
则第i次排气前压井液在井内下降距离Li为
Li=yi+Δy
(19)
式中:VN(i)为第i次最大排气量,m3;Qi为第i次排气流量,m3/s;PM1为第一次向井内泵入最大体积压井液后井内气体的压力,MPa;Pa(i)为第i次排气后套压,MPa;VM(i)为第i次排气前气体体积,m3;uc(i)为第i次排气液滴匀速运动速度,m/s;Δy为停止排气液滴缓冲距离,m。
2.1.2 等待压井液下降时间的计算
由于压井液膜下沉速度小于液滴下降时速度,因此采用液膜下沉速度计算等待压井液下降时间。为尽可能保障压井液能全部下沉即排气阶段压井液不以液滴形式随气体向井口运移,应根据具体情况对等待压井液下降时间适当进行补偿。
第i次关井等待压井液下降时间t1(i)为
(20)
(21)
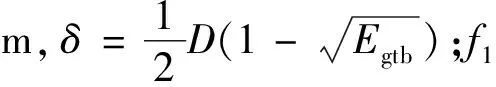
2.1.3 排气阶段气体流量的计算
排气阶段气体流量的控制方程为
(22)
式(22)中:Lgi为第i次泵入压井液前井内气体长度,m。
2.2 动态置换法压井参数的确定
采用动态置换法压井时,最大压井液泵入速度um的计算公式为
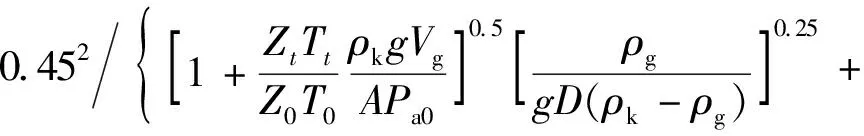
(23)
压井液最大泵入流量Qm为
Qm=Aum
(24)
气体排出最大流量Qg为
(25)
根据式(24)、式(25),设定压井液密度为1.2 g/cm3,套压分别为1、5、10、25、40 MPa,所得到的压井液最大泵入排量变化趋势如图2所示。
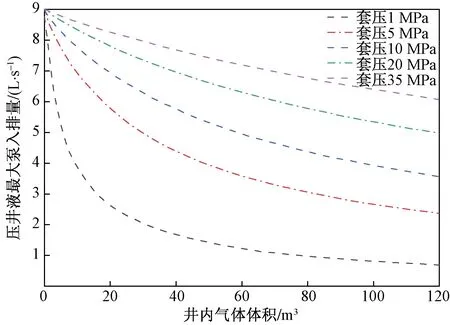
图2 不同套压压井液排量变化规律
设定套压为5 MPa,压井液密度分别为1、1.25、1.5、1.75、2 g/cm3,所得到的压井液最大泵入排量变化趋势如图3所示。
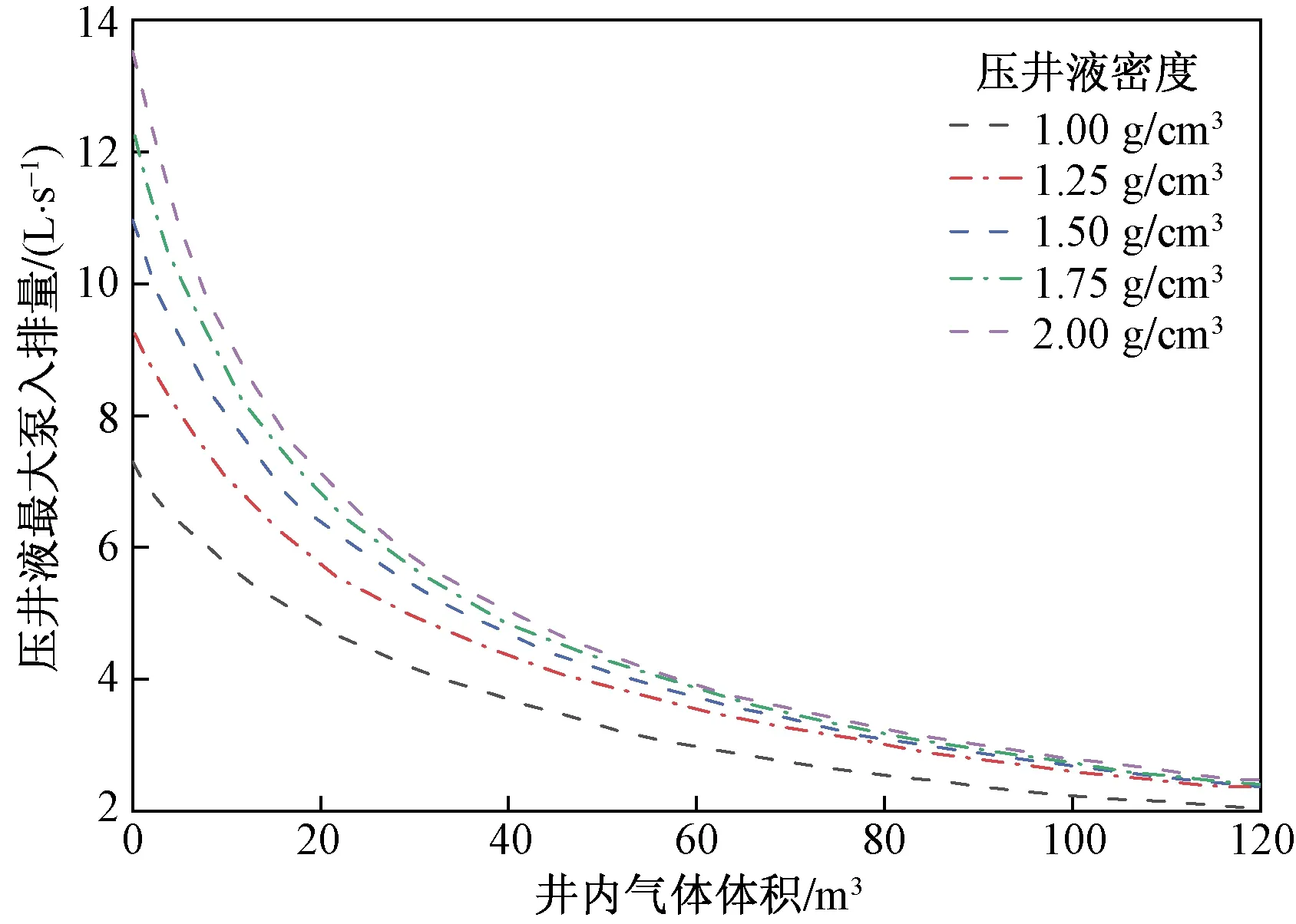
图3 不同压井液密度下压井液排量变化规律
从图2可得,压井液密度不变,若压井套压越大,则压井液最大泵入量亦会越大;随着井口套管压力增加,当井内气体体积在20 m3以内时,其变化幅度明显变小;若井内气体体积越大,井口套管压力的影响力也会逐渐增大,压井液最大泵入排量相差变得明显。从图3可得,套管压力不变,若此时压井液密度愈大,则其最大泵入量亦会愈大,且随着压井液密度增加,压井液最大泵入排量增大幅度变小,随着井内气体体积增加,压井液密度的影响力渐弱,压井液最大泵入排量值接近。
静态置换法压井在第i阶段泵入压井液体积为Vi,采用动态置换法压井泵入相同体积需要时间tD(i)为
(26)
根据所建立的压井工艺,需在合适时间内进行静/动态置换法压井工艺转换,因此,静/动态置换法压井工艺转换控制方程为
tD(i)≤f(Qi)+fL(QLi)
(27)
(28)
式中:Vi为第i阶段泵入压井液体积,m3;tD(i)为泵入相同体积需要时间,s;fL(QLi)为静态置换法压井第i次泵入压井液所需时间,s;QLi为静态置换法压井第i次泵入压井液排量,m3/s。
当计算结果满足上式时,在第i阶段时,压井方法由静态置换法压井转变为动态置换法压井。
2.3 复合式置换法压井套压计算
对于置换法压井,将每泵入一次压井液、等待压井液下降、排气降压、关井这一段过程称为一个阶段,用时间tAi表示,泵入压井液时间为tBi,等待压井液下降时间为tWi,排气时间为tPi。
(29)
(30)
(31)
tAi=tBi+tWi+tPi+tA(i-1)
(32)
对于第i阶段结束时的套压为
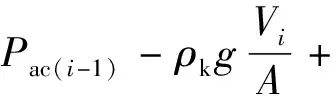
(33)
(34)
(35)
式中:VNi为第i阶段最大排气体积,m3;PG1,PGi分别为第1次和第i次排气前井内气体自重产生的压力,MPa。
假设在第n阶段换用动态置换法压井,则采用动态置换法压井时的套压随时间变化的关系式为
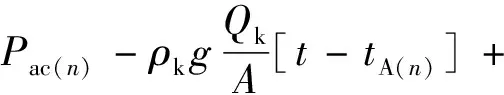
(36)
式中:tA(n)为第n阶段采用动态置换法后完成一个阶段所需时间,s。
2.4 复合式置换法压井泵入量计算
假设在第n阶段换用动态置换法压井,则采用动态置换法压井时的压井液泵入量随时间变化的关系式为
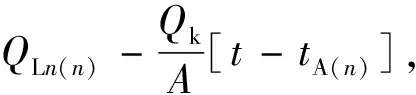
(37)
3 实例分析
3.1 计算结果
某井用直径215.9 mm钻头钻至井深3 000 m处时发生溢流,外径为244.5 mm(内径222.4 mm)套管下深2 785.30 m,裸眼段长214.7 m,地层压力为35 MPa,井内无钻具并充满气体。气体密度为0.6 g/cm3,关井套压为17.4 MPa,考虑压井液含气附加压力1 MPa,压井液密度为1.23 g/cm3。
分别以10 L/s,30 L/s的泵入速度向井内泵入压井液,根据以上相关计算模型和求解方法可知压井套压和压井液泵入量随压井时间变化趋势如图4、图5所示。
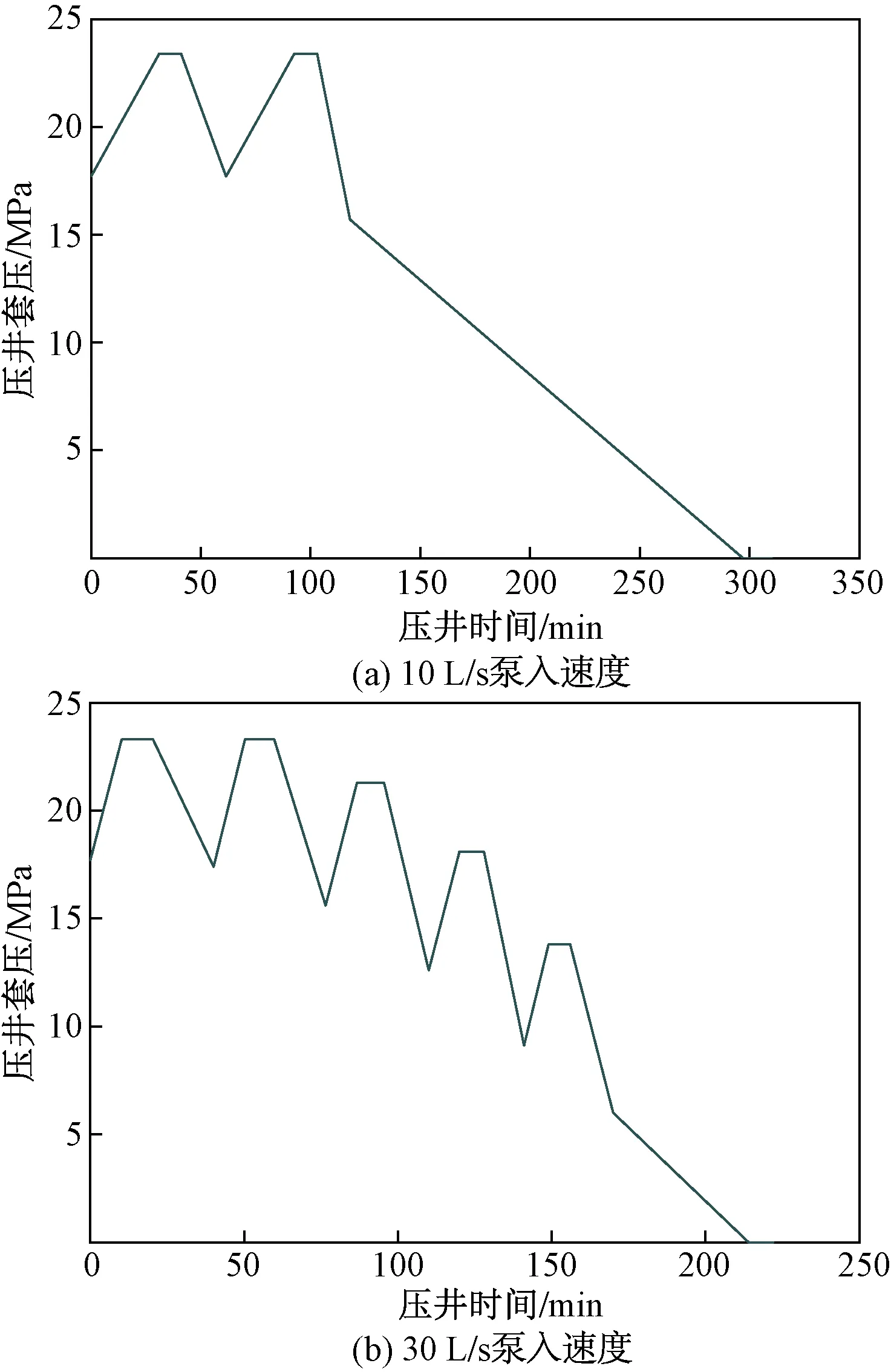
图4 不同泵入速度下套压变化规律
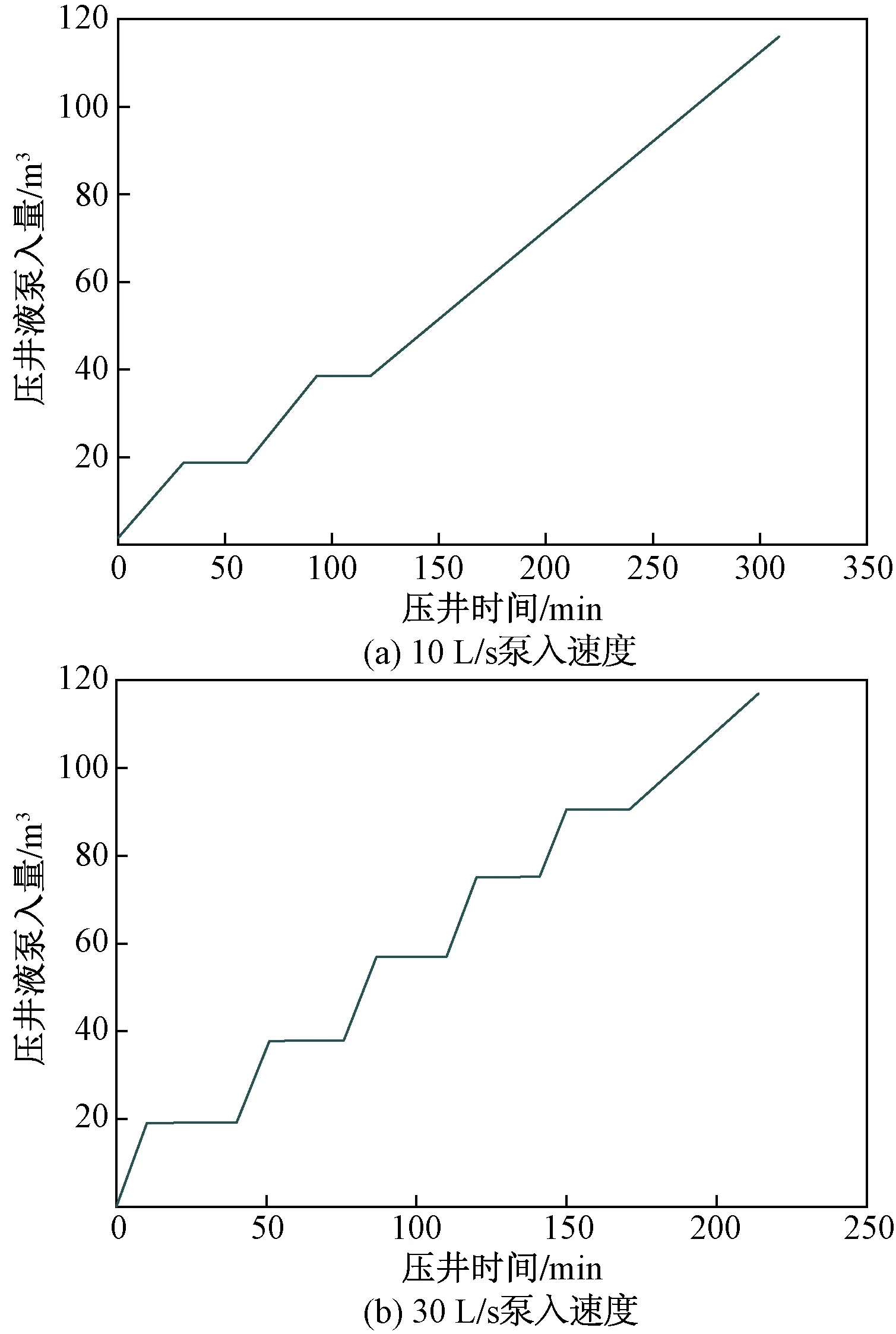
图5 不同泵入速度下压井液泵入量变化规律
3.2 模型验证
在对复合式置换法压井计算模型的准确性进行验证时,主要将模型的计算结果与Ramtahal[20]实验数据和任美鹏等[11]的动态置换法模型中的计算数据进行对比。在圆管直径为0.152 m,管口压力为297 K、管内体积为6.3 m3、液体密度为1.0 g/cm3的条件下计算的不同压井下气液注入速度比如表1所示。可以看出,在圆管直径、管口压力等相关基础参数一致的条件下,所建立的模型计算结果与Ramtahal[20]实验数据和任美鹏等[11]的动态置换法模型中的计算数据结果相比误差差别不大,因此本文复合式置换法压井模型的计算结果是准确可靠的。
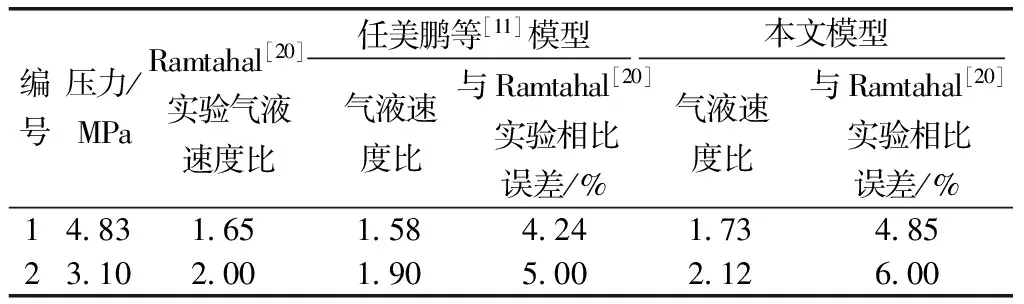
表1 气液速度比值
10 L/s泵入速度的复合式置换法压井模型与动态置换法压井计算模型对比如图6所示。可以看出,以10 L/s泵入速度的复合式置换法压井时间比动态置换法压井时间明显缩短且在压井后期套压值较低,但在同一压井时间内所需压井液泵入量高。
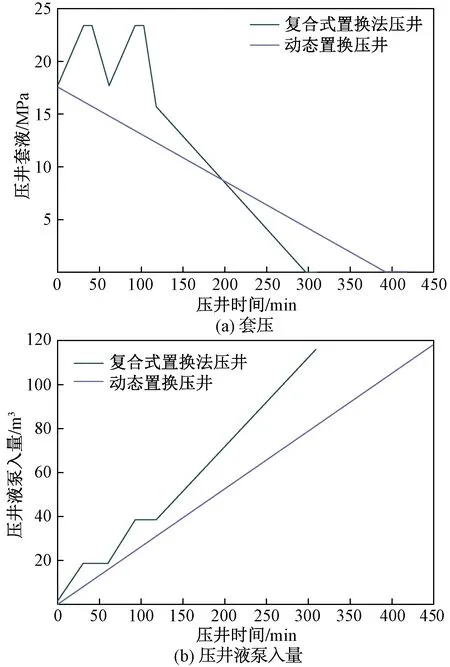
图6 不同置换法套压和压井液泵入量对比曲线
3.3 对比分析
对动态置换法压井进行优化。一种为始终保持4.6 L/s排量不变的一般动态置换法压井,一种为三段式动态置换法压井(第一次泵入19 m3压井液,泵入排量4.6 L/s;第二次泵入31 m3压井液,泵入排量6.2 L/s;第三次泵入66.5 m3,泵入排量8.2 L/s)。其压井套压和压井液泵入量随压井时间变化趋势分别如图7所示。可以看出,三段式动态置换法压井明显比一般动态置换法压井更具有优势,因此应用三段式动态置换法与复合式置换法进行接下来的对比分析。
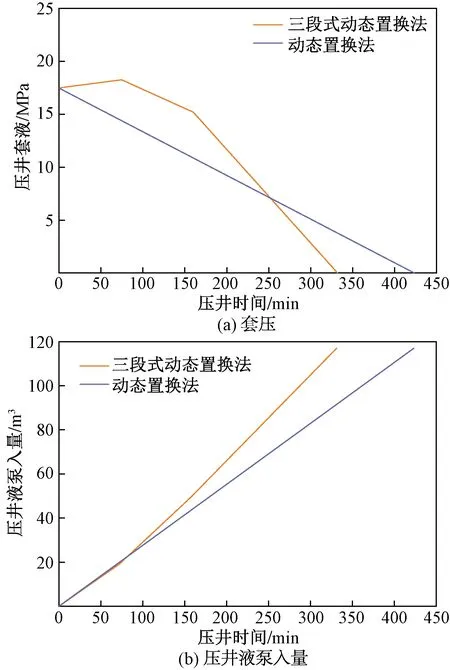
图7 不同动态置换法套压和压井液泵入量对比曲线
将三段式动态置换法压井与30 L/s泵入速度的复合式置换法压井进行对比。其压井套压和压井液泵入量随压井时间变化趋势分别如图8所示。
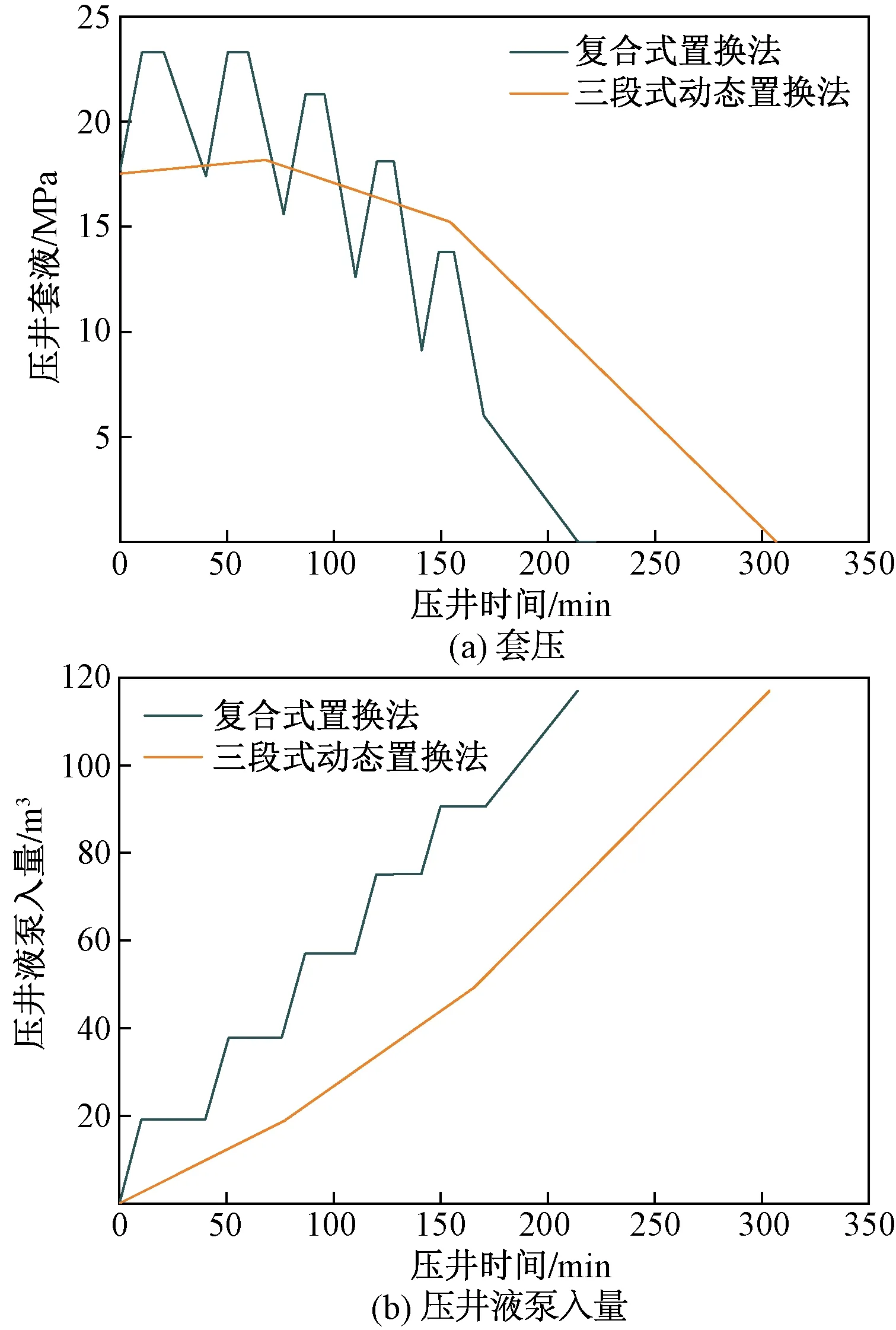
图8 不同置换法套压和压井液泵入量对比曲线
可以看出,与三段式比较,复合式压井所需时间更少,因此可知复合式置换法压井所需时间最少。
在实施置换法进行压井操作时,理想工况是压井液不随气体向井口装置运动。当液滴不被气体携带出井筒时,气体存在临界流量。在泵入压井液体积不变但气体临界流量不同的情况下,压井时间变化趋势如图9所示。
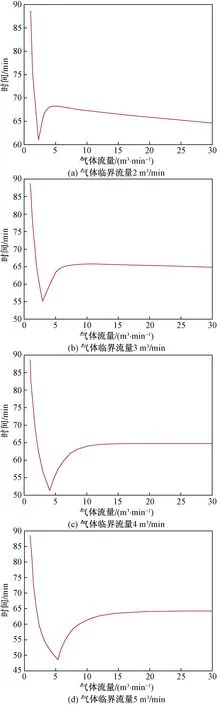
图9 不同气体临界流量下时间与气体流量关系曲线
可以看出,从开始排气到气体流量接近气体临界流量,因气体流量值较小,液滴基本不会被携带至井口故基本没有等待压井液下降时间,所以压井时间显著降低;当其大于临界气体流量时,因气体流量较大会增加等待压井液下降时间,所以总的压井时间增加;后期随着气体流量越大,压井时间基本不变且逐渐趋于稳定。因此,排气阶段最佳排气速度应略低于临界气体流量。
4 结论
(1)通过对所建立的复合式置换法压井模型验证可得,模型计算结果与Ramtahal[20]实验数据和任美鹏等[11]的动态置换法模型中计算结果具有较高的吻合度即误差值相差不大,因此,所建立的压井模型计算结果是准确可靠的。
(2)通过优化后的三段式动态置换法压井与普通动态置换法压井的压井时间和压井液泵入量的对比发现,优化后的三段式动态置换法压井能有效缩短压井时间。
(3)通过复合式置换法压井与优化后的三段式动态置换法压井的压井时间和压井液泵入量的对比发现,复合式置换法压井能更有效地缩短压井时间,提高压井效率,能更快使井内压力重新达到平衡,因此,复合式置换法压井在一定程度上可以用于指导现场压井作业。
(4)通过不同临界排气流量下压井时间随气体流量变化趋势可知,当排气阶段排气速度略低于临界气体流量时,压井时间最短,因此最佳排气速度应略低于气体临界流量。

