基于时域反射技术的电缆渗水缺陷检测方法

任志刚，赵雪骞，郭 卫，陈 平，周松霖，方春华

（1.国网北京电力科学研究院，北京 100075；2.三峡大学 电气与新能源学院，湖北 宜昌 430002）

0 引言

随着城市化进程的推进，电力电缆的使用量逐年增加，目前国家电网公司在运10～35 kV配网电缆线路总长度已超30 000 km。对于已经铺设于地下隧道或管井中的电缆，由于长期处于潮湿的地下环境中，电缆护层外的液体会通过小裂隙或者扩散效应逐渐渗入电缆内部引发电缆绝缘故障[1-5]。北京电力公司2005—2015年统计数据表明，电缆渗水缺陷所引发的故障约为134起，占电缆故障总数的37.6%。因此，对电缆内部渗水缺陷的及时和准确检测对提高电力系统稳定性具有重要意义。

国内外对于电缆缺陷的检测手段主要有超低频介损检测和振荡波检测法。振荡波检测法对于电缆渗水缺陷的灵敏程度很低，难以在渗水缺陷相关检测中发挥作用[6-9]。根据北京电力公司的运行经验，超低频介损检测是一种对渗水缺陷比较有效的检测方法，该方法虽然能够有效判断被测电缆是否含有渗水缺陷，但无法对缺陷进行定量识别及精确定位，亟需一种能够准确定位电缆渗水缺陷的方法。

时域反射技术（time domain reflection,TDR）是在被测物中注入1个快速上升脉冲，然后对反射波进行分析的远程测量技术。目前，TDR已从最初的军用测绘拓展到工业、农业、生物医学和航空航天等领域。但在电缆渗水缺陷检测方面，相关理论体系研究较少，对于渗水缺陷的适用频率、有效检测范围及特征波形识别等均需要研究[10-15]。

为得到TDR技术对于渗水缺陷检测的适用频率和检测范围，本研究在PSCAD平台上搭建仿真模型，模拟计算当电缆中存在渗水缺陷时，TDR检测的有效距离、不同频率对检测结果的影响以及渗水缺陷在TDR检测中的特征波形辨别方法，以期为准确识别渗水缺陷提供强有力的理论和数据支持。

1 仿真原理

TDR定位原理如图1所示。对于被测电缆，于t1时在测量端注入脉冲，脉冲沿电缆线芯传播，遇到阻抗不连续点A后产生反射波，测量端于t2时接收到反射信号，Δt为t1至t2经过时间，即脉冲在测试端口与阻抗不连续点之间传播一个来回距离所用时间，波速为v，缺陷位置为L=Δtv/2。

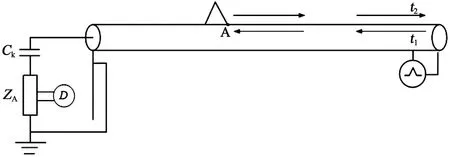
图1 TDR定位原理Fig.1 TDR positioning principle

为确定电缆中的波速v，对已知长度为L0的电缆，将其末端悬空，在首端接入TDR测试仪，在时间为t0时注入高频脉冲，接受脉冲自末端产生的反射波，得到波形返回时的时间t，则v可通过式（1）计算得到。

仿真模型中采用以呈脉冲函数形式的高斯脉冲离散电源来作为激励源，其时域形式为式（2）所示。

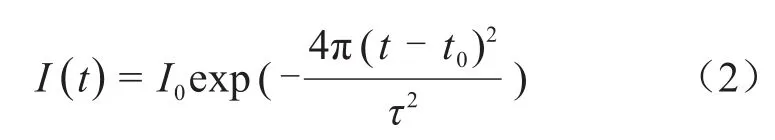
式（2）中：τ为脉冲的宽度；I0为激励源峰值；t0为脉冲峰值出现的时刻。取I0=5 A、τ=10-6、t0=1.5 μs时，激励源波形如图2所示。

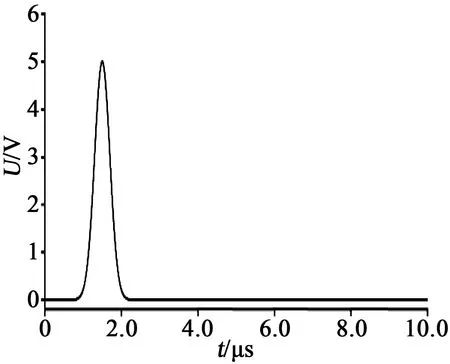
图2 高斯脉冲源仿真波形Fig.2 Simulation waveform of Gaussian pulse source

2 渗水缺陷检测有效范围

有效检测距离定义为当环境噪音为注入脉冲幅值的0.1%时，测量信号高于环境噪音的范围内TDR检测的最大距离。高频脉冲幅值在电缆中会迅速衰减，通过在仿真模型中注入不同频率的高频脉冲，并测量传播不同距离时的脉冲幅值，研究不同频率下幅值衰减的规律以及频率对衰减速率的影响。

通过PSCAD仿真软件建立总长度为5.0 km的电缆线路模型，其中分布5个中间接头，每个中间接头长度为0.59 m，模型参数依据10 kV交联聚乙烯电缆本体及预制型接头的内部结构和实际尺寸设置，所选缆芯外径为2.5 mm，电缆主绝缘层外径为7.2 mm，金属屏蔽外径为7.4 mm。护层采用两端接地的方式。对电缆线路注入的脉冲频率为107Hz，在电缆模型中设置多个传感器，将所有传感器依次接收到的激励源发射的波形绘制于图3中，可见在波形传播的过程中，波形逐渐展宽，幅值逐渐降低。

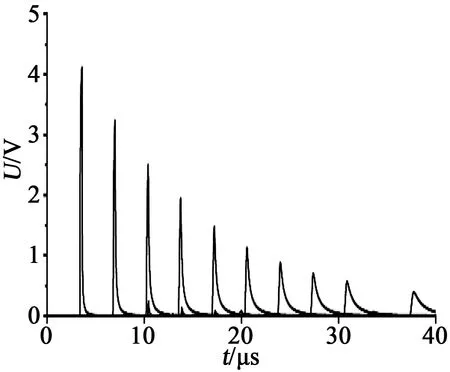
图3 脉冲幅值衰减曲线Fig.3 Pulse amplitude attenuation curve

取各次波形极值占初始值之比A及对应传播距离L进行函数拟合，得到频率为107Hz时电缆模型中幅值衰减的函数如式（3）所示，图4为拟合曲线。

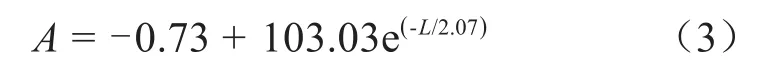
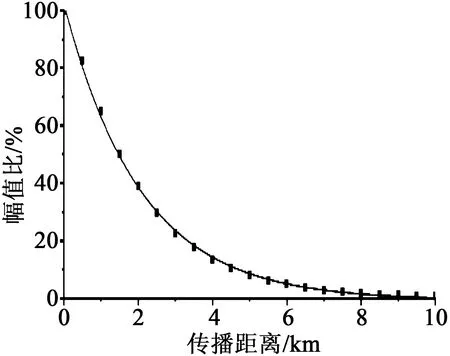
图4 脉冲极值拟合曲线Fig.4 Pulse extremum fitting curve

由式（3）可知，当A=0.1时，即TDR测量幅值等于环境噪音时，L=9.6 km。考虑到时域反射法需要波形在缺陷处返回，故对于所建立的电缆模型，107Hz下TDR对于渗水缺陷检测的有效距离为4.8 km。

为研究不同测试频率下，TDR检测渗水缺陷的有效距离，在105～109Hz内改变激励源频率，并重复上述步骤来研究脉冲频率的影响规律。以接收幅值为原幅值0.1%时的距离为相应频率下TDR检测的有效距离。因为仿真数据中仅可以获得各传感器处离散的电压幅值，无法精确得到幅值衰减至原幅值0.1%时对应的距离，所以通过拟合各峰值点得到幅值衰减与距离的函数关系式，然后计算出当A=0.1时的距离L，拟合曲线如图5所示。从图5可以看出，当频率为104Hz时，传播距离为10.92 km，而频率为109Hz时，距离缩短至4.68 km，即激励源频率升高使有效传播距离缩短。在106Hz前曲线下降不明显，平均下降幅度为2.1%，而在106Hz后曲线迅速下降，线性拟合后平均下降幅度为18.4%，即随着测试频率的升高，TDR对于渗水缺陷检测的有效距离迅速缩短。

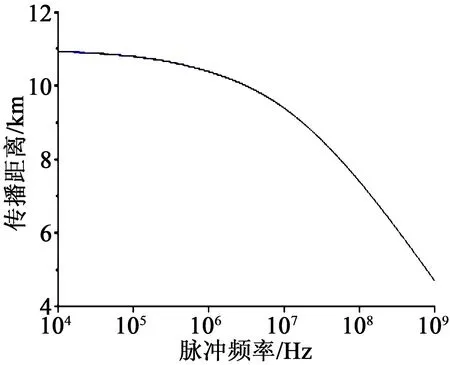
图5 激励源频率对有效传播距离影响Fig.5 Influence of excitation frequency on the effective propagation distance

脉冲波形在传播过程中会出现展宽的现象，同时由于脉冲频率对幅值衰减的影响较大，不同频率下可能会在同一位置产生不同特征的脉冲波形，进而导致渗水缺陷特征波形辨认误差。分别设置106、107、108Hz脉冲波作为激励源，并取相同位置渗水缺陷的反射波形，研究脉冲频率对波形特征的影响程度，仿真结果如图6所示。

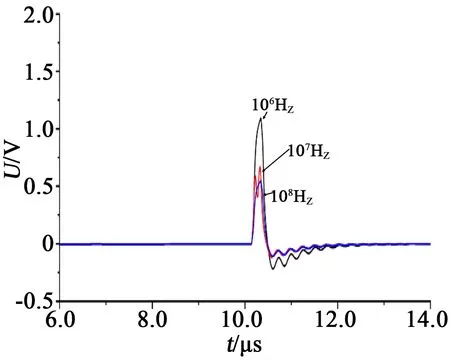
图6 不同输入频率下的波形Fig.6 Waveforms at different input frequencies

由图6可知，对于同一位置渗水缺陷，脉冲频率升高时，反射波幅值逐渐下降，平均降低幅度为35%。反射波中包含的特征波形不发生改变，即在不改变激励源幅值的情况下，不同频率脉冲仅会改变反射波的幅值，而不会改变特征波形。

综上，脉冲频率的上升会使TDR对于渗水缺陷检测的有效距离迅速缩短，且测量幅值降低，但不影响脉冲反射波形的特征。但是由于不同频率的脉冲宽度τ不同，若反射脉冲在t=τ之前返回，则入射波会与反射波重叠产生测试盲区，导致测量结果失效，于是在测量频率的选择上需要考虑脉冲宽度对于测试结果的影响。当测试盲区小于1 m时，此时脉冲宽度τ=1/v=0.64×108，即测试频率需高于1/τ=1.56×108Hz，此时对应的测量有效距离为3.76 km。

3 渗水缺陷特征波形特征

在使用TDR技术对电缆的检测过程中，可能会针对电缆中各种阻抗不连续点产生对应特征波形，其中包括中间接头、低阻接地点、开路点、渗水缺陷等。在对渗水缺陷定位时，需要从各反射波形中区分出渗水缺陷的特征波形。为此，在电缆模型中计算上述不同阻抗点在TDR检测下的反射波形。

3.1 中间接头反射波

中间接头的结构与电缆不同，对于整段电缆传输线而言，中间接头也可以看做一类特殊的阻抗点。高频脉冲传播至此会产生一次极化-去极化的波形，仿真得到的中间接头反射波形如图7所示。图中包含3次反射波和1次复反射波，分别为0.5、1.5、2.0 km处中间接头反射波和0.5 km处中间接头的复反射波。

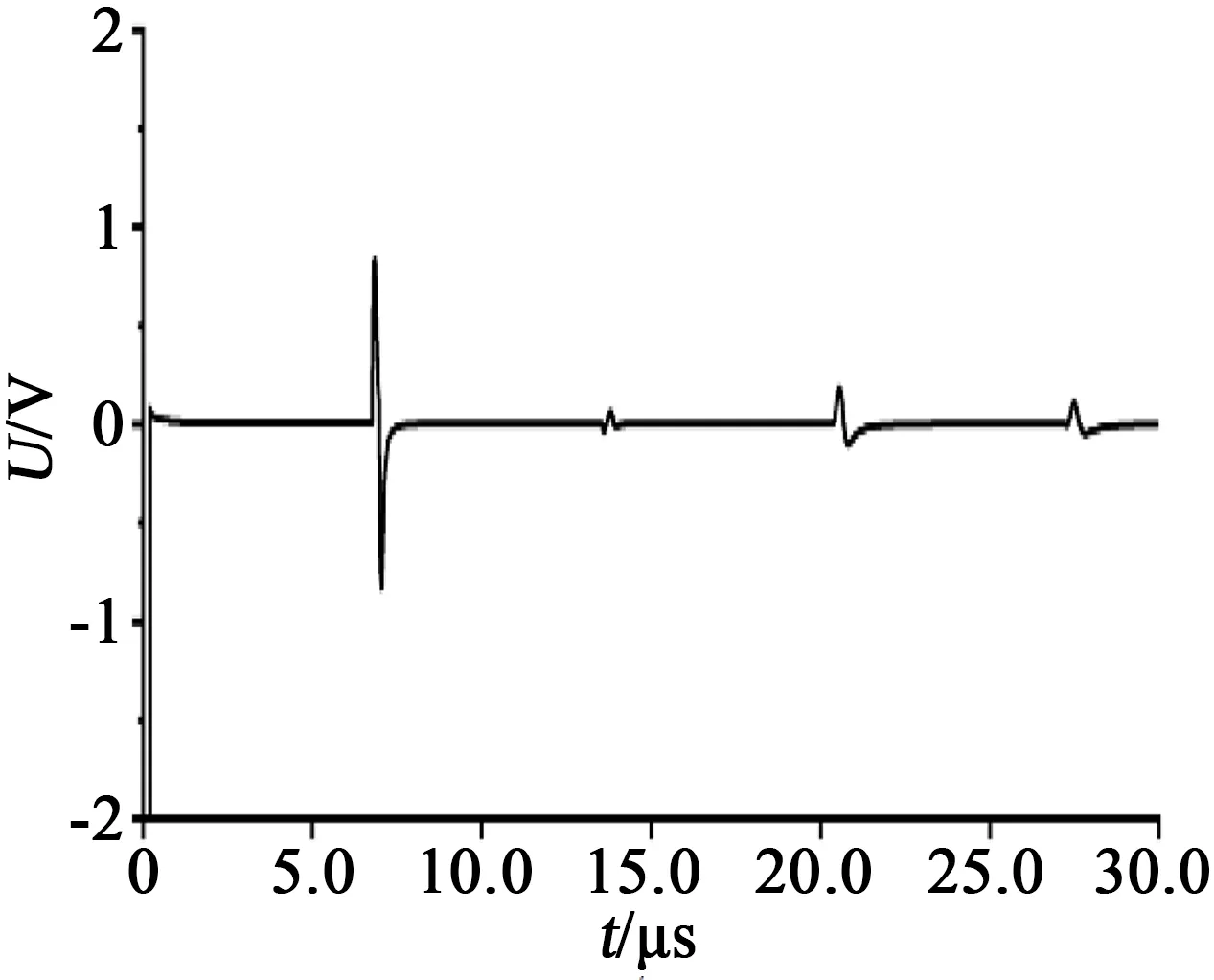
图7 中间接头反射波Fig.7 Reflected wave of intermediate joint

根据式（3）计算可知，注入脉冲在到达0.5 km处中间接头时其幅值为4.01 V，其反射波幅值为1.1 V，可得中间接头反射系数为0.274，即脉冲波在经过中间接头时会有27.4%的反射，72.6%将继续沿线路传播。

3.2 低阻接地反射波

在实际生产运行中，电缆可能会遭受外力或人为破坏，导致电缆对地绝缘损伤，缆芯对地电阻大幅降低。在仿真计算中，使电缆缆芯在距首端1.0 km处通过较低的阻抗接地，反射波形示于图8。从图8可以看出，接收端在12.8 μs时记录了1次负方向反射波，该反射波是高频脉冲经过低阻接地点时产生的。

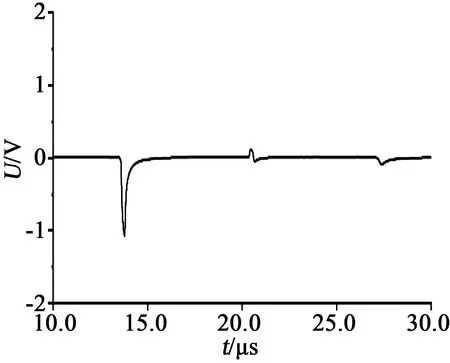
图8 低阻接地反射波Fig.8 Reflection wave of low resistance ground point

3.3 开路点反射波

TDR检测时需将电缆末端悬空，当脉冲到达电缆末端时会产生反射波形。仿真计算中，在距电缆首端0.5 km处设置开路点，高频脉冲在经过该点时的反射波形如图9所示。从图9可以看出，接收端于6.4 μs时首次得到一次反射系数为正的反射波，并于12.8 μs时接收到其复反射波。对比传播幅值可得，开路点处反射系数为1，即当TDR检测波形中出现较高幅值的脉冲波形时，判断为电缆中的开路点。

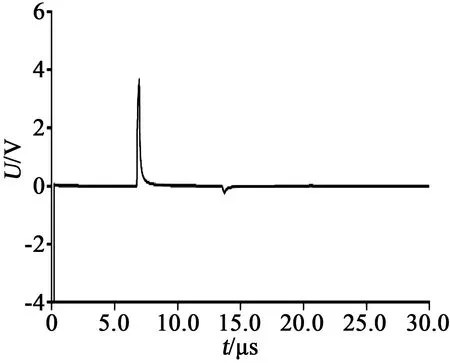
图9 开路点反射波Fig.9 Reflection wave of open point

3.4 渗水缺陷反射波

渗水会导致电缆绝缘层外侧覆盖一层水膜。仿真设置水膜覆盖于绝缘层外，其中0.5 km处为渗水点，1.5 km处为中间接头对照。将缺陷模块加入模型进行计算，结果如图10所示。

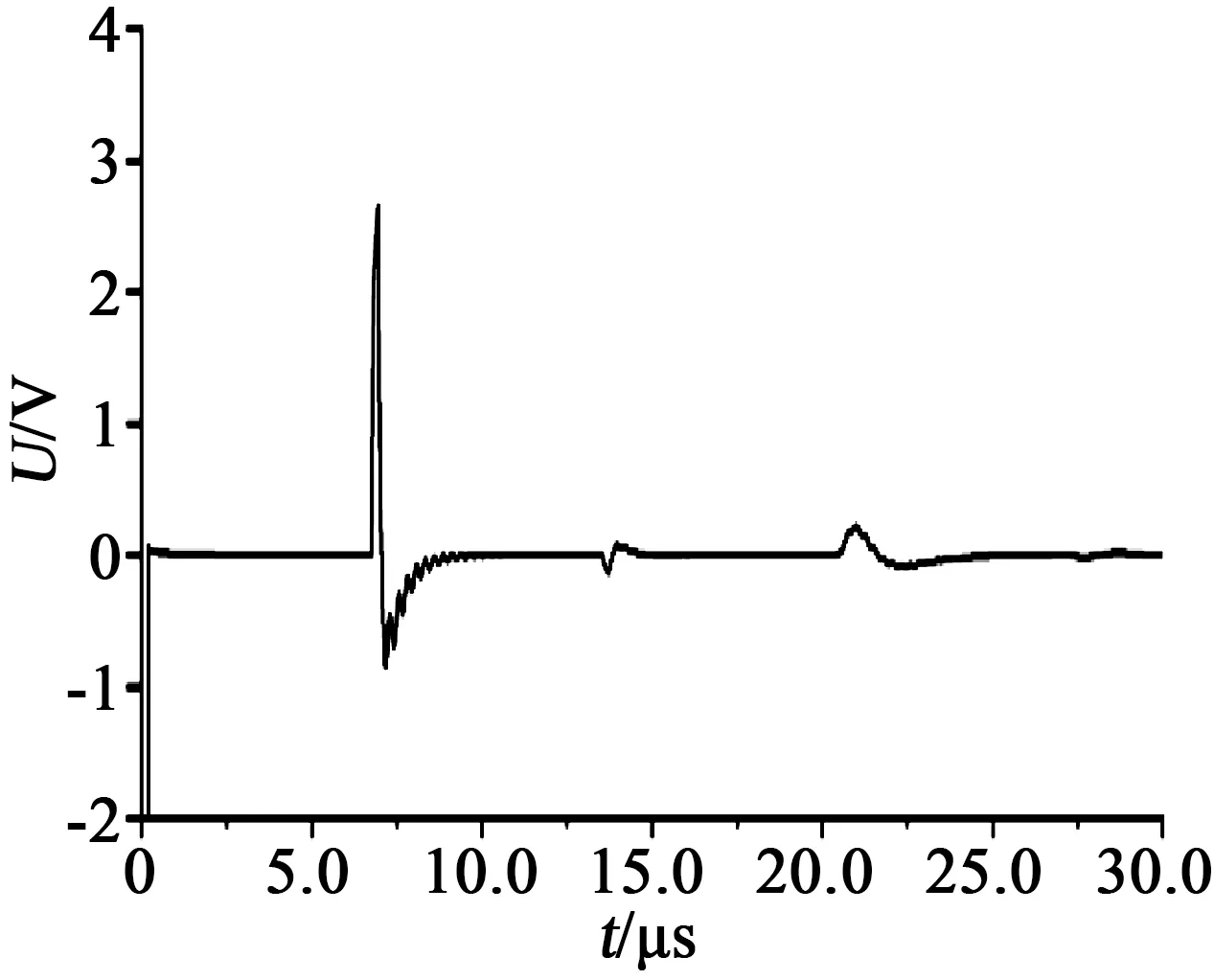
图10 轻微渗水电缆反射波Fig.10 Reflection wave of cable with slight water penetration

从图10可以看出，在6.4 μs（0.5 km）处有1次反射波，其幅值为2.5 V，高于相同位置中间接头的反射波幅值。12.8 μs（1.0 km）处为该回波的复反射波，19.2 μs（1.5 km）处为中间接头与渗水缺陷的复合回波，但由于渗水缺陷的复反射波已经极其微弱，可以认为该波形仅为中间接头处的反射波，相比图7中1.5 km处中间接头反射波，该处反射波形产生了幅值衰减和展宽，其反射系数为0.18。同时由于渗水会改变渗水缺陷处的水膜电容，TDR的检测波形也会产生改变。仿真中计算了严重渗水缺陷的情况，并将单位长度水膜体积设置为10 mm3，仿真计算结果如图11所示。

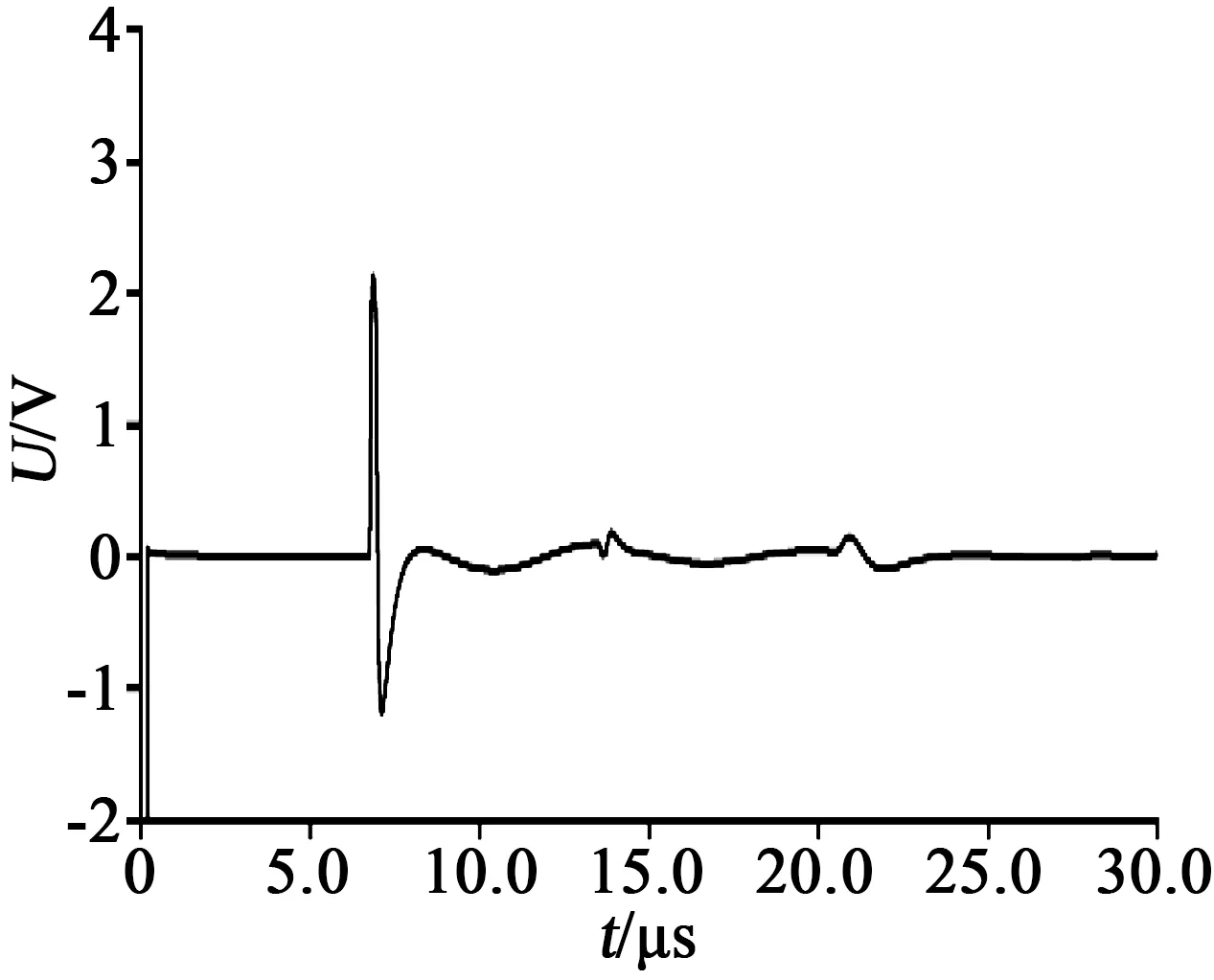
图11 严重渗水电缆反射波Fig.11 Reflection wave of cable with serious water penetration

对比图10～11可以看出，在改变渗水缺陷的严重程度后幅值未发生明显改变，轻微渗水情况下的缺陷反射波在峰值后会有少量振荡产生，使其波形与严重渗水情况表现出少许差别，但不影响整体波形特征的辨别。

以上对TDR检测中可能出现的中间接头、低阻接地点、开路点、渗水缺陷特征波形进行了分析，根据以上分析能够在TDR测量结果中辨认出包括渗水缺陷在内的不同阻抗点，进而进行精确定位。

4 渗水缺陷定位方法

仿真试验设置的电缆模型总长度为1.4 km，末端使用高阻接地，在电缆中设置了两处中间接头，另分别在不同位置设置了渗水缺陷和短路点缺陷作为对照。图12为接收端记录的波形图，图12中共包含有P1～P5共5次明显反射波形，分别在2.6、6.4、11.5、12.8、17.9 μs时被接收端记录。由于电缆末端高阻接地，在17.9 μs时接收的波形即为注入脉冲在到达电缆末端时产生的反射波。根据式（1）计算可知，该电缆中的波速v=1.56×108m/s，前4次反射波形分别来自于0.2、0.5、0.9、1.0 km处的不连续阻抗点，根据前文总结的阻抗点特征波形，可知0.2 km和0.9 km处为中间接头反射波，0.5 km处为渗水缺陷反射波，1.0 km处为低阻点反射波。除上述5个明显反射波之外，还存在少许幅值较低的波形，为反射波在经过各阻抗点时产生的复反射波。

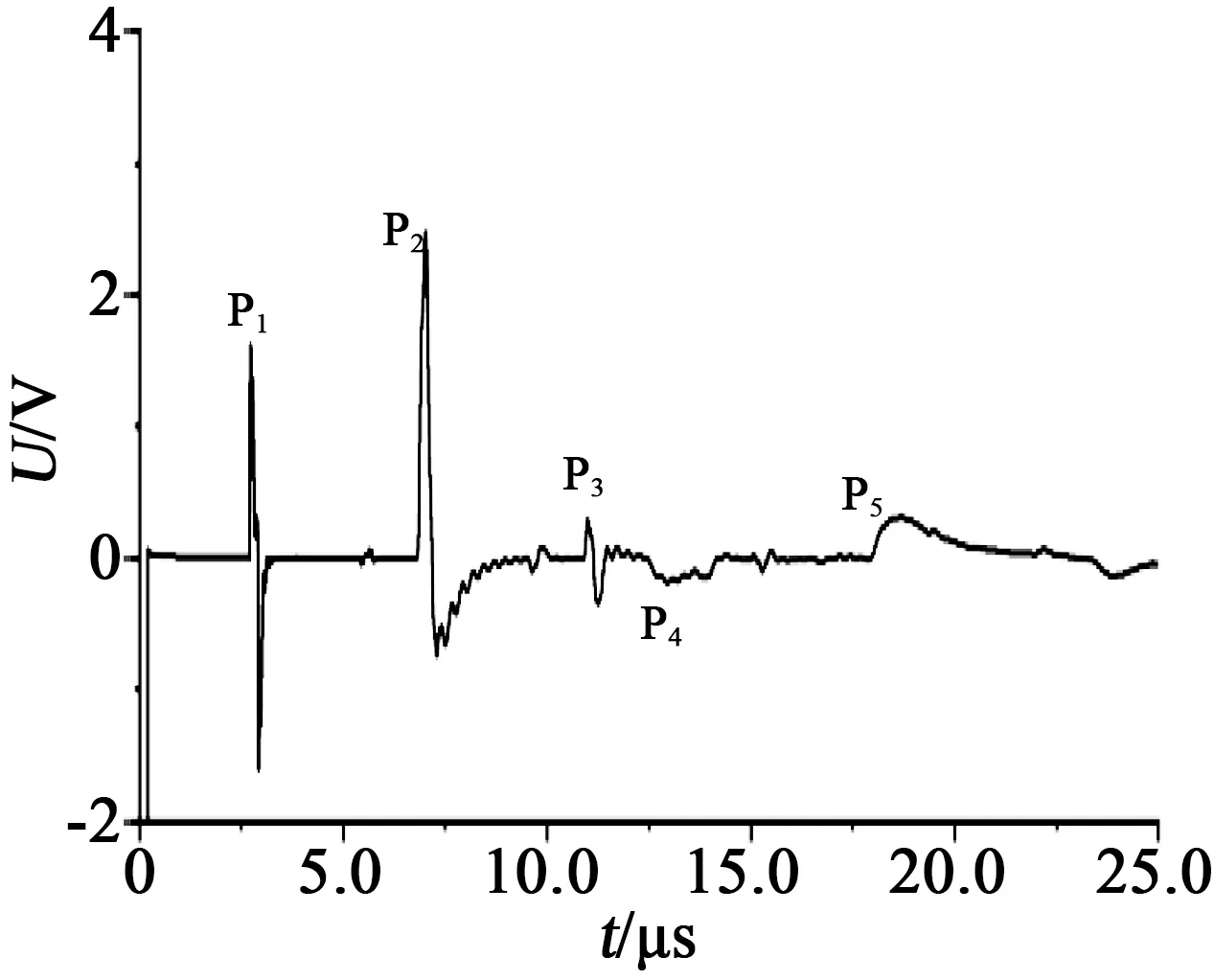
图12 TDR仿真波形图Fig.12 TDR simulation waveform

为验证阻抗点特征波形是否与阻抗点位置相关，改变渗水缺陷模型与首端的距离，自0.5 km处变更为0.2 km与0.9 km的位置，并分别进行了检测试验，结果如图13所示。

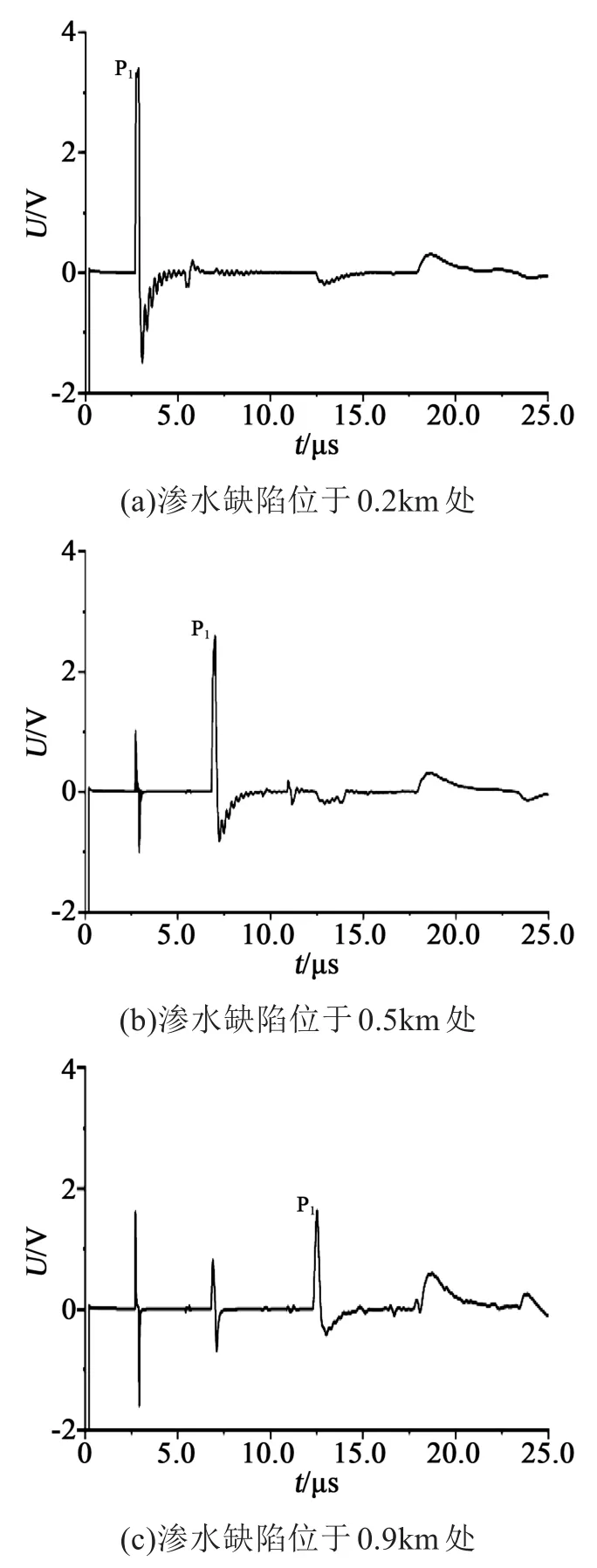
图13 不同位置的渗水缺陷Fig.13 Water seepage defects at different positions

图13中通过P1标注了渗水缺陷的波形，可见随着缺陷与接收端距离的增大，其波形的幅值减小，且存在小幅度的展宽，但波形特征不变，仍然能够在TDR的检测结果中辨认出渗水缺陷反射波，并通过反射波到达时间进行定位。

5 复反射波对定位精度的影响

由于接收元件在传输路径中也属于阻抗不连续点，也会产生一次反射波，该反射波会再次注入回路中，称之为复反射波。复反射波具有与反射波相同规律的传播特性，在每次经过阻抗点时会发生一次折返射，通常反射波会比入射波小将近1个数量级，因此在考虑多阻抗点影响时，由于2次复返射波会经过至少3次反射，波形幅值极小，故仅考虑首次复反射波对于渗水缺陷反射波产生的干扰。

由于测量对象为接收脉冲的时间与波形，且电缆中阻抗点的位置随机分布，TDR检测结果中，反射波形通常会在时间轴上交错排列，相互间不会干扰。但是，若两阻抗点距首端的距离接近整数倍关系时则会产生干扰。通过仿真得到的复反射波幅值占比与反射系数的关系如图14所示。从图14可知，当反射系数超过0.32时，复反射波占比超过10%，即复反射波幅值会与反射波同数量级，此时会对TDR测量精度产生影响。

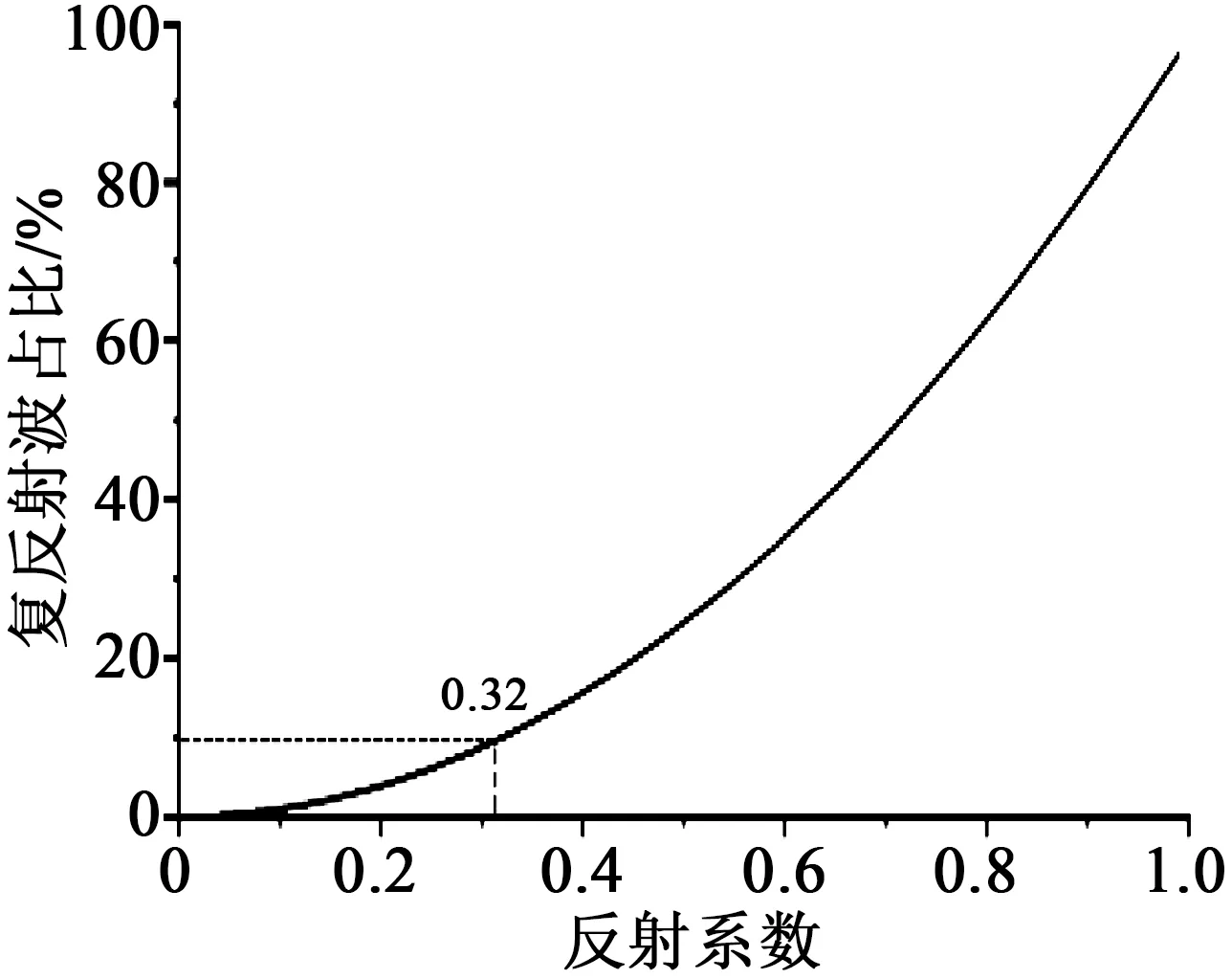
图14 反射系数对复反射波的影响Fig.14 Effect of reflection coefficient on the complex reflection wave

6 特征波形试验验证

为验证渗水缺陷在TDR检测下的特征波形，对1段退运的正常电缆按以下方法分别模拟正常电缆、轻微和严重渗水电缆，对这3种工况电缆进行TDR测试，获得相应的波形。

试验电缆型号为YJV22-3×120，长度为404 m，其中位于178 m处有1个中间接头。在电缆接头处设置轻微渗水、严重渗水缺陷。为模拟轻微渗水电缆缺陷，通过注射器将400 mL盐水按10 cm间隔分别注入至防水护套内部，使盐水能够通过电缆屏蔽层位于绝缘层与护套之间。进行TDR检测后，再次注入700 mL盐水以模拟严重渗水电缆缺陷，并进行TDR检测。由于3次检测波形类似，仅中间接头处测量波形存在区别，故通过图15展示3次测量中接头处对应波形。

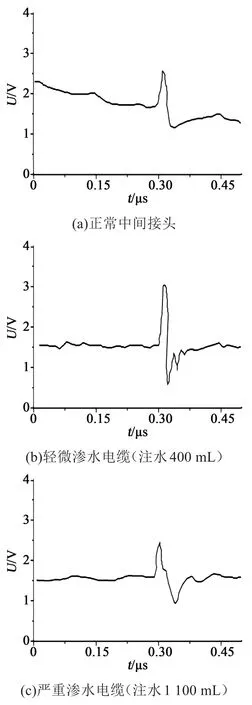
图15 不同渗水程度下的TDR波形Fig.15 TDR waveforms under different water penetration

图15(a)为正常电缆中间接头的检测波形，波形特征表现为一次极化-去极化电流波形，其幅值较低；图15(b)为轻微渗水电缆的检测波形，其幅值相比于中间接头高约29%，同时波尾出现欠阻尼振荡，振荡波形周期约为0.02 μs，频率约为50 MHz；图15(c)为严重渗水电缆的检测波形，幅值比轻微渗水低43%，同时尾端振荡波形周期约为0.04 μs，频率约为25 MHz。对比图14中3种波形可知，中间接头与渗水缺陷存在不同的特征波形。当电缆中存在渗水缺陷时，其特征波形为一次正向脉冲，且尾端有振荡波形，随着渗水程度的加深，波形幅值下降，振荡频率降低。

7 结论

（1）TDR技术能够检测出电缆内部的渗水缺陷，但测试频率需高于1.56×108Hz，有效检测距离约为3.76 km。

（2）渗水缺陷检测返回波形受电缆内部缺陷反射系数的影响，当反射系数大于0.32时会影响到特征波形识别。

（3）不同类型的缺陷在TDR检测中会返回不同的特征波形，当渗水程度不同时，波形幅值和波尾振荡也会改变。