基于分段常数水平集方法的声振耦合系统拓扑优化

苗晓飞， 赵文畅， 陈海波

(中国科学技术大学 近代力学系 中国科学院材料力学行为与设计重点实验室，合肥 230026)

近些年来，结构振动和声学优化问题因其在结构减振降噪方面的重要应用前景而成为国际上的研究热点之一[1]，减少结构关键区域的振动与声辐射的研究工作也屡见不鲜。拓扑优化作为一种灵活的结构优化手段，可以从本质上改变结构的拓扑形式，在满足工作要求的前提下改善结构性能和减轻结构质量，经济且美观，已成为近年来结构优化领域研究的热点。

1988年，Bendsøe等[2]首先提出将均匀化方法引入到连续体拓扑优化中，揭开了连续体结构拓扑优化的开端。在此之后，变密度法、渐进结构优化方法(evolutionary structural optimization，ESO)和水平集方法(level set method，LSM)等[3-7]越来越多的优化算法不断地被提出。拓扑优化方法的不断发展给振动控制提供了新的思路，越来越多的学者开始将各种优化算法运用到振动控制的优化问题中。房占鹏等[8]基于双向渐进优化算法，以最大化模态损耗因子为目标进行了约束阻尼板的拓扑优化问题研究；Zhang等[9]基于固体各向同性材料惩罚模型 (solid isotropic material with penalization，SIMP)插值，以最小化结构指定位置处的振动水平为目标对自由阻尼板阻尼材料的分布进行了优化；Zheng等[10]利用遗传算法研究了以减少结构振动幅值为目标的阻尼材料的最优分布问题;Xia等[11]以最大化结构一阶频率为目标，利用水平集算法进行了拓扑优化设计。目前，在结构拓扑优化问题中，大多仅考虑结构自身而忽略了周围介质对于结构响应的影响。当然，在结构处于类似空气这类密度相对结构很低的介质环境下，这种忽略是合理且简便的；而当结构处于水这类相对密度较大的介质中，则必须考虑流体介质和结构之间的相互作用，即强耦合作用。这类流固耦合系统下的拓扑优化工作已开始引起学者们的注意。商林源等[12]利用放松的优化准则法研究了声结构耦合系统的双材料拓扑优化问题；Shu等[13]基于水平集方法，考虑了最小化声振耦合系统内声场声响应的优化问题。Akl等[14]以板的厚度为设计变量，考虑了板与声腔的耦合系统的拓扑优化问题。由于有限元数值模拟方法对于无限大声场分析具有一定的局限性，前面这些工作考虑的都是有限的声场问题。边界元方法由于可以自动满足无限远处的辐射边界条件，对于处理无限大声场问题具有天生的优势，近年来基于有限元-边界元耦合的外声场问题的拓扑优化工作也得以实现[15-16]。目前上述工作考虑的目标函数都是声压值或辐射声功率这类声场物理量，忽略了对结构响应的考察；同时也多是基于密度插值和移动渐近线方法展开的，其他优化算法在这类优化问题中的效能还有待考察。

分段常数水平集(piecewise constant level set，PCLS)方法由水平集方法演化而来，最早由Christiansen等[17]提出。由于它可以很好的克服传统水平集方法存在的依赖初始符号距离函数和无法自动生成新的孔洞等较为明显的弊端，同时避免了重新初始化的过程，逐渐被一些学者用于结构拓扑优化中[18-19]。但是这类方法一般需要利用拉格朗日乘子法或增广拉格朗日乘子法来满足约束条件，而拉格朗日乘子的更新是较为复杂和麻烦的，难以准确表示其变化规律[20]，往往出现随优化问题的变化而改变的情况，需要通过经验来判断，使方法的广泛使用受到限制。

本文基于分段常数水平集方法，考虑了结构与声场双向耦合作用，以有限元-边界元耦合系统下结构指定位置处振幅的平方为目标函数，进行了双材料的拓扑优化设计。采用伴随变量法进行灵敏度分析，引入二次罚函数方法使优化问题变为无约束优化问题，核心处理是基于灵敏度信息对优化参数进行了重新定义，克服了参数的问题依赖性。最后基于最速下降方法进行设计更新，最终得到了双材料的最优分布。

1 有限元-边界元声振耦合分析

考虑结构与无限大声场的强耦合系统，如图1所示。结构Ω振动向声场Ωf辐射声压，声场反作用于结构，影响结构的振动。图中：Γ=Ωs∩Ωf为结构与声场的耦合边界；ns，nf分别为结构与声场耦合界面处的外法向向量；fs为直接作用在结构上的结构载荷。分别采用有限元和边界元方法对结构和声场进行离散近似。

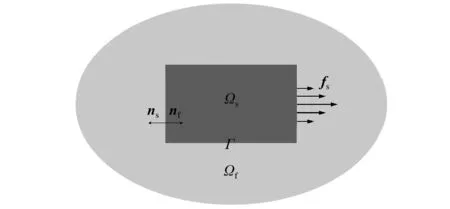
图1 声振耦合系统Fig.1 Coupled structural-acoustic systems

1.1 结构有限元分析

对于简谐激励作用下的结构，其振动控制方程可以写为

(-θ2M-iθC+K)u=Kdu=f

(1)

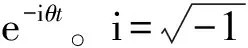
基于瑞利阻尼模型，阻尼阵C可以写为

C=αM+βK

(2)

式中，α和β为材料的瑞利阻尼系数。

在考虑声场对结构的反作用时，外载荷可以写为

f=fs+fp

(3)

式中：fs为结构载荷；fp为声场载荷。

1.2 声场边界元分析

简谐形式下的声场Helmhotz方程可以表示为

∇2p(x)+k2p(x)=0

(4)

式中：p为声压；k=θ/cf为波数，cf为波速。通过格林第二公式并将点x逼近边界即可得到常规边界积分方程(conventional boundary integral equation，CBIE)

(5)

将式(5)两边同时对源点x所在边界外法向方向求导，即可得到超奇异积分边界方程(hypersingular boundary integral equation，HBIE)

(6)

式中：y为场点；q(y)=∂p(y)/∂n(y)为声通量；系数c(x)由点x处的几何性质决定，对于光滑边界，c(x)=0.5；G(x,y)为格林函数，对于三维声场问题，可以写为

(7)

式中，r=|x-y|为源点与场点的欧式距离。

进行外声场分析时，由于式(5)或式(6)单独使用会引起解的非唯一性问题，因此Burton等[21]提出了将两式进行线性组合的Burton-Miller方法

CBIE+αHBIE=0

(8)

式中，α为耦合系数，建议取为-i/k[22]。通过配点法对式(8)进行离散，可得声场控制方程

Hp=Gq

(9)

式中，H和G为边界元系数矩阵。

1.3 有限元-边界元耦合分析

考虑结构与声场的双向耦合作用，需要考虑耦合面上位移与力的平衡条件

vf(x)=-iθu(x)·nf(x)

(10)

σ(x)·ns(x)+p(x)·nf(x)=0

(11)

式中：vf为耦合边界处声场介质的法向速度；σ(x)为耦合边界处结构应力。在式(10)、式(11)两端分别乘以结构和声场的插值形函数φf，φs并在耦合边界上积分、离散后得到耦合边界平衡方程

vf=-iθS-1Cfsu

(12)

fp=Csfp

(13)

式中：Csf和Cfs为结构与声场耦合转换矩阵；S为边界质量矩阵，可以表示为

(14)

(15)

(16)

式中：Ns，Nf为形函数φs，φf的矩阵形式；n为nf的矩阵形式。

又由第二类边界条件

q=iθρfvf

(17)

式中，ρf为声场介质密度。将式(12)、式(17)代入式(9)中可得

Hp=θ2ρfGS-1Cfsu

(18)

联立式(1)、式(18)即可得到基于有限元-边界元方法的声振耦合系统控制方程

(19)

2 优化问题描述

如图2所示，对于双材料的拓扑优化，优化的目的是要确定两种材料的最优分布形式。在本文中，我们以材料二作为设计材料，即确定材料二的分布形式，其余部分则全设为材料一。在分段常数水平集方法中，我们将引入PCLS函数φ(x)来表示两种材料的铺设区域

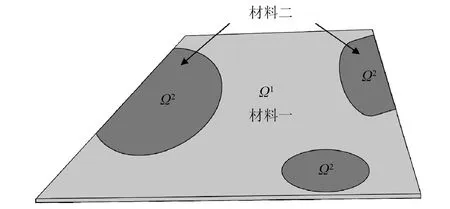
图2 基于PCLS方法的双材料分布Fig.2 Bi-material distributions based on PCLS method

(20)

即在整个设计区域Ω内，PCLS函数保持为常数，在材料一铺设区域Ω1为1，在材料二铺设区域Ω2为2。

基于PCLS函数的单元刚度阵K(e)与质量阵M(e)可分别表示为

K(e)(φ)=(φ-1)K2(e)-(φ-2)K1(e)
M(e)(φ)=(φ-1)M2(e)-(φ-2)M1(e)

(21)

基于瑞利阻尼假设，单元阻尼阵C(e)可以表示为

C(e)(φ)=(φ-1)(α2M2(e)+β2K2(e))-
(φ-2)(α1M1(e)+β1K1(e))

(22)

式中：上标1和2分别为材料一与材料二；α1，β1，α2，β2分别为两种材料的瑞利阻尼系数。

于是，基于PCLS函数的结构整体刚度阵、质量阵与阻尼阵可以表示为

(23)

式中，Ne为结构单元个数。

而作为设计材料的材料二体积可以表示为

(24)

因此，在考虑材料体积约束时，基于分段常数水平集方法的以结构振幅平方为目标的拓扑优化问题可以表示为

s.t.Kd(φ)u(φ)=fs+Csfp(φ)

Hp(φ)=θ2ρfGS-1Cfsu(φ)

(25)

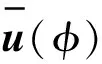
3 灵敏度分析

基于分段常数水平集方法，目标函数依赖于PCLS函数φ(x)，在计算灵敏度信息时，我们需要对目标函数进行变分。本文中，灵敏度分析采用的是Zhao等使用的伴随变量法。

首先引入原目标函数的等价形式

(26)

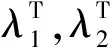
(27)

由于伴随向量的任意性，有

(28)

(29)

(30)

基于式(1)、式(21)、式(22)可得

(31)

[α2M2(e)+β2K2(e)]-[α1M1(e)+β1K1(e)],

(32)

于是，基于分段常数水平集方法的单元灵敏度可以表示为

(33)

针对本文的目标函数，则有

(34)

联立式(28)～式(34)，即可得到基于分段常数水平集方法的单元灵敏度。

4 算法流程

对于体积约束条件，我们将引入二次罚函数的方法来满足体积约束，最终修正的目标函数可以写为

(35)

式中，μ为体积惩罚系数。修正后目标函数的单元灵敏度可以写为

(36)

不同于水平集算法的是，在每代优化中，PCLS函数都是定义为1或2，因此需要定义一个算法，使PCLS函数再次满足约束式(20)，即

(37)

我们通过最速下降方法来更新PCLS函数，即在每个单元中

(38)

式中，τ(k)为时间步长，在第k代迭代步中，设为

(39)

式中：h为单元的最小尺寸;ζ∈(0,1)为一常数。

而在第k代迭代步中，Zhang等(2019年)将体积惩罚系数μ(k)设为

(40)

式中，t和μmax为给定常数，用于保证体积约束得以满足。然而，μ(k)在这种定义下是与目标函数J(φ(k))相关的，在计算的过程中可以发现，参数t与μmax存在较大的问题依赖性，即随着优化算例的改变，参数的变化较大，不具有一般性，往往需要通过调试才可获得。Zhang等研究中不同优化算例选择不同的优化参数同样可以看出这一点。因此，我们从灵敏度的角度出发，对参数μ(k)的数值进行了重新定义

(41)

式中，ε∈(0,1)为一常数。由于PCLS函数的更新是直接依赖于灵敏度信息的，式(41)中μ(k)的数值则直接与目标函数灵敏度绝对值的最大值相关，因此更具有一般性。参数ε用于保证优化可以稳定光滑的进行。经过测试，本文将ζ均取为0.05；ε均取为0.2；μmax均取为10。

至此，基于分段常数水平集方法的拓扑优化流程总结如下：

步骤1建立有限元-边界元耦合模型，初始化PCLS函数，获得结构有限元与声场边界元矩阵M，K,C,H,G,Cfs，Csf确定常系数矩阵Q，给定常数ζ,ε,μmax。

步骤2通过求解式(19)获得结构位移与声场声压，进而由式(25)计算目标函数J(φ)。

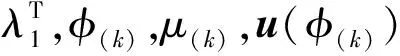
步骤4引入内循环，更新φ(k+1)。

①计算

式中，τ(k)由式(39)计算得到。

步骤5检查外循环终止条件，如果满足，则退出循环；否则回到步骤2。

5 算 例

本章中，我们考虑一水下立方壳体在点激励作用下的优化算例，立方壳外部空间为水，不考虑立方壳内部介质的耦合影响，约束结构底面的平动自由度，如图3所示。立方壳体边长为1 m，壳厚度为0.02 m，在其上表面中心有一点简谐激励F=F0e-iθt，F0=105N频率f=120 Hz。结构每个面划分为40×40个四节点壳单元，共9 600个单元，声场部分采用匹配的四节点常量元与结构进行耦合。

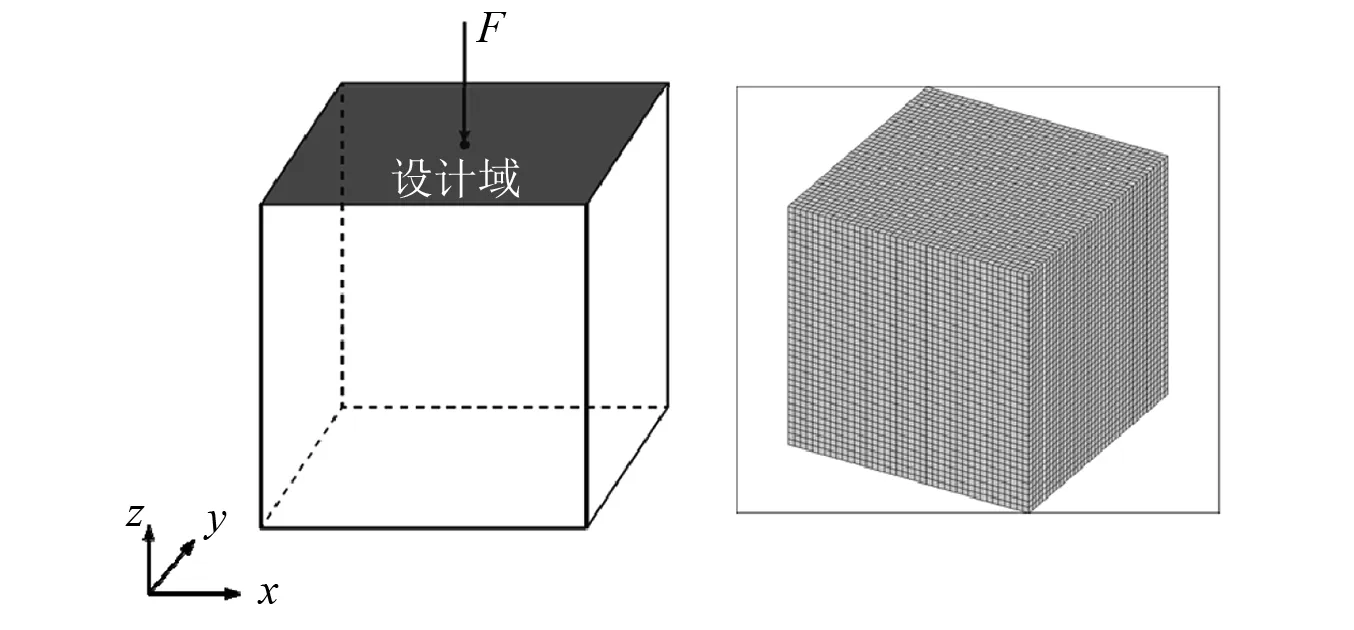
图3 立方壳结构及网格划分Fig.3 The cubic shell structure and the mesh

假设结构由两种不同的强弱材料组成，弱材料的杨氏模量和密度为强材料的十分之一，具体的材料属性如表1所示。假设两种材料的瑞利阻尼系数相同，都设为α=0.1,β=0.001。由于结构上表面对于结构响应的影响最大，因此选择立方壳的上表面作为设计区域。结构其余部分全部设为弱的基体材料，且其余部分同上表面一样可以振动向外辐射发声，以强材料为设计材料。目标函数选为加载点处z向幅值的平方，体积约束V=|Ω|/2。

表1 水下立方壳材料参数

为验证本文所用伴随变量法的正确性，我们将PCLS函数φ(x)放松到[1,2]的连续空间，采用差分法计算目标函数的灵敏度同本文的伴随灵敏度进行比对。图4给出了120 Hz时初始全为弱材料，摄动值为1×10-4时前200个单元的伴随灵敏度与差分结果的比对结果。可以看出二者吻合良好，说明了本文伴随变量方法的正确性。

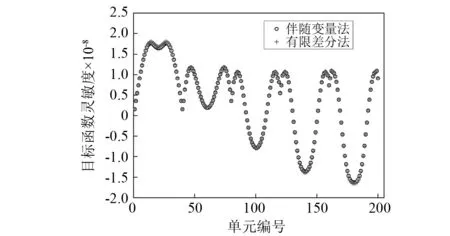
图4 伴随变量法与有限差分法灵敏度结果对比Fig.4 Comparison of sensitivities obtained by the adjoint method and finite difference method

初始PCLS函数设为φ(0)=1，即结构上表面全由弱材料组成。目标函数与体积约束函数的收敛历史，如图5所示。为了考察目标函数的收敛性，在已经收敛的情况下继续往后共计算了90代。从图5中可以看出，随着迭代的进行，目标函数迅速下降，经过62次迭代后，目标函数和体积约束函数都已收敛。目标函数从5.019×10-5m2降到了1.408×10-6m2。为进一步说明优化的有效性，计算了结构上表面全为强材料时的目标函数，其值为2.374×10-6m2，高于体积约束为0.5时的优化设计值，也说明了该优化问题的非线性。

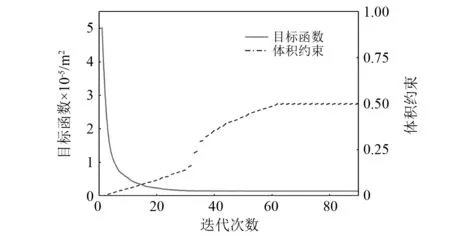
图5 120 Hz时目标函数与体积约束的迭代历史Fig.5 Iteration histories of objective function and volume constraint at 120 Hz

图6给出了不同迭代步数下材料的分布情况，图6中浅灰色部分代表强材料，黑色部分代表弱材料。可以看出强材料的占比在稳步提高，最终优化后的材料分布如图6(d)所示。优化前后的结构z向振幅云图，如图7所示，可以看出优化的效果显著。

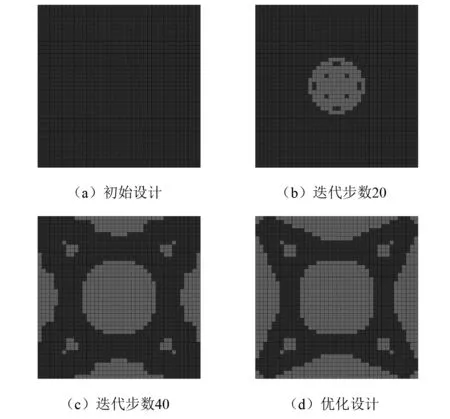
图6 水下强耦合时不同迭代步数下材料的优化分布Fig.6 The optimal distributions at different iteration steps with strong coupling case when the structure immersed in water

图7 优化前后结构z向振动幅值Fig.7 z-direction vibration amplitudes before and after the optimization

为了体现PCLS方法的优越性，我们基于SIMP插值和MMA算法进行了同样的优化设计，优化结果如图8所示。目标函数降到了1.619×10-6m2，高于本文算法的优化值，这同2019年Zhang等研究中的结论保持一致。

图8 MMA算法优化的材料分布Fig.8 The optimal distribution based on MMA method

为了说明耦合条件和环境介质对优化结果的影响，我们又考虑了空气强、弱耦合和水下弱耦合条件。空气强、弱耦合条件下优化结果完全相同，都为图9所示的分布。可以看出，对于空气这类密度相对结构小很多的介质，此时忽略介质对于结构的影响是合理的。弱耦合条件即单向耦合条件，不考虑声场介质对于结构振动的影响，因此水下弱耦合条件时材料的优化结果与空气弱耦合时的相同，即如图9所示。可以看出，水下强耦合条件相对空气强、弱耦合和水下弱耦合条件时强材料在设计域四周的分布存在明显的差异。

图9 空气强、弱耦合与水下弱耦合条件下的材料优化分布Fig.9 The optimal distribution with strong or weak coupling case when the structure immersed in air, or with weak coupling case when the structure immersed in water

为了进一步说明介质为水时，强、弱耦合对于振动响应的影响，图10给出了声场介质为水、初始全为弱材料时，强、弱耦合条件下设计区域z向振幅云图的对比。可以看出，介质为水时强、弱耦合条件下振动响应明显不同，这也说明了介质为水这类相对密度较大的介质时，结构振动响应的计算必须考虑强耦合条件，否则会引起较大的误差甚至计算错误。

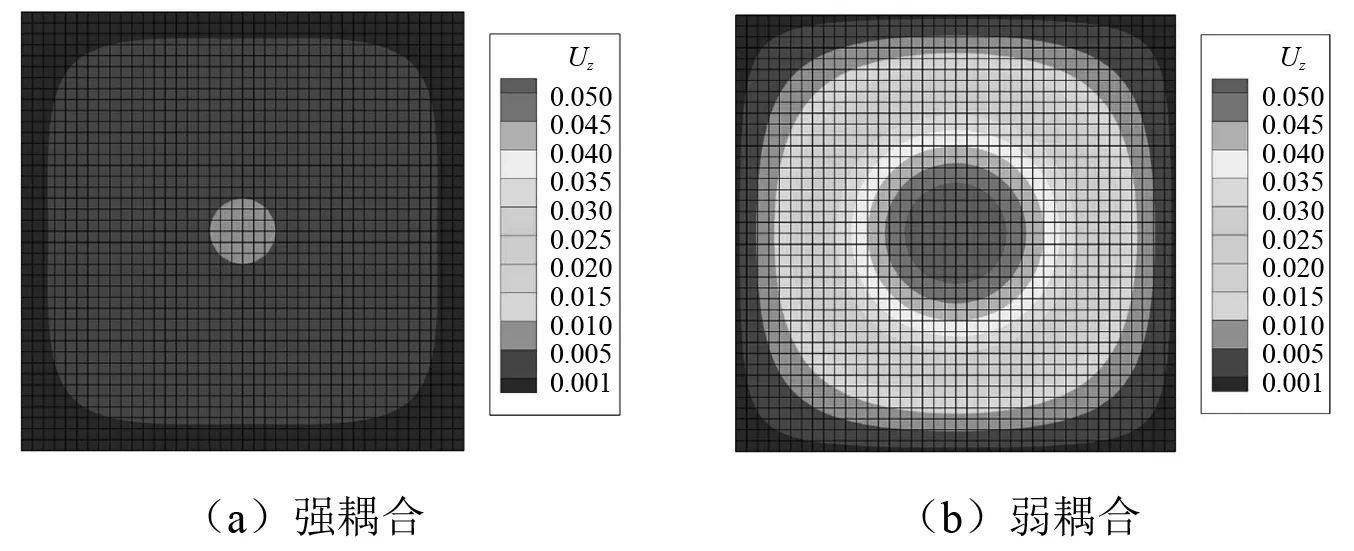
图10 120 Hz水下不同耦合条件时设计域z向振动幅值Fig.10 z-direction vibration amplitudes of design domain with different coupling cases when the structure immersed in water at 120 Hz

针对体积约束参数的问题依赖性，我们将参数按式(40)定义方式同样计算了120 Hz时强耦合的优化结果，设t=1.5,μmax=2×10-7，同本文定义参数的收敛历史对比如图11所示，可以看出，本文提出的参数定义方式优化收敛较快。更重要的是，原参数定义方式会出现参数随算例变化而改变的问题，如在弱耦合时μmax需要设为2×10-5，而本文所有算例的体积约束均在二次罚函数系数取为固定值时得到了很好的满足，说明改进后的方法明显改善了参数的问题依赖性，至少在结构振幅优化的问题中有效，有利于算法的进一步推广。

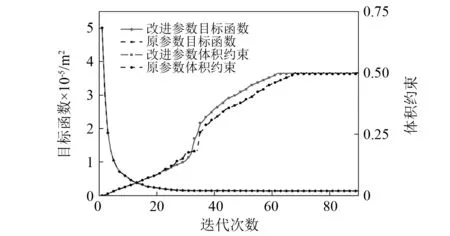
图11 强耦合时参数修改前后收敛历史对比Fig.11 Comparison of convergence histories before and after the parameter modification with strong coupling case

图12给出了不同激励频率下的优化结果。可以明显看出，优化结果随频率变化而变化。在30 Hz时，优化结果较为分散。我们分别对结构为初始设计与优化设计时在30 Hz附近进行了扫频分析，如图13所示。可以发现，当激励频率为30 Hz时，初始设计下结构响应出现了峰值，这可能由于该频率与耦合结构的固有频率较为接近引起的。在优化设计时，结构共振峰频率出现了右移，由30 Hz提高到了47 Hz左右，远离了激励频率，使加载点位移幅值得到大幅降低。同时可以看出，在其他激励频率时优化设计的加载点振幅高于初始设计，说明优化设计只是设计激励频率下的最优设计，不适用于其他频率。

图12 不同激励频率下的材料优化分布Fig.12 The optimal distributions at different excitation frequencies

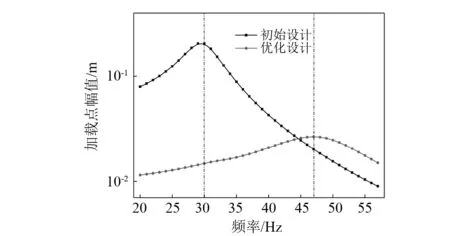
图13 30 Hz附近扫频响应分析Fig.13 Swept-frequency analysis around 30 Hz

当激励频率在60～200 Hz时，随着频率的提高，强材料有向结构中心聚集的趋势。

最后，我们考察了瑞利阻尼系数β对于优化结果的影响，如图14所示。在考察参数修改、强弱耦合条件和介质等因素对于优化结果的影响时，频率设为120 Hz、α设为0.1，因此这里我们将频率固定设为120 Hz、α固定设为0.1。同样可以看出，随着的增大，强材料有向结构中心聚集的趋势。

图14 不同阻尼系数β时的材料优化分布Fig.14 The optimal distributions with different damping coefficents β

6 结 论

本文研究了简谐激励作用下，考虑结构与声场强耦合的水下立方壳体双材料的优化分布问题。采用四节点壳单元和四节点常量元进行结构和声场的离散，基于PCLS方法和瑞利阻尼假设，构造出结构整体刚度阵、质量阵与阻尼阵；目标函数选为结构指定位置处振幅的平方，采用伴随变量方法进行灵敏度计算，降低了计算成本。采用二次罚函数方法使体积约束条件得以满足，对于算法中的体积约束参数进行了重新定义，降低了体积约束参数对问题的依赖性，有利于算法的推广。数值结果表明优化设计可以明显降低结构的振幅，验证了优化方法的有效性。对频率以及瑞利阻尼系数β对于优化结果的影响也进行了进一步的讨论，发现了在计算频段内随频率和β的提高，设计材料呈现向结构中心聚集的趋势。

本文针对的是单个频点时的优化情况，可以进一步考察一个区间内的频段优化问题。