土地利用效率分解、演化与收敛分析
——基于黄河流域69 个城市的实证
薛建春,张安录
(1.内蒙古科技大学 经济与管理学院,内蒙古 包头 014010;2.华中工业大学 公共管理学院,湖北 武汉 430070)
一、引言
土地是城市建设的空间载体,其利用效率直接影响社会、经济的发展以及生态环境的改善[1],随着工业化、城镇化的加速发展,人地矛盾日益突出,黄河流域地处中国西北部,长达5400 多公里流经9 个省份的69 个城市,土地面积接近80 万平方千米,是中国重要的生态屏障区,合理的土地利用方式、高效的土地利用效率可以缓解经济发展产生的土地供需压力,有效推进黄河流域生态保护和经济高质量的协同发展,实现城市“创新、协调、绿色、开放、共享”的发展途径。
关于城市土地利用效率的研究始于20 世纪,学者们最初采用数理方法与地理分析工具从土地集约利用出发,利用容积率、建筑密度、建筑高度等指标评价土地利用效率[2],之后综合评价法、主成分分析法也被广泛使用,1978 年数据包络分析法(Data Envelopment Analysis,DEA)被广泛应用于各类效率评价中,土地利用效率测度从基础研究模型BCC[3]、CCR[4],发展到SBM[5]、Malmquist 指数[6]等,李菁(2017)将非期望产出引入非径向(SBM)模型中,分析了中国31 个省区市和长江中游城市群的城市土地利用效率时空格局及其动态演进[7];黄珂(2014)、吴振华(2016)分别运用三阶段DEA 模型对农地城市流转效率和江浙沪地区城市土地利用经济效率进行测算分析[8,9]。这些方法的使用都为文章寻找测算黄河流域城市土地利用效率提供参考。
很多学者专注于城市土地利用效率与经济增长[10]、土地结构[11]、产业结构[12]之间的关系研究,随着空间模型的推广,城市土地利用空间自相关、空间计量、收敛特性等也成为研究重点[13,14],并在中国省域、长江流域、长江经济带各城市进行了实证分析,但是以黄河流域城市为研究对象的相关文献较少,因此文章选择黄河流域69 个城市为研究对象,采用三阶段Super-SBM-SFA 模型计算城市土地利用效率,采用空间自相关模型与收敛性检验分析城市土地利用效率的空间演进与收敛特性,以期完善国内城市土地利用效率研究的实证应用,同时也为提升黄河流域城市土地利用效率贡献合理政策建议。
二、相关理论模型
1.三阶段Super-SBM-SFA 模型
三阶段非径向Super-SBM-SFA 模型不仅能够破解径向DEA 方法的局限,而且通过在目标函数中引入投入产出松弛量,解除了指标的比例限制要求,还可以区别效率前沿面上为1 的效率值大小,SFA 模型则剔除了环境因素和随机噪声对效率值的影响,思路如下:
(1)构建投入导向Super-SBM 模型计算土地利用初始效率
假设各决策单元(城市)使用m 种投入,q 种产出,则土地利用效率投入用矩阵Xij表示,产出用矩阵Yrj表示,城市土地利用效率可能集为P={(x,yg,yb)|x≥Xλ,yg≤ygλ,gb≥ybλ,1≤eλ≤u,λ≥0},满足约束条件。使用Super-SBM 模型计算效率值时,有效的DMU 单元首先被剔除,度量的超效率值是各DMU 单元到所有无效DMU 单元形成的新生产可能集距离,其规划模型如下:


其中,ρj为评估的效率值,xij、yrj分别为决策单元自身的输入和输出,且q1+q2=q。从公式(1)可以得出,当投入要素的松弛变量较大时,所得效率值则较小;若松弛变量为零值,则ρj=1。将模型(1)在约束(2)的条件下求解n 次,则可以得到城市土地利用效率的过度投入Si-和产出不足Sr+。考虑到规模报酬可变条件下部分Super-SBM模型可能存在无解的可能性,所以选用规模报酬不变条件下基于投入导向的Super-SBM模型计算黄河流域城市土地利用效率值。
(2)采用SFA 回归模型剔除环境因素和随机噪声
随机前沿方法SFA 是效率评价主流的参数法,根据Fried的思想,系统无效率分为管理影响、环境影响和随机误差三种,因此这个阶段利用上一阶段得到的投入变量松弛量,利用选取的环境变量和随机扰动项构造SFA 回归函数,得到剔除环境变量和随机扰动项后的新投入变量:

其中,Sni是第i 个城市第n 项投入的松弛值;Zi是环境变量,βn是环境变量的系数;νni、μni分别表示随机干扰和管理无效率。其中ν 服从正态分布N(0,σν2),表示随机干扰因素对投入松弛变量的影响,μ 表示管理因素对投入松弛变量的影响。
(3)调整投入产出变量后的Super-SBM 土地利用效率最终测度
利用第二阶段得到的新投入产出变量再次采用投入角度Super-SBM模型测算土地利用效率,这时的回归模型中已经剔除了环境控制变量,能够反映土地利用的内生性效率,保证不同决策单元处于相同的环境系统,实现土地利用效率的真实测度。而且由于采用Super-SBM模型测算,无效决策单元不能改变有效生产前沿面,但有效决策单元的生产前沿面发生变化,所以导致测算结果中有效决策单元效率值均大于传统模型的效率测算值。
2.空间相关模型
探索性空间数据分析方法(Exploratory Spatial Data Analysis,ESDA)是将统计学原理与图形图表结合,分析研究区域的空间性质,常用工具有全局空间自相关与局部空间自相关。
(1)全局空间自相关
空间自相关反映了研究区域的空间依赖性,体现了研究对象属性值的相似性与其空间位置属性的一致关系,空间自相关统计指标主要有Moran's I、Geary's、Getis's G 和标准偏差椭圆等,分为空间正相关与空间负相关,正相关表明要素属性值与其相邻空间要素属性值具有相似性,反之亦反。全局Moran's I 指数描述了属性值在整个研究区域的空间特征,计算公式如下[15]:

公式中,xi和yj分别表示不同城市的土地利用效率,且i≠j,表示空间权重的聚合,n 表示研究城市个数。Moran's I 指数的取值范围在[-1,1]之间,其绝对值越接近1 表示在空间上两个单元的相关性越高,指数为正表示两个单元间存在正相关性,指数为负表示两个单元间存在负相关性。
(2)局部空间自相关
局部空间自相关可以进一步解释指标在局部单元内的空间非平衡和一致性特征,局部Moran's I 指数计算公式为:

公式(5)中各值含义与前所述一致,zi和zj表示城市i 和城市j 被标准化后的观测值。局部Moran's I 指数为正值表示该城市及其周围城市均为高值或低值,负值表示该城市与环绕其周围的城市高低值不同。如果I局部>0 且zi>0 表示研究区域i 属于HH 型,I局部>0 且zi<0 表示研究区域i 属于LL 型,若I局部<0 且zi>0 表示研究区域i 属于HL 型,I局部<0 且zi<0 表示研究区域i属于LH 型。
3.收敛性模型
采用收敛模型分析黄河流域城市土地利用效率的收敛性,其中σ 收敛和绝对β 收敛属于绝对收敛模型,条件β 收敛属于局部收敛模型,σ 收敛通常用标准差和变异系数检验,反映指标随时间变化的状况,计算公式如下:

其中,σt、CVt分别表示标准差和变异系数,Yit表示第t 年i 城市的土地利用效率,n 是黄河流域城市总数。若CVt值随时间递减则满足σ 收敛,表明城市土地利用效率的离散程度逐步缩小。
绝对β 收敛主要分析观察变量与变量初期之间的相关关系,其计算公式为:

其中,T 是评价期时间间隔,α,β 分别为变量参数,若β<0,且具有显著性,则认为存在绝对β 收敛,观察变量在评价期间内具有“追赶效应”。
条件β 收敛公式如下:
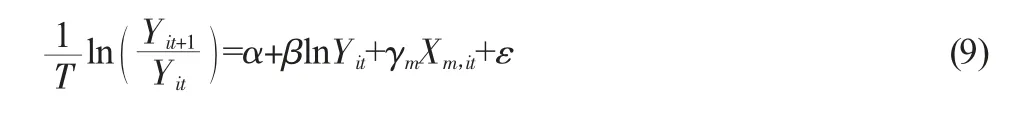
其中,Xm,it为i 城市t 时期第m 个影响因素,γm是变量参数,若β<0,且具有显著性,则认为存在条件β 收敛,观测变量收敛于自身的稳定状态。
三、指标构建与数据来源
1.研究区域概况
根据黄河干流及主要支流流经的城市划定,黄河流域共流经9 各省份的69 个城市,干旱、半干旱的气候造就了流域内的黄土地貌,以及以草地为主的土地利用结构,十八大以后党中央对黄河流域的生态治理提出了更高要求,城市社会、经济、环境的高质量发展要求更高效率的土地利用。流域内69个城市的土地面积约218.3 万平方千米,占国土面积22.74%,GDP 总量130683.18 亿元,占全国经济总量的13.25%,1/4 的土地面积经济总量却不足1/7[16];同时,资源环境的胁迫效应对流域内城市土地利用的约束日益凸显,城市内部资源禀赋、产业结构的差异也为提高土地利用效率带来严峻挑战[17],土地利用效率低下成为黄河流域生态保护和高质量发展的瓶颈。
2.指标构建及说明
考虑到城市土地利用碳排放对城市土地利用效率的约束性,测度指标选用如表1,其中生态效益指标土地利用碳排放量是非期望产出,所有价值类指标利用GDP 指数平减至2009年为基期的数值。环境变量选取短时期内无法对其有效控制,但影响土地利用效率的常住人口、水域及水利设施用地面积两个指标。
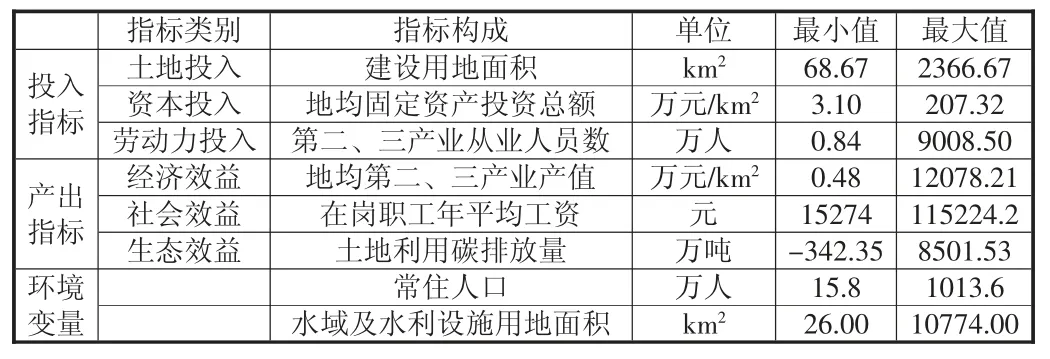
表1 城市土地利用效率投入-产出指标
城市土地利用碳排放量的测算主要包含建设用地、耕地、园地、林地、草地、水域和其他未利用地类,为了简化计算,建设用地碳排放量使用城市能源消费量作为基础数据,根据能源消耗总量与每吨标准煤综合碳排放系数的乘积计入,这里的能源类型主要包含煤炭、焦炭、石油、原油、汽油、煤油、柴油、燃料油、液化石油气和天然气10 种,每吨标准煤的碳排放系数以赵荣钦等(2013)[18]学者对各类能源碳排放系数的计算结果作为参数值(表2),通过计算研究区域各年的能源消耗碳排放系数,最终确定研究区域每年每吨标准煤综合碳排放系数为0.74t/t 标准煤。

表2 不同类型能源、土地碳排放系数
3.数据来源
效率测度所需的投入、产出变量及环境变量数据均来源于WIND 数据库中黄河流域各城市的《城市统计年鉴》,以及《能源统计年鉴》和城市土地利用变化数据,由于MaxDEA 要求测度数据完整,缺失数据查询地方官网的政府工作报告或者利用插值法补入,个别城市无在岗职工年平均工资采用城镇职工年平均工资代替,研究时段选取2009—2018 年。
四、结果分析
1.城市土地利用效率分解分析
利用MaxDEA 软件,选择基于投入角度、规模报酬不变、Super-SBM模型测算投入指标松弛值,利用SFA 方法以常住人口、水域及水利设施用地面积作为环境变量调整投入指标的松弛值,再次运用Super-SBM模型得到黄河流域的城市土地利用效率值(LUE),结果如表3 所示,进一步分解为纯技术效率(PTE)、规模效率(SE)和混合效率值(MIX)。
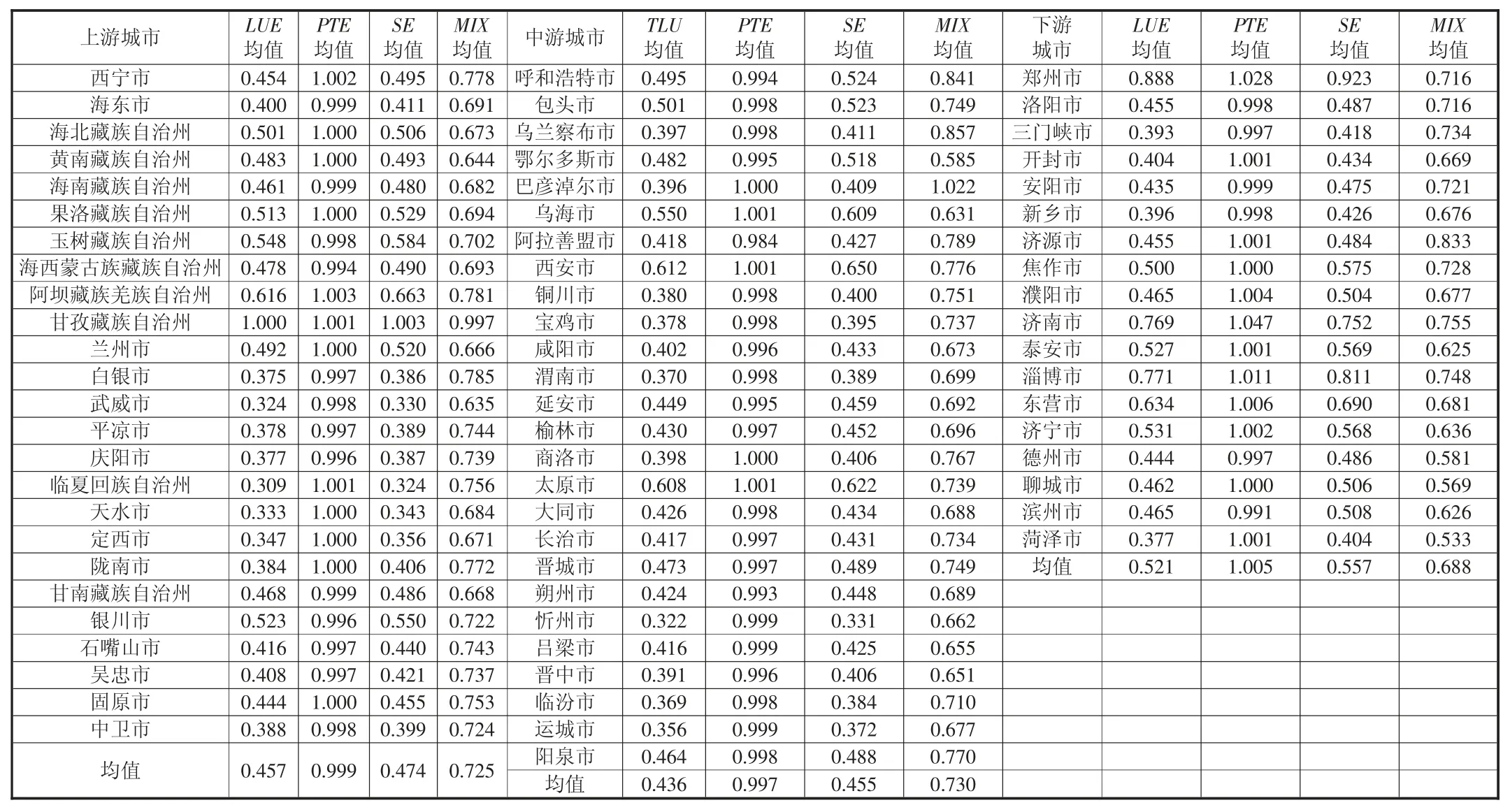
表3 2009—2018 年黄河流域城市土地利用效率均值及分解
整体而言,黄河流域各城市的土地利用效率值较长江流域、珠江流域偏低,10 年间69 个城市的土地利用效率均值0.465,且流域内下游水平(0.520)高于上游(0.458)和中游(0.440),这主要是由于下游城市的土地利用开发较多,建设用地面积、二、三产业从业人数、地均固定资产投资额都要高于上游和中游,且地均经济产值也相对较高。从所属省域看,甘肃、山西、陕西的沿黄城市土地利用效率均值较低。
虽然黄河流域所有城市土地利用效率逐年递增,但是截至2018 年仅有海北藏族自治州、甘孜藏族自治州、郑州市、济南市、淄博市5 个城市的效率值大于1,说明流域内城市土地利用效率仍然存在较大提升空间。进一步观察发现,各省会城市的利用效率相对较高,这是由于各类生产要素投入产出集中在省会城市,且省会城市是城市社会、经济发展的核心,对周边城市发展具有“虹吸效应”,导致距离省会城市较远的城市土地利用起步较晚、发展缓慢。此外,一些耕地、草地、林地面积占比较大的城市其利用效率也相对较高,例如甘孜藏族自治州和海北藏族自治州,这是因为文章研究的土地利用效率测度是包含非期望产出的超效率值,而这些城市的碳汇用地面积相对较大,重工业生产与生态破坏较小,因此土地利用效率值也相对较大。这也为中游城市进一步提高土地利用效率提供了一种思路,可以通过降低非期望产出达到提升土地利用效率的目的,但是非期望产出指标与产业结构、建设用地投入息息相关,因此中游城市需要通过优化产业结构,降低能耗、减少资源浪费与建设用地的投入,提升土地利用效率。
分析各城市的纯技术效率变化:下游(1.005)>上游(0.999)>中游(0.997),变化区间0.983~1.443,上、中、下游三个流域的纯技术效率值普遍偏高且水平相近,2018 年纯技术效率值大于1 的城市有34 个,济南市增长最多(0.440),焦作市下降最多(0.012)。
分析各城市的平均规模效率:下游(0.557)>上游(0.474)>中游(0.455),变化区间0.324~1.003,虽然大部分城市呈现递增趋势,但2018 年仅3 个城市的规模效率大于1。从所属省域看,山东省9 个城市的规模效率平均值最高0.588,甘肃省的规模效率平均值最低0.393。说明黄河流域各城市的土地利用规模和管理效果差异较大,部分城市的土地利用效率投入与产出结构不合理,管理效率低下,同时也说明规模效应是造成土地利用效率差异的主要原因。
为了更详细地分析城市之间土地利用效率差异,文章依据地均GDP 指标将黄河流域9 个省份的69 个城市划分为三类城市(表4)。

表4 黄河流域城市分类标准
按照以上分类依据得到的各类型城市中,土地利用效率差异明显,总体上表现的规律为:高速发展类(0.552)>低速发展类(0.516)>中速发展类(0.398),可见地均GDP 的提高与土地利用效率不存在完全正相关关系。纯技术效率整体处于较高水平,对土地利用效率的贡献率较大,而且高速发展类城市呈现快速增长的发展趋势,中速发展类城市呈现“U”型增长趋势,低速发展类城市呈现上下波动的趋势。这表明黄河流域城市土地利用效率与其产业路径依赖程度存在直接关系,高、中速发展类城市的管理、技术水平与其地均GDP 发展水平相匹配。规模效率总体的表现规律为:高速发展类(0.524)>低速发展类(0.518)>中速发展类(0.401),而且各类城市的规模效率呈现平稳上升趋势,说明黄河流域内城市产业规模在研究期间内也是平稳增长的趋势。
2.城市土地利用效率空间演化分析
为了更好地呈现黄河流域各城市之间的土地利用效率增长差异,突出空间差异特征,利用GeoDA 空间分析软件,测算得出2009—2018 年黄河流域城市土地利用效率的全局Moran's I指数如表5 和图1 所示。

图1 黄河流域不同分类城市土地利用效率分解变化
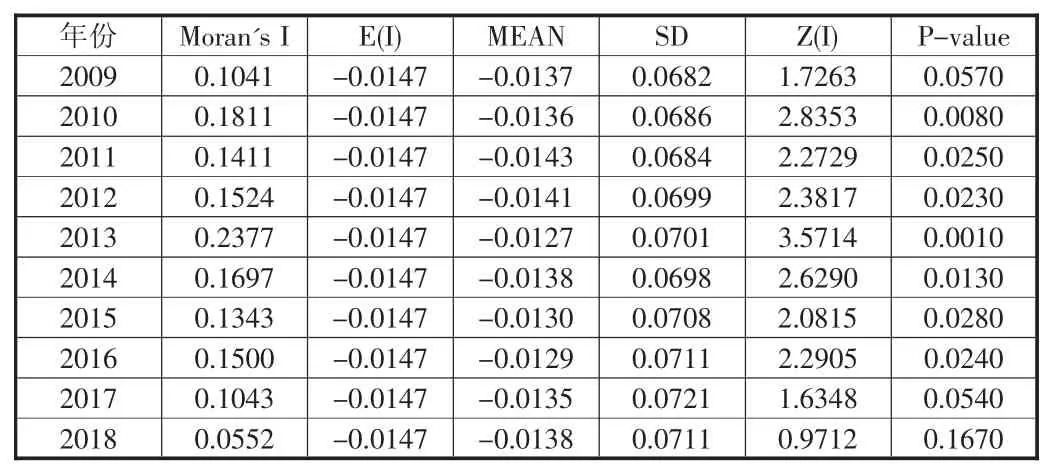
表5 黄河流域城市土地利用效率全局Moran's I 指数
可以发现,除2018 年以外,黄河流域内城市的土地利用效率Moran's I 指数均在5%水平显著,而且显示为正值,表明69 个城市之间存在邻近正效应,或者说具有空间溢出性,即某个城市的土地利用效率不仅会影响邻近城市的土地利用效率,而且自身也会受邻近城市的影响。由于Moran's I 指数的变化区间较小,说明整个流域内强弱交替变化特征不明显,全局空间相关性基本形成稳定状态。
再观察局部Moran's I 指数散点图和LISA 集聚图,如图2所示,Moran's I 指数散点图以笛卡尔指数坐标系表示,横坐标是标准化后的各城市土地利用效率值,纵坐标是邻接空间权重矩阵决定的相邻城市土地利用效率均值。可以发现2009 年局部Moran's I 指数在5%水平下显著的城市有8 个,其中,处于低-低区域的有5 个城市,分别为天水市、平凉市、固原市、定西市、临夏回族自治州,处于高-高区域的有3 个,分别为果洛藏族自治州、玉树藏族自治州、阿坝藏族羌族自治州,说明2009 年黄河流域内城市的土地利用效率普遍偏低,且上游城市的土地利用效率相对较高。2018 年局部Moran's I 指数在5%水平下显著的城市有12 个,处于高-高区域的只有淄博市,处于低-低区域的城市增长为6 个,分别是榆林市、延安市、临汾市、运城市、三门峡市和平凉市。低-高区域城市为海西蒙古族藏族自治州、开封市和滨州市,高-低区域城市分别为西安市和太原市。说明经过10 年的发展,部分低-低区域内城市已经提高了土地利用效率,但平凉市一直处于低效率阶段;同期,省会城市的土地利用效率提高较快,但其周边城市的土地利用效率依然较低。结合前面分析得到的空间溢出性,省会城市的高效土地利用结果会溢出影响周边城市的土地利用。

图2 2009 年和2018 年城市土地利用效率局部Moran's I 指数散点图
3.城市土地利用效率收敛性分析
(1)σ 收敛分析
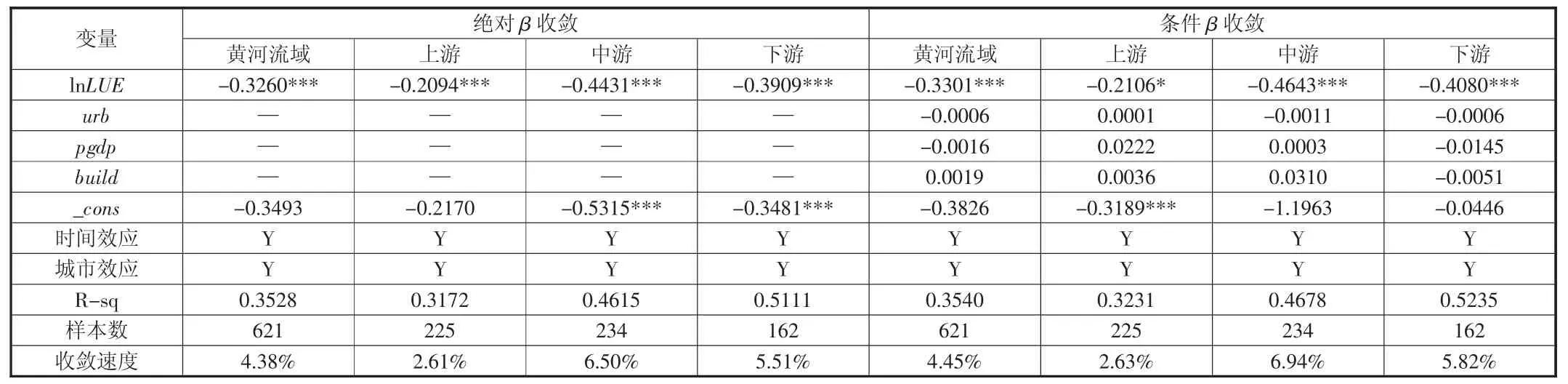
如图3 所示,分析流域内城市土地利用效率值的收敛特性,可以发现随着时间的推进,黄河流域各年土地利用效率的变异系数呈现整体下降趋势,特别是2011—2016 年下降趋势更明显,而且上、中、下游各区域的城市土地利用效率变异系数也存在CVt+1 图3 黄河流域及其上、中、下游2009—2018 年土地利用效率的σ 收敛性 (2)β 收敛分析 σ 收敛侧重于城市土地利用效率值的横向比较,而β 收敛则更注重研究对象的纵向比较,如果存在绝对β 收敛,表明土地利用效率低的城市其增长率要高于土地利用效率值高的城市增长率,收敛速度利用公式ν=-ln(1+β)/T 计算。 利用公式(8)分析69 个城市土地利用效率的绝对β 收敛性(表6)。结果显示,黄河流域全域及上、中、下游的土地利用效率均通过了t 检验,且在1%水平显著,β 系数均为负,表明流域内各城市土地利用效率存在绝对β 收敛,即城市之间具有“追赶效应”。 为了验证土地利用效率的条件收敛性,选择城镇化率、人均GDP 和建设用地占比三个指标作为控制变量,其中城镇化率选用非农人口数与常住人口数比值表示,建设用地占比选用全市建设用地面积占城市行政区划面积表示。由于各城市拥有不同的初始水平,所以其收敛的不同稳态水平也会存在差距,因此利用公式(9)选择时间个体双向固定效应模型进行检验(表6)。结果显示,增加了控制变量以后,条件收敛模型下所有城市的土地利用效率值也显著通过t 检验,且回归系数均为负值,说明黄河流域各城市都朝着各自的稳态水平趋近,而且条件收敛的β 系数普遍大于绝对收敛的β 系数,平均收敛速度:中游>下游>上游,同一流域内条件收敛下的平均收敛速度也都大于绝对收敛下的平均收敛速度,模型的收敛性增强。 表6 评价期间土地利用效率的β 收敛检验结果 借助三阶段Super-SBM-SFA 模型剔除了人口、水域环境变量对黄河流域城市土地利用效率的影响后,得到更为客观的城市土地利用效率值,进一步分解效率值,分析其时序变化、空间自相关性和收敛特性。 第一,研究区间内,黄河流域69 个城市的土地利用效率均值0.465,总体水平较低,且下游>上游>中游,但各城市的土地利用效率呈现逐年增长趋势,平均增速3.825%;纯技术效率值普遍较高,规模效应是影响城市土地利用效率的主要因素;2018 年仅5 个城市的土地利用效率值大于1,且8 个省会城市的土地利用效率值相对较高,城市土地利用效率不存在完全的经济规模等级递增效应,中速发展类城市的土地利用效率最低,建议黄河流域各城市积极提升城市土地利用效率时不简单考虑经济效益,不盲目扩大城市规模,应该合理配置土地生产要素,因地制宜开发利用土地,积极推进高科技成果在土地利用过程中的成果转化,依靠创新技术走高质量发展道路。 第二,通过自相关分析得出,黄河流域69 个城市之间存在邻近正效应,整个流域内强弱交替变化特征不明显,经过10年发展,部分低-低区域的城市提高了土地利用效率,而高-高区域的城市却进入低-高或高低区域;大部分省会城市率先进入高效土地利用阶段,建议各省会城市积极发挥辐射带动作用,带领邻近城市通过人才投入、资本投入、科技投入等方式,同时兼顾碳排放量的负向制约,有效提升城市土地利用效率。 第三,黄河流域及其上、中、下游均存在σ 收敛性,各城市土地利用效率值的离散程度呈现逐年缩小态势,不同流域内城市土地利用效率具有“追赶效应”,存在绝对β 收敛性和条件β 收敛性,而且条件收敛的β 系数普遍大于绝对收敛的β 系数,同一流域内条件收敛下的平均收敛速度大于绝对收敛下的平均收敛速度,体现了模型的收敛性增强。建议黄河流域及其上、中、下游内部各城市之间加强互鉴和学习,在提升各自城市土地利用效率的同时缩短收敛时间,达到流域内的协同发展。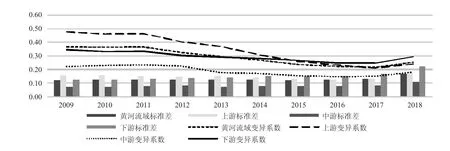
五、结论与建议

