Soliton fusion and fission for the high-order coupled nonlinear Schrdinger system in fiber lasers

Tian-Yi Wang(王天一), Qin Zhou(周勤), and Wen-Jun Liu(刘文军),†

1State Key Laboratory of Information Photonics and Optical Communications,School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

2Mathematical Modeling and Applied Computation(MMAC)Research Group,Department of Mathematics,King Abdulaziz University,Jeddah 21589,Saudi Arabia

With the rapid development of communication technology, optical fiber communication has become a key research area in communications.When there are two signals in the optical fiber, the transmission of them can be abstracted as a high-order coupled nonlinear Schrdinger system.In this paper, by using the Hirota’s method, we construct the bilinear forms, and study the analytical solution of three solitons in the case of focusing interactions.In addition, by adjusting different wave numbers for phase control,we further discuss the influence of wave numbers on soliton transmissions.It is verified that wave numbers k11,k21,k31,k22,and k32 can control the fusion and fission of solitons.The results are beneficial to the study of all-optical switches and fiber lasers in nonlinear optics.

Keywords: soliton,Hirota’s method,high-order coupled nonlinear Schrdinger system,soliton transmission

1.Introduction

Solitons exist in such physical fields as plasma, nonlinear optics, Bose–Einstein condensation, and so on.[1–7]They play an important part of nonlinear science,which are widely studied and applied in optical fiber systems.[8–14]Solitons can realize stable transmission in long distance signal transmission by monitoring the equilibrium between group velocity dispersion(GVD)and self-phase modulation(SPM).[13,15]When the pulse duration is in picosecond range,the fiber pulse transmission includes the GVD and SPM terms.This process can be described by the nonlinear Schrdinger (NLS)equation.However, some additional high-order effects need to be considered when we consider ultrashort fiber pulses with pulse duration in the range of sub-picosecond and femtosecond.Those high-order effects include stimulated Raman scattering, self-steepening, and third-order dispersion effects.[16–24]On the other hand, in optical fiber communications, the NLS equation can only describe pulse transmission in single-mode fibers.[11,15]For birefringent fibers, it is usually necessary to use coupled NLS equations to describe their transmission.[11,15,25]The solitons corresponding to this kind of system are called vector solitons,which are not completely equivalent to scalar soliton.[15,26–28]Therefore, the study of vector solitons has attracted the attention of researchers.[26–30]

Solitons can be transmitted lossless under ideal conditions.[31]However, when there are multiple solitons in optical fibers at the same time, the solitons will interact with each other.[31–33]This will affect the transmission effect of optical communications,so it is of great significance to study the interactions between solitons.[34,35]At present,there have been some research results on the two soliton solutions of coupled NLS systems,but the properties of three soliton solutions are still poorly understood.Phase shift control is a widely used method in various researches and experiments for soliton interactions.[36,37]

In this paper, we use a high-order coupled NLS(CNLS)system to describe the transmission of three solitons in birefringent fibers,[38–41]

Here,q1andq2represent the soliton intensities,the subscriptxis the partial differential derivative in space,andtis the partial differential derivative in time.We denote the complex conjugate by the symbol “∗”, and δ is a real small parameter, which represents the magnitude of the higher-order effects.For convenience, we suppose that σ1=σ2=1, which denotes focusing interactions.In this case, it is worth noting that the Darboux transformation has been used in the area of vector semi-rational rogue waves and got some useful results.[38]Breathers and dark–bright semi-rational solitons in high-order CNLS systems in optical fibers have been studied.[39]Akhmediev breather,Kuznetsov–Ma breather,and rogue-wave solutions for Eq.(1) have been obtained via the Darboux transformation.[40]Certain Lax-integrable properties and bright–bright soliton solutions for Eq.(1) have been reported via the Riemann–Hilbert formulation.[41]

The transmission phenomena of three soliton interactions are rich and varied,which are different from the clear and intuitive phenomena of two soliton interactions.Using the method of phase shift control and setting the appropriate wave numbers, we can get some three-soliton transmission phenomena with obvious characteristics,and then analyze the interactions under different parameters.Besides, by changing the constraint values generated byk11,k21,k31,k22, andk32, the fusion and fission of solitons can be effectively presented,so as to obtain better transmission effect.This can improve the signal transmission effect of the optical communication system,achieve better signal transmission,and enhance the stability of the system.

The rest of this paper is arranged as follows.In Section 2,by using Hirota’s method,we will solve the three soliton solutions of Eq.(1).In Section 3,the interaction effects of different parameters are analyzed and the appropriate values to adjust the interactions among the three solitons are found.Finally,Section 4 is the conclusion of this paper.

2.Bilinear forms and three solitions of the system

In this paper, we only discuss the case of σ1=σ2=1.Using the dependent variable transformation derived from the Hirota’s method,we have[42]

wheref(x,t)is a real differentiable function whileh(x,t)andg(x,t) are complex.We can get the bilinear equations of Eq.(1)as follows:[42,43]

As Hirota bilinear operators,DxandDthave the following forms:[42]

Here,mandnare both positive integers, anda(x,t) is the differentiable function aboutxandt.Similarly,b(x,t) is the differentiable function aboutx′andt′.h(x,t) andf(x,t) can be expanded as the following expressions based on bilinear forms(3):

In gengeral,we can construct three solitons with the value of parameter ε taken as 1.Then by substituting Eq.(5)into the bilinear forms(3),we can get the following formluas:

where

Supposing σ1=σ2, by substituting expressions (7)–(9)into expressions (6), and then into expressions (3), the coefficients before then-th power of ε are extracted respectively and made to be 0.The following results can be obtained by solving the equations respectively:

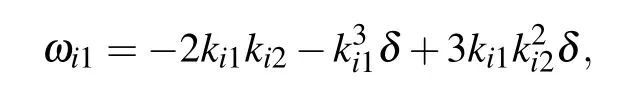
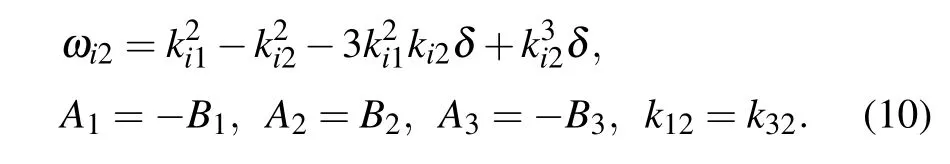
Here,AiandBiare real numbers(i=1,2,3).

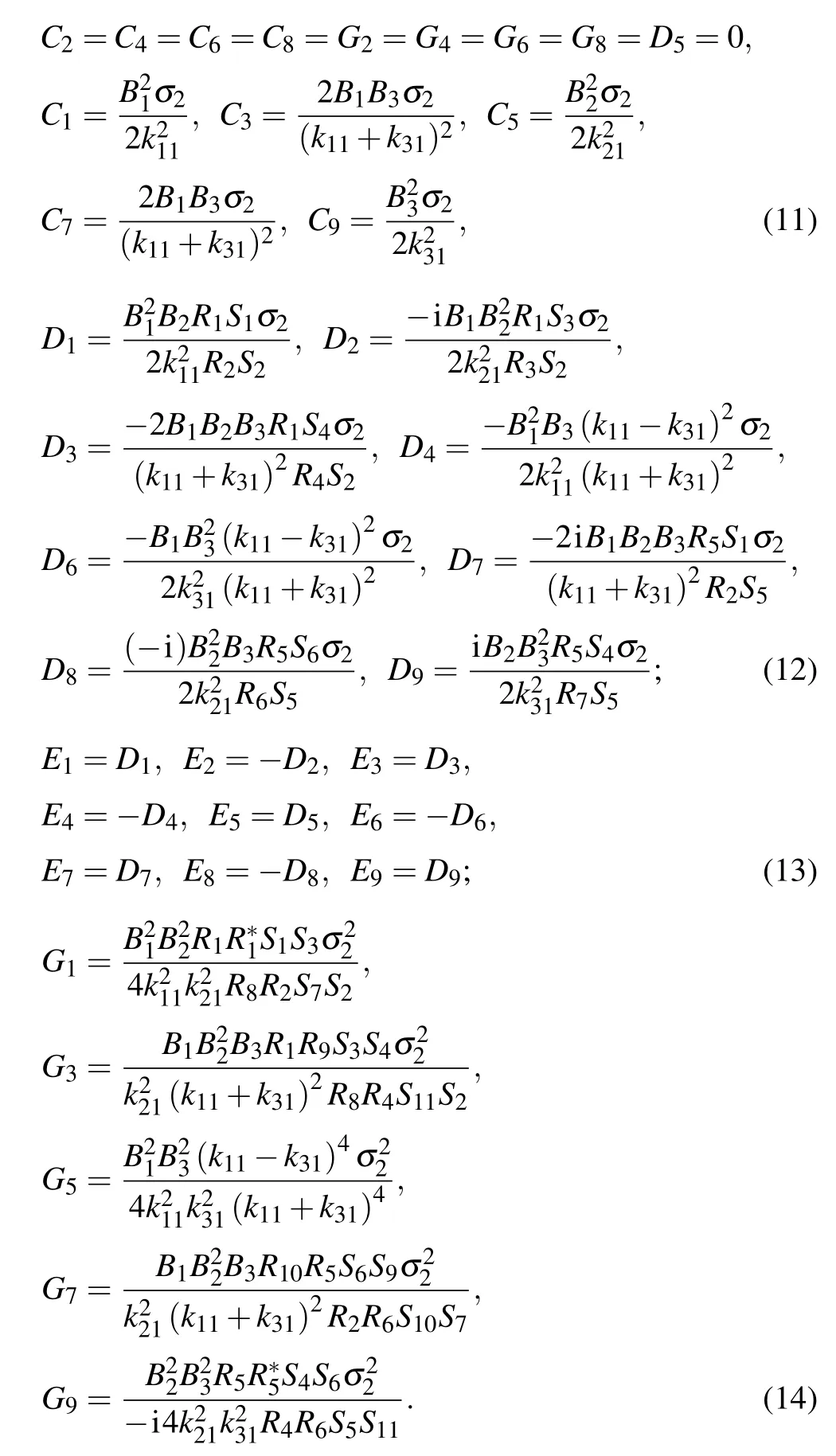
Here,RiandSican express as follows:

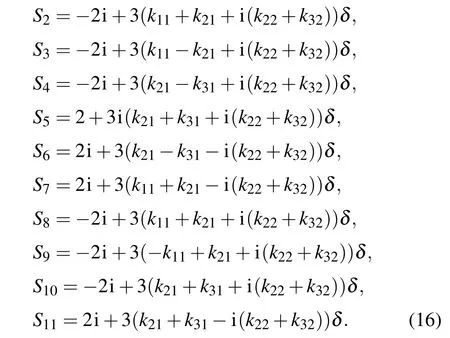
Similarly,

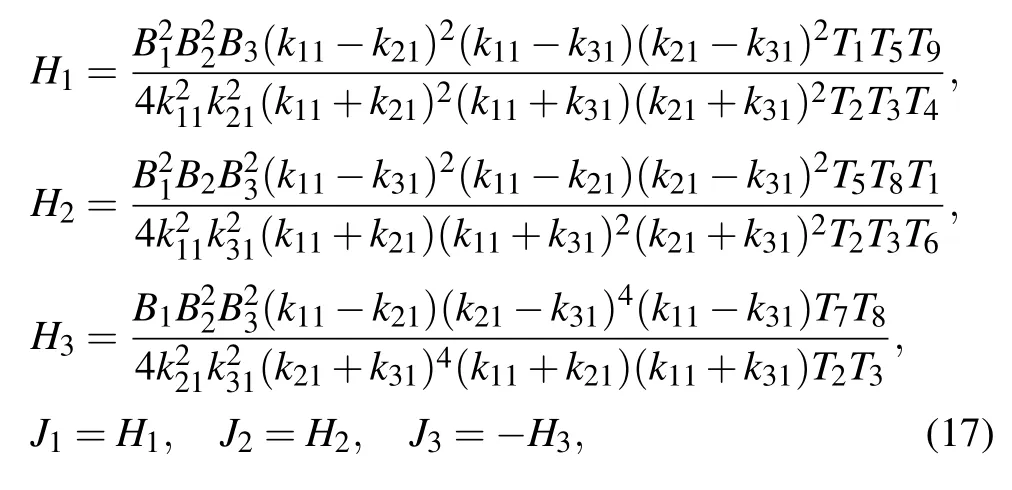
where

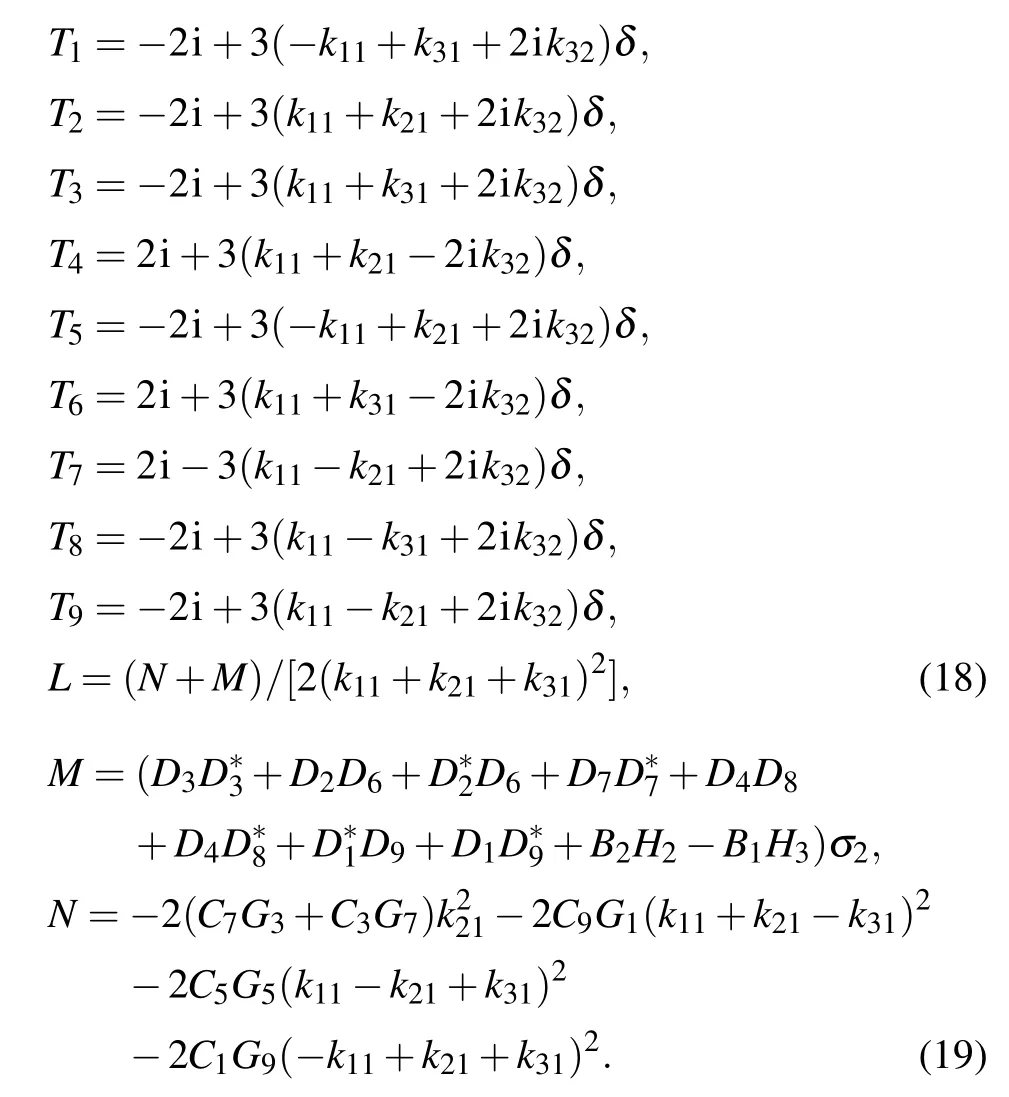
3.Discussion

For solutions (7) and (8), by choosing different wave numbers, that is, the values ofk11,k21,k31,k22, andk32, we may obtain the solutions of three solitons and investigate the interactions between them.Then, we can analyze the interaction behavior in different wave numbers.By adjusting the parameters,we can observe the interaction properties of three solitons.In addition, in the process of adjusting the parameters,we can find that some novel nonlinear phenomena can be induced by the higher-order effects.Figures 1–4 demonstrate the interactions among three solitons with different constantsk11,k21,k31,k22,andk32.Among them,figures 2–4 show the solitons fusion and fission,which are caused by the high-order effects.

From Fig.1(a), whenk11=−1.6,k21=2.2,k22=0.7,k31=2.3,andk32=1.3,we can see that at this time,two solitons are completely parallel, and the amplitude is very close.At the same time, one soliton forms an acute angle with the other two solitons and interacts with two solitons.The interaction at one intersection is not obvious, which indicates that the two solitons are incompatible in the image,while the other intersection reflects the interaction between the two solitons.There is a significant increase in the amplitude of the soliton at the intersection, which reflects the energy superposition of the two solitons.

Fig.1.The interaction characteristics among three solitons.Parameters are chosen as(a)k11 =−1.6, k21 =2.2, k22 =0.7, k31 =2.3, k32 =1.3, ξ11 =−2.5, ξ12 =−1, ξ21 =2.3, ξ22 =1.3, ξ31 =−1.9, ξ32 =2.9, B1 =−0.47,B2 =1.1, B3 =−2.8, δ =0.05, σ =1.(b) k11 =−1.6, k21 =1.3, k22 =−0.11, k31 =2.3, k32 =1.3, ξ11 =−2.5, ξ12 =−1, ξ21 =2.3, ξ22 =1.3,ξ31=−1.9,ξ32=2.9,B1=−0.47,B2=1.1,B3=−2.8,δ =0.05,σ =1.

However, when the values of other variables remain unchanged,k21andk22are taken as smaller values 1.3 and−0.11, respectively, we can observe from Fig.1(b) that the direction and amplitude of the two solitons remain unchanged and keeping parallel,while the direction of the solitons intersecting with them changes significantly.It makes the angle between the soliton and two parallel solitons larger and closer to perpendicular.At the same time,the amplitude of the soliton decreases and the width increases.This means that the energy of the soliton also changes.At the intersection point,two parallel soliton directions bend because of the intersection,and the amplitude increases because of the superposition of the energy.From Fig.1, we can conclude thatk21andk22control the soliton fusion and fission.Meanwhile, the intersection points of the two cases are slightly different due to the change ofk21andk22.

Readjust the values ofk11,k21,k31,k22, andk32, other parameters remain unchanged.Letk11= −1,k21= −1.7,k31=2.0, andk22=k32=0.Here, due to the previous assumption(k12=k32),the imaginary parts of the solution are all equal to 0.We can get a special result,as shown in Fig.2(a).On the right side of the graph,we can see three solitons transmitted in different directions.After simultaneous interpreting, the left side is a soliton form.The whole looks like a broom.As can be seen in Fig.2(a),almost the same amplitude in the lower left corner of three soliton–soliton amplitudes is keeping to the upper right corner,there is no abnormally high amplitude, which means that the energy represented by solitons is not superimposed,indicating that soliton is not formed by three of aggregations.Because the phase of the soliton changes and the transmission direction remains unchanged after the interaction, we can see that the right soliton and the lowest soliton on the left are the same soliton solution, while the other two solitons disappear after they intersect.In aspect of amplitude,the amplitudes of the three solitons on the right increase at one time,the amplitudes of the top soliton are the smallest,and those of the bottom soliton are the largest.When we change the values ofk11,k21, andk31to positive values,that is,k11=1,k21=1.7,andk31=2.0,and other parameters remain unchanged,as shown in Fig.2(b),we get the result of soliton propagation in the opposite direction.In addition, the transmission direction of the soliton has also changed,not only in the horizontal direction,but also in the vertical direction.In Fig.2(a), there is a soliton form on the left, which is modulated.After integration,it becomes a soliton on the right side and three solitons on the left side, and the amplitude of the three solitons gradually decreases from top to bottom.This shows that the parametersk11,k21,andk31control the soliton fusion and fission.

Fig.2.The interaction characteristics among three solitons.Parameters are chosen as(a)k11 =−1,k21 =1.7,k22 =0,k31 =2.0,k32 =0,ξ11 =−2.5,ξ12=−1,ξ21=2.3,ξ22=1.3,ξ31=−1.9,ξ32=2.9,B1=−0.47,B2=1.1,B3=−2.8,δ =0.05,σ =1.(b)k11=1,k21=−1.7,k22=0,k31=−2.0,k32=0,ξ11=−2.5,ξ12=−1,ξ21=2.3,ξ22=1.3,ξ31=−1.9,ξ32=2.9,B1=−0.47,B2=1.1,B3=−2.8,δ =0.05,σ =1.

Keeping other parameters unchanged,changing the value ofk11from −1 to −0.62,we can get Fig.3(a).Compared with Fig.2(a), we can see that the change ofk11leads to obvious changes in the transmission direction and shape of the uppermost soliton.The uppermost soliton is more upward shifted with smaller amplitude and lower energy,and the intersection of the three solitons is also shifted to the left.This shows that the modulation ofk11can control the propagation angle and amplitude of one soliton in the triple soliton solution.The right soliton still keeps an angle with the lowest soliton on the left.Changing the sign ofk11,k21,andk31can get the image with opposite soliton transmission direction,as shown in Fig.3(b).we can see more clearly that the transmission form of the soliton has changed 180°compared with that in Fig.3(a).

Fig.3.The interaction characteristics among three solitons.Parameters are chosen as(a)k11=−0.62,k21=1.7,k22=0,k31=2.0,k32=0,ξ11=−2.5,ξ12=−1,ξ21=2.3,ξ22=1.3,ξ31=−1.9,ξ32=2.9,B1=−0.47,B2=1.1,B3=−2.8,δ =0.05,σ=1.(b)k11=0.62,k21=−1.7,k22=0,k31=−2.0,k32=0,ξ11=−2.5,ξ12=−1,ξ21=2.3,ξ22=1.3,ξ31=−1.9,ξ32=2.9,B1=−0.47,B2=1.1,B3=−2.8,δ =0.05,σ =1.

On the basis of Fig.3,adjustingk11,k21to −1.8,1.9,k31to 2.0, we can get a new group of images in Fig.4(a).From Fig.4(a),we can more clearly see that the following two solitons disappear in the transmission.The soliton morphology is slightly different from that in Figs.2 and 3.The shape of the three solitons also changes from flat to wavy.The only soliton with constant energy is the one at the top.There is no obvious interaction among the three solitons.By changing the sign ofk11,k21, andk31, we can also get the soliton propagation direction opposite to Fig.4(b).

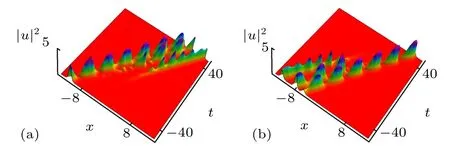
Fig.4.The interaction characteristics among three solitons.Parameters are chosen as(a)k11=−1.8,k21=1.9,k22=0,k31=2.0,k32=0,ξ11=−2.5,ξ12=−1,ξ21=2.3,ξ22=1.3,ξ31=−1.9,ξ32=2.9,B1=−0.47,B2=1.1,B3=−2.8,δ =0.05,σ =1.(b)k11=1.8,k21=−1.9,k22=0,k31=−2.0,k32=0,ξ11=−2.5,ξ12=−1,ξ21=2.3,ξ22=1.3,ξ31=−1.9,ξ32=2.9,B1=−0.47,B2=1.1,B3=−2.8,δ =0.05,σ =1.

4.Conclusion

By using the Hirota method, we have constructed the three-soliton solutions of the high-order CNLS system.When choosing different wave numbersk11,k21,k31,k22, andk32,we have obtained different soliton interactions and shapes,and soliton fusion and fission have been observed.When the imaginary parts of wave numbers are equal to 0,we have obtained the splitting of solitons by controlling the phase, and have changed the solitons’propagation direction by controlling the values of the real part.In addition, we can adjust the propagation direction and amplitude of one of the three solitons and the interaction form of the two solitons by controlling the values of the real part of wave numbers.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.11875008, 12075034,11975001, and 11975172), the Open Research Fund of State Key Laboratory of Pulsed Power Laser Technology (Grant No.SKL2018KF04),and the Fundamental Research Funds for the Central Universities,China(Grant No.2019XD-A09-3).