Collective behavior of cortico-thalamic circuits: Logic gates as the thalamus and a dynamical neuronal network as the cortex

Alireza Bahramian Sajjad Shaukat Jamal Fatemeh Parastesh Kartikeyan Rajagopal and Sajad Jafari

1Department of Biomedical Engineering,Amirkabir University of Technology(Tehran polytechnic),Iran

2Department of Mathematics,College of Science,King Khalid University,Abha,Saudi Arabia

3Centre for Nonlinear Systems,Chennai Institute of Technology,Chennai,India

4Health Technology Research Institute,Amirkabir University of Technology(Tehran polytechnic),Iran

This paper introduces a two-layer network to investigate the effects of cortico-thalamic circuits on the cortex’s collective behavior. In the brain,different parts of the cortex collaborate to process information. One of the main parts,which is the path of different cortex contacts,is the thalamus whose circuit is referred to as the“vertical”cortico-thalamic connectivity. Thalamus subnuclei can participate in the processing of the information that passes through them. It has been shown that they play the functional role of logic gates(AND,OR and XOR).To study how these thalamus circuits affect the cortical neuron behavior,a two-layer network is proposed wherein the cortex layer is composed of Hindmarsh–Rose models and the thalamus layer is constructed with logic gates. Results show that considering these logic gates can lead the network towards different synchronization, asynchronization, chimera and solitary patterns. It is revealed that for AND-gate and OR-gate,increasing the number of gates or their outputs can increase and decrease the network’s coherency in excitatory and inhibitory cases,respectively. However,considering XOR-gates always results in the chimera state.

Keywords: two-layer network,synchronization,chimera state,thalamus and cortex

1. Introduction

To comprehend the mechanism of complex behavior in the brain, it is necessary to pay attention to complexity science[1,2]and use its mathematical methods. One of the computational tools for modeling complex systems such as the brain is a multi-layer network.[3]This framework allows one to study the interactions of different parts of the brain.[4,5]Investigation on how different parts of the brain influence each other can help one to understand how the brain works.[4]The cortex is anatomically the outermost layer of the mammalian brain.Cognitive functions and most of the information processing in the brain are carried out by the cortex when different parts of the cortex interact with each other to do tasks.[6]Different regions of the cortex are connected to each other through direct connections referred to as “horizontal” cortico-cortical connectivity or through the thalamus,referred to as“vertical”cortico-thalamic connectivity[7](Fig.1).

The thalamus is paired gray matter mass on both sides of the brain, located higher than the midbrain. Thalamus fibers are projected to all sides of the cortex.[8]Most sensory inputs are sent through the thalamus to different parts of the cortex. Therefore, the role of the thalamus as a relay is prominent.[8]Thalamus cells are not just simple relays but actively update the different cortex parts from newly received information.[9]In addition, thalamus neurons in “vertical”cortico-thalamic connectivity participate in connecting different regions of the cortex.[10]These cortico-thalamic circuits play a crucial role in the regulation of human wakefulnesssleep circulation.[11]Thalamus nuclei that participate in these circuits are not only simple relays,and participate in the processing of information.[12]For instance, it has been shown that its posteromedial complex nuclei (POM) can act as the logic gates like AND-gate and OR-gate.[13]POM cells are inhibited by their nearby neuron zona incerta (ZI).[14]When these ZI inhibitions are strong, POM act in a similar way to the AND-gate.[15]On the other hand, when these ZI inhibitions are light, they function like the OR-gate.[15]Furthermore, it has been experimentally[16]and computationally[17]revealed that coupled neurons can functionally play the role of XOR-gates. In addition, some studies try to show how these neurons can make logic gates using computational dynamical models of neurons.[18,19]For example, Boolean gate operations can be reproduced by integrated and firing models of neurons.[20]Furthermore,the logic gates implicated with neurons can be time variant,in other words,the logic gates can be dynamical.[21]

Thalamus neurons in cortico-thalamic circuits inhibit and excite cortex cells in different ways.[8]Both first-order and higher-order neurons of the thalamus excite the cortex pyramidal cells (PCs) of the fourth layer (l4).[22]These neurons excite vasoactive intestinal-peptide(VIP)cells,which indirectly inhibit PCs.[23]In addition, local basket cells (fast GABAer-gic), which induce inhibition to PCs, can be excited by thalamus nuclei.[24]Therefore, considering direct and indirect paths, thalamus nucleus can excite and inhibit cortical neurons. Cortex cells can interact with thalamic neurons by inhibiting and/or exciting them too. PCs in the cortex sixth layer(l6)can directly excite thalamus cells.[25]In addition,they can excite thalamic reticular nuclei(TRN),which inhibit thalamus cells.[26]

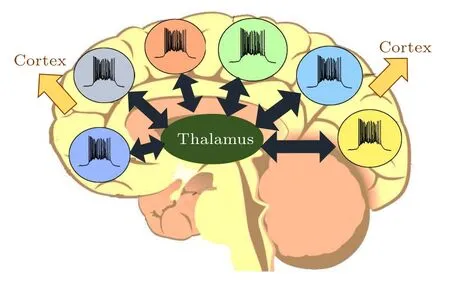
Fig.1. Vertical cortico-thalamic connectivity among different regions of the cortex and thalamus is shown with black bidirectional arrows.Different parts of the cortex can contact each other through the pathways that pass through the thalamus. Thalamus neurons can participate in the processing of information that passes through them.

Dynamical networks are capable of representing some collective behavior, such as synchronization.[27–31]In neuronal networks, studying the synchronization among different cortex parts with dynamical models leads to better comprehension of some diseases, such as epilepsies.[32]Considering the possible role of synchronized behavior of corticothalamic circuits in the treatment of epilepsies with deep brain stimulation[33]reveals the importance of models that try to explain how synchronization occurs. In addition,some cognitive tasks are associated with synchronization between parts of the cortex cells.[34]In special cases, while most of the neurons are synchronous, a few scatter from the total synchronized ones.[35]The few neurons that split off from the synchronized ones are named solitary ones and this behavior is called the solitary state.[35]The chimera state is another collective behavior among neurons that has been the center of attention of many researchers.[36–38]In a network of neurons,the chimera state refers to a state in which synchronization exists only in some groups of neurons,and others are asynchronous.[39]The chimera state has been observed in animals’uni-hemisphere sleep, local sleep in children’s brains, and also some psychological diseases, such as schizophrenia.[40]The chimera state has been investigated in multi-layer networks of computational dynamical neurons.[41]For instance,in a study,chimera was investigated in a network with two layers where the neurons of each layer were coupled electrically, while contacting through inhibitory and excitatory connections between the layers.[42]Controlling the chimera state in multilayer neuronal networks has also been investigated using pacemakers.[43]

This paper studies how thalamus neurons can affect the collective behavior of cortex neurons. To investigate the collective behavior of neurons,dynamical computational models,e.g. Hindmarsh–Rose or Izhikevich models, are used. These models can be considered as versions of Hodgkin—Huxley equations but are much simpler.[44]They can be coupled with each other to simulate chemical(excitatory and inhibitory)and electrical connections among neurons.[45]Here, Hindmarsh–Rose neurons are used to represent cortical cells. Thalamus neurons are logic gates that inhibit/excite the cortex layer’s neurons. Thus, a two-layer network is considered where its first and second layers represent cortex neurons and thalamus neurons, respectively. The connections are considered only among cortex and thalamus cells and cortical connections are ignored. Furthermore, both inhibitory and excitatory impacts of thalamus cells on cortex neurons are considered. Different factors such as types of logic gates (AND, OR, XOR)and their excitatory/inhibitory outputs are investigated. These simulations are done to assess how different functions of thalamus neurons can affect the collective behavior of the cortex. As mentioned, collective behavior among neurons has been reported in experimental observation. Therefore, studying them can be helpful,not only to comprehend how they are formed, but to use developed models for some applications,such as disease treatment. Thus, this paper’s simulations can be considered as a basic framework for studying the effects of cortico-thalamus connections on some cognitive functions and/or brain diseases, such as epilepsies, which are related to the neurons’ collective behavior. Consequently, here, the emergence of synchronization, chimera and solitary states is under consideration. The proposed two-layer network is explained in detail in Section 2. The results are presented in Section 3,and the conclusions are given in Section 4.

2. Model

A two-layer network is proposed with its first and second layers composed of Hindmarsh–Rose neurons as cortex cells and logic gates as thalamus nuclei,respectively(Fig.2).

The Hindmarsh–Rose equations for the first layer (the cortex layer)are described as follows:[46]

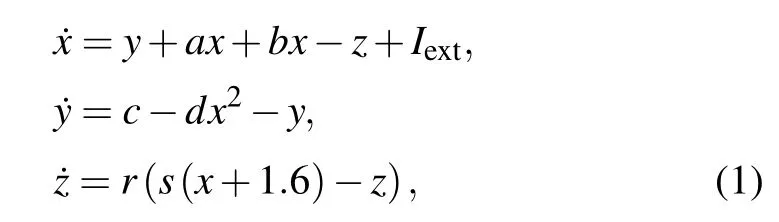
wherex,y, andzrepresent the membrane voltage, recovery current and adaption current,respectively. The other parameter values are set asa=1,b=2.5,c=1,d=5,r=0.006,s=4,andIext=2.2. In the cortex layer,N=100 Hindmarsh–Rose neurons are considered.

For the second layer(thalamus layer),logic gates(AND,OR and XOR) are considered. The number of each type ofgate in the thalamus layer is represented by ANDNUM, ORNUM,and XORNUM variables,respectively. The outputs of each of these gates can be inhibitory or excitatory. Each of the logic gates takes its inputs from two random Hindmarsh–Rose neurons of the first layer. The logic gates give their outputs randomly to some Hindmarsh–Rose neurons. The output number of each gate(AND,OR and XOR)is represented by ANDOUT,OROUT,and XOROUT variables,respectively.The type of outputs of logic gates are shown with a TYPE variable,which can be excitatory(E)or inhibitory(I)(TYPE=E,orI).

Consideringxiandxjas the voltages of two Hindmarsh–Rose neurons that are a logic gate’s inputs,the gate’s outputs can excite/inhibit (k)th Hindmarsh–Rose neurons according to the following equations:

whereand max(xi,xj)are designed to always choose the voltage (x) that is in the burst state(and not the one that is in the rest state).θs=−0.75,λ=100,Vse=2,andVsi=−1.5 are set as the parameters of the interaction among neurons.geandgiare considered as coefficients of excitatory and inhibitory connections, respectively. The gates can be OR,AND,and XOR.Thus, the gate conditions are as follows:

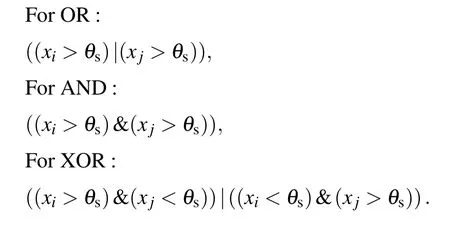
According to Eq.(2),the connections of two layers of the network are defined. Each logic gate gets its inputs from two Hindmarsh–Rose neurons and gives excitatory/inhibitory outputs to a number of the cortex layer neurons according to Eq.(2). These connections are determined randomly.

As a feature of coherency, the strength of incoherence(SI)[47]is calculated for different states of the network. Consideringwl,i=xl,i −xl,i+1, i=1,2,...,N, l=1,2,...,d,andn=N/M,calculation ofSIcan be done as follows:[47]

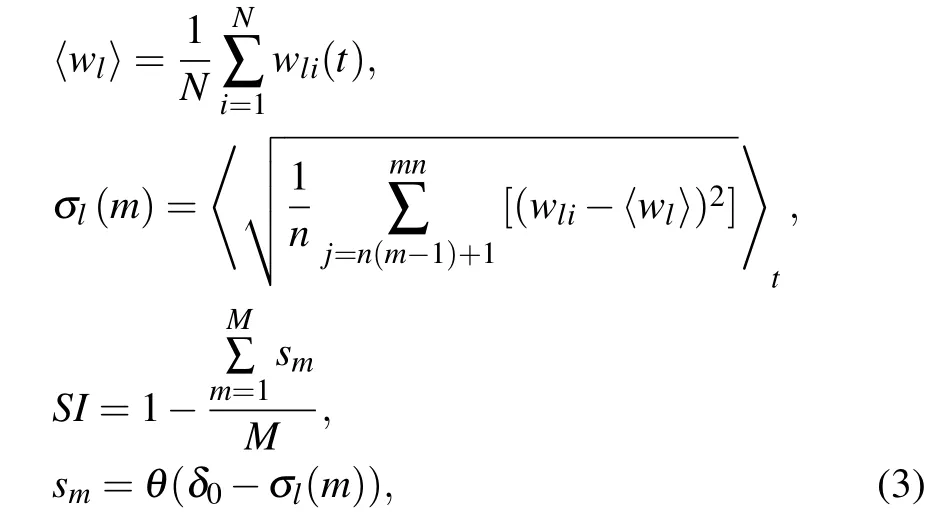
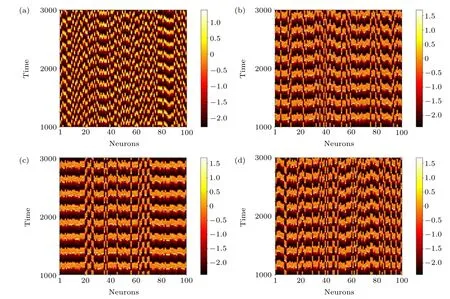
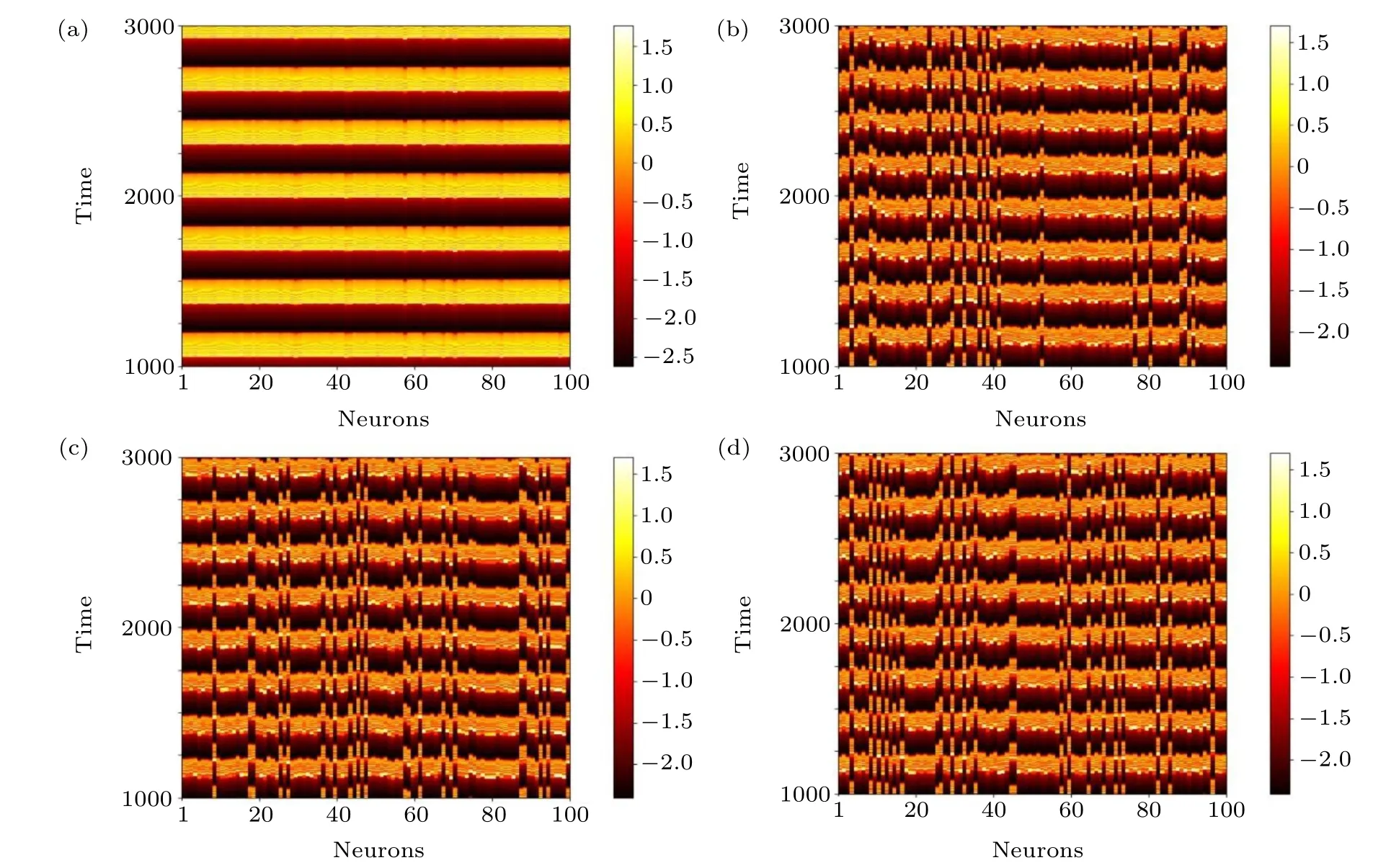
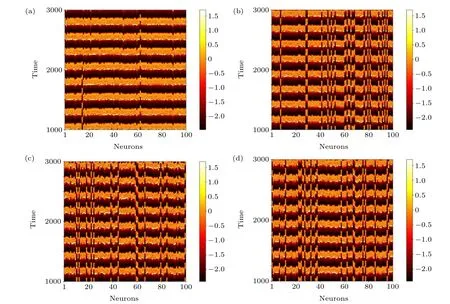
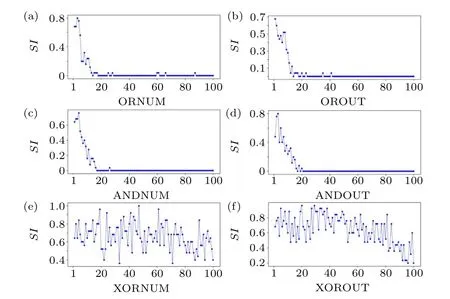
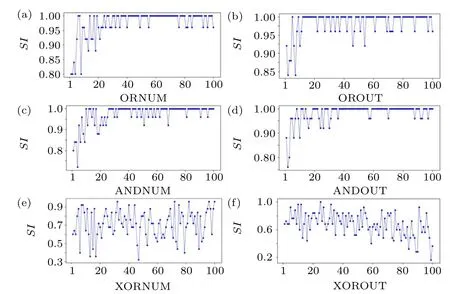
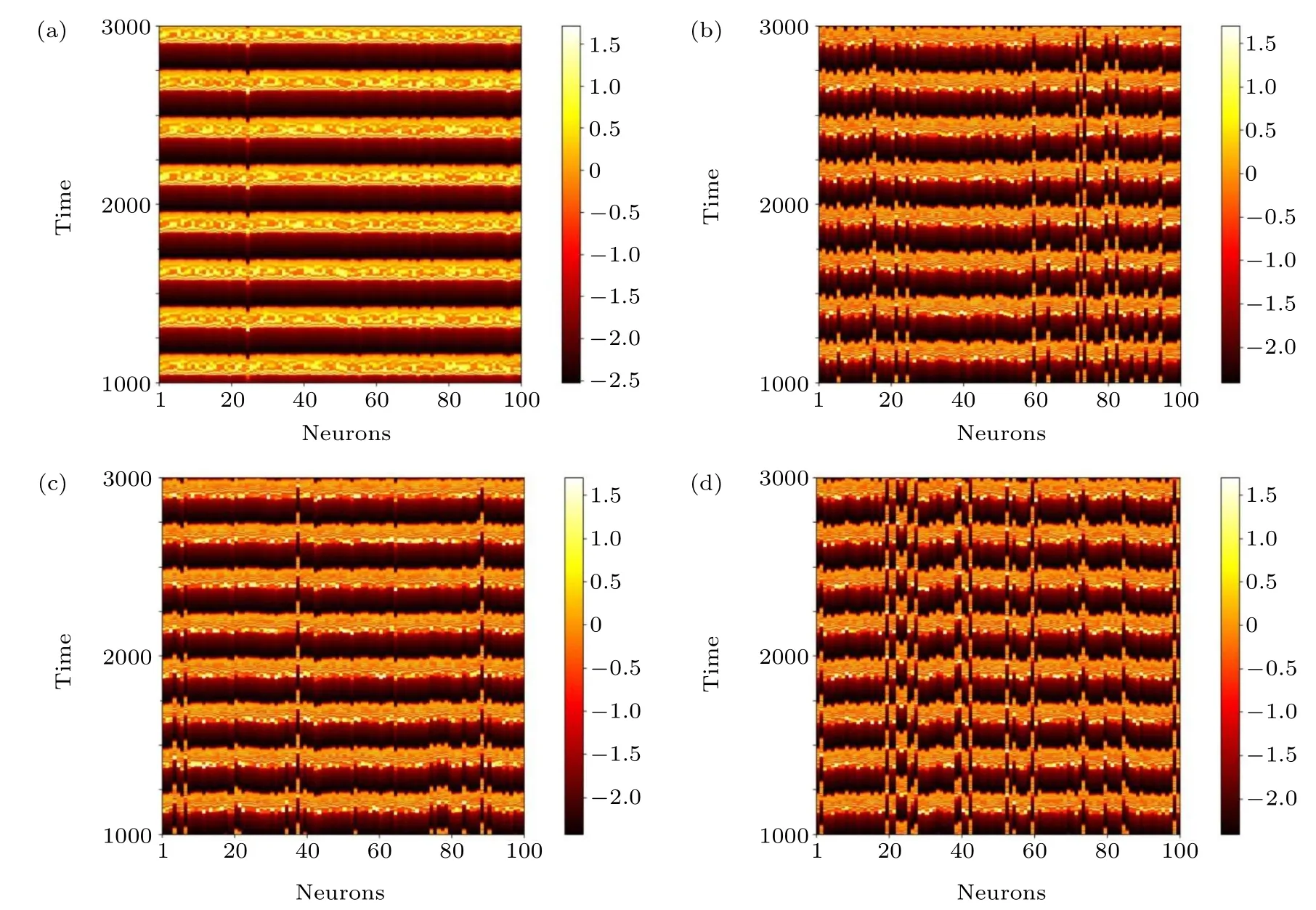
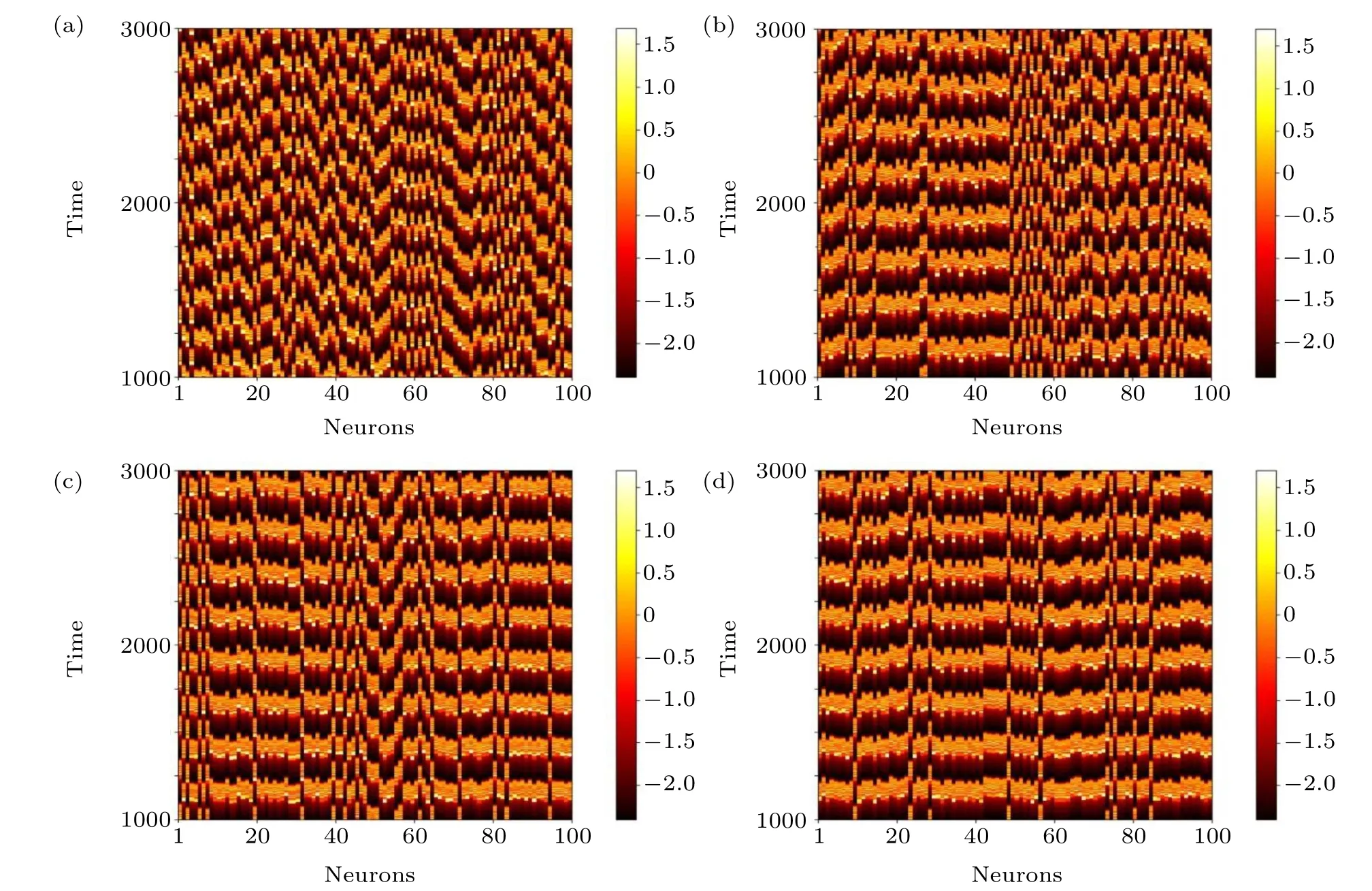
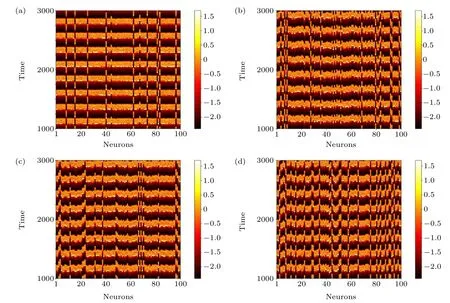
where〈···〉tis the average over time,θ(·) is the Heaviside function andδ0is a predefined threshold.SI=0,SI=1,and 0

Fig.2. Schematic of the introduced cortex-thalamus network: the top layer(cortex layer)is constructed with Hindmarsh–Rose neurons and the thalamus layer has logic gates. Each logic gate gets its inputs from two Hindmarsh–Rose neurons that are determined randomly. Outputs of each logic gate can be either excitatory or inhibitory.

3. Results and discussion

To solve the equations of the network, the Runge–Kutta method (4th order) is used. To investigate logic gates’effects(AND,OR,XOR)on the collective behavior of neurons in the cortex layer, different situations are considered. In each situation, just one type of logic gate exists in the thalamus layer and the gates’outputs are just inhibitory or excitatory. The figures related to the inhibitory types of logic gates are demonstrated in the appendix section to avoid repeating spatiotemporal plots.

First,it is considered that only OR-gates exist in the thalamus layer and the outputs of all gates are inhibitory(Fig.3).Spatiotemporal patterns of neurons of the cortex layer can be seen in Fig. 3. Different numbers of OR-gates are assumed.Input neurons of each OR-gate and its outputs are determined randomly. When a large number of inhibitory OR-gates with a large number of outputs for each gate are considered, the network state is asynchronous(Fig.3(a)). In Figs.3(b)–3(d),the number of inhibitory OR-gate outputs,inhibitory OR-gate number, and both these variables are decreased, respectively.Considering a large number of inhibitory OR-gates with a few outputs causes the decline of asynchronization among neurons(Fig. 3(b)). On the other hand, a small number of inhibitory OR-gates,when each has many outputs,changes the networkstate to the chimera state (Fig. 4(c)). Figure 3(d) shows that lower values for both OR-gate numbers and output numbers rather than the situation of Fig.3(a),decrease the incoherency of the network.

Fig. 3. Thalamus layer contains only OR-gates with inhibitory outputs (TYPE=I, gi =0.01). Spatiotemporal diagrams of neuron activity are shown. (a)ORNUM=100,OROUT=90,(SI=1). (b)Outputs of the gates are decreased rather than situation(a)(ORNUM=100,OROUT=1)and the coherency of the network slightly increases (SI =0.96). (c) Number of gates are decreased rather than situation (a) (ORNUM=3,OROUT=90)and the network state changes to chimera(SI=0.72). (d)Both gate outputs and gate numbers are decreased rather than situation(a)(ORNUM=10,OROUT=10)and the network coherency is slightly increased(SI=0.96).

Fig. 4. Thalamus layer contains only AND-gates with excitatory outputs (TYPE=E, ge =0.01). Spatiotemporal diagrams of neuron activity are shown. (a)ANDNUM=100,ANDOUT=70: the network is synchronous(SI=0). (b)ANDNUM=100,ANDOUT=1,(SI=0.72). (c)ANDNUM=3, ANDOUT=70, (SI=0.72). (d)ANDNUM=10, ANDOUT=10, (SI=0.76). Decreasing the number of gates or outputs or both,results in more incoherency and leads to the chimera state.

Fig.5. Thalamus layer contains only XOR-gates with excitatory outputs(TYPE=E,ge=0.01). Spatiotemporal diagrams of neuron activity are shown. (a)XORNUM=100 and XOROUT=80: the cortex layer state is chimera(SI=0.36)(b)XORNUM=3,XOROUT=80,(SI=0.67).(c)XORNUM=100,XOROUT=5,(SI=0.80). (d)XORNUM=10,XOROUT=10,(SI=0.72). Lower values for both variables rather than the situation in part(a)leads to an increase in incoherency in the network. However,the network is still in the chimera state.

Fig.6. Both XOR gates(TYPE=I, XORNUM=3, XOROUT=10, gi =0.9)and AND gates(TYPE=E, ANDNUM=10, ANDOUT=40,ge =0.01)are considered. (a)Spatiotemporal diagram of the neuron activity is plotted. State of the network is the solitary state(SI=0.08). (b)Temporal pattern of the solitary neurons. (c)Temporal pattern of the synchronous neurons.

In the next step, the excitatory OR-gates are assumed in the thalamus layer (Fig. A1 in the appendix). Spatiotemporal patterns of the cortex layer neurons with different numbers of OR-gates and outputs are shown in Fig. A1. When a large number of excitatory OR-gates with many outputs are considered, the state of the neurons in the cortex layer is imperfect synchronization (Fig. A1(a)). Considering a lower number for the excitatory OR-gates’ results in the chimera state (Fig. A1(b)). A lower number of outputs for the excitatory OR-gates, when the OR-gates’outputs are the same as Fig. A1(a), also causes the chimera state (Fig. A1(c)). Figure A1(d) demonstrates the situation in which both numbers of gates and their outputs decrease, which similarly leads to the chimera state.

After investigating the OR-gate,the AND-gate is considered. The cortex layer’s spatiotemporal patterns are plotted in Fig.4.For a large number of excitatory AND-gates when each gate has many outputs, the network becomes zero-lag synchronous(Fig.4(a)). Decreasing the number of outputs rather than the past situation causes the chimera state to be revealed(Fig. 4(b)). Decreasing the number of excitatory AND-gates(rather than the situation of(Fig.4(a)))results in the chimera state(Fig.4(c)).Decreasing the value of both variables(ANDgate number and outputs)causes the network state to becomethe chimera state too(Fig.4(d)).

Next, the inhibitory AND-gates are assumed in the thalamus layer. Spatiotemporal patterns of the Hindmarsh–Rose layer are demonstrated in Fig. A2. When a large number of inhibitory AND-gates with a large number of outputs for each gate is assumed, the state of neurons in the Hindmarsh–Rose layer is asynchronization(Fig.A2(a)).A lower number for the outputs decreases the level of asynchronization (Fig. A2(b)).A low number of inhibitory AND-gates rather than the situation of Fig. A2(a) similarly reduces the asynchrony level of the Hindmarsh–Rose neurons (Fig. A2(c)). Finally, considering lower values for both AND-gate number and outputs(rather than the Fig. A2(a) situation) results in the chimera state(Fig.A2(d)).

The final logic gate to investigate is XOR.First,the gates are considered to be excitatory. The cortex layer’s spatiotemporal patterns for the excitatory XOR are shown in Fig. 5.For a large number of excitatory XOR-gates, with many outputs, the network is in the chimera state with high coherency(Fig. 5(a)). Reducing the number of excitatory XOR-gates rather than in the Fig. 5(a) situation, decreases the level of coherency, although the behavior is still the chimera state(Fig. 5(b)). Decreasing the number of outputs also results in a lower level of coherency (Fig. 5(c)). Figure 5(d) illustrates that there is a similar effect when both variables are decreased.

Finally, the inhibitory XOR-gates are considered. The Hindmarsh–Rose layer’s spatiotemporal patterns are shown in Fig. A3. For a larger number of inhibitory XOR-gates with many outputs, the network state is the solitary state(Fig.A3(a)). Decreasing the number of outputs increases the incoherency of the network and leads to the chimera state(Fig.A3(b)). Figure A3(c)shows that reducing the number of inhibitory XOR-gates rather than the situation of Fig.A3(a)results in the chimera state too.Finally,by decreasing the values of both variables (XOR-gate numbers and their output numbers), the network’s state remains chimera with more asynchronous neurons(Fig.A3(d)).

After investigating how different types of logic gates separately affect the collective behavior of the Hindmarsh–Rose layer,a combination of different logic gates is considered. For this situation,some inhibitory XOR-gates and some excitatory AND-gates are considered. The resultant spatiotemporal pattern of this network can be observed in Fig.6(a). The neurons under these conditions create a solitary state. A few solitary neurons have the temporal pattern of Fig.6(b),while the time series of most of the neurons is as shown in Fig.6(c).

The network is examined more thoroughly by computing the strength of incoherence through considering only one logic gate. The results for excitatory gates are shown in Fig.7.In Figs. 7(a), 7(c), and 7(e), the number of gates is varied and a median value for the gates’ outputs is considered. In Figs.7(b), 7(d), and 7(f)the number of gates is fixed and the number of gates’outputs is varied. It is observed that increasing the number of OR-gates and AND-gates makes the network more synchronous. The same pattern can be seen when the outputs of the OR-gates and AND-gates are increased. On the other hand, changing the number of XOR-gates or their outputs does not change the behavior of the network and the network remains in the chimera state.

Fig.7.The SI values when the outputs of the thalamus layer are all excitatory(TYPE=E,ge=0.01).(a)SI versus the OR-gate number for OROUT=50.(b)SI versus the OR-gate outputs for ORNUM=50. (c)SI versus the ANDgate number for ANDOUT=50. (d)SI versus the AND-gate output number for ANDNUM=50.(e)SI versus the XOR-gate number for XOROUT=50.(f) SI versus the XOR-gate output number for XORNUM=50. Increasing the OR-gates and AND-gates or their outputs increases the network’s coherency,while for different XOR-gate numbers or outputs the chimera state remains.

Fig.8. The SI values when all thalamus layer’s gates are inhibitory(TYPE=I, gi = 0.01). (a) SI versus the OR-gate number for OROUT = 50. (b)SI versus the OR-gate outputs for ORNUM=50. (c) SI versus the ANDgate number for ANDOUT=50. (d)SI versus the AND output number for ANDNUM=50. (e) SI versus the XOR-gate number for XOROUT=50.(f) SI versus the XOR-gate output number for XORNUM=50. Increasing the OR-gates and AND-gates or their outputs decreases the network’s coherency. With changing the parameters of the XOR-gate numbers or outputs,the chimera state is preserved.

The values of the strength of incoherence for inhibitory gates are shown in Fig. 8. In Figs. 8(a), 8(c), and 8(e), a median value for the number of outputs is considered and the number of gates is changed, and in Figs. 8(b), 8(d), and 8(f),the number of gates is fixed and the gates’outputs are varied.It can be observed that increasing the gate number or gate output for OR-gates and AND-gates results in more asynchrony in the network. While for XOR-gates, the network’s behav-ior is the same as the excitatory case and the chimera state is preserved by changing the parameters.

4. Conclusion

In this paper, a two-layer network was introduced as a framework for studying cortico-thalamic circuits. In fact, the effect of the thalamus on the collective behavior of cortical neurons was investigated. This framework can be used for further investigation of the roles that thalamus neurons can play in the collective behavior of the cortex. Cortico-thalamus connections are paths from which different cortex regions can interact with each other.Therefore,investigating their relation to the cortex’s neuron synchronization can be helpful in finding treatment for some diseases, such as epilepsies. In addition,these frameworks can help one to comprehend how the cognitive functions that are correlated with some observed collective behavior are performed. In the designed two-layer network,the first layer was built with Hindmarsh–Rose models to represent the cortical cells,while the second layer was built with logical gates. However, the relationship between the brain’s cortex and thalamus neurons is much more complex than the introduced network.However,this framework has the capability of revealing some aspects of the cortico-thalamic circuits and needs further expansion in future research. In this work,the direct relationship between the cortex regions and also the effect of the other parts of the brain on the cortico-thalamic circuits were ignored. It was shown that the inhibitory OR-gates lead the network towards asynchronization, while the excitatory OR gates increase synchronization. In addition,it was revealed that the high number of excitatory and inhibitory AND gates makes the network synchronous and asynchronous, respectively,while a few of these gates create the chimera state.Furthermore, both inhibitory and excitatory XOR gates can result in the chimera solution for the network. In addition,it was demonstrated that considering a combination of excitatory AND-gates and inhibitory XOR-gates causes the network’s state to become the solitary state. However, different combinations of logic gates can be considered, which is suggested for future studies. Furthermore, since the discrete and continuous models of neurons exhibit different behavior, we suggest that the effect of different logic gate types on populations of discrete models of neurons be investigated in future research.

Acknowledgment

One of the authors Sajjad Shaukat Jamal extends his gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through the research groups program(Grant No.R.G.P.2/48/42).

Appendix A

Fig.A1. Thalamus layer contains only OR-gates with excitatory outputs(TYPE=E,ge=0.01). Spatiotemporal diagrams of neuron activity are shown. (a)ORNUM=100,OROUT=30:. Network state is imperfect synchronization(SI=0.04). (b)ORNUM=5,OROUT=30,(SI=0.56).(c)ORNUM=100,OROUT=3,(SI=0.48). (d)ORNUM=10,OROUT=10,(SI=0.64). Lower number for OR-gates or OR-outputs or both these variables increase the incoherency and lead to the chimera state.

Fig.A2. Thalamus layer contains only AND-gates with inhibitory outputs(TYPE=I,gi=0.01). Spatiotemporal diagrams of neuron activity are shown.(a)ANDNUM=100 and ANDOUT=70.Cortex layer’s state is asynchronous(SI=1).(b)ANDNUM=100,ANDOUT=2,(SI=0.96).(c)ANDNUM=3,ANDOUT=70,(SI=0.92). (d)ANDNUM=10,ANDOUT=10,(SI=0.80). Decreasing the outputs of the AND-gates or the number of AND-gates or both these variables results in a slight increment in the coherency level of the network.

Fig.A3. Thalamus layer contains only XOR-gates with inhibitory outputs(TYPE=I,gi=0.01). Spatiotemporal diagrams of neuron activity are shown. (a)XORNUM=100, XOROUT=70. Behavior is the solitary state(SI=0.48). (b)XORNUM=100, XOROUT=5, (SI=0.72). (c)XORNUM=3,XOROUT=70,(SI=0.52). (d)XORNUM=10,XOROUT=10,(SI=0.84). Setting a lower value for gate number or output number or both variables rather than part(a),makes the network more incoherent and changes the network’s state to the chimera.