Quantum transport signatures of non-trivial topological edge states in a ring-shaped Su-Schrieffer-Heeger double-chain system
Cheng-Zhi Ye(叶成芝) Lan-Yun Zhang(张蓝云) and Hai-Bin Xue(薛海斌)
1School of Physics and Electronic Engineering,Linyi University,Linyi 276005,China2Key Laboratory of Interface Science and Engineering in Advanced Materials,Ministry of Education,Taiyuan University of Technology,Taiyuan 030024,China
In the ring-shaped Su–Schrieffer–Heeger (SSH) double-chain, the quantum interference between the two different electron tunneling paths of the upper and lower chains has an important influence on the electron transport properties of non-trivial topological edge states. Here,we have studied the electron transport signatures of non-trivial topological edge states in a ring-shaped SSH double-chain system based on the wave-guide theory and transfer-matrix method. In the ringshaped SSH double-chain with the upper chain being different from the lower one, it is demonstrated that the electron transmission probability displays the four and two resonance peaks associated with the non-trivial topological edge states in the weak and strong coupling regimes,respectively. Whereas in the case of the upper chain being the same as the lower one, the two transmission resonance peaks associated with the non-trivial topological edge states in the weak coupling regime are only found, and that in the strong coupling regime disappear that originated from the destructive interference between the two different electron tunneling paths of the upper and lower chains. Consequently,the variation of the number of transmission resonance peaks associated with the non-trivial topological edge states in the weak and strong coupling regimes suggests that an alternative scheme for detecting non-trivial topological edge states in the ring-shaped SSH doublechain system.
Keywords: ring-shaped Su–Schrieffer–Heeger double-chain,non-trivial topological edge states,transmission probability
1. Introduction
Non-trivial topological edge states have potential applications in spintronics and quantum computation because they have a strong robustness against local material defects and disorders.[1,2]The one-dimensional Su–Schrieffer–Heeger(SSH) chain,[3]which was originally used to describe polyacetylene molecule, is one of the simplest systems with non-trivial topological edge states. Particularly, the SSH models have been experimentally realised with the photonic lattices,[4–6]optical lattices,[7]engineered atomic chains[8,9]and microring array.[10]To realize quantum devices based on non-trivial topological edge states, how to detect the edge states is one of the important topics. Consequently, how to determine the existence of non-trivial topological edge states in the SSH chain systems has become an important topic in condensed matter physics.[11–23]Recently,it has been demonstrated that electron transport properties associated with nontrivial topological edge states can be used to determine the existence of the non-trivial topological edge states.[24–30]Compared with the SSH chains being of the topologically trivial and plain phases, the (Andreev) conductance and the shot noise of the topologically nontrivial chain in the zero-bias limit display an opposite odd–even parity effects.[26]In particular,the transport current and its Fano factor can be used to distinguish whether the SSH chain system is of the topologically non-trivial or trivial phases.[27,28]For example,in the vicinity of the zero energy,the variation of the number of transmission resonance peaks in the weak and strong coupling regimes can be used to detect whether the SSH chain is of the nontrivial topological state or not and determine the winding numbers of different nontrivial topological states.[29,30]Interestingly,in a ring-shaped SSH double-chain system,which is contrary to the two coupled SSH double chains,[16,17,30]the conduction electrons from the source electrode have two different paths through the SSH system and tunnel into the drain electrode. In this case,the two different electron tunneling paths can exhibit the quantum interference effect. However,the influence of the quantum interference between the two different electron tunneling paths on the electron transport properties of non-trivial topological edge states in a ring-shaped SSH double-chain system has not yet been revealed.[31–36]
In this paper, we study the electron transport signatures of non-trivial topological edge states in a ring-shaped SSH double-chain system,and discuss the dependence of the electron transport properties of edge states on the quantum interference between the two different electron tunneling paths of the upper and lower chains. In the case of the upper chain being different from the lower one, the four and two trans-mission resonance peaks associated with the non-trivial topological edge states in the weak and strong coupling regimes can be found, respectively. Whereas in the case of the upper chain being the same as the lower one,the number of the transmission resonance peaks in the weak coupling regime is only two, and the two transmission resonance peaks in the strong coupling regime will disappear that originating from the destructive interference between the two different electron tunneling paths of the upper and lower chains. Importantly, the number of the corresponding transmission resonance peaks in the strong coupling regime is also reduced by two. Therefore,with increasing the strength of tunneling coupling between the ring-shaped SSH double-chain and the two external electrodes from the weak to the strong coupling regimes, the non-trivial topological edge states can be detected by observing the variation of the number of transmission resonance peaks associated with the non-trivial topological edge states in the vicinity of the zero energy.
The paper is organized as follows. In Section 2, we introduce the ring-shaped SSH double-chain system, and outline the procedure to calculate the transmission probability of electron transport through the ring-shaped SSH double-chain system based on the wave-guide theory and transfer-matrix method. The numerical results are discussed in Section 3,where we first discuss the topological properties of the nontrivial edge states of the SSH single-chain,and then study the influence of the quantum interference between the two different electron tunneling paths of the upper and lower chains on the electron transport properties of non-trivial topological edge states in the ring-shaped SSH double-chain system, and suggest an alternative scheme for detecting its non-trivial topological edge states. Finally, in Section 4 we summarize the work.
2. Model and formalism
2.1. The ring-shaped SSH double-chain system
The ring-shaped SSH double-chain, which consists of the two SSH chains connected in parallel to two leads, see Fig.1(a),is described by the Hamiltonian
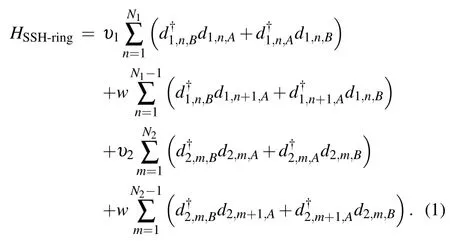
The first and second terms describe the upper SSH chain,and the third and fourth terms describe the lower SSH chain.Here,is the creation(annihilation)operator of an electron atβ(β=A,B)sublattice inn-th cell of the upper chain of the ring-shaped SSH double-chain,υ1the intra-cell hopping amplitude of the upper chain andwinter-cell hopping one of the upper and lower chains; while in the case of the lower chaini=2.N1andN2are the number of cells of the upper and lower chains,respectively.
The two leads are modeled as the Hamiltonian
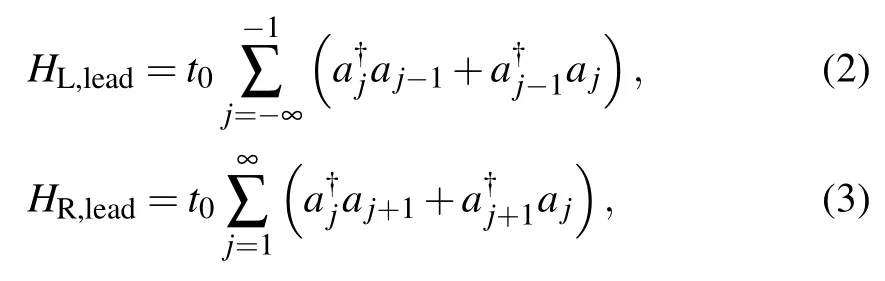
whereis the creation(annihilation)operator of an electron atj-th lattice in the leads, andt0the hopping amplitude between two nearest-neighbor lattices in the leads. The electron tunneling between the ring-shaped SSH double-chain and the two leads reads

wheretα,1(tα,2)is the amplitude of electron tunneling between theα-lead and the upper(lower)chain of the ring-shaped SSH double-chain.
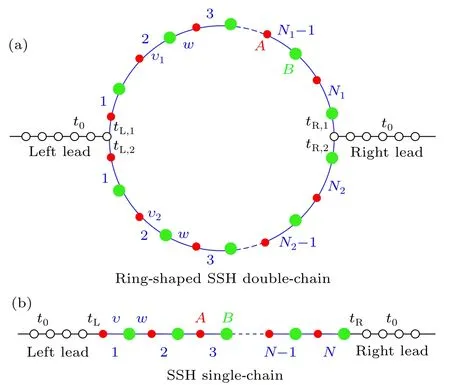
Fig.1. Schematics of the considered ring-shaped SSH double-chain and the SSH single-chain systems coupled to the left(source)and right(drain)leads(electrodes). The hollow circles denote lattices on the leads, and red and green circles describe the sublattices A and B of the SSH chain,respectively.t0 describes the hopping amplitude between the two nearest-neighbor lattices on the leads. (a)tα,1 (tα,2) characterizes the strength of tunneling coupling between the upper(lower)chain and the α-electrode, and υ1 (υ2)the intracell hopping amplitude of the upper(lower)chain, and w inter-cell hopping amplitude of the upper and lower chains.N1 and N2 are the number of cells of the upper and lower chains,respectively. (b)υ and w describe the intra-cell hopping amplitude and the inter-cell hopping amplitude of the SSH singlechain, respectively. tα characterizes the strength of tunneling coupling between the SSH single-chain and the α-electrode, N denotes the number of cells of the SSH single-chain.
2.2. The transmission probability and transfer-matrix method
To calculate transmission probability of electron transport through the ring-shaped SSH double-chain, the wave-guide theory and transfer-matrix method are adopted in the following calculation. In the Wannier basis,the wave function of the total system|Ψ〉can be expressed as
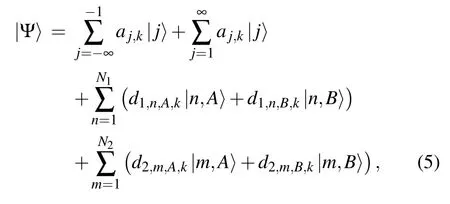
where the coefficientsaj,kandd1,n,β,k(d2,n,β,k)correspond to the probability amplitudes atj-th lattice in the leads andβsublattice inn-th cell of the upper (lower) chain of the ringshaped SSH double-chain,respectively. Inserting Eq.(5)into the time-independent Schrödinger EquationH|Ψ〉=E|Ψ〉,by setting the coefficients of Wannier states on the left-hand side of the equation being equal to that on the right-hand side,the following set of coupled linear equations can be obtained as
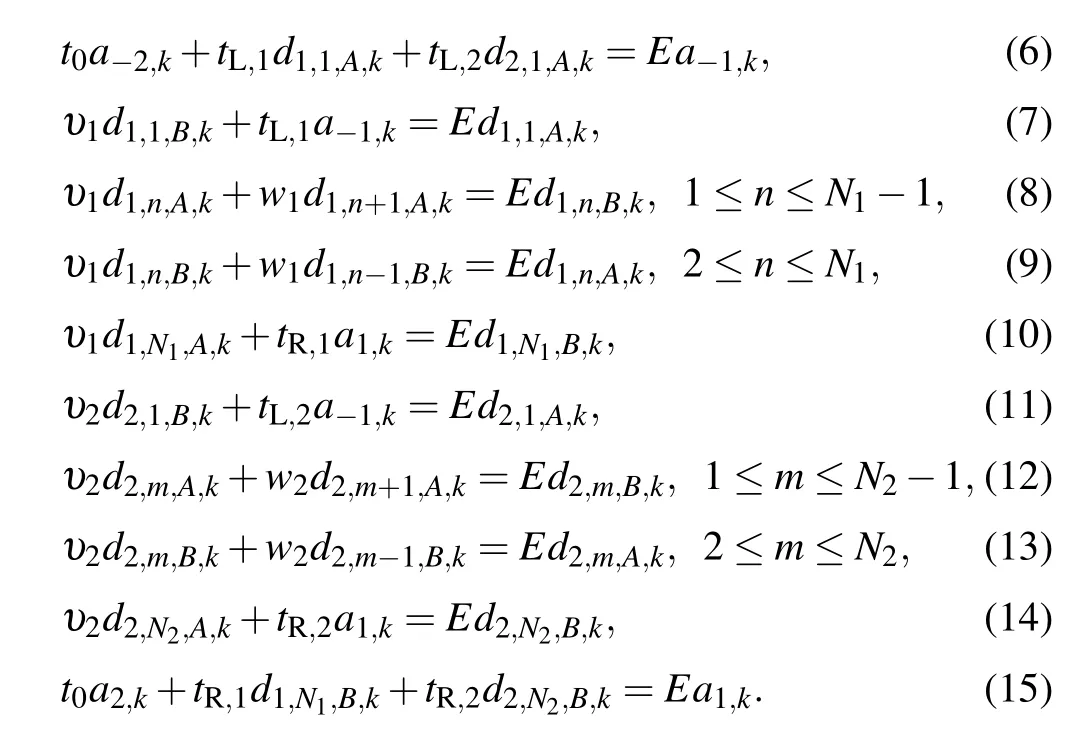
Using transfer-matrix method, Eqs. (8)–(14) can be reexpressed as
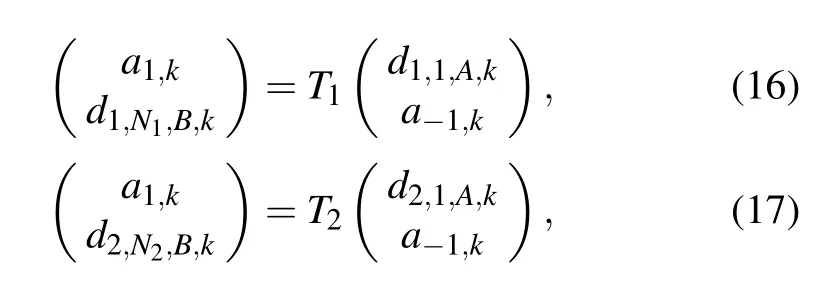
with
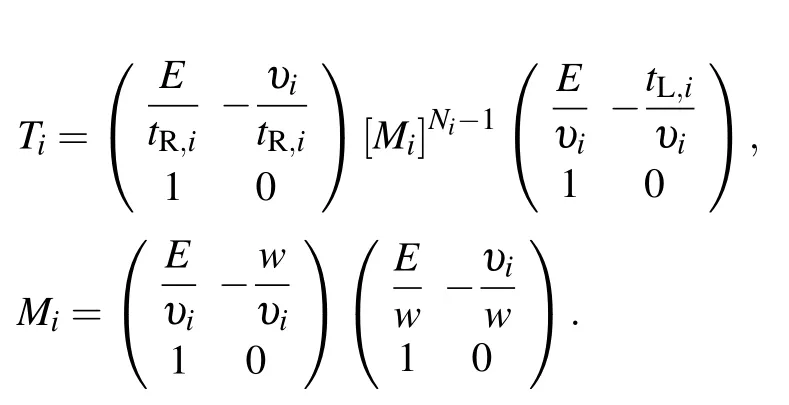
Moreover,Eqs.(16)and(17)can be further written as
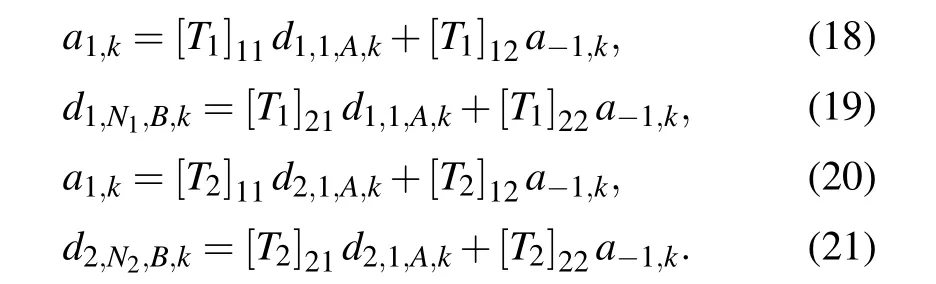
To simplify the calculation,the wave functions associated with the conduction electrons are chosen as plane waves, and the corresponding wave amplitudes of the left and right leads read as

Then,inserting Eqs.(22)and(23)into Eqs.(6),(18)–(21),and(15),the six coupled linear equations can be rewritten as

By solving the above coupled linear equations, the transmission probability of electron through the ring-shaped SSH double-chain system is given by

3. Results and discussion
We now study the transmission probabilities of electron transport through the ring-shaped SSH double-chain system in the vicinity of the zero energy. In the following numerical calculations, the parameters of the ring-shaped SSH doublechain system are chosen astL,1=tL,2=tL,tR,1=tR,2=tR,tL=tR=t,t0=1.0,andw=1.0.To investigate electron transport signatures of the non-trivial edge states in the ring-shaped SSH double-chain,we first discuss the SSH single-chain system.
3.1. The topological properties of the SSH single-chain
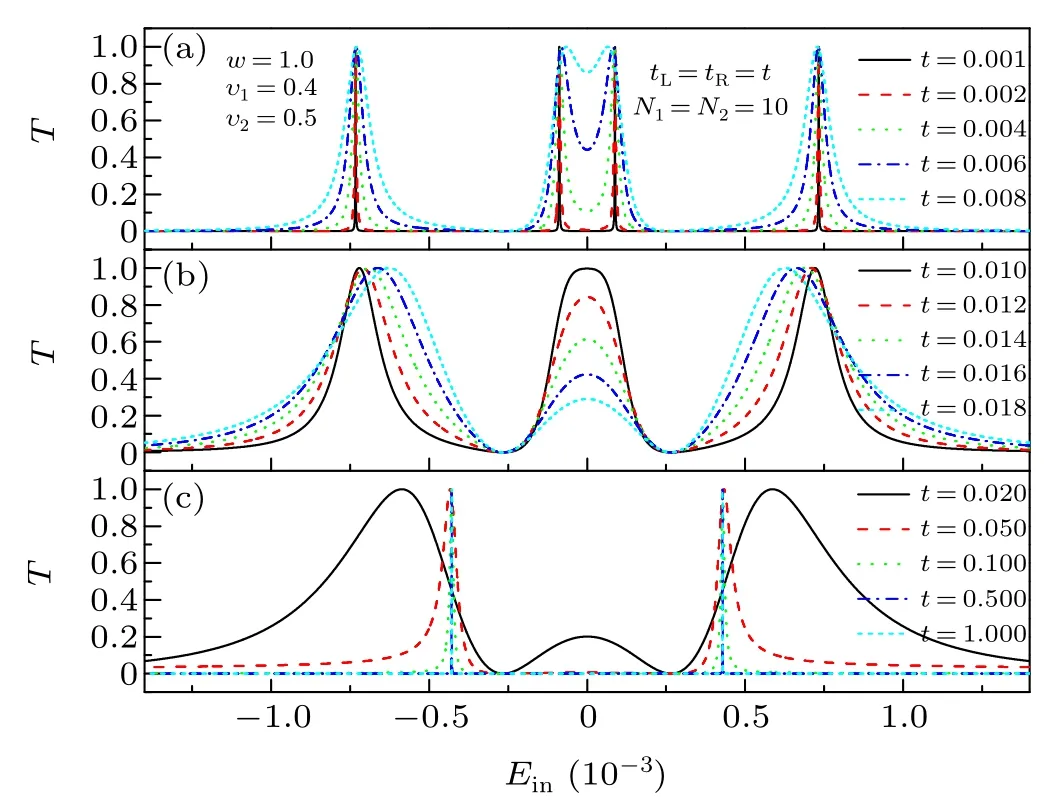
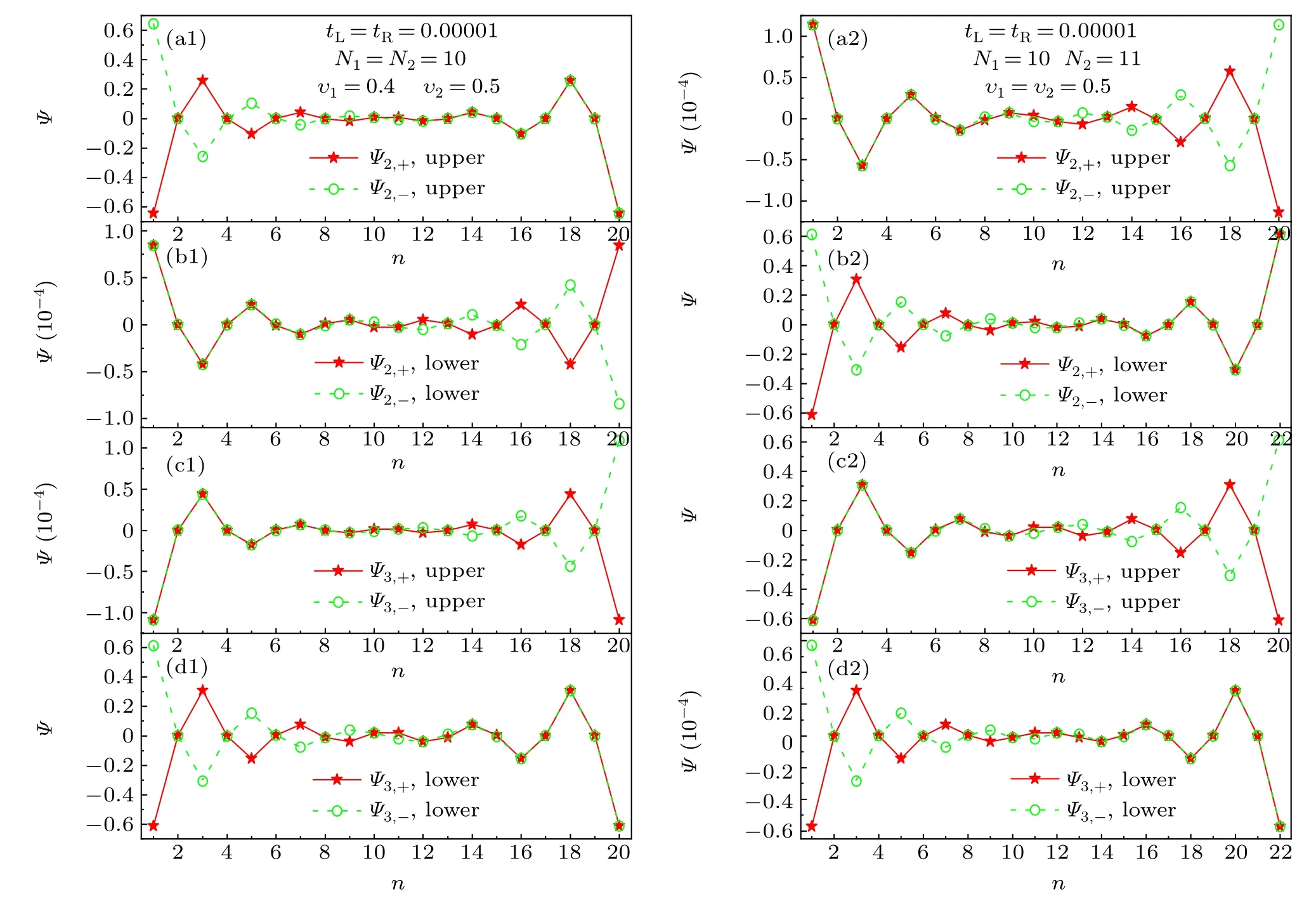
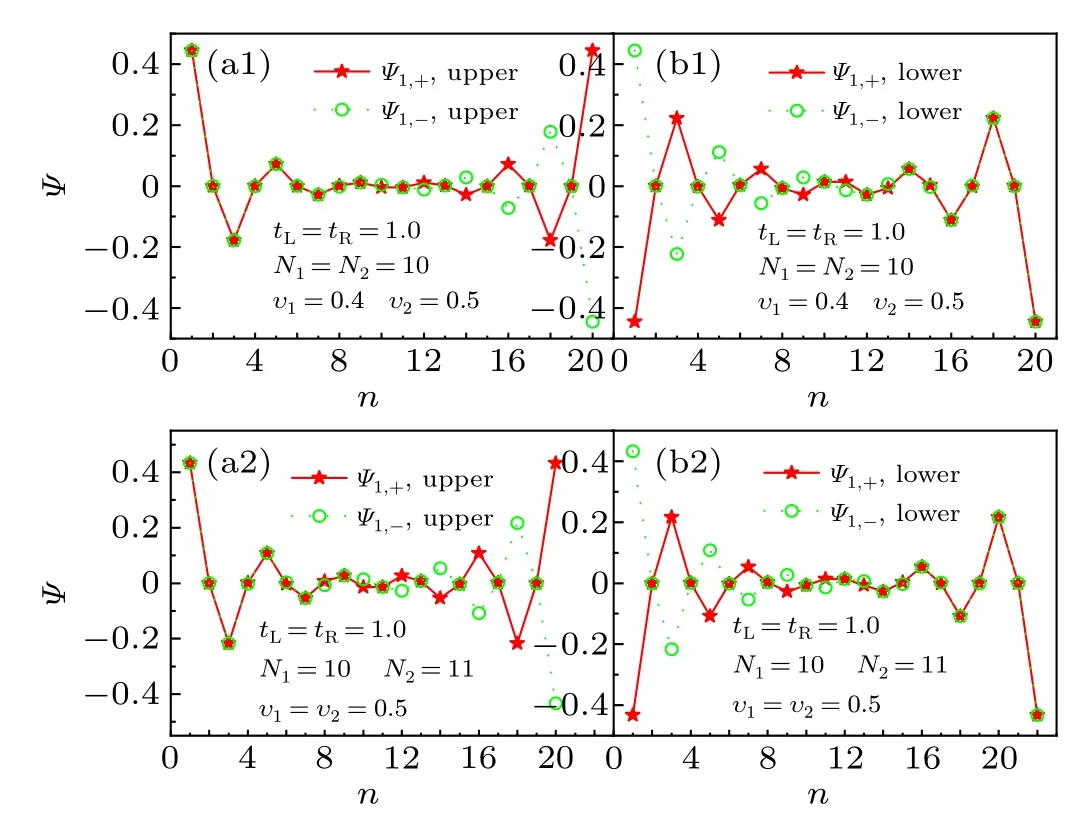
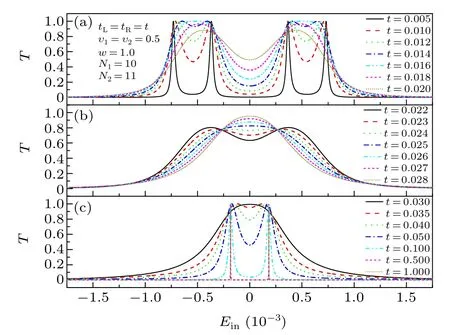
In a finite-length SSH single-chain,the energy difference between the two non-trivial topological edge states is not equal to zero,which depends on the intra-cell hopping amplitudeυ,see Fig.2(a). Moreover,for a given intra-cell hopping amplitudeυ,the energy difference between the two non-trivial topological edge states depends on the length of SSH single-chain,namely, the number of cellsN, see Fig.2(b). To characterize the non-trivial topological properties of the SSH single-chain,we here choose the winding number to describe the non-trivial topological edge states. For a infinite SSH single-chain, the winding number of non-trivial topological edge states is equal to 1 whenυ Fig. 2. (a) The energy spectrum of the finite-length SSH single-chain with N =10. (b) The energy spectrum of the non-trivial topological edge states for different finite-length SSH single-chain. (c) and (d) The transmission probabilities of electron transport through the SSH single-chain in the vicinity of the zero energy as a function of the energy of incident electron. (c)The same finite-length SSH single-chain for different intra-cell hopping amplitudes with N =10 and tL =tR =0.0005. (d) The different finite-length SSH single-chain with υ =0.5 and tL =tR =0.001. The inter-cell hopping amplitude of the SSH single-chain is chosen as w=1.0. To explore the dependence of the non-trivial topological edge states of the SSH single-chain on the electron transport properties, we study the electron transport through the finite-length SSH single-chain in the vicinity of the zero energy.When the SSH single-chain weakly coupled to the source and drain leads,the positions of transmission resonance peaks in the vicinity of the zero energy can characterize the energy spectrum of the non-trivial topological edge states, see Figs. 2(c) and 2(d). Consequently, the properties of transmission resonance peaks associated with the non-trivial topological edge states suggest an alternative scheme to determine whether the SSH single-chain is of the non-trivial topological edge states or not. In general,to detect the non-trivial topological edge states of the SSH single-chain based on the properties of transmission resonance peaks in the vicinity of the zero energy, it is necessary to study the signatures of transmission resonance peaks associated with the non-trivial topological edge states as a function of the externally tunable physical quantities. Here,we select the strength of tunneling coupling between the SSH single-chain and the two leadstL=tRas a tunable physical quantity. In the case of the SSH single-chain weakly coupled to the source and drain leads, e.g.,tL=tR=0.004, the transmission probability of the SSH single-chain in the vicinity of the zero energy displays the two resonance peaks,see the solid line in Fig.3(a). With increasing the tunneling coupling strengthtL=tR, the two transmission resonance peaks first evolved into a relatively wide resonance peak gradually, and then the wide resonance peak disappears finally when the tunneling coupling strengthtL=tRreaches a certain value, e.g.,tL=tR=0.05, see Fig. 3(a). We next illustrate the physical mechanism of electron transport properties of the SSH singlechain in the vicinity of the zero energy. In the case of the SSH single-chain coupled to the two leads,the energy spectrum of the SSH single-chain will be influenced by the electron tunneling processes between the SSH single-chain and the two leads. To understand the dependence of the energy spectrum of the SSH single-chain on the magnitude of the tunneling coupling strength, we here consider the energy spectrum of the SSH single-chain coupled to the two nearest-neighbor lattices of the left and right leadsj=−1 andj=1. When the SSH single-chain weakly coupled to the two leads, the magnitude of the tunneling coupling strength has a slight influence on the energy spectrum of the SSH singlechain.Consequently,the positions of the two transmission resonance peaks in the vicinity of the zero energy correspond to the energy levels of the two non-trivial topological edge states,see the solid lines in Fig. 3(b). However, the magnitude of the tunneling coupling strength will have a significant influence on the energy spectrum of the SSH single-chain when the SSH single-chain strongly coupled to the two leads. Particularly, the energy levels of the two non-trivial topological edge states will disappear,see the dashed lines in Fig.3(b),as a results the transmission probability approaches zero,see the short-dash-dotted line in Fig. 3(a). Therefore, the number of transmission resonance peaks associated with the non-trivial topological edge states will be reduced from two to zero with increasing the strength of tunneling coupling between the SSH single-chain and the two leads from the weak to the strongcoupling regimes. These results suggest an alternative way to detect whether the SSH single-chain is of the non-trivial topological edge states or not. Fig. 3. (a) The transmission probabilities of electron transport through the SSH single-chain in the vicinity of the zero energy as a function of the energy of incident electron for different strengths of tunneling coupling tL=tR.(b) Energy spectrum of the SSH single-chain coupled to the two nearestneighbor lattices of the left and right leads j=−1 and j=1 in the vicinity of the zero energy with tL=tR=0.00001 and tL=tR=0.001. The parameters of the SSH single-chain are chosen as υ =0.4,w=1.0,and N=10. In a ring-shaped SSH double-chain system, the conduction electrons from the source electrode have two different paths of the upper and lower chains tunnel out the SSH system and tunnel into the drain electrode finally. Consequently,we can study the influence of the quantum interference between the two different electron tunneling paths on the electron transport properties of the non-trivial topological edge states.Here,we discuss the two cases,namely,the ring-shaped SSH double-chain with the upper chain being different from the lower one,and that with the upper chain being the same as the lower one. In the former case, we consider the two types of ring-shaped SSH double-chain,namely,the length of upper chain being the same as the lower one but with different intracell hopping amplitude, and the intra-cell hopping amplitude of the upper chain being the same as the lower one but with different length. In the first type of ring-shaped SSH double-chain with the upper chain being different from the lower one,we chooseυ1=0.4,υ2=0.5,andN1=N2=10. When the ring-shaped SSH double-chain weakly coupled to the two leads,the transmission probability displays the four resonance peaks in the vicinity of the zero energy, see the solid and the dashed lines in Fig. 4(a). Here, the positions of the two middle resonance peaks correspond to that of two resonance peaks of the SSH single-chain withυ=0.4,while the positions of the two other resonance peaks correspond to that of two resonance peaks of the SSH single-chain withυ=0.5. When the tunneling coupling strengthtL=tRis increased gradually, the width of the four resonance peaks will be broadened,and the positions of the first peak on the left and that of the first peak on the right will move towards the zero energy position,and the two middle resonance peaks will especially evolve into a relatively wide resonance peak, see Fig. 4(b). Interestingly, when the tunneling coupling strengthtL=tRreaches at a certain value,the width of the first peak on the left and that of the first peak on the right will become narrower and form two sharp peaks finally, whereas the relatively wide resonance peak evolved from the two middle resonance peaks will disappear gradually,see Fig.4(c). Fig.4. The transmission probabilities of electron transport through the ringshaped SSH double-chain in the vicinity of the zero energy as a function of the energy of incident electron for different strengths of tunneling coupling tL =tR. The parameters of the ring-shaped SSH double-chain are chosen as υ1=0.4,υ2=0.5,w=1.0,and N1=N2=10. Fig.5. Energy spectrum of the ring-shaped SSH double-chain coupled to the two nearest-neighbor lattices of the left and right leads j =−1 and j =1 in the vicinity of the zero energy with w=1.0. (a1)tL =tR =0.00001 and N1=N2=10. (b1)tL=tR=1.0 and N1=N2=10. (a2)tL=tR=0.00001,N1=10 and N2=11. (b2)tL=tR=1.0,N1=10 and N2=11. To illustrate the physical mechanism of the transmission resonance peaks, we also consider the energy spectrum ofthe ring-shaped SSH double-chain coupled to the two nearestneighbor lattices of the left and right leadsj=−1 andj=1.In the weak coupling regime,e.g.,tL=tR=0.00001,the four energy levels in the vicinity of the zero energy correspond to the positions of the four transmission resonance peaks, see Figs.4(a)and 5(a1). Whereas in the strong coupling regime,e.g.,tL=tR= 1.0, the two energy levels in the vicinity of the zero energy correspond to the positions of the two transmission resonance peaks, see Figs. 4(c) and 5(b1), which is different from the case of the SSH single-chain. To further determine that whether the eigenstates of these energy levels in the vicinity of the zero energy is of the non-trivial topological edge states or not, it is necessary to investigate the distribution of probability amplitudes of the wave functions of these nearly zero-energy eigenstates. In the weak coupling regime,the distribution of probability amplitudes of the wave functions of the four nearly zero-energy eigenstates display the characteristics of non-trivial topological edge states, namely,the first and last sublattices of the upper and lower chains have the maximum magnitudes of probability amplitudes, respectively, and the magnitude of the probability amplitudes exponentially decays from the two ends to the middle of the upper(lower)chain,see Figs.6(a1)–6(d1). While in the strong coupling regime,the wave functions of the two nearly zero-energy eigenstates are also exponentially localized at the two ends of the upper and lower chains, see Figs. 7(a1) and 7(b1). This characteristic indicates that the first type of ring-shaped SSH double-chain strongly coupled to the two leads still has two non-trivial topological edge states. While in the second type of ring-shaped SSH doublechain,we chooseυ1=υ2=0.5,N1=10,andN2=11. In the vicinity of the zero energy,with increasing the tunneling coupling strength from the weak to the strong coupling regimes,the variation of the transmission resonance peaks is the same as that in the first type of ring-shaped SSH double-chain, see Fig.8. Moreover,the positions of the transmission resonance peaks in the weak and strong coupling regimes also correspond to the energy levels of the ring-shaped SSH double-chain coupled to the two nearest-neighbor lattices of the left and right leadsj=−1 andj=1,see Figs.8,5(a2),and 5(b2). Importantly,the wave functions of the four nearly zero-energy eigenstates in the weak coupling regime and that of the two nearly zero-energy eigenstates in the strong coupling regime are also exponentially localized at the two ends of the upper and lower chains,see Figs.6(a2)–6(d2),7(a2),and 7(b2). Consequently,the second type of ring-shaped SSH double-chain in the weak and strong coupling regimes also has the four and two nontrivial topological edge states,respectively. Fig.6. The distribution of probability amplitudes of the wave functions of the four nearly zero-energy eigenstates of the ring-shaped SSH double-chain coupled to the two nearest-neighbor lattices of the left and right leads j=−1 and j=1 with w=1.0 and tL =tR =0.00001. (a1)–(d1), υ1 =0.4,υ2=0.5,and N1=N2=10. (a2)–(d2),υ1=υ2=0.5,N1=10,and N2=11. Fig. 7. The distribution of probability amplitudes of the wave functions of the two nearly zero-energy eigenstates of the ring-shaped SSH double-chain coupled to the two nearest-neighbor lattices of the left and right leads j=−1 and j=1 with w=1.0 and tL=tR=1.0. (a1)and(b1)υ1=0.4,υ2=0.5,and N1=N2=10. (a2)and(b2)υ1=υ2=0.5,N1=10,and N2=11. We last discuss the case of the upper chain being the same as the lower one,and chooseυ1=υ2=0.4 andN1=N2=10.In the vicinity of the zero energy, the transmission probability in the weak coupling regime displays the two resonance peaks only, see Fig. 9(a), which is different from the case of the upper chain being different from the lower one, see Figs. 4(a) and 8(a). Particularly, the two transmission resonance peaks will disappear gradually by increasing the tunneling coupling strength from the weak to the strong coupling regimes,see Fig.9(a).These characteristics can also be understood in terms of the energy spectrum of the ring-shaped SSH double-chain coupled to the two nearest-neighbor lattices of the left and right leadsj=−1 andj=1. In the weak coupling regime,the energy spectrum of the system have the two twofold-degenerate energy levels in the vicinity of the zero energy, see the dashed and the dotted lines Fig. 9(b), thus the two corresponding transmission resonance peaks is found.Whereas in the strong coupling regime, although the energy spectrum of the system has two non-degenerate energy levels in the vicinity of the zero energy,see the dash-dotted lines Fig.9(b),the transmission resonance peak can not found.This characteristic indicates that the disappearance mechanism of the transmission resonance peaks can be attributed to the destructive interference between the two different electron tunneling paths of the upper and lower chains. Therefore, in the ring-shaped SSH double-chain coupled to the two leads, with increasing the tunneling coupling strength from the weak to the strong coupling regimes, the number of transmission resonance peaks in the vicinity of the zero energy will be reduced by two. For example,in the case of the upper chain being different from the lower one,the number of transmission resonance peaks will be reduced from four to two; whereas that will be reduced from two to zero in the case of the upper chain being the same as the lower one.These results suggest an alternative way to detect whether the ringshaped SSH double-chain system is of the non-trivial topological edge states or not. Fig.8. The transmission probabilities of electron transport through the ringshaped SSH double-chain in the vicinity of the zero energy as a function of the energy of incident electron for different strengths of tunneling coupling tL =tR. The parameters of the ring-shaped SSH double-chain are chosen as υ1=υ2=0.5,w=1.0,N1=10,and N2=11. Fig. 9. (a) The transmission probabilities of electron transport through the ring-shaped SSH double-chain in the vicinity of the zero energy as a function of the energy of incident electron for different strengths of tunneling coupling tL=tR.(b)Energy spectrum of the ring-shaped SSH double-chain coupled to the two nearest-neighbor lattices of the left and right leads j=−1 and j=1 with tL =tR. The parameters of the ring-shaped SSH double-chain system are chosen as υ1=υ2=0.4,w=1.0,and N1=N2=10. We have studied the transmission probability of electron transport through the ring-shaped SSH double-chain system in the vicinity of the zero energy. We have demonstrated that the positions of transmission resonance peaks in the vicinity of the zero energy correspond to the energy levels of the non-trivial topological edge states. In particular, the quantum interference between the two different electron tunneling paths of the upper and lower chains has a significant influence on the num-ber of transmission resonance peaks associated with the nontrivial topological edge states. For example,in the case of the upper chain being different from the lower one, the electron transmission probability displays the four and two resonance peaks in the weak and strong coupling regimes, respectively;whereas in the case of the upper chain being the same as the lower one, the electron transmission probability displays the two transmission resonance peaks in the weak coupling regime only, and the transmission resonance peak disappears in the strong coupling regime that originated from the destructive interference between the two different electron tunneling paths of the upper and lower chains. The predicted properties of the variation of the number of transmission resonance peaks associated with the non-trivial topological edge states in the weak and strong coupling regimes suggest an alternative way to detect whether the ring-shaped SSH double-chain system is of the non-trivial topological edge states or not. Acknowledgments Project supported by the National Natural Science Foundation of China (Grant No. 11974153), the Natural Science Foundation of Shanxi Province, China (Grant No. 20210302123184), the Program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi Province, China (Grant No. 163220120-S), and the Natural Science Foundation of Shandong Province, China (Grant No.ZR2020MA091).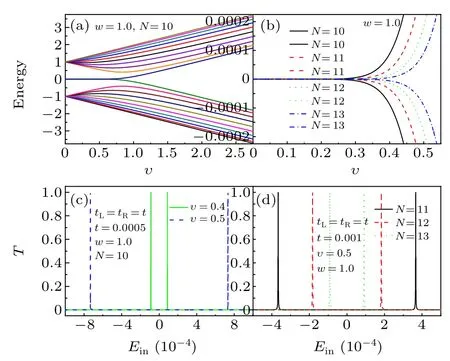
3.2. Detecting non-trivial topological edge states of the SSH single-chain

3.3. Detecting non-trivial topological edge states of ringshaped SSH double-chain


4. Conclusion
- Chinese Physics B的其它文章
- High sensitivity plasmonic temperature sensor based on a side-polished photonic crystal fiber
- Digital synthesis of programmable photonic integrated circuits
- Non-Rayleigh photon statistics of superbunching pseudothermal light
- Refractive index sensing of double Fano resonance excited by nano-cube array coupled with multilayer all-dielectric film
- A novel polarization converter based on the band-stop frequency selective surface
- Effects of pulse energy ratios on plasma characteristics of dual-pulse fiber-optic laser-induced breakdown spectroscopy