Darboux transformation and soliton solutions of a nonlocal Hirota equation

Yarong Xia(夏亚荣), Ruoxia Yao(姚若侠), and Xiangpeng Xin(辛祥鹏)

1School of Computer Science,Shaanxi Normal University,Xi’an 710062,China

2School of Information and Engineering,Xi’an University,Xi’an 710065,China

3School of Mathematical Sciences,Liaocheng University,Liaocheng 252029,China

Starting from local coupled Hirota equations,we provide a reverse space-time nonlocal Hirota equation by the symmetry reduction method known as the Ablowitz–Kaup–Newell–Segur scattering problem.The Lax integrability of the nonlocal Hirota equation is also guaranteed by existence of the Lax pair.By Lax pair,an n-fold Darboux transformation is constructed for the nonlocal Hirota equation by which some types of exact solutions are found.The solutions with specific properties are distinct from those of the local Hirota equation.In order to further describe the properties and the dynamic features of the solutions explicitly,several kinds of graphs are depicted.

Keywords: nonlocal Hirota equation,Darboux transformation,Lax pair,soliton soultion

1.Introduction

Recently, research of nonlocal equations has become a hot topic in nonlinear sciences involving quantum theory,nonlinear optics, etc.[1–6]The research on integrability of nonlocal equations not only can enrich the theory of integrable systems, but also can be used to explain the complex phenomena that occur in multi-place systems,for example,establishing the relationship between the position(x,t)and(−x,t)through nonlocal models, and exploring physical phenomena such as quantum entanglement.[7–9]For the abundant nonlocal equations, the most important equation is nonlocal nonlinear Schrdinger(NNLS)equation[10]

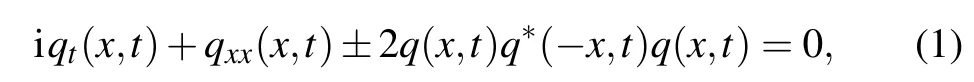
which was proposed by Ablowitz and Musslimani.Here,q∗denotes the complex conjugation ofq.Equation(1)is nonlocal asqis a function of not only(x,t)but also(−x,t),which is the case of parity reversal.The Lax pair and conservation law of Eq.(1) have been given in Ref.[10], which indicates that Eq.(1) is an integrable system.These interesting results enrich the range of integrable systems and provide a method to find more integrable equations.What’s more, Eq.(1) has some special properties different from the classic NLS equation, so it has attracted great attention from the researchers.On the one hand,some researchers have been devoted to generalizing nonlocal Schrdinger Eq.(1),and proposed the nonlocal Schrdinger equation for time reversal, space-time reversal simultaneously and the discrete nonlocal Schrdinger equation.[11–15]On the other hand, some new nonlocal nonlinear equations have also been proposed by using symmetry reduction method.[16–20]For these new nonlocal equations,the integrability and exact solutions are studied with the method of inverse scattering, Darboux transformation and the Hirota bilinear transformation,etc.,and the results show that the nonlocal equation possesses new features which are different from the corresponding local equation.

This paper,inspired by the study of nonlocal Schrdinger equation in Ref.[10],deduces the reverse space-time nonlocal Hirota equation

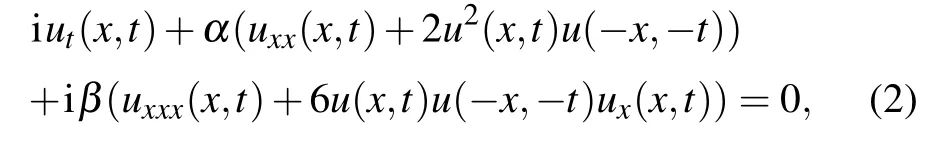
by a symmetry reduction method.Furthermore, we construct a Darboux transformation and present several types of explict solutions for Eq.(2).

The rest of the paper is organized as follows: In Section 2,the nonlocal Hirota equation is deduced by the method of symmetry reduction, and the lax integrability of the equation is guaranteed.In Section 3, the Darboux transformation of Eq.(2) is constructed, and then ann-fold Darboux transformation formula is provided.In Section 4,the soliton,kink,antikink and interaction solutions to Eq.(2) are acquired via the Darboux transformation.A short conclusion and discussion is included in Section 5.

2.Integrable nonlocal Hirota equation

The well-known Hirota equation has the following form:[22]

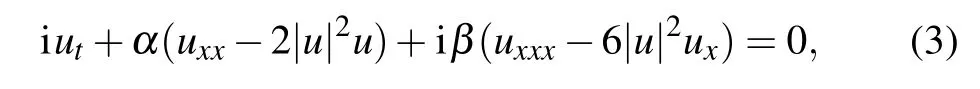
where α and β are real constants.When α=1,β =0,Eq.(1)is transformed into a general NLS equation.

According to the ideas given by Ablowitz, if we want to construct a nonlocal equation,we must start from a pair of coupled equations.Therefore,we consider the following coupled Hirota equation:

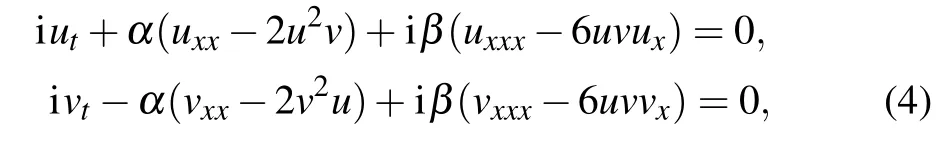
which can be reduced to Eq.(1)whenu=−v∗,andv∗denotes the complex conjugate ofv.The linear spectral problem(i.e.,Lax pair)of Eqs.(4)is expressed by[23]

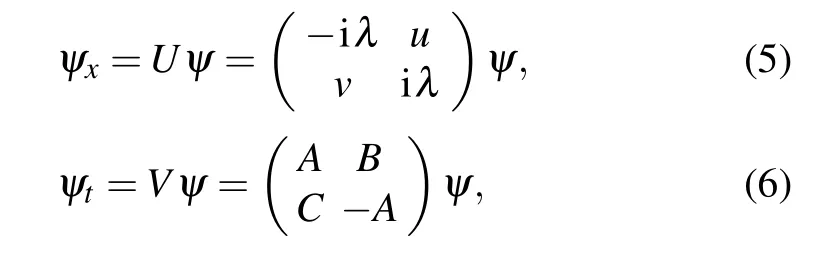
with

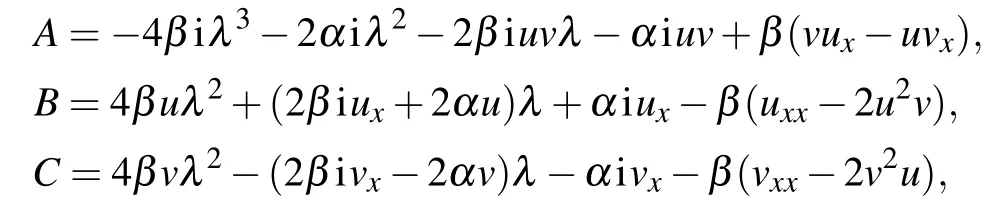
where

Using the following condition:

Ut−Vx+[U,V]=0,

we can transform Eqs.(5)and(6)to Eq.(4).Through observation,we find that the structures of the two equations(4)are very similar.Then, using the idea of Ablowitz, we adopt the following symmetry transformation,

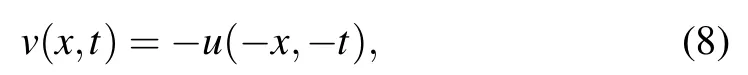
and substitute Eq.(8)into the system(4)to derive the nonlocal Hirota equation

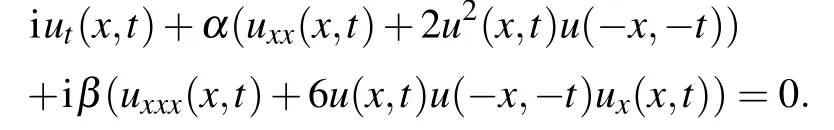
Lax pair of the nonlocal Hirota equation is then obtained from Eqs.(4)with the help of Eq.(8),which implies that the nonlocal Hirota equation is Lax integrable.Then,we can construct Darboux transformation for Eq.(2)by Lax pair.

3.Darboux transformation of the nonlocal Hirota equation

Darboux transformation (DT) is one of the important method to construct exact solutions of local equations.[18]Of course,this method has also been widely employed to find exact solutions of nonlocal equations.[19,24–26]This section will be devoted to the study of DT of the newly obtained nonlocal equation(2).

3.1.One-fold DT

The basic idea of DT is to construct a transformation that can keep the spectrum problem unchanged.Consider the following gauge transformation:

and require ψ[1]satisfying the following equations:

Considering the transformation(9)and the conditions(10),the spectral problem (5) and (6) can be transformed into the following new forms:

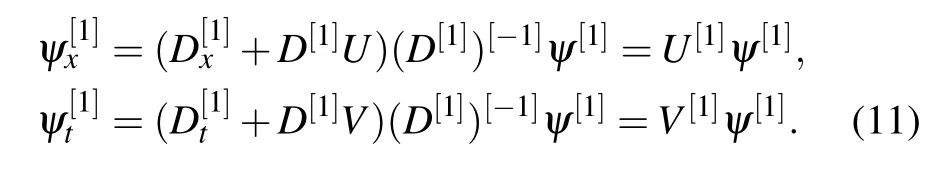
From the expressions(11), it is essential to construct the matrixD[1]to makeU[1]andU,V[1]andVin same forms,except the difference between the old and new potential functions.

In order to get the concrete form of the gauge transformation,it is necessary to make an appropriate assumption

withC[1]=,andIis two-order identity matrix.The following work is to construct the form ofC[1].By substituting Eq.(12)into Eq.(11), and making a comparison with coefficients of λm,we get the following relationships between the new and the old potential functions:

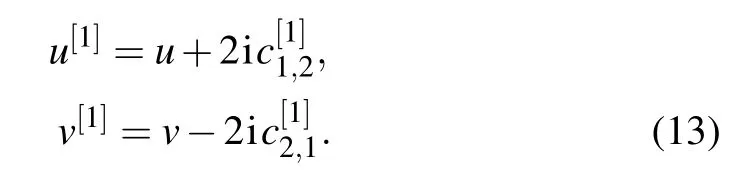
Using the symmetry transformation(8),we derive the following constraint condition:

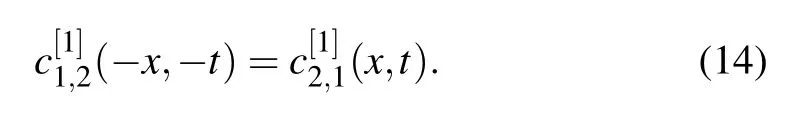
To proceed, we need to determine the concrete form ofD[1].Let

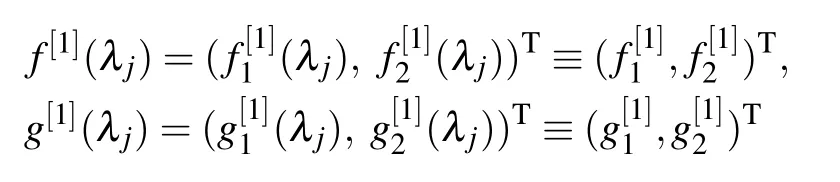
be eigenfunctions of the lax pair(5)and(6)with λ=λj(j=1,2).From the gauge transformation(9),we obtain the following equations:

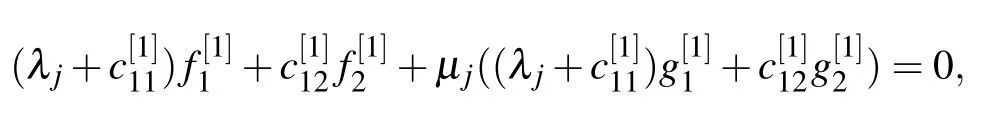
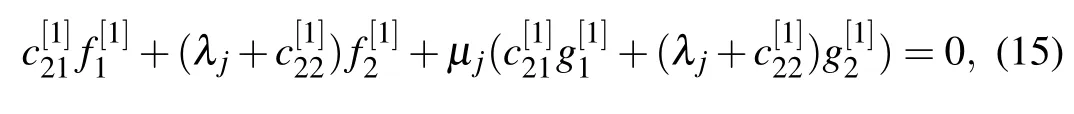
whereµj(j=1,2)are constants.Equations(15)can be transformed into the following linear algebraic system:

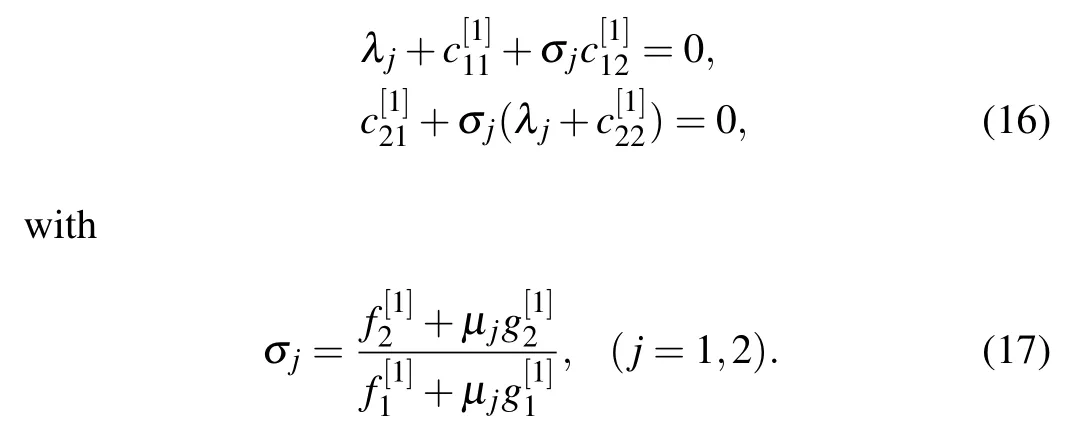
Choose suitable constants λj,µjto ensure the coefficients of the determinant of Eq.(16)to be nonzero, thencan be uniquely determined.From Eq.(12), we can derive the following matrixD[1]:

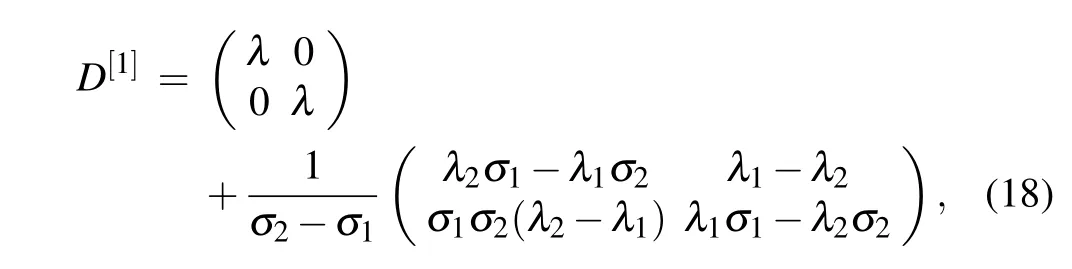
where σ1and σ2satisfy the following identities:

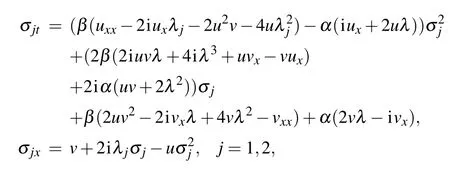
andv(x,t)=−u(−x,−t).

Next,U[1]andU,V[1]andVwill be proved with the same forms.

As

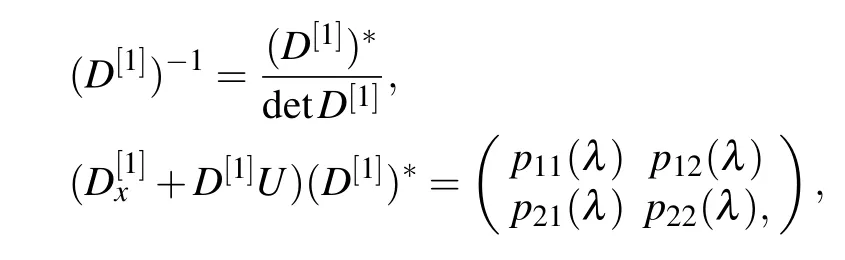
after direct but tedious calculations, we know thatpij(λ) (i,j=1,2)are polynomials of λ,and the highest power of them are quadratic or cubic.The spectral parameters λj(j=1, 2)can be proved to be the roots ofpi j(λ) (i,j=1, 2) with the help of Eqs.(14).Because λj(j=1, 2)are also the roots of detD[1],we obtain the following identities:

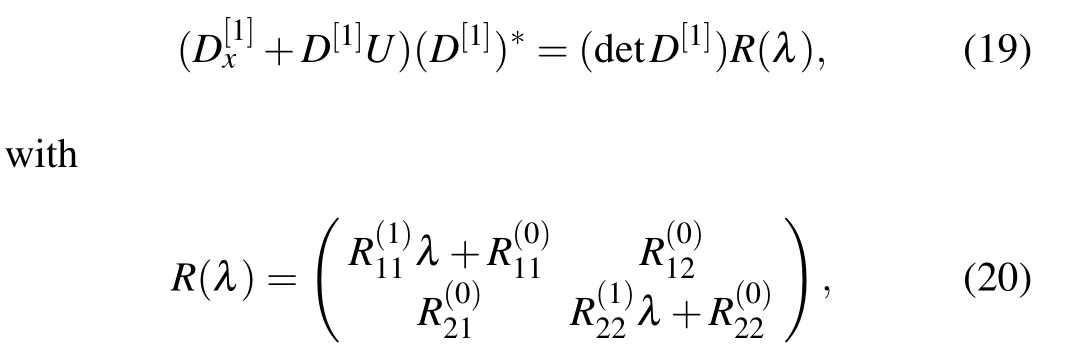
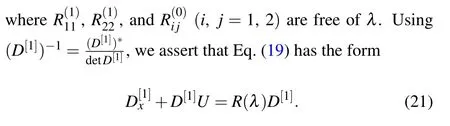
The comparison of the coefficients of the same powers of λ in Eq.(21)leads to the following equations:

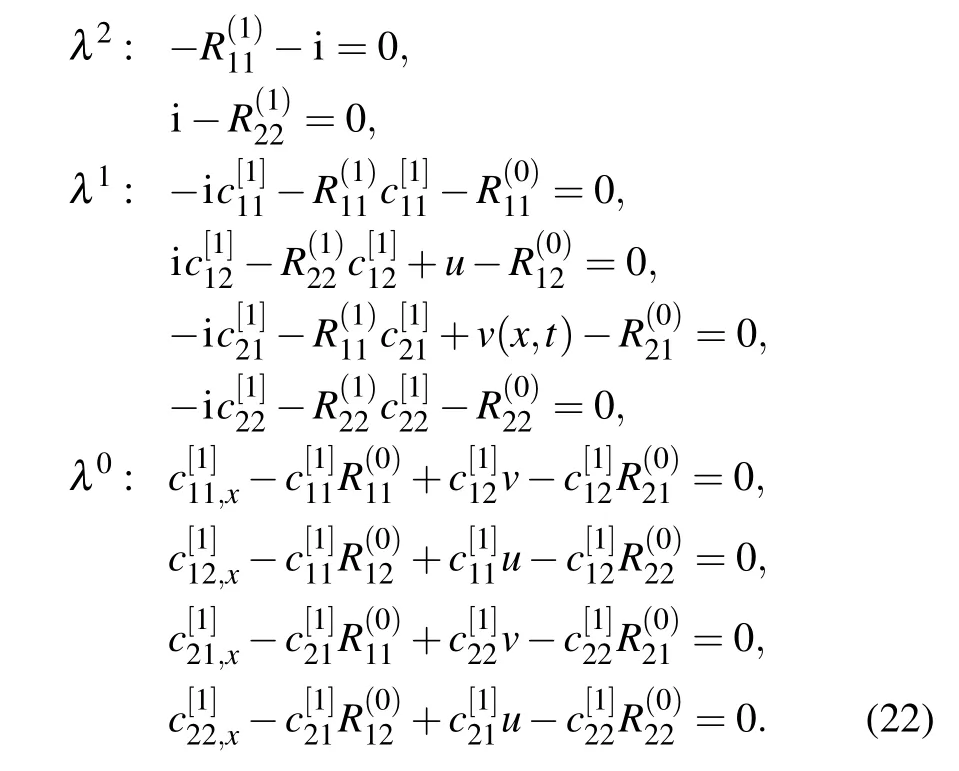
By solving the overdetermined system (22) with the help of Eqs.(13),we obtain

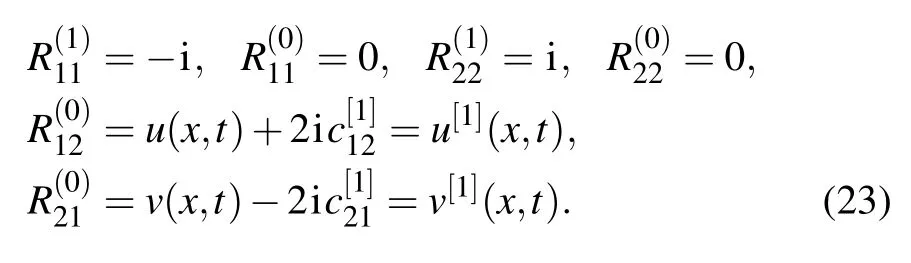
That is to say,

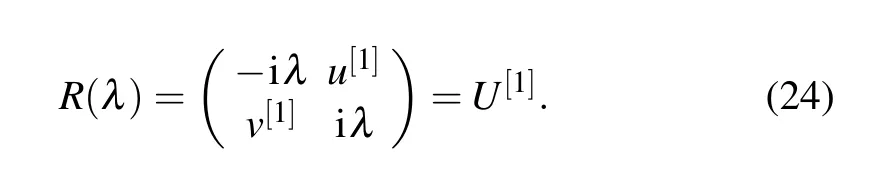
Similarly,we can also illustrate thatV[1]andVare in the same form as

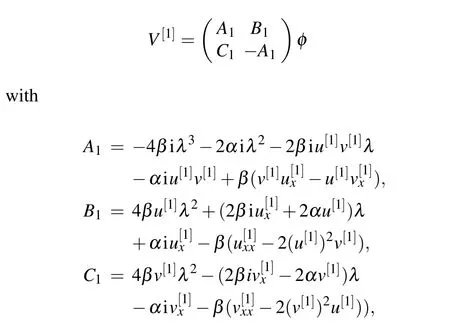
where the relationships ofuandu[1],vandv[1]are determined by Eq.(13).

3.2.Two-fold DT

To discuss the 2-fold DT of Eq.(2),we suppose that

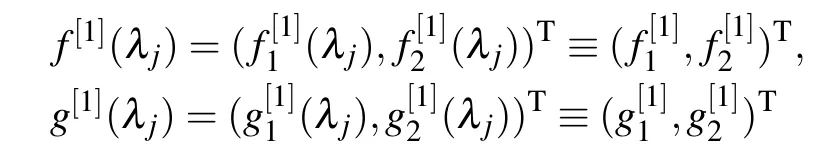
are solutions of Eqs.(5) and (6) at λ =λ3, λ =λ4withu[0].Employing the one-fold DT,we derive

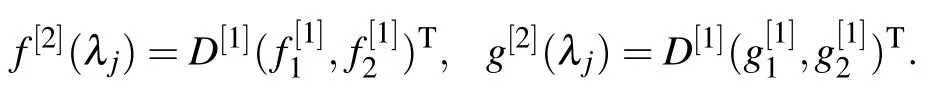
Next,similar to 1-fold DT,2-fold DT can be established as

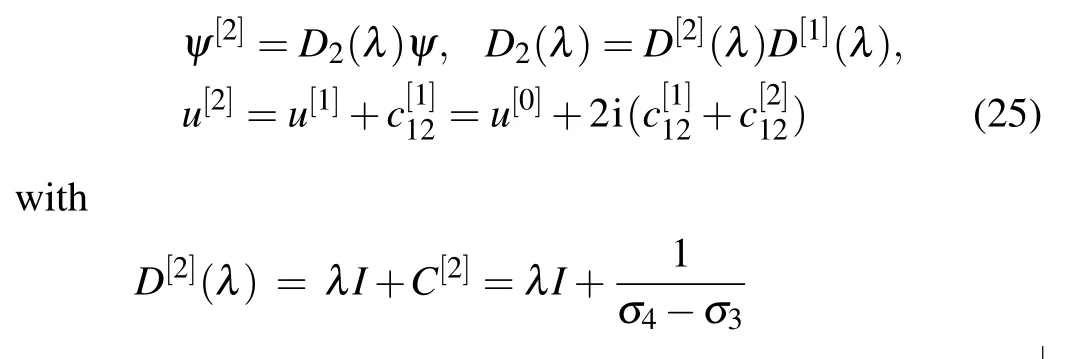
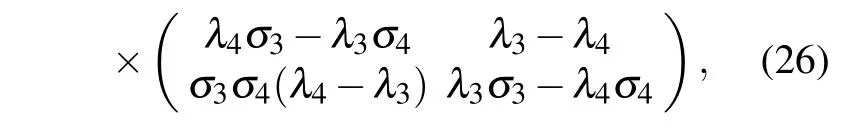
and

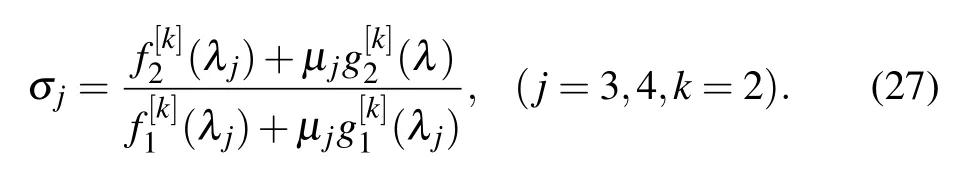
3.3.N-fold DT

Furthermore,ann-fold DT for the nonlocal Hirota Eq.(2)can be derived by the above iteration process,and

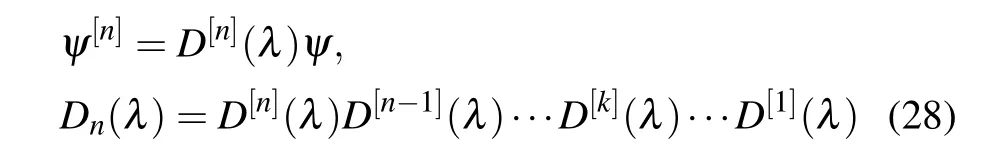
with

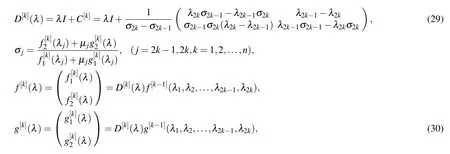
the matrixC[k]satisfies

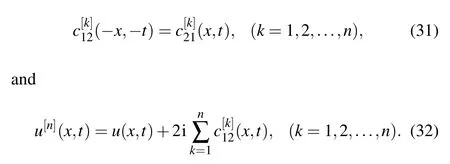
The above results show that the construction process of the DT for local and nonlocal Hirota equation is similar, and the higher order DT formula of them can be obtained through multiple iterations.However, the existence of the constraint condition leads to big difference for these two cases.

4.Soliton solutions of the nonlocal Hirota equation

Soliton solutions have been studied well for various nonlinear systems.[27–29,31–36]This section aims to construct exact solutions to nonlocal Hirota Eq.(2) by Darboux transformation.

4.1.One soliton solutions

We can obtain one-soliton solutions to Eq.(2)from a seed solutionu=v=0.By solving the spectral problem(5)and(6),we obtain the following eigenfunctions about λ =λj,(j=1,2,...,n):

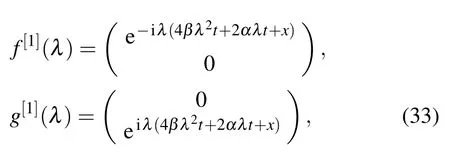
and by the expression(17),we have

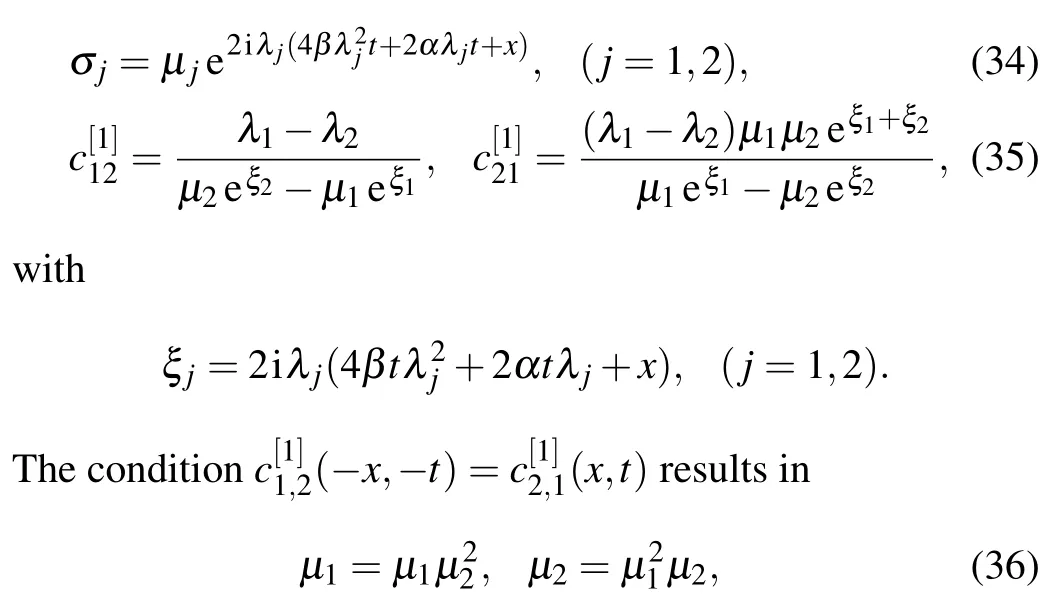
Case 1µ1=−1,µ2=1.

Through Eq.(32),the following new solution is obtained

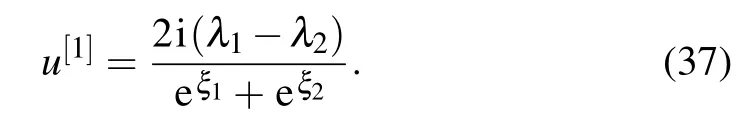
To ensure that there do not exist singular points in the solution,we require that the expression

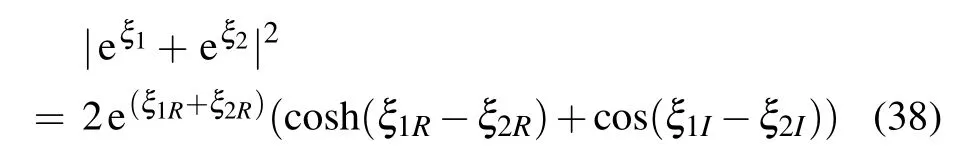
is nonzero, here λj=κj+iωj, κj,ωjare are real numbers,and

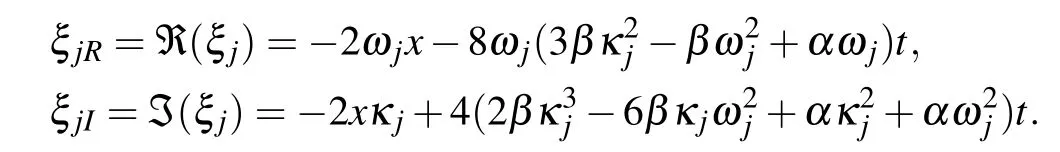
In order to make equation(38)unequal to zero,the λj(j=1,2)must satisfy the following two conditions:

(a) (ω1+ω2)α+2β[ω1(2κ1+κ2)+ω2(κ1+2κ2)]=0,(b) ω1=ω2and

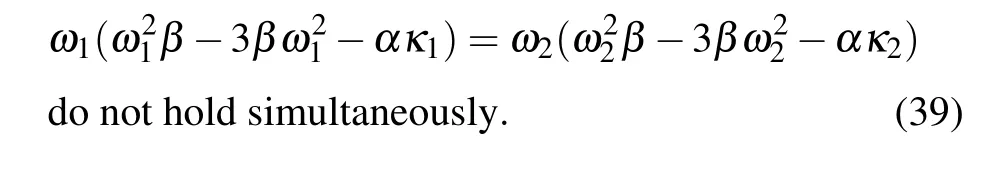
Next,we discuss some special one-soliton solutions according to Eq.(37)and conditions(39).

(1)Take κ1=κ2and ω1=−ω2,then ξ1R+ξ2R=0 holds for all(x,t)∈R2, and satisfies the conditions(39).A typical soliton solution can be derived as follows:

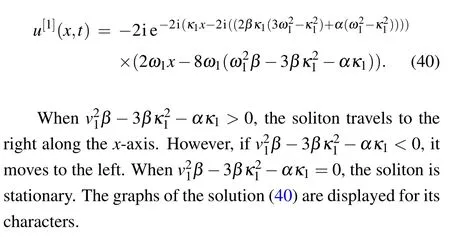
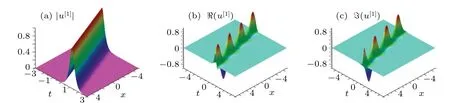
Fig.1.(a)Evolutionary graph of Eq.(40)with parameter κ1=,ω1=,α =1,β =−1 and −ακ1>0.(b)The images of the real part of the solution.(c)The imaginary part of the solution.

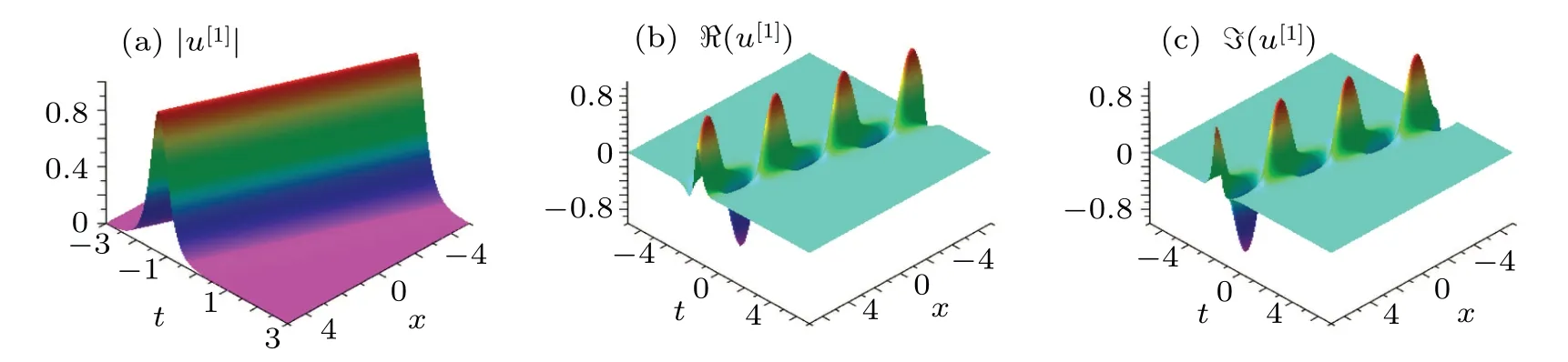
Fig.2.(a)Evolutionary graph of Eq.(40)with parameter κ1 =,ω1 =,α =−1,β =1,and −ακ1 <0.(b)The images of the real part of the solution.(c)The imaginary part of the solution.

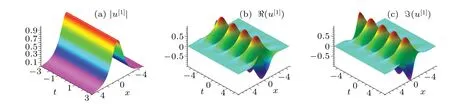
Fig.3.(a)Stationary graph of Eq.(40)withµ1=,v1=,α =−1,β =−1,and −ακ1=0.(b)The images of the real part of the solution.(c)The imaginary part of the solution.

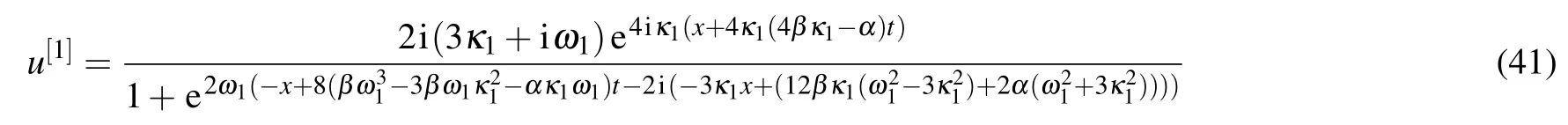
(2)Take ω2=0,κ2=−2κ1,then ξ2R=0 holds for all(x,t)∈R2,and the complexiton solution can be derived.From the solution (41), we find that if ω1<0, the complexiton travels like a kink wave, and it presents the antikink shape if ω1>0.Similarly,the soliton propagates to the right of thex-axes when−ακ1>0,and to the left if−ακ1<0.While as−ακ1=0,the soliton is stationary.,ω1=−3,α =,β =−2.(b)The images of the real part of the solution.(c)The imaginary part of the solution.,ω1=3,α =,β =−2.(b)The images of the real part of the solution.(c)The imaginary part of the solution.

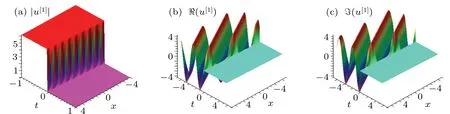
Fig.4.(a)Structure of solution(41)with parameter κ1=

Fig.5.(a)Structure of solution(41)with parameter κ1=

Case 2µ1=µ2=1 orµ1=µ2=−1.

Similar to the analysis of Case 1,we derive the following solution

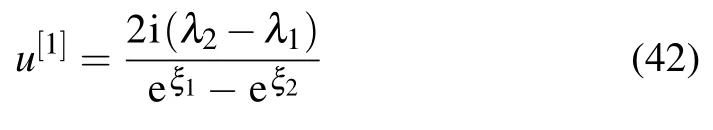
from the expression(42).It shows that when(x,t)satisfies the following equation:

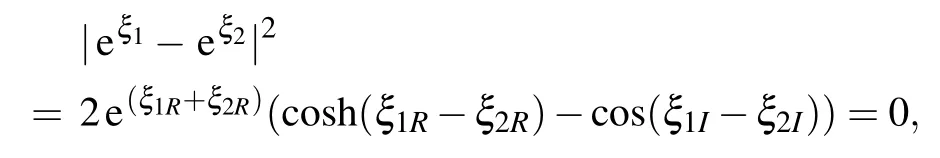
that is,

cosh(ξ1R−ξ2R)−cos(ξ1I−ξ2I)=0,

i.e., ξ1R−ξ2R=0, ξ1I−ξ2I=2kπ, the solution (42) has infinitely many singular points.

Likewise,one can also discuss the following three cases:µ1=1,µ2=−1;µ1=i,µ2=−i;andµ1=−i,µ2=i.

4.2.Two-soliton solutions

This section gives two-soliton solutions of the nonlocal Hirota equation with the 2-fold DT.Firstly, using Eq.(26)with the help of Eq.(30), we can determine.Considering the condition, we obtain the relationships=1,=1.To meet the above condition, we take µ1=−1, µ2=1, µ3=−1, µ4=1.Next,the following two different types of interaction solutions will be considered through taking different eigenvalues.

(1) Interaction solutions between bright and bright solitons.

The eigenvalues are conjugate complex numbers, λ1==κ1+iω1, λ3==κ2+iω2, then through Eq.(32),u[2]is derived as follows:

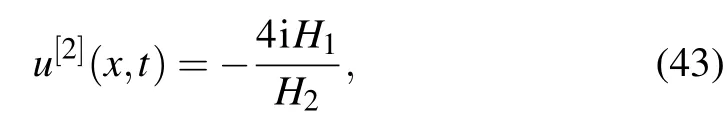
where

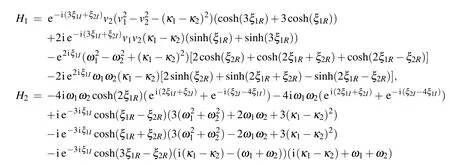
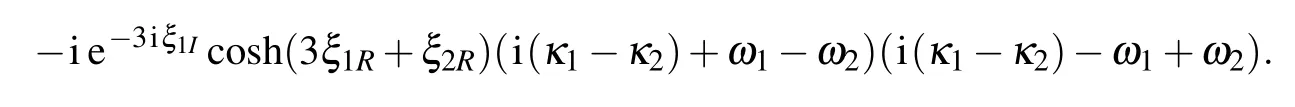
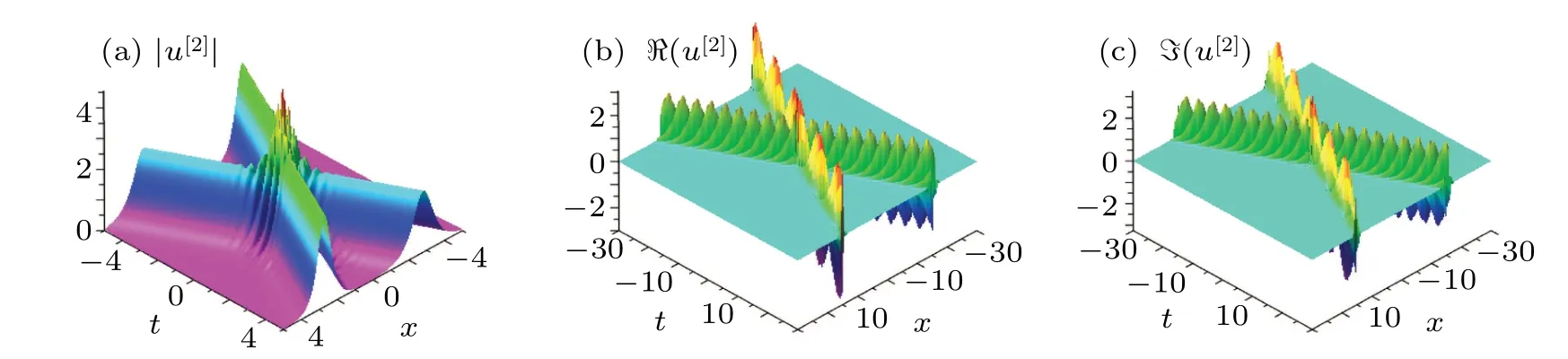
Fig.6.(a)The interaction of bright-bright soliton(43)with parameter

The corresponding graphs for soliton(43)are given in Fig.6..(b)The images of the real part of the solution.(c)The imaginary part of the solution.

From Fig.6, we find that the propagation velocities and directions of two solitons have not changed while the phase shift of every soliton is accompanied with each other,and the interaction solution shows the elastic collision quality.

(2)Interaction solutions between kink and bright solitons.

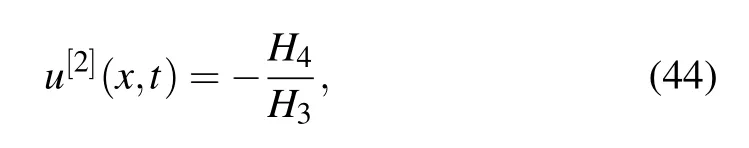
where

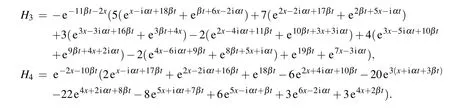
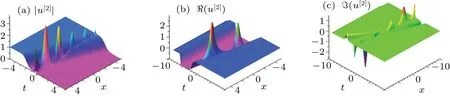
Fig.7.(a)The interaction of kink and soliton solution(29)with parameter

The corresponding graphs for Eq.(44)are given in Fig.7..(b)The images of the real part of the solution.(c)The imaginary part of the solution.

From Fig.7,we find that before and after interaction,the kink is still kink only with phase shifts and the soliton remains the same.However, the background wave of the soliton changes from zero background wave before the collision to nonzero background wave after the collision.

5.Summary and discussion

This paper presents a reverse space-time integral nonlocal Hirota equation by the symmetry reduction method and constructs the Darboux transformations of the equation.Next,we investigate special exact solutions from the corresponding one and two-fold DT, including soliton, kink, antikink and interaction solutions.Furthermore,we depict the graphs of soliton solutions,and illustrate the dynamical behavior of the obtained solutions.

In many aspects of research on nonlocal equations, constructing exact solutions for nonlocal equations is a very meaningful work.There are many methods for studying exact solutions of nonlocal equations, and each method has its own advantages and disadvantages.The DT is a valid approach to construct multi-soliton solution of nonlocal equations,but the premise is that equation must have lax pairs.However, there are some methods that do not need to consider the Lax pair,and can also give birth to rich exact solutions of the nonlocal equation,such as inverse scattering method,Riemann–Hilbert approach, and bilinear method.In the future work, we will consider to use more methods to study nonlocal equations and expect to get some more interesting results.

Acknowledgements

The project was supported by the National Natural Science Foundation of China (Grant Nos.12001424, 11471004,and 11775047), the Natural Science Basic Research Program of Shaanxi Province, China (Grant No.2021JZ-21), the Chinese Post doctoral Science Foundation (Grant No.2020M673332), the Research Award Foundation for Outstanding Young Scientists of Shandong Province, China(Grant No.BS2015SF009), and the Three-Year Action Plan Project of Xi’an University(Grant No.21XJZZ0001-01).