Change-over switch for quantum states transfer with topological channels in a circuit-QED lattice

Liu-Yong Cheng(程留永), Li-Na Zheng(郑黎娜), Ruixiang Wu(吴瑞祥),2,Hong-Fu Wang(王洪福), and Shou Zhang(张寿)

1School of Physics and Information Engineering,Shanxi Normal University,Linfen 041004,China

2Key Laboratory of Spectral Measurement and Analysis of Shanxi Province,Shanxi Normal University,Linfen 041004,China

3Department of Physics,College of Science,Yanbian University,Yanji 133002,China

We propose schemes to realize robust quantum states transfer between distant resonators using the topological edge states of a one-dimensional circuit quantum electrodynamics (QED) lattice.Analyses show that the distribution of edge states can be regulated accordingly with the on-site defects added on the resonators.And we can achieve different types of quantum state transfer without adjusting the number of lattices.Numerical simulations demonstrate that the on-site defects can be used as a change-over switch for high-fidelity single-qubit and two-qubit quantum states transfer.This work provides a viable prospect for flexible quantum state transfer in solid-state topological quantum system.

Keywords: quantum states transfer,edge states,change-over switch,circuit quantum electrodynamics(QED)lattice

1.Introduction

Quantum state transfer (QST) between distant nodes is at the heart of quantum information processing and quantum networking.[1–7]Over the past decades,a variety of theoretical and experimental schemes for states transfer have been proposed in different quantum systems.[8–20]Secure and efficient quantum information process usually needs high-fidelity QST,which raises a higher demand to physical systems and operations.Compared with other platforms, the circuit quantum electrodynamics(QED)has attracted substantial attention because of its operability,[21,22]readability,ready fabrication,[23]etc.[24–26]Although the circuit-QED system has many advantages for quantum information processing and quantum computing, the inevitable existence of disorder and disturbance still lead to the decoherence effect of the practical system.

Topological insulators[27–32]are electronic materials,which have a bulk band gap like ordinary insulators but have protected conducting states on their boundaries or surfaces.These conducting edge states are immune to the local disorders and perturbations because of the protection originating from the topological structure of the energy bands.[29,33–37]This makes the topological insulators have many potential applications in quantum information field,[38–46]such as robust QST[38,40,45,46]and topological quantum computing.Meiet al.[38]presented experimentally feasible schemes for realizing robust QST via topologically protected edge states in superconducting qubit chains.Their work studied transfer schemes of single-qubit states and two-qubit entangled states via the topological edge states in different types of qubit chains.Lemondeet al.[46]analyzed the robust acoustic edge states in a two-dimension optomechanical array and realized a state transfer protocol between spin qubits located in distant cavities.However, among various topological systems,the on-site defect is often regarded as a negative factor in the quantum information process.A recent paper[47]researched a switch mechanism of robust QST channel by appropriately introducing the on-site defect on a flux qubit chain.Under the mechanism in Ref.[47],robust single-qubit quantum information transmission or storage can be effectively controlled.

In this paper, we investigate two types of QST with different topologically protected channels in a single onedimensional circuit-QED lattice.By modulating the photon hopping rates and the resonator frequency shift, the onedimensional circuit-QED lattice can be remodeled as a generalized Su–Schrieffer–Heeger(SSH)model,which possesses various topological phases.Then the theoretical analyses exhibit that the transfer of two-qubit quantum state can be realized by using the edge states of the lattice.Subsequent numerical simulation results show high fidelity of QST with the adiabatic evolution conditions.More importantly, via adding on-site defects to different resonators, we find that the distribution of these topological edge states changes accordingly.The changed-edge states can be used as new topologically protected quantum channels to realize robust QST of single-qubit and two-qubit quantum states.We demonstrate that the onsite defects can play the role of change-over switch and steer the lattice into a multifunctional transfer channel with a onedimensional circuit-QED system.

2.System and generalized SSH model

The physical system to consider here is a one-dimensional circuit-QED lattice withNunit cells,as shown in Fig.1.The transmission line resonators (TLR) labeledan,bn,cnform a unit cell,while theN-th unit cell possessesaNandbNwithoutcN.The resonatorsanandbnpossess indirect neighbor interactions.They are both coupled to a tunable superconducting qubitQ1,n,whilebnandcncouple with each other via the superconducting qubitQ2,n.an+1andcnthat belong to two adjacent unit cells are coupled to the qubitQ3,n.Meanwhile,the tunable superconducting qubitsQa,n,Qb,nandQc,nare embedded inside three resonatorsan,bnandcnsuccessively to provide additional control over the frequency shift of the resonator modes with coupling strengthsga,gbandgc.The entire system can be dominated by the Hamiltonian(=1)

whereHfreeis the free Hamiltonian of TLR and superconducting qubits,which can be modeled as

Here,ωi,n(i=a,b,c)and ωqj,n(j=a,b,c,1,2,3)are the frequencies of the TLR and the superconducting qubit.The collective coupling between resonators and the embedded qubits can be defined as

In addition, the last term of Eq.(1) represents the interaction between resonators and two adjacent qubits with coupling strengthgj,

Fig.1.Schematic of 1D circuit-QED lattice.Each unit cell (the rectangle) of the lattice contains three resonators labeled as an, bn and cn.Resonators an,bn and cn contain three superconducting qubits Qa,n,Qb,n and Qc,n,respectively,accompanying with the coupling strengths ga,gb and gc.Two nearest-neighbor resonators an (bn)and bn (cn)in one unit cell couple with each other via an assisted superconducting qubit Q1,n (Q2,n)with the coupling strength g1 (g2).While two resonators cn and an+1 belonging to two unit cells couple with each other via a qubit Q3,n with the coupling strength g3.The dashed circle represents the circuit diagram of the coupling between two indirect adjacent resonators via a superconducting qubit.The energy level space of each qubit can be tuned via magnetic flux provided by a flux-bias line(FBL).

In the rotating frame with respect to the external driving frequency ωdand in the interaction picture with respect to the superconducting qubits frequencies ωq j,n,the Hamiltonian becomes

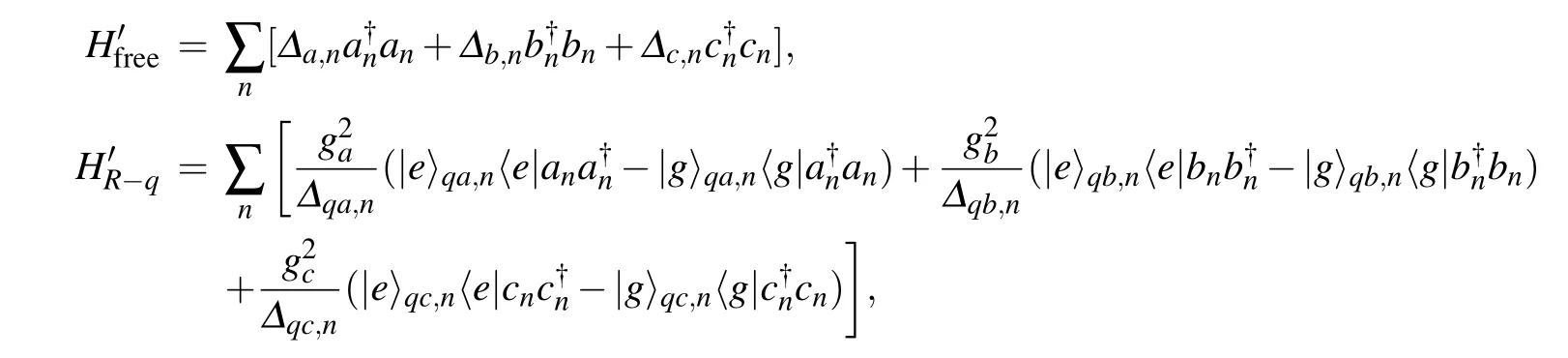
Here Δi,n=ωi,n−ωdis the detuning between the resonator and external driving field, Δq j,n=ωq j,n−ωdrepresents the detuning of the qubits.Under the dispersive regime,[48]if all qubits are prepared in the ground state, the coupling between the qubit and the resonator is removed.After that, the total Hamiltonian can be rewritten as

The first three terms denote the on-site energy of the resonators with qubit-induced resonator frequency shift, the remaining terms represent the coupling between two nearestneighbor resonators assisted by the qubit-mediated photon hopping.[48]Resetting the energy zero point with respect to the resonator detuning(ωi,n−ωd=0),Eq.(6)can be described as

where Δqj,n=ωq j,n−ωd(j=1,2,3,a,b,c) also can be described as Δq j,n=ωq j,n−ωi,n.As we can see,the photon hopping rates and the resonator frequency shift could be directly tuned by changing the qubit detuning Δq j,nvia external control circuits to adjust the qubit frequency ωq j,n.Based on this advantage,each of the coefficients in Eq.(7)becomes modulated.In order to construct a generalized SSH Hamiltonian,we focus on lattice Hamiltonian Eq.(7)confined to the following parameter conditions:

where the parameters θ can be tuned from 0 to 2π.The conditions described in Eq.(8)can be realized by externally tuning the superconducting frequencies as

Generally,the typical qubit level can be modulated in the range of 100 MHz to 15 GHz,[49,50]providing a considerable adjustability in experiment.

Then the effective Hamiltonian becomes This shows that the one-dimensional circuit-QED lattice is constructed as a generalized SSH model, the topological phases are characterized by an integer index — the Chern number.[51]

3.Quantum state transfer channel assisted by topological edge states

In this section, we will demonstrate that two-qubit state transfer can be implemented via topologically protected edge states of the effective model in Eq.(9).The wave function of the edge states can be described as

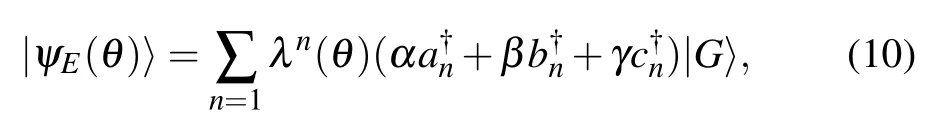
where |G〉=| 0, 0, 0, 0, ..., 0, 0, 0, 0〉.α, β and γ denote the probability amplitudes of the gap state.λ is the localized index.The probability amplitude on resonatorndecays (increases) exponentially when |λ|<1 (|λ|>1), corresponding to the left (right) edge state, if the wave function is normalized.[38,52]Here we take the eigenenergy of an edge state asE.Substituting Eqs.(9) and (10) into Schrdinger equationH′eff|ψE(θ)〉=E|ψE(θ)〉, we can derive the following formulas:

By calculating,the specific wave function of the topological edge state can be obtained,with

We can see that the edge states of this lattice only occupy thea−andb−type resonators.When θ ∈,the corresponding edge state is concentrated toward the left (right) resonators.Particularly, we also find that the edge state is localized in the two leftmost resonators when θ =π/6 or θ =7π/6, and in the two rightmost resonators when θ = π/2 or θ = 3π/2.Under these circumstances, the two leftmost and rightmost resonators are decoupled from the rest of the lattice.The relevant edge states can be expressed as

To verify the correctness of the above analysis, we plot the energy spectrum and the state distribution when the size of the lattice isN=7.In Fig.2(a),there exist one pair of topological edge states labeled as blue and pink.They are separated well from the bulk states.And in Fig.2(b),we observe that the blue edge state is tend to be localized in the two leftmost resonators when θ ∈and in the two rightmost resonators when θ ∈.Note that, the gap state has a peculiar distribution in the two leftmost(rightmost)resonators with the approximately same probability.Apparently,the numerical analysis is consistent with the theoretical results.The distribution of the pink gap state is the same as that of the blue gap state.It provides a foretaste that the system can realize the special state transfer between the left state|L〉and the right state|R〉with θ varying from 0 to 2π.Specially, we take θ(t)=Ωt, with Ω is the gradient describing the variation rate of θ.So, we can achieve the QST via the evolution of the time-dependent Hamiltonian.

Fig.2.Energy spectrum and distribution of the edge states when N=7.Here,we take g j (j=1,2,3,a,b,c)as the energy unit.(a)Energy spectrum of the system.The lattice has a pair of gap states in the gap.(b) Distribution of the blue edge state.When θ ∈[θ ∈],the corresponding edge state is concentrated toward the two leftmost(rightmost)resonators.

Fig.3.Fidelity between the right state |R〉 and the final evolved state versus the varying rate Ω corresponding to different N.Here, we take gj (j=1,2,3,a,b,c)as the energy unit.

To access the quality of this QST,we calculate the fidelity of the state transfer from |L〉 to |R〉 with the varying of Ω corresponding to different sizes of the lattice.The fidelity is defined asF=|〈R|ψ(f)〉|, where |ψ(f)〉 represents the final state governed by the Schrdinger equation and|R〉represents the target state of adiabatic evolution.The simulation results are shown in Fig.3.We observe that the fidelityF>90% can be achieved forN=3.But different lattice lengths with the same Ω will respond differently for the state transfer results.Larger lattice require a smaller Ω to achieve the effective QST.This is because the QST channel is assisted by the edge states of the energy gap and the width of the gap in a generalized SSH model usually exhibits an exponential decay behavior as the system size increases.As a result,corresponding to a large size of the chain, the varying rate of parameter θ should be small to satisfy the adiabatic condition.While the smaller size of the lattice corresponds to a larger energy gap,which means that Ω can take a relatively larger value(adiabatic condition is easier to satisfy).[47]

In order to further prove that our scheme can be implemented under appropriate adiabatic conditions,we prepare the initial state in|Ψi〉=|L〉.The time-dependent state evolution governed bycorresponding to different lattice sizes is shown in Fig.4.We choose Ω = 0.0001 for different lattice lengths in Figs.4(a)–4(c),the images demonstrate that robust two-qubit QST can be realized with the appropriate parameter Ω.By contrast, in Fig.4(d) we choose Ω =0.01 and other conditions are consistent with Fig.4(c),it is straightforward to find that our scheme is completely noneffective.

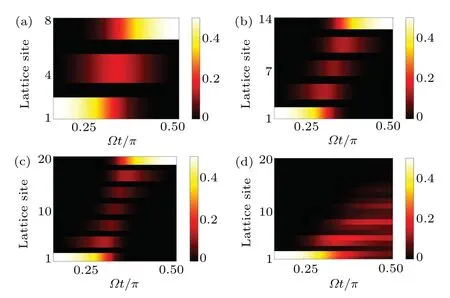
Fig.4.The time-dependent evolution of the left state |L〉 to the right state |R〉 when N takes different values.Here, we take gj (j =1,2,3,a,b,c)as the energy unit.(a)N=3 and Ω =0.0001.(b)N=5 and Ω =0.0001.(c)N=7 and Ω =0.0001.(d)N=7 and Ω =0.01.

4.The defect-induced single-qubit quantum state transfer channel

In Section 3, we have demonstrated that the two-qubit quantum state can be transferred via topological edge states in a 1D circuit-QED lattice.However, in the actual circuit,there are some kinds of random disorder and fluctuations in the physical system.Next, we mainly discuss the fluctuation caused by the on-site defect potential and reveal that it can play an active role in the QST channel.First,we introduce the random on-site defect potential

whereWrepresents the strength of defect potential added on the alli-type resonators of then-th unit cell(i=a,borc).Under the condition of large enough samples of on-site defect,we numerically simulate the fidelity of the QST scheme with on-site defects corresponding to different-type resonators with random strengths in Fig.5.From the curve,we can obtain the following two points.Firstly,the efficiency of the scheme decreases with the increase of the strength of the defect added on thea-orb-type resonators.But for thec-type resonators,there is little impact on the high-efficiency QST.Secondly,with the mild defect strength added on the randomi-type resonator,our scheme can still be achieved with high fidelity.To summarize,thec-type resonators with on-site defects of relatively high strength are more robust than thea- orb-type resonators in our QST scheme.The reason can be obtained from Eq.(12)in which the edge state occupies only thea- andb-type resonators.

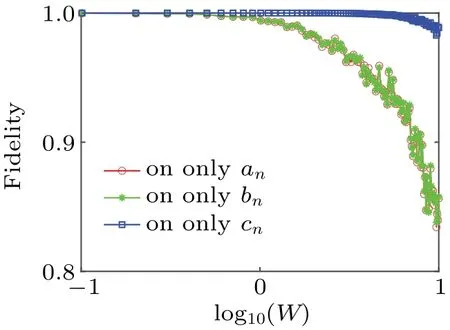
Fig.5.Fidelity between the right state |R〉 and the final evolved state versus the strength of random on-site defect added on different resonators.The red circle line represents the random on-site defects added only on the a-type resonators.The green star line represents the random on-site defects added only on the b-type resonators.The blue squre line represents the random on-site defects added only on the c-type resonators.Here,we take g j (j=1,2,3,a,b,c)as the energy unit.

In Fig.5, we obtain that the on-site defect potentials added ona- orb-type resonators randomly have adverse effects on the QST scheme.In the following, we specifically consider the influence on the system when on-site defects with different strengths are added on the first resonatora1.In this situation,the Hamiltonian of the system can be expressed as

On this basis, we plot the state transfer fidelity as a function of the different on-site defect strength in Fig.6.We observe that the QST channel maintains good working condition with a high fidelity for log10(W)<−0.8,while the channel is totally ineffective with a zero fidelity corresponding to log10(W)>0.These results indicate that our work is robust for mild defect strength and a larger defect potential is added on the first resonator can seriously hamper the implementation of the QST scheme.

To figure out the specific impacts of a larger defect potential for the system, we also plot the relevant energy spectrum with different defect strengths in Fig.7.WhenW=0.1,Fig.7(a)shows that the existence of the on-site defect potential makes the energy spectra slightly deform.The reason is that the presence of the mild defects causes a fluctuation in the energy of the system.But we still can notice that there are two gap states in the energy spectrum.Rather, when the strengthW=10, the band structure and the gap states of the system in Fig.7(b)are quite different from those in Fig.2(b).Apparently,the band structure and the gap states are changed intensively following the growth of the strengthW.That is,a lager defect will steer the first resonatora1decoupled from the initial lattice and change the energy spectrum of the initial system completely.

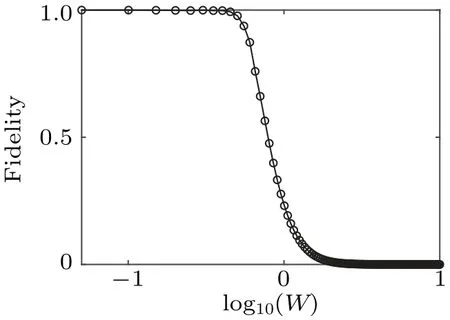
Fig.6.The effects of the on-site defect added on the first resonator on the system.Fidelity between the right state |R〉 and the final evolved state versus the strength of on-site defect added on the first resonator.Here,we take g j (j=1,2,3,a,b,c)as the energy unit.

Fig.7.The effect of the on-site defect added on the first resonator on the system.Here,we take g j (j=1,2,3,a,b,c)as the energy unit.(a)Energy spectrum with W =0.1.(b)Energy spectrum with W =10.The unit cells with N=7.

To unambiguously validate that the distribution of edge states can be adjusted accordingly with the on-site defect added on the first resonator, we make a more detailed analysis of the changed energy spectrum in Fig.8.The state distributions and the corresponding time-dependent evolution of the blue gap state(Fig.7(a))are shown in Figs.8(a)and 8(b).In Fig.7(a) withW=0.1, the numerical results reveal that the blue gap state exhibits a special distribution,in which it is mainly localized near the first resonator when θ =0.83π and θ=1.8π while it is mainly localized at the two leftmost(rightmost)resonators with the same probability at θ ∈(0,0.3π)∪(π,1.3π) (θ ∈(0.3π,0.8π)∪(1.3π,1.8π)).It means we can achieve a new state transfer|0, 0, 0, ..., 0, 0, 0, 0〉→|L〉→|R〉as θ varies from 0.83π to 1.5π.If we set the initial state of the system as|0, 0, 0, ..., 0, 0, 0, 0〉,the corresponding process of the state transfer withis shown in Fig.8(b).This enables us to achieve a simplified two-qubit QST.That is,we can inject a photon in the first resonator and achieve the two-qubit state transfer from|L〉to|R〉.We think this process of preparing a single qubit state, and then evolving to|L〉maybe simpler and more convenient than preparing two-qubit entangled states in the first two resonators directly.In Fig.8(c), the distribution of the edge state forW=0.1 is consistent basically with the initial system under the ideal conditions in Fig.2(b).This is the reason that the fidelity of state transfer in Fig.6 is not affected when the defect strength is relatively small.Figure 8(d)is the corresponding evolution of the initial state|L〉with time-dependent Hamiltonian.

Fig.8.The effects of the on-site defect added on the first resonator on the system.Here, we take gj (j = 1,2,3,a,b,c) as the energy unit.(a), (b) The distribution of the blue gap state with W = 0.1 and the corresponding time-dependent evolution of the initial state |0, 0, 0, ..., 0, 0, 0, 0〉.(c),(d)The distribution of the pink gap state with W =0.1 and the corresponding time-dependent evolution of the initial state |L〉.(e), (f) The distribution of the red gap state with W =10 and the corresponding time-dependent evolution of the initial state |10±| 0, ..., 0, 0, 0, 0〉.(g), (h) The distribution of the green gap state with W =10 and the corresponding time-dependent evolution of the initial state |0, 0, ..., 0, 0, 0, 0〉.Other parameters take N=7 and Ω =0.00001 in(b),(d),(f),and(h).

If considering the greater defect strength withW=10,the distribution and corresponding evolution of the edge states(the red and green gap states in Fig.7(b))shown in Figs.8(e)–8(h)are totally different.Figures 8(e) and 8(f) prove that the red energy gap state can be utilized to construct a new two-qubit QST channel with the new left edge state |L〉new=|10±,..., 0, 0, 0, 0〉to|R〉.Figures 8(g)and 8(h)indicate that another QST channel with|0, 0, ..., 0, 0, 0, 0〉→|0, 0, 0, ..., 0,is generated.

The above results reveal that the large on-site defect added on the first resonator can make the gap state own different distributions, and the different states transfer between the left-and right-edge states can be achieved.Similar results can be obtained if we consider adding the on-site defect in the last resonatorbN.

Compared with adding a defect ona1orbNin the lattice,we find different interesting phenomenon when the large onsite defect potentials are added on the two ends of the lattice.In this circumstance,the system Hamiltonian manifests as

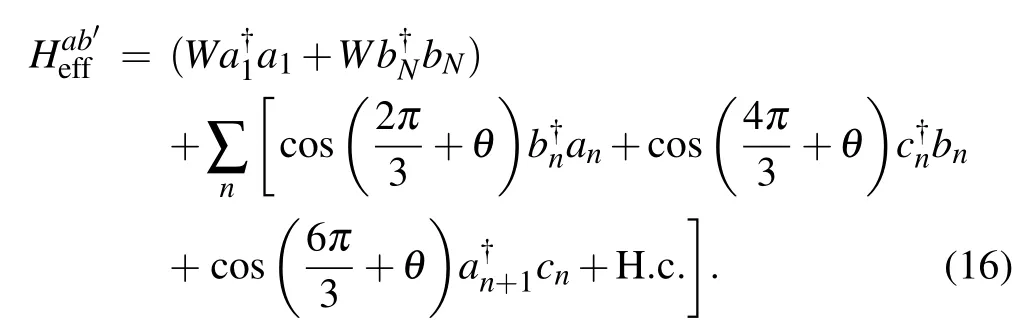
Here, we takeW=10.When the on-site defects are added ona1andbN, the two end resonators decouple from the initial lattice and the changed energy spectrum is shown in Fig.9(a), in which the different gap states are drawn in different colors.The state distributions and the corresponding time-dependent evolution of the green and red gap states are shown in Figs.9(b) and 9(c).Those of the blue and pink gap states are shown in Figs.9(d) and 9(e).From Fig.9(b), we can observe that the edge states mainly localize nearcN−1andaNat θ ∈(0,0.3π)∪(π,1.3π) while they appear nearb1andc1at θ ∈(0.3π,0.6π)∪(1.3π,1.6π).It means that a new two-qubit state transfer from the initial state| 0, 0, 0, ...,to the final state| 0, ..., 0, 0, 0〉 can be realized.The corresponding process of the state transfer between the new leftand the new right-edge states governed by Eq.(16)is shown in Fig.9(c).More interestingly, from Fig.9(d), we can observe that the distribution of the edge state only occupies a separate resonatoraNorb1.The edge state is concentrated on the second resonatorb1when θ =0.17π and θ =1.2π while it is localized in the penultimate resonatoraNat θ =0.5π and θ =1.5π.This is different form the case in any of the previous discussions, then it is natural to construct a channel of the single state transfer between the topological new left-and right-edge states.The corresponding evolution of the quantum state from the initial state|0, 0, ..., 0, 0, 0〉to the final state|0, 0, 0, ..., 0,is shown in Fig.9(e).

It should be pointed out that a previous research[46]has studied the influence of defects on QST with a superconducting qubit chain.In that work, the QST only occurs along thea-type resonators, so the on-site defects are added on theatype resonators(the first one and the last one)accordingly.Via designing the on-site defect added on thea-type resonators,a controllable switch mechanism of the QST channel is developed.Different from the former,we here study the on-site defect added on a singlei-type resonator(i=a,b,c)respectively or different types of resonators simultaneously, to systematically study the influence of the on-site defect on the edge states and QST.And the results here prove that the temperate on-site defects on suitable resonators can change the energy structure and state distribution of the circuit-QED lattice system.These changes drive the conversion of the current system from the two-qubits QST channel to a single-qubit channel.This novel controlling mechanism allows researchers to establish multifunctional QST channels without increasing or decreasing the size of the system.

Fig.9.The effect of the on-site defect added on the two ends of the resonators on the system.Here, we take g j (j=1,2,3,a,b,c) as the energy unit.(a) Energy spectrum with W =10.(b), (c) The distribution of the green(red)gap state and the corresponding time-dependent evolution of the initial state .(d),(e) The distribution of the blue (pink) gap state and the corresponding time-dependent evolution of the initial state 0, 0, ..., 0, 0, 0〉.Other parameters take N=7 and Ω =0.00001 in(c)and(e).

5.Discussion

Before concluding,a feasibility analysis for the schemes involved is necessary.First, the imperfection of experiment equipment and operations may causeJk=cos(+θ)(k=1,2, 3)to not be satisfied precisely.Under this circumstance, it is essential to study the influence of non-ideal coupling parametersJn−ideal=Vδ +cos(+θ) (k= 1, 2, 3) on our QST schemes, where δ is a random number in the range of[−0.5,0.5].Taking the two-qubit QST scheme in Section 3 as an example,we plot the energy spectrum corresponding to the imperfection coupling parameter withV=0.03 for the system in Fig.10(a).Note that some slight fluctuations appear in the band structure and the edge states produce tiny oscillations between the energy gap.In Fig.10(b), whenV=0.09,there are two gap states in the the energy spectrum and the edge states produce greater oscillations.However, when the disorder strength exceeds the size of the energy gap,the bulk structure will be broadened and the edge state will blend into the bulk state as shown in Fig.10(c).It is well known that larger perturbations of edge state will directly affect the effectiveness of QST.So, in Fig.10(d), we show the fidelity of QST vs.the non-ideal coupling strengthV.By the curve,we demonstrate that small fluctuations of coupling strengthVwill not greatly affect the performance of the scheme.

Fig.10.The effect of non-ideal coupling on the system.Here,we take gj (j =1,2,3,a,b,c) as the energy unit.(a) The energy spectrum of the system with V =0.03.(b)The energy spectrum of the system with V =0.09.(c)The energy spectrum of the system with V =1.13.(d)The fidelity of QST vs.the non-ideal coupling strength V and Ω =0.0005.The unit cells N=7.

Considering a closed Hilbert space, we can realize robust protocols of single-qubit and two-qubit QST theoretically.But,in the actual physical process,the influence of qubits decay and photon leakage out of the transmission line resonators should be considered.The conditional Hamiltonian of an open system for our physical model can be written as[56,57]

whereis given by Eq.(9).The second and the third terms represent the photon leakage out of the transmission line resonators and the decay of qubits, respectively.In our protocol, the role of superconducting qubit is to regulate the coupling strength between adjacent resonators, and the generalized SSH model mainly contains the coupling between two nearest-neighbor resonators.So, the photon leakage out of the transmission line resonators is the primary dissipative factor.The qubit spontaneous decay directly affects the coupling strength between adjacent resonators.It may causeJk=(k=1,2,3)to not be satisfied precisely.In Fig.10,we have already discussed the effect of imperfections on QST.Based on these analyses,we here consider the terms ofandfor an open system.Then,the system Hamiltonian can be written as

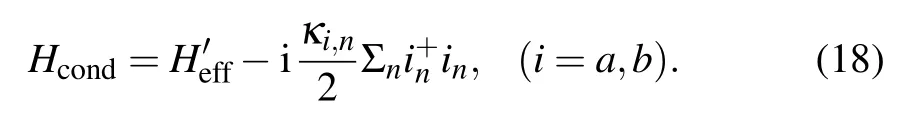
Because the edge states occupya-andb-superconducting resonators, we mainly consider the decay of these two kinds of resonators during the two-qubits QST.For convenience, we takeN= 3 as an example and assume κi,n=κ.The fidelity is formulated asF=〈R|ρ|R〉, where |R〉=|0,0,0,0,0,0〉(|10〉+|01〉)a3b3is the aim state of an ideal system, and the ρ is the final state governed by the conditional HamiltonianHcond.Figure 11 shows the relationship between the fidelityFand the different decay rate of resonators.As the decay rate of the resonators increases, the fidelities of the open system show a trend of decline.When the parameter Ω is Ω =0.003, the current QST channel can efficiently transfer the two-qubits state with 0.99 fidelity under considering the decay of the resonators.For Ω =0.001, the QST fidelity keeps 0.99 for κ/g∈(0.01,0.03).However, when κ/g∈(0.03,0.05),the fidelity decreases rapidly compared to the other two lines.The reason is that the appropriate adiabatic parameter Ω ensuring the current scheme is protected by the topological gap,but smaller adiabatic parameter means longer evolution time, which leads to a decrease in the effectiveness of the QST scheme in an open system with larger dissipation.Therefore, in an open system, the reasonable choice of adiabatic parameter Ω is helpful to improve the fidelity of the QST scheme.

Fig.11.The fidelity of the QST of|L〉→|R〉under the different decay rate κ of resonators when N =3.Here, we take gj (j=1,2,3,a,b,c)as the energy unit.

In addition,taking the characteristic of the adiabatic passage,we estimate the QST time of single-qubit(T1)and twoqubit states (T2).For the sake of discussion, we set the coupling strengthgj(j=1,2,3,a,b,c)between the TRL and the flux qubit to 1 as the energy unit.ForN=7 and Ω =0.00001,with the strong coupling strengthgj,n/2π =636 MHz,[53]the operation times ofT1= (0.5π −0.17π)/Ω ≈25.9 µs andT2=(0.5π −0.16π)/Ω ≈26.2 µs are both less than the decoherence time of a superconducting coplanar-transmissionline resonator.The lifetime of single microwave photon in superconducting coplanar-transmission-line resonator can reach 0.1 ms.[54,55]Therefore, our schemes can utilize the circuit-QED system such as coplanar resonators and qubits to realize under the development of the current technology,or in the near future.Moreover, the large couplinggiwith the conditiongi/Δi≪1 is realizable under current experimental conditions.Generally, the typical qubit level can be modulated in the range of 100 MHz to 15 GHz, providing a considerable adjustability in experiment.Forg/2π ≈600 MHz, the ratio ofgi/Δican be achieved at the highest 600 MHz/15 GHz≈0.04.In addition, we might be able to take advantage of the rapid development of fast QST methods, such as introducing the next-to-nearest-neighbor interactions of lattices to cancel nonadiabatic excitations[58]or constructing an exponential time-driving function to vary interchain couplings.[59,60]These methods can satisfy the adiabatic conditions under the premise of shorter time of QST.Therefore,it is of great potential to use accelerated adiabatic process in our model for reducing the coupling strength requirements and improving the feasibility of our schemes.

6.Conclusion

We have realized robust QST schemes based on a 1D circuit-QED lattice.After mapping the system into a generalized SSH model, the QST between the two leftmost resonators and the two rightmost resonators can be realized.We also investigate the influence of the on-site defect added on specific resonators on the QST.Remarkably, a change-over switch mechanism of the QST channel is developed via designing the on-site defect added on the first and the last resonators.In other word,when the on-site defects are added on the two ends of this lattice,a single-qubit state transfer channel is generated.Our work opens up a new way for the realization of topological quantum information processing and provides a path toward the different types of QST via adding the on-site defect on the resonator.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos.61801280, 61805134, and 61822114), the Applied Fundamental Research Projects of Shanxi Province,China(Grant No.201801D221015),and Science and Technology Innovation Project of Shanxi Normal University(Grant No.2020XSY032).

Appendix A:The time-evolve of a 8-resonator lattice chain

The Hamiltonian given in Eq.(9)is described as

whereJ1=cos(+θ),J2=cos(+θ)andJ3=cos(+θ).As a result,we obtain the Schrdinger equation as

According to this equation,first of all,we establish a system of differential equations based on the generalized SSH model.Then,for the initial state

we choose the appropriate adiabatic evolution parameter Ω,and the state of the system can be evolved from the time-dependent Schrdinger equation with

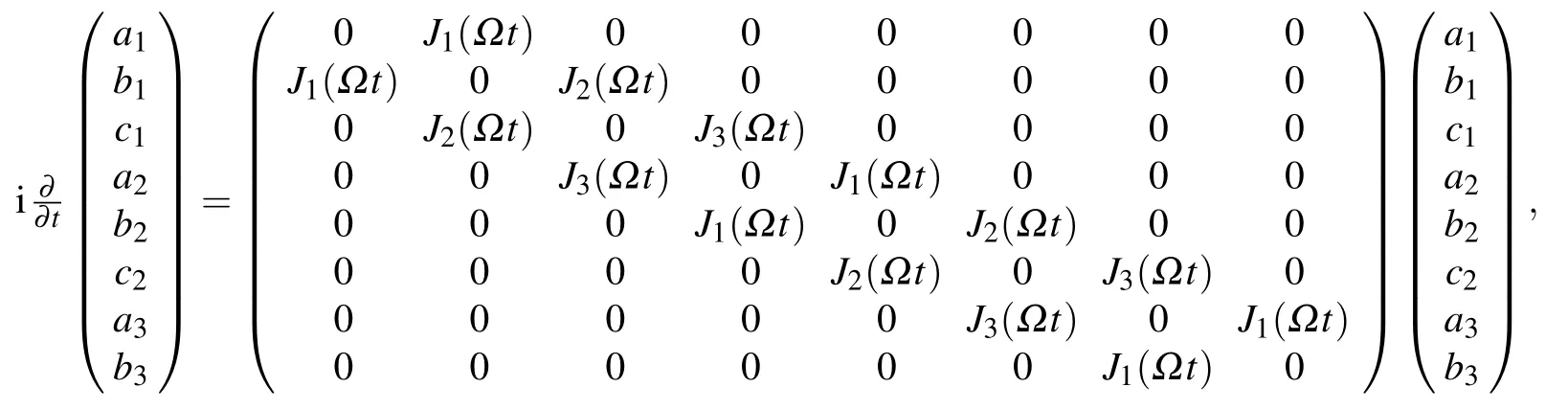
whereJ1(Ωt)=cos(+Ωt),J2(Ωt)=cos(+Ωt) andJ3(Ωt)=cos(+Ωt).

More specifically, from Figs.2 and 4, we can get that the edge state is localized in the two leftmost resonators when θ =π/6 or θ =7π/6, and in the two rightmost resonators when θ =π/2 or θ =3π/2.Here, we only demonstrate a single direction of evolution when θ ∈(0,π/2).In the range of θ ∈(0,π/2),the edge state is localized in the two leftmost(rightmost)resonators when θ =π/6(θ =π/2)).Therefore,according to θ =Ωt,the initial time and end time can be expressed astinitial=andtend=.Substituting the relevant parameters of Ω =0.0001,|L〉,tinitial=andtend=into the time-dependent Schrdinger equation,we can get the evolution of |L〉 as shown in Fig.4.The evolution of all size lattices withNis consistent with this process.