一种沉井潜入式竖井掘进机结构设计与研究

徐光亿， 肖 威， 赵 飞， 齐志冲， 吕 旦， 赵子辉

(中铁工程装备集团有限公司， 河南 郑州 450016)

0 引言

城市地下空间的开发利用已成为当今世界发展的趋势，并成为衡量城市现代化的重要标志。随着城市化的快速发展，城市可用面积越来越少。因此，开发和利用地下空间资源，修建与城市发展相适应的地下停车场、市政给排水管网、地下仓储等基础设施，对城市的建设与发展具有重要意义[1]。因此对应的施工装备——竖井掘进机应运而生。

在竖井掘进机的发展过程中，已有学者对其施工工艺、掘进装备未来发展、设备研究等方面进行了探索研究。刘志强等[2]对千米级竖井全断面科学钻进装备与关键技术进行了分析与研究。贾连辉等[3]提出全断面竖井掘进机上排渣技术，并对其关键技术进行了研究与试验。王鹏越[4]和杨仁树等[5]结合立井凿井技术及施工装备的历史发展，对竖井掘进装备的发展进行了探讨。刘志强[6]和荆国业等[7]分别介绍了利用导孔排渣的机械破岩竖井掘进机凿井工艺，并对掘进装备进行了论述。现有的研究多集中在设备的施工工艺、未来发展等方面，而关于设备本身的研究相对较少。

本文基于工业试验研发了一种新型竖井装备——沉井潜入式竖井掘进机，介绍了设备的应用工况、结构组成与工作原理；分析了设备工作装置受力特性，并对其进行了运动学分析；基于有限元分析方法和虚拟样机技术，对关键结构件进行了强度分析和动态仿真模拟。

1 依托试验项目

本项目依托于厂内工业试验模拟现场工况。为更真实的模拟竖井掘进机的工况，建立了试验台进行开挖试验。试验项目可以模拟真实现场竖井施工情况。试验采用基坑(井)内组装始发，为减小竖井深度，降低竖井建造难度，竖井试验台设计为地面始发，利用组装工装作为设备始发钢结构，进行设备始发掘进。基坑尺寸为上部直径7.95 m，深6 m，可以供掘进机进行开挖试验。图1为试验基坑(井)和设备始发现场照片。

样机工业性试验开挖介质为C30混凝土，开挖深度为0.5 m，试验切削效率约为30 m3/h。采用抓斗形式出渣，出渣效率约为40 m3/h。该竖井掘进机较好地完成了工业试验，成井精度控制在1‰以内，达到了预期效果。

(a) 试验基坑(井)

(b) 试验整机组装

2 结构组成及工作原理

沉井潜入式竖井掘进机是结合沉井工法的一种新型竖井掘进机，主要应用于城市给排水竖井设施建设，地下停车场、仓储设施建设，盾构始发井建设等领域，该设备是具有高安全性、集成化、机械化等特点的一种新型竖井施工设备。

沉井潜入式竖井掘进机由动力系统、开挖系统、推进系统、出渣系统、管片拼装系统、控制系统、纠偏系统等组成。主机结构主要由支撑装置、驱动装置、回转装置、伸缩油缸、工作臂、截割臂、截割滚筒等组成。

动力系统包括2部分： 1)由马达提供开挖装置的回转运动； 2)由截割臂上的电机提供截割滚筒旋转运动。

开挖系统创新性采用纵轴结构的截割滚筒设计，主要由截割破岩(土)滚筒、截割电机及其他辅助零部件等组成，工作原理是截割电机驱动截割滚筒旋转进行截割破岩工作。

其开挖轨迹从以下方面进行分析。

1)沿掘进方向的开挖轨迹分析。在截割滚筒开挖的过程中分为截割运动和进给运动，分别如图2和图3所示。其截割滚筒绕自身轴旋转的同时也在沿截割臂轴线方向推进，因此截割滚筒的运动轨迹为圆弧螺旋线，如图4所示。

v为速度； n为转速。下同。

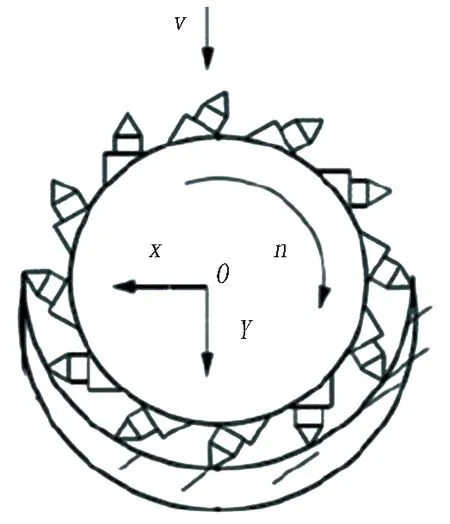
图3 进给运动示意图

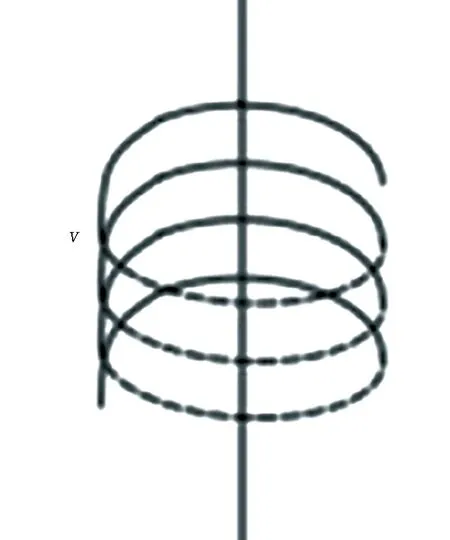
图4 圆弧螺旋线轨迹示意图

2)沿圆周摆动方向的开挖轨迹分析。当沿圆周方向摆动时，同时伴随着截割滚筒自身的旋转，因此截割滚筒的运动轨迹为沿圆周方向的圆弧螺旋线，图5为其中一段的圆周方向轨迹示意图。

3)最终形成的开挖轮廓。通过截割滚筒自身的旋转并通过伸缩油缸将其移动到某一基准位置进行定位，以定位基准位置依次向外进行回转开挖，达到所需的开挖轮廓。以开挖直径8 m为例，主机旋转共7圈，主机旋转依次向外进行开挖形成，开挖轮廓如图6所示。

ω为角速度。

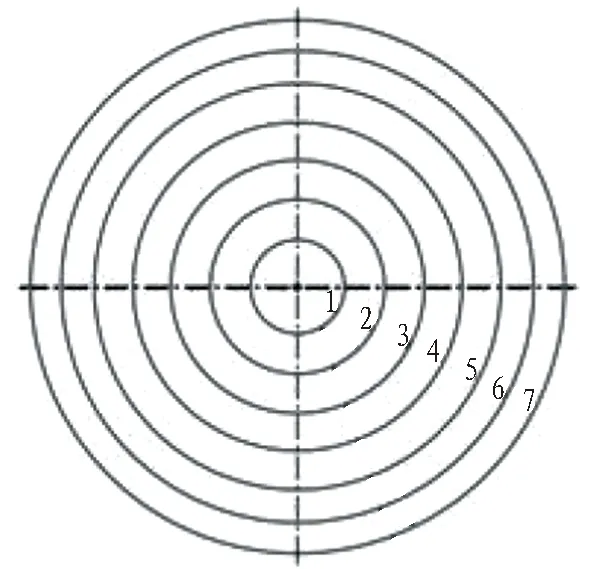
图6 主机旋转形成的开挖轮廓

推进系统基于滑箱轨道移动运动形式设计理念，创新性采用支腿与滑道形式来实现上下行程的移动。向下推进依靠推进油缸的伸出和预制管片的下沉来保证。

出渣系统可根据不同的地质条件采用不同的出渣方式。针对无水、少水地层，设备采用抓斗出渣的方式；针对富含地下水的工程采用泥浆出渣。

管节拼装系统由龙门架、管节吊机、吊机轨道等组成；控制系统由液压控制系统和电气控制系统组成，利用其控制系统融合动态感知模拟技术来实现实时监测与控制；纠偏导向系统由纠偏导向仪和加压装置两者协同进行控制。主机主要结构组成示意如图7所示。

该沉井潜入式竖井掘进机结构小巧灵活，对地层及地面环境的扰动小，竖井断面尺寸和形状可变，远程控制和操作，模块化设计可根据需求进行灵活选配和定制。

3 掘进机的力学特性分析

沉井潜入式竖井掘进机在掘进过程中会伴随着预制管片或现浇结构管片的拼装来支撑井壁，设备的土压力靠管片来承受，因此在计算掘进机的受力时，无需考虑来自井壁土压力的作用，只需计算设备掘进过程中的受力即可。

在设备开挖过程中，工作装置产生轴向进给力F轴向力、圆周回转力F周向力、自身重力G1。设备受力示意如图8所示，主要受到的力(考虑开挖位置在极限位置处)为截割滚筒压力所产生的反力矩、截割滚筒轴向进给力引起的倾覆力矩[8]。

图7 主机主要结构组成示意图

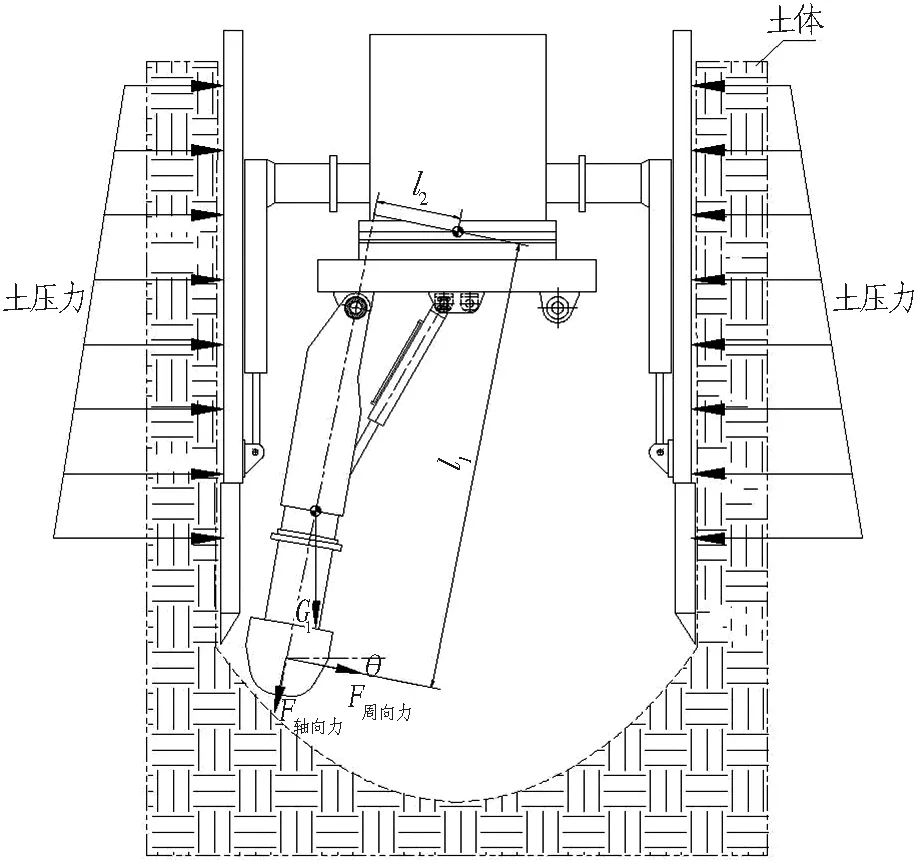
图8 设备受力示意图

截割滚筒压力所产生的反力矩(逆时针方向)

M1=F周向力×l。

(1)

截割滚筒轴向进给力引起的倾覆力矩

M2=F轴向力×l。

(2)

中部回转装置受到的轴向力

F1=G1+F周向力×sinθ。

(3)

式(1)—(3)中：M1为截割滚筒压力所产生的反力矩；M2为截割滚筒轴向进给力引起的倾覆力矩；G1为设备自身重力；F1为回转支承受到的轴向力；θ为F周向力与水平方向的夹角；L为开挖装置与设备重心位置的直线距离。

4 工作装置的运动学模型构建与分析

根据掘进机实际工作过程中工作装置的运动状态，建立其工作装置的运动简化模型，如图9所示。 伸缩油缸活塞杆的伸出和收回会引起工作臂空间转角的变化。OA为固定臂，OB为转动臂，BC为截割头部，v1为油缸伸缩的速度方向，v2为设备掘进速度方向。

θ为转动臂OB与固定臂OA的夹角，(°)； α为转动臂OB与前进速度的夹角，(°)； a为固定臂OA的长度，mm； b为转动臂OB的长度，mm； l为液压缸伸出的长度，mm; 下同。

由图9，可得：

(4)

θmin=αmin+β(β=90°) 。

(5)

(6)

(7)

(8)

以O点竖直向下位置为界线，以当前位置OB转动臂依靠油缸收缩向中间竖直位置摆动的工况可得：

(9)

以O点竖直向下位置为界线，以当前位置OB转动臂依靠油缸收缩从中间竖直位置向右侧摆动的工况可得：

(10)

以截割臂为研究对象，通过截割臂中心点的位置坐标[x,y]以及截割臂的姿态角α可以确定截割臂的空间状态，用矢量[xyα]T表示。

1)以当前OB截割臂的活动范围在X轴竖直位置的左侧范围摆动的工况1进行分析。

在设备掘进的过程中，为了便于研究，假设液压缸活塞杆直线往复运动速度和下沉掘进速度是恒定的，分别为v1和v2。将大地视为定坐标系XOY，将该机构视为动坐标系(以转动点O为坐标原点，掘进方向为X轴，与掘进方向垂直的方向为Y轴)，如图10所示。

图10 运动工况1空间姿态简图

截割臂参考点的位移矢量为EE1，参考点位置E1坐标可以表示为：

(11)

式中：h1表示掘进机向下掘进的深度，mm；c表示截割滚筒参考点E到转动点O的距离，mm；θ1表示该空间任意状态下工作臂OB与固定臂OA的夹角。

截割臂在伸缩油缸伸出阶段的姿态空间状态可以表示为：

EE1[]T=[x1y1α1]T

=[h1+c·sinθ1-c·cosθ1θ1-β]T。

(12)

同理，截割臂在油缸伸出阶段状态的基础上继续向下掘进深度h2，油缸保持状态下的姿态空间状态可以表示为：

E1E2[]T=[x2y2α2]T

=[h1+h2+c·sinθ2-c·cosθ2θ2-β]T。

(13)

同理，截割臂在油缸保持状态下的基础上继续向下掘进深度h3，油缸收回状态下的姿态空间状态可以表示为：

E2E3[]T=[x3y3α3]T

=[h1+h2+h3+c·sinθ3-c·cosθ3θ3-β]T。

(14)

2)以当前OB截割臂在X轴正中竖直位置向下掘进的工况2进行分析，如图11所示。

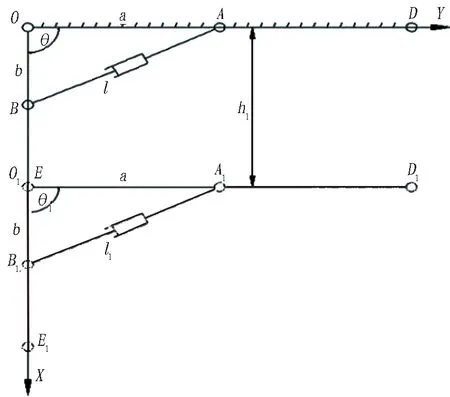
图11 运动工况2空间姿态简图

截割臂姿态空间状态可以表示为：

EE1[]T=[x1y1α1]T=[h1+c0β]T。

(15)

3)以当前OB截割臂的活动范围在X轴竖直位置的右侧范围摆动的工况3进行分析，如图12所示。

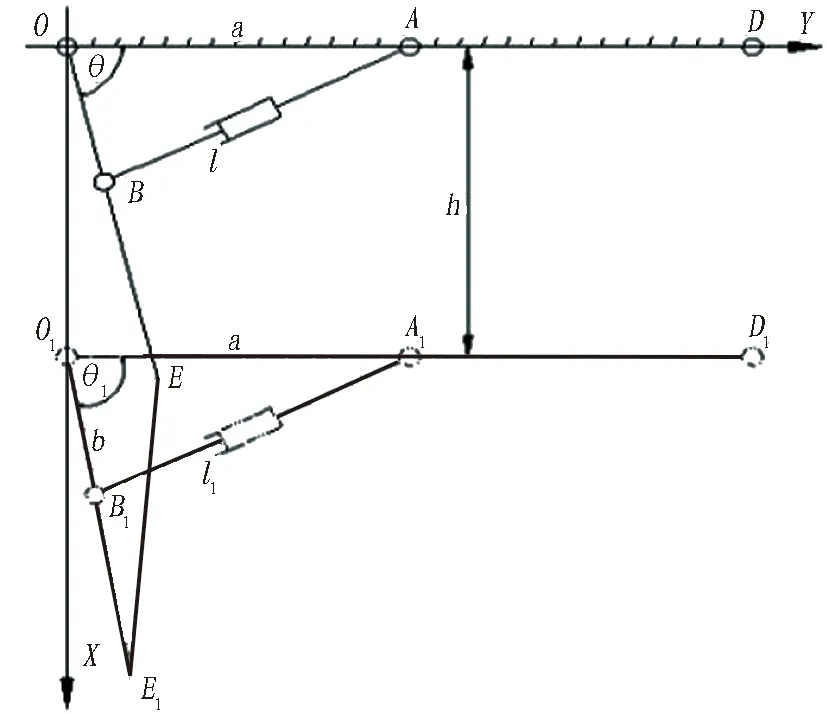
图12 运动工况3空间姿态简图

(16)

截割臂在油缸伸出阶段的姿态空间状态可以表示为：

EE1[]T=[x1y1α1]T=[h1+c·sinθ1c·cosθ1β-θ1]T。

(17)

同理，截割臂在油缸伸出阶段状态的基础上继续向下掘进深度h2，油缸保持状态下的姿态空间状态可以表示为：

E1E2[]T=[x2y2α2]T

=[h1+h2+c·sinθ2c·cosθ2β-θ2]T。

(18)

同理，截割臂在油缸保持状态下的基础上继续向下掘进深度h3，截割臂在油缸收回状态下的姿态空间状态可以表示为：

E2E3[]T=[x3y3α3]T

=[h1+h2+h3+c·sinθ3c·cosθ3β-θ3]T。

(19)

5 设备关键部件的有限元分析

5.1 工作臂有限元分析

工作臂作为整机主要的运动与支撑零部件，是连接回转运动以及截割滚筒的关键结构，在实际工作过程中工作臂的受力情况对于整机的可靠性至关重要，因此需要对其进行强度分析。

5.1.1 有限元模型的建立

在不影响精度的前提下，建立计算模型时，应简化模型结构，以提高运算速度。为此，对模型进行几何修改，将模型上的非倒角结构和圆角以直角代替，然后进行网格划分[9-10]。采用有限元法对工作臂三维模型进行网格划分，如图13所示。采用四面体网格，划分网格单元数量95 594，节点数量177 080。采用四面体结构单元和线弹性材料模型，在网格划分前先赋予结构材料属性，定义材料的弹性模量为206×103MPa，泊松比为0.3。

5.1.2 材料的设置与参数

结构采用Q345B焊接而成，其材料参数见表1。

5.1.3 载荷与边界条件

根据受力情况，在上部连接位置处与侧部伸缩油缸连接固定位置处施加固定约束，与下部截割臂连接端面的位置施加600 kN·m的力矩，并添加重力约束。工作臂施加边界条件如图14所示。

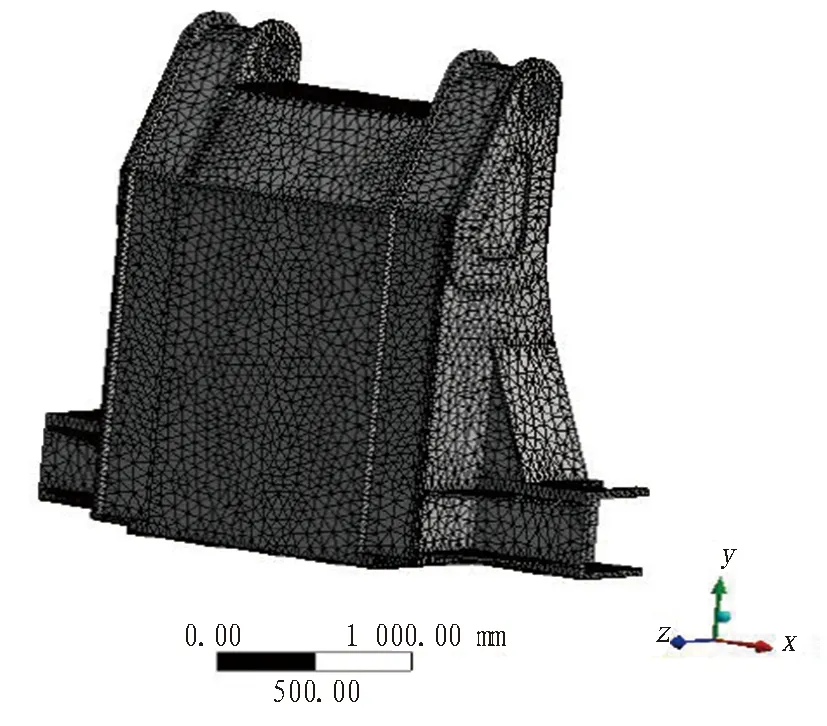
图13 工作臂三维模型网格划分

表1 材料参数表

图14 工作臂边界条件

5.1.4 应力分析

图15为工作臂应力云图。从图15分析结果可知，工作臂大部分区域的应力在150 MPa以下，局部会由于三维模型绘制的结构尖角以及尖角过渡处出现应力集中导致应力值变大。在由于计算简化引起的应力值变大的位置，可以采用较大直径圆角过渡处理，这样可大大降低这些位置的应力值[9]。因此工作臂结构整体受力状况较好，满足设计要求。

图15 工作臂应力云图(单位： MPa)

5.2 回转装置有限元分析

回转装置是回转运动的关键结构件，回转装置是连接驱动装置与开挖装置的载体，其受力情况相对较差，因此需要对其进行强度分析。

5.2.1 有限元模型的建立

网格划分如图16所示，采用四面体网格，划分网格单元数量95 594，节点数量177 080。采用四面体结构单元和线弹性材料模型，在网格划分前先赋予结构材料属性，定义材料的弹性模量为206×103MPa，泊松比为0.3。

图16 回转装置三维模型网格划分

5.2.2 载荷与边界条件

回转装置约束与加载情况如图17所示。在上部法兰连接端面位置处做固定约束处理；在底部端面及圆周面处施加回转力矩和倾覆力矩；施加斜向力；添加重力。

图17 回转装置约束与加载情况

5.2.3 应力分析

图18为回转装置应力云图。从图18分析结果可知： 回转装置的应力在110 MPa以下，结构的整体受力状况较好，满足设计要求。

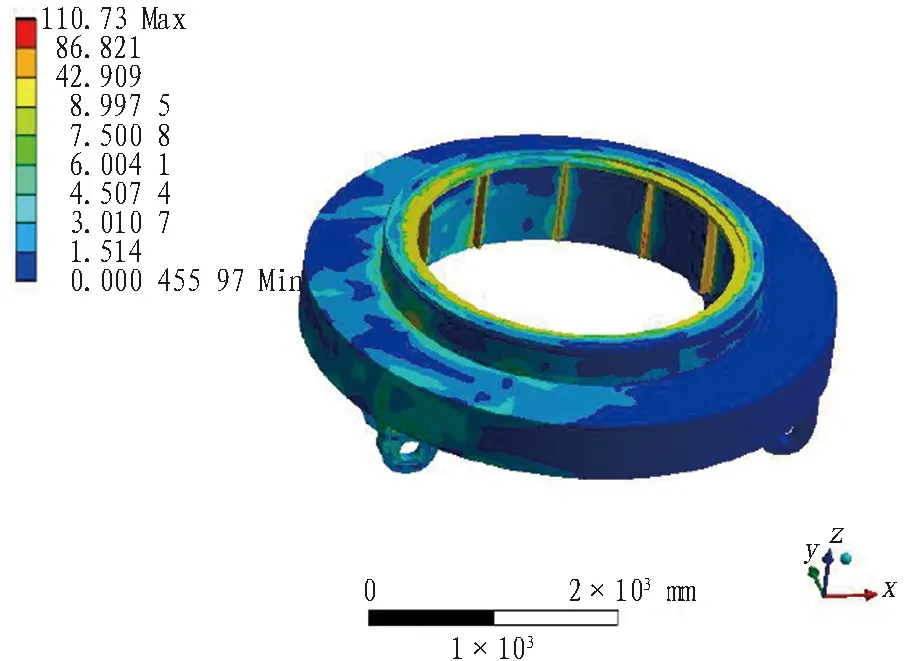
图18 回转装置应力云图(单位： MPa)

6 工作装置运动学及动力学分析

对工作装置进行三维建模并简化，然后把模型导入仿真软件中建立虚拟样机模型，并进行模型定义与各种约束、驱动和力的添加，具体包括以下部件的定义： 2个球铰副、5个旋转副、2个移动副、5个固定副、1 个齿轮副、2个液压缸驱动、1个回转驱动和1个结构重力[11-13]。

工作装置的运动形式有2种： 1)上部驱动带动回转装置进行工作装置的回转运动； 2)伸缩油缸的伸缩带动工作臂及截割滚筒的摆动运动。

6.1 回转运动

以回转装置旋转为主，设置时间为35 s，设其驱动函数为：

STEP(time,0, 0, 5, 190 d)+STEP(time, 5, 0, 15, -190 d)+STEP(time, 15, 0, 25, -190 d)+STEP(time, 25, 0, 35, 190 d)，根据函数设置进行仿真分析。

回转运动与工作臂质心运动曲线如图19所示。可以看出在0～5 s其速度曲线波动较大，其余时间运动相对平稳。整个位移曲线呈现规律性的变化，符合实际运动情况。

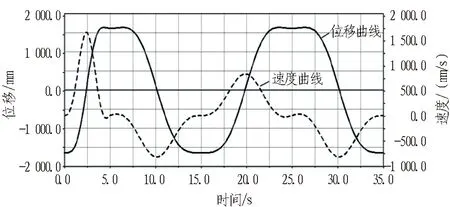
图19 回转运动与工作臂质心运动曲线

工作臂与回转装置连接处的受力曲线如图20所示，可以看出其受力曲线呈现规律性变化，0～15 s为1个周期循环变化，其受力最大值为300 kN。

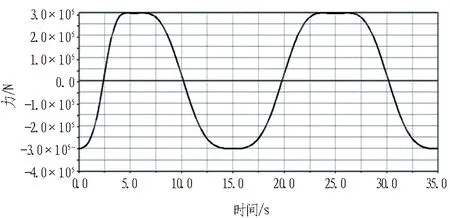
图20 工作臂与回转装置连接处受力曲线

6.2 摆动运动

以伸缩油缸伸缩为主，设置时间为80 s，设其驱动函数为：

STEP(time, 0, 0, 10, 500)+STEP(time, 10, 0, 20, -500)+STEP(time, 20, 0, 30, -500)+STEP(time,30,0,40, 500)

摆动运动与工作臂质心运动曲线如图21所示，可以看出其位移曲线随着油缸的伸缩运动呈现规律性变化；其速度曲线在油缸伸出与收缩的转换点出现尖峰，其余时间速度相对平稳。

工作臂与回转装置连接处的受力曲线如图22所示，可以看出其受力曲线呈现规律性变化，最大值为580 kN，最小值为220 kN。

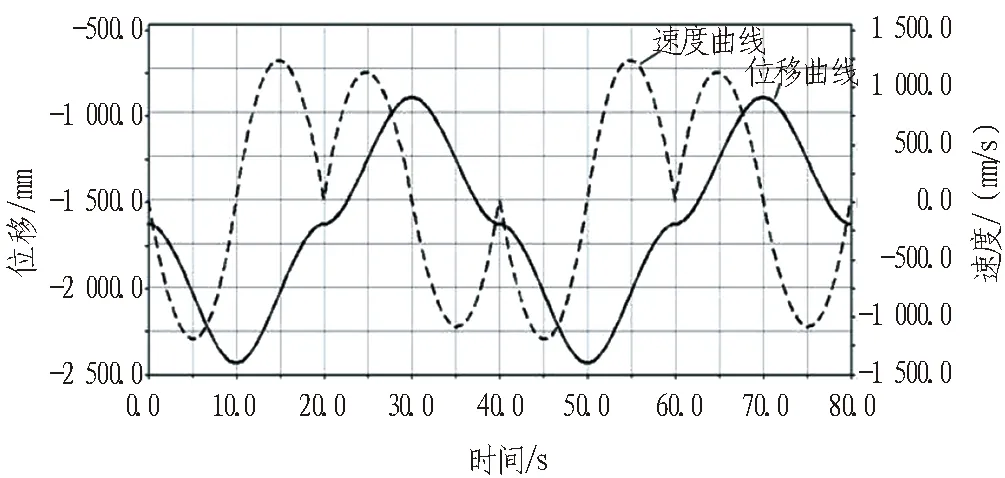
图21 摆动运动与工作臂质心运动曲线

图22 工作臂与回转装置连接处受力曲线

7 结论与讨论

本文建立了沉井潜入式竖井掘进机的力学模型，基于力学模型对掘进机的回转装置、工作臂进行静强度分析，验证了其在强度和刚度方面设计的合理性。以工作装置为研究对象，基于运动学模型对工作装置进行了运动学理论分析。基于虚拟样机技术，在回转运动和摆动运动2种运动形式下，对其工作臂以及连接位置处进行了运动学研究和动力学研究。

在设备掘进过程中，整机的自动化作业可大大提高施工效率，整机的轻量化设计、安装与吊装作业的方便快捷也可大大提高作业效率，从而降低设备制造以及施工成本。因此，整机零部件的轻量化设计研究以及结构设计的自动化程度可作为接下来的探索方向。