基于信息熵的商业银行客户画像属性约简研究

张宇敬,王柳,齐晓娜,许美玲,王蕾

(河北金融学院 信息工程与计算机学院，河北 保定 071000)

随着大数据、云计算和人工智能等技术的不断发展以及中国投资顾客群结构的变化，如何通过新技术、新工具设计个性化的资产管理服务是商业银行等资产管理行业在未来的市场竞争中致胜的重要一环.智能投顾作为人工智能在财富管理领域的重要应用，近年来受到广泛关注.智能投顾的概念于2002年首次被提出，将传统上由人工提供的理财顾问服务转变为使用具有人工智能的计算机程序系统，它可以根据客户自身的理财需求，通过一系列的算法和产品搭建起数据模型[1]，其先进性在于能够针对投资者的不同风险偏好、预期收益，对其进行资产画像并形成个性化的资产配置方案，提供差异化服务.

智能投顾的基础在于提升数据挖掘能力，对投资者进行精准画像.商业银行有客户的基本信息和许多交易运营数据，这些可靠的内部数据可以真实客观地反映客户的一些特性[2]，基于银行可靠的数据构建以业务需求为核心、具有实践应用意义的体系、清晰客观可读的客户画像，能够有效驱动精准营销.近年来，国内外学者针对客户画像提出了不同的聚类算法并取得了一定成果，但银行类数据维度较高，客户画像的数据维度并不是越多越好，面对高维的复杂的银行类客户数据，往往需要进行属性约简提取数据中重要的特征，并摒弃掉无用的特征.通过属性约简将模型从较多的维度空间通过空间映射变成较少的维度，可以改善变量间关系或减少计算量[3].目前，属性约简利用粗糙集、粒计算、形式概念分析和智能算法等方法进行,多种属性约简算法的融合研究是属性约简算法的发展趋势[4].张晨等[5]在研究多属性评价决策时引入信息熵的概念，并建立了中国的商业银行操作风险的多属性评价方法.王曼怡等[6]基于信息熵的中国的银行同业业务流动性风险研究，确定了外部经济环境、内部资源整合、社会融资需求和金融监管政策为4个主要考量因素.杜光辉等[7]将粗糙集理论应用到商业银行的整体风险评价研究中,对16家上市银行的实证研究，建立风险评估体系.文献[8-11]等分别将粗糙集与不同类别的信息熵相结合进行属性约简和特征选择，完成指标构建.基于粗糙集理论和信息熵进行银行数据的属性约简并不是很普遍.故而本文基于粗糙集理论和信息熵对构建客户画像模型的属性进行约简,从高维数据中有效筛选出关键属性，这对将客户信息进一步准确的数据化有重要意义.

1 使用聚类分析对客户画像

1.1 客户画像概述

客户画像本质是将客户的特征进行标签化，并收集与分析客户的属性信息，利用数学模型将客户信息进行归纳总结，形成“源于数据、高于数据”的客户标签[12]，客观真实地描绘客户.研究客户画像的目的在于能够以数据化思维方式思考，并用数据的手段帮助许多行业进行精准营销.除此之外，企业使用数据分析结果可以进一步优化用户体验，拓展商业模式.

客户是商业银行经营活动的基础，但银行客户相关信息较多且复杂，客户管理存在一定困难.将庞大的客户信息数据化，使用机器学习技术对客户数据深度分析，利用客户画像系统管理客户，将客户进行有效的细分，了解到不同客户的不同需求，能够调整发展战略，提高银行的工作效率，增加其在行业竞争力.

1.2 K-means聚类算法

对客户画像的研究中，使用较广泛的是聚类算法.聚类是数据挖掘中的一种主要技术手段，它的主要思想是把一组个体按照相似性归纳为若干类别，聚类的目的是使同一类中个体间的相似度高于其他类的对象[13].本文选择基于划分的聚类方法K-means聚类算法，该算法需要提前指定类簇数目即K值，然后通过不断循环迭代将数据进行分组，算法简单,适用性广,运算速度快，并且可以通过分析类簇中心点来观测各类簇数据的特点.以下为该算法的具体描述：

输入 数据集D，划分簇的数目K

输出K个簇的集合

1)随机初始化K个簇类中心

2)repeat

3) for 数据集中的每个对象i

5) end for

6) for 每个类簇j

8) end for

9)until 收敛

K-means算法首先选择初始类簇中心点，然后对于数据集中的每个样本计算其到类簇中心点的距离，并根据距离将样本划分到相应类簇，每轮迭代完成之后重新更新类簇中心点，直到收敛(如类簇中心点不再改变).该算法对初始类簇中心点的选择有较高的依赖性，并且容易求得局部最优解，因此，应该进行多次实验，取最优的聚类结果.

2 基于粗糙集理论及信息熵的属性约简

2.1 粗糙集的基本概念

波兰数学家Pawlak于1982年提出粗糙集理论[14]，它从上近似集和下近似集的角度描述系统的不确定性，是一种处理不精确及不确定性数据的数学方法.粗糙集在数据的决策、模式识别和机器学习等领域得到了广泛应用.下面简要介绍一下粗糙集理论的相关知识.

信息系统与决策表：信息系统即用来表示粗糙集理论所研究的对象的数据表(即属性-值表).

定义1[15]假设S=(U,A,V,f)为一个信息系统(知识表达系统)，其中

U是对象的非空有限集合，称为论域；

A是属性的非空有限集合，A=C∪D,C∩D=Ø,C为条件属性集，D为决策属性集，决策表是具有决策属性集和条件属性集的信息系统；

V=Uα∈AVα，Vα是属性a的值域；

f:U×A→V称为信息函数，它为对象的每一个属性都有一个相应的信息值.

对于每个属性子集B⊆A，定义不可辨的二元关系IND(B)={(x,y)∈U×U|∀r∈B,r(x)=r(y)}.当IND(B)为一个等价关系RB时，RB将论域划分为若干个等价类，记为U/RB={[X]B|x∈U}.简记为U/B.

上近似集与下近似集：在粗糙集理论中，任何一个不确定集都可以用下近似集和上近似集来逼近，2个集合的定义如下.

定义2[15]给定一个信息系统S=(U,A,V,f)，R是系统S上的一个等价关系，对于∀X⊆U，定义X的R的下近似集和R的上近似集分别为

R(X)=∪{Y∈U/R|Y⊆X}={X∈U|[X]R⊆X},

属性约简和核：属性约简既能保证决策表具有正确分类能力，也能去除不必要的信息[16].

定义3[15]给定一个信息系统S=(U,A,V,f)，A=C∪D.对∀α∈C，如果有

1)U/(C-{a})=U/C，则称a为不必要属性(冗余属性);

2)U/(C-{a})≠U/C，则称a为必要属性.

若P⊆C，如果满足：

1)U/P=U/C,

2)∀α∈P，U/(P-{A})≠U/C,

则称P是C的一个约简.

C中所有必要属性的集合称为C的核，记成core(C)[17].容易证明core(C)=∩red(C)，其中red(C)表示C的所有约简.核包含在所有的约简之中，可以作为所有约简的计算基础，并且作为知识最重要部分的集合，在约简过程中核是不能够忽略的.

2.2 基于信息熵的属性约简

信息熵是总体不确定性度量的一种方式，它是表示数据的统计特征[18-20].将粗糙集理论中的信息和知识建立关系，从信息熵的角度对属性进行约简，并最终获得高效的属性.

定义4设U是一个论域，P和Q为论域U上的2个等价关系族(即知识)，X、Y分别为P和Q在U上的划分，其中U/IND(P)={X1,X2,…,Xn}；U/IND(Q)={Y1,Y2,…,Ym}，则P、Q在U的子集上的概率分布定义如下：

定义5[15]属性集合P的熵为

定义6[15]属性集合P相对于属性集合Q的条件熵为

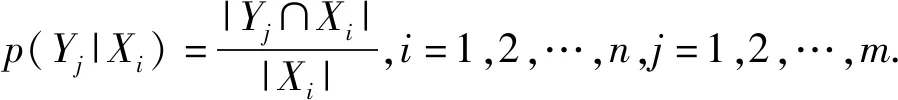
P和Q的互信息为

I(P,Q)=H(Q)-H(Q|P).

属性约简的目的在于找到对于决策结果影响更大、更重要的条件属性，必须考虑条件属性和决策属性两者的互信息.核作为知识最重要部分的集合，包含在所有相对简约之中，因此本文将核作为求属性约简的起点，在此基础之上逐步添加重要程度较大的属性，直到达到属性简约的终止条件.在这里，为了表达各个属性之间的重要程度，使用属性引起的互信息量的增量表示，定义属性的重要性如下：

定义7设T=(U,C∪D)为一个决策表，R⊂C且对于任意属性a∈C-R的重要性定义为

SGF(α,R,D)=H(D|R)-H(D|R∪{α}).

若R=Ø，则SGF(α,R,D)=H(D)-H(D|α)即为属性a与决策D的互信息.

SGF(α,R,D)的值越大，表示在已知属性的基础上增加属性a后，对决策结果的影响更大，即属性a对决策结果D更重要.

本文提出的属性约简算法描述如下.

输入 决策表T=U,C∪D，其中U为论域，C和D分别为条件属性集和决策属性集.

输出 条件属性集C的约简R.

Step1 计算条件属性集C相对于决策属性集D的核core=core(C).

Step2 计算C与D的互信息I(C,D).

Step3 令R=core，重复：

1)对每个属性a∈C-R，计算SGF(α,R,D).

2)选择使SGF(α,R,D)达到最大的属性a，若有许多属性可以同时使SGF(α,R,D)达到最大值，那么应该选择与R属性组合数最少的属性记作a，令R=R∪{α}.

3)若I(R,D)=I(C,D)，Step4；否则1).

Step4 输出R.

3 实验及结果

3.1 数据描述及预处理

本文的研究数据来源于某商业银行的真实客户数据，包括描述个人基本特征的人口属性(如性别、年龄、婚姻状况、子女数目)，描述客户收入情况及支付能力的信用属性(如受教育程度、职业、职务、工作单位性质、年收入、居住房屋类型、信用卡额度、累计逾期期数、月均存款、违约次数)，描述客户消费习惯及偏好的消费属性(车贷笔数、房贷笔数、个人常用流水6个月以内均值及标准差)，经过脱敏处理后特征总维度为69，样本数量4 521.

原始银行客户数据维度很高，模型训练难度及训练开销极大，且字符串类型数据过多，在建立模型之前首先对数据进行以下预处理操作.

1)数据归约：指在基本保持数据“原貌”的前提下，最大限度的化简数据集.首先进行维度规约，选取年龄(Age)、婚姻状况(Marital)、受教育程度(Education)、职业(Job)、违约情况(Default)、年收入(Year-income)、住房贷款情况(Housing)、个人贷款(Loan)情况等8个属性进行聚类.其次进行概念分层，将年龄分为少年、青年、中年、老年.

2)数据规范化：把属性值按比例缩放至特定区间，如[0,1].本文使用的数据集中，年收入最高90 000 000，最低为0，平均值为654 699，将平均值设为阈值，收入高于平均值的都设为3，低于平均值的转化到[0,3)内.

3)数据类型转换：将字符串类型的数据转换为数值型，方便K-means聚类距离计算.如婚姻状况，离异转换为0，单身转换为1，已婚转换为2.

各变量的处理情况如表1所示.

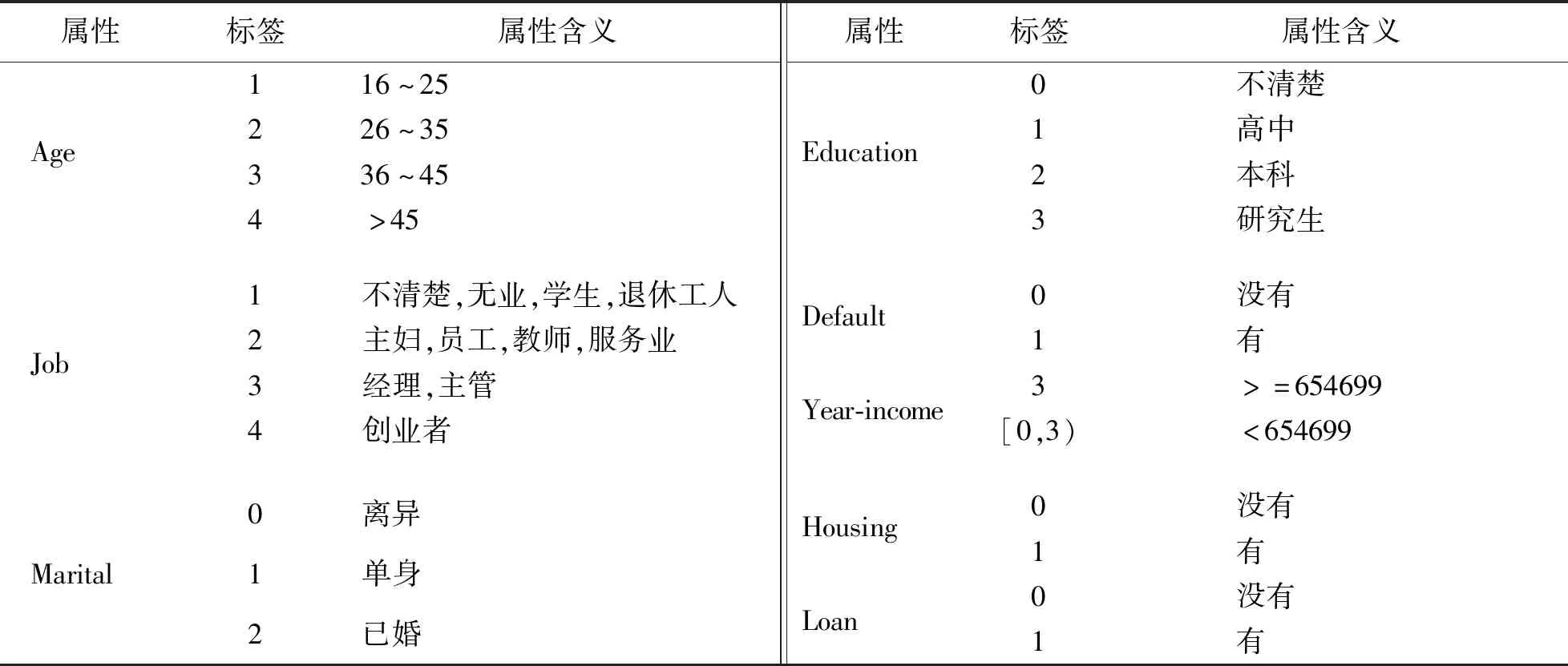
表1 各变量处理对照表Tab.1 List of each variable

3.2 K-means聚类结果

使用K-means算法将客户分为3类，图1选取部分样本点进行了展示(展示结果为principal component analysis即PCA降维之后的数据)，白色标记部分代表3个类别的类簇中心点.以下针对3类客户进行特征分析.

图1 聚类结果(PCA降维后的数据)Fig.1 Clustering results(Data after PCA dimension reduction)

第1类客户定义为潜力客户，其类簇中心点的特征如表2所示，该类型客户年龄在25岁左右，工作多为学生或职场新人，婚姻状况处于未婚单身状态，暂时还没有房贷压力，有个人贷款且年收入较少.该类型的客户现阶段对于银行的贡献比较小，但是该类型的客户发展空间较大，可针对其推荐风险较小的固定收益理财产品，该类型的客户在未来可逐渐上升优质客户.

第2类客户定义为一般价值客户，其类簇中心点的特征如表3所示，该类型的客户的年龄处于45岁左右，生活稳定收入中等的已婚人士，房贷和个人贷款压力较小，该类型的客户为银行的一般类型的客户，有一定的贡献值，但大多数偏向于保守型，更倾向于投资保守型、风险谨慎型的理财产品.应重点培养该类型客户的忠诚度，避免客户流失.

表2 第1类客户Tab.2 First class customers

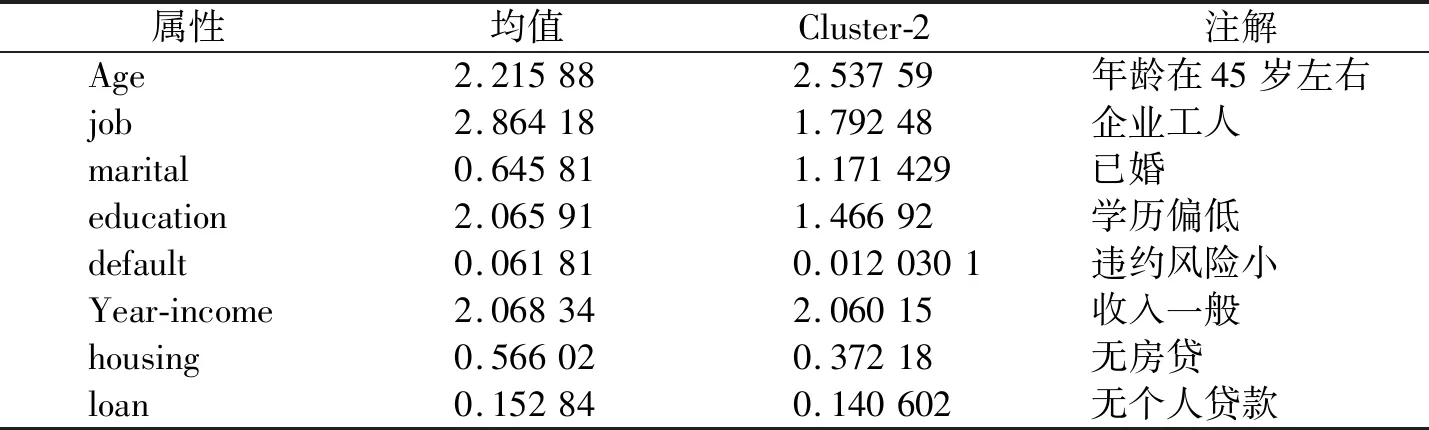
表3 第2类客户Tab.3 Second type of customers

第3类划分为优质类型客户，其类簇中心点的特征如表4所示，该类型的客户的年龄处于35岁左右，婚姻稳定，学历较高，事业处于上升期且收入较高，该类型的客户投资理财产品可能性较大，且风险承受能力和新事物的接受能力较强，对银行的贡献度较大，是银行重点关注的价值较高的客户.在理财产品的推荐方案中可适当推荐风险型较高、收益率较大类型的理财产品.

表4 第3类客户Tab.4 Third category of customers

3.3 属性约简

针对聚类之后的数据，确定年龄和职业为核属性，即R0={年龄，职业}，条件属性为C={年龄、婚姻状况、受教育程度、职业、违约情况、年收入、住房贷款情况、个人贷款情况}，决策属性为D={第1类客户，第2类客户，第3类客户}.按照本文提出的属性约简算法计算其他6个属性的重要性，以婚姻状况为例：

1)根据聚类结果第1类客户样本数1 886、第2类客户样本数1 305、第3类客户样本数1 330，根据定义5决策属性的信息熵为

2)根据定义6，决策属性相对于核属性的条件熵为

H(D|R0)=0.76.

3)根据定义6，决策属性相对于属性集合CU{婚姻状况}条件熵为

H(D|R0∪{婚姻状况})=0.11.

4)根据定义6，属性婚姻状况的重要性为

SGF(婚姻状况，R0,D)=H(D|R0)-H(D|R0∪{婚姻状况})=0.65.

依次计算其他属性的重要性，属性重要性计算结果如表5所示.

表5 属性重要性计算结果Tab.5 Significance of attribute

因为I(R0∪{婚姻状况，受教育程度}，D)=I(C,D)所以得出约简后的条件属性为年龄、职业、婚姻状况、受教育程度.

4 结语

目前，客户画像技术已成为各行业的研究热点，但商业银行客户数据维度较高，如何从高维数据中筛选出有效属性，对准确地进行客户画像分析有重要意义.本文提出了基于信息熵的属性约简算法，将其应用于真实的商业银行客户数据.首先根据条件信息熵约简选出年龄、婚姻状况、受教育程度、职业、违约情况、年收入、住房贷款情况、个人贷款这8个重要属性，然后对这8个属性进行聚类分析，根据聚类结果使用信息熵属性约简法对商业银行客户画像属性进行约简，得出年龄、职业、婚姻状况、受教育程度4个属性，实验结果表明本文提出的算法有效、可行.