基于多元回归模型的超市商品“薄利多销”有效性的实证研究*

金慧峰，王积建

（浙江工贸职业技术学院，浙江 温州 325035）

0 引言

“薄利多销”是指用低利低价卖出去商品来增加总收益的销售策略。在确保质量和价格优势的情况下，薄利多销能吸引更多客户，从而扩大销售规模，增加市场份额，迅速占领市场，同时能够促进企业扩大生产，加速资金周转速度，增加企业盈利。

只有需求富有弹性的商品才能“薄利多销”。实行薄利多销的商品，必须满足需求价格弹性大于1。[1]可见，在实际经营过程中，“薄利多销”不是普遍适用的法则，它有其特定的使用范围和使用条件，于是众多学者就薄利多销的必要条件进行了研究。徐贤浩、陈雯和沈古文（2011）提出只有当价格内生时，若策略消费者比例较大，薄利多销的天天平价策略能够吸引策略消费者尽早购买；[2]李春梅（2005）提出运用差量利润为零的销量价格平衡关系，为企业正确采用薄利多销提供指导；[3]冯长焕（2001）提出了在“区段价格折扣”条件下最优售价的确定方法，以及在薄利多销决策情况中若出现价降量增幅度不一致时降价促销方案是否可行的定量判定标准；[4]李春香（2006）提出薄利多销价格策略的条件包括：商品富有价格弹性、消费者具有与薄利多销相应的消费心理、竞争者之间避免价格大战、企业应达到的基本素质以及把握好薄利多销的最佳时机。[5]

总之，现有文献对薄利多销策略的必要条件进行了广泛而深入的研究，但缺乏针对商品大类或具体某种商品在薄利多销是否可行方面的实证研究。2019年全国大学生数学建模竞赛E题关注了这个问题，[6]本文以该赛题提供的某大型百货商场2016 年11月30日至2019年1月2日的销售记录为依据，研究打折力度与商品销售额以及利润率之间的关系，为商场制定营销策略提供决策参考。

1 超市商品“薄利多销”有效性的实证分析

以国内某大型超市商品2016 年11 月30 日至2019 年1 月2 日的销售记录为依据，数据信息比较庞大，其中销售记录表有超过100 万条的记录，因此需要使用数据库技术，把几个数据信息表建立关联，实现数据的查询、清洗和分析。

以回归分析、相关分析为工具，从弹性和边际的角度，从全部商品和一级大类商品分析研究打折力度与销售额、利润率的关系，为商场定价提供决策支持。

为了简化问题，作如下假设：

（1）该商场提供的数据具有代表性，且不存在系统误差和登记误差。

（2）在计算营业额的时候仅考虑商品销售收入，而不考虑补贴等其它收入，即营业额就是销售额。

（3）在计算成本的时候仅考虑商品的成本，而不考虑税金、管理费用等其他成本。

（4）利润是指纯利润，利润率是指成本利润率而不是销售利润率，成本利润率的定义：

1.1 每天营业额、利润率和折扣率统计

设某天第i个商品销售记录的销售数量、门店价、销售价和成本价分别为ni，p1i，p2i，ci，m为这一天销售记录的个数，则这天的营业额为

当天的成本额为

当天的成本利润率为

利润率λ∈[0，+∞)。

当天的预售额为

当天的折扣率为

折扣率γ∈(0，1)，折扣率越大，打折力度越大；反之，折扣率越小，打折力度越小。可见，折扣率是打折力度的一个测度指标。

计算结果如表1所示。

表1 商场每天的折扣率

1.2 建立销售额与折扣率的双对数回归模型

1.2.1 回归模型简介[7]

多元线性回归模型的一般形式为

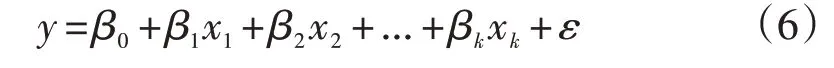
其中，β0称为回归常数，βj（j=1,2,...,k）称为回归系数，ε～N(0,σ2)且相互独立。

参数估计使用普通最小二乘法，精度检验使用拟合优度检验，系数检验使用t 检验，线性检验使用F检验。

估计的回归方程为

多元双对数回归模型的一般形式为

令Y=lny，Xj=lnxj，则式（8）就转化为式（6），于是就可以使用多元线性回归模型的参数估计和检验方法了。

估计的双对数回归方程为

1.2.2 边际分析

在经济学中，边际分析法是最基本的科学的分析方法之一，其数学原理很简单，对于离散情形，边际值为因变量变化量与自变量变化量的比值；对于连续情形，边际值为因变量关于自变量的导数值。边际的含义是因变量关于自变量的变化率，或者说是自变量变化一个单位时因变量的改变量。在经济管理研究中，经常考虑的边际量有边际收入、边际成本、边际产量、边际利润等。[8]

在多元线性回归方程（6）中，y关于xj的边际为

它表示，y关于xj的变化率为；或者当xj的增量Δxj=1时，y的增量Δy=。

1.2.3 弹性分析

在经济学中，弹性是指一个变量相对于另一变量发生的一定比例的改变的属性，可应用在所有具有因果关系的变量之间。在经济管理研究中，经常考虑的弹性有需求价格弹性、供给价格弹性、需求收入弹性、需求交叉弹性等。[9]

由多元双对数回归方程（9）得

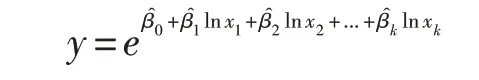
于是y关于xj的弹性为

可见，回归系数的实际意义就是弹性，其经济意义是：如果xj变化1%，那么y变化。

1.2.4 实证分析

根据表1 的数据，将销售额转化为以“万元”为单位，以折扣率为横坐标，以销售额为纵坐标，画散点图，如图1所示。

图1 折扣率与销售额的散点图

从图1 可以看出，存在一些奇异点，于是根据3σ原则，将[μ-3σ,μ+3σ]之外的折扣率或销售额剔除，再画散点图，如图2所示。

图2 剔除奇异点后的散点图

从图2 可以看出，销售额与折扣率呈现线性正相关关系，并且随着折扣率的增大，销售额呈现快速增大的现象，故考虑建立一元线性双对数回归模型。另外，这些点比较分散，这是由于在节假日、促销日举办了促销活动所致，因此以7 天为周期，分别对折扣率和营业额作移动平均处理，在此基础上进行参数估计。

给定显著性水平0.05，使用最小二乘法进行参数估计，结果如表2所示。

表2 参数估计及其检验结果

从表2 可知，参数的95%置信区间不包含0，故参数检验通过。拟合优度R2=0.277 5，表明拟合精度较低；F检验的相伴概率p=0.000 0 ＜0.05，表明lny与lnx的线性关系显著成立。于是有

根据公式（11），销售额关于折扣率的弹性值等于2.039 6 ＞1，表明销售额关于折扣率是富有弹性的，具体来说，当折扣率增加1%，销售额就增加2.039 6%。可见，加大打折力度会显著增加销售额，说明“薄利多销”有效。

1.3 建立利润率与折扣率的线性回归模型

根据表1 的数据，以折扣率为横坐标，以利润率为纵坐标，画散点图，如图3所示。

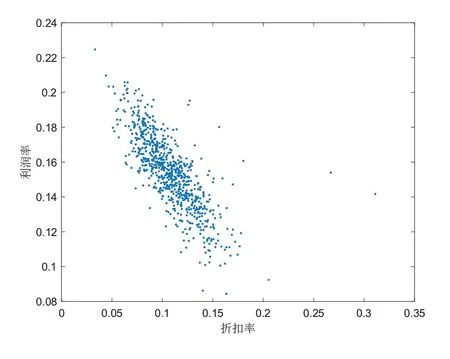
图3 折扣率与利润率的散点图

从图3 可以看出，存在一些奇异点，于是根据3σ原则，将[μ-3σ,μ+3σ]之外的折扣率或销售额剔除，再画散点图，如图4所示。

从图4 可以看出，这些点比较集中，可以进行参数估计。

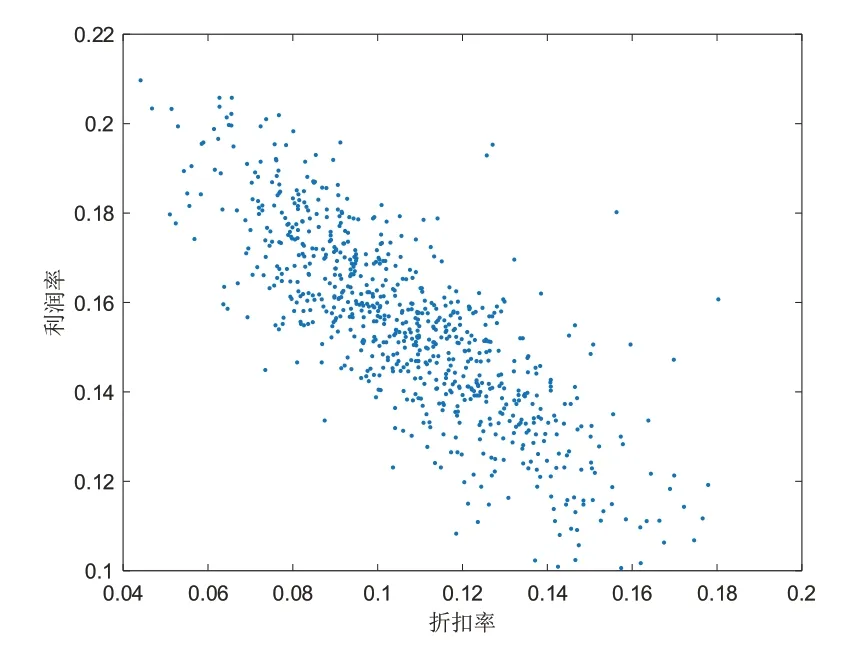
图4 剔除奇异点后的散点图

给定显著性水平0.05，使用最小二乘法进行参数估计，结果如表3所示。

表3 参数估计及其检验结果

从表3 可知，参数的95%置信区间不包含0，故参数检验通过。拟合优度R2=0.741 6，表明拟合精度较高；F检验的相伴概率p=0.000 0 ＜0.05，表明y与x的线性关系显著成立。于是有

根据公式（12）可知，利润率关于折扣率的边际值为-0.753 1 ＜0，它表示，如果折扣率提高1个单位(百分点)，那么利润率下降0.753 1 个单位（百分点），说明“打折让利”有效。

2 按照商品大类研究“薄利多销”的有效性

该商场把所有商品按照一级分类、二级分类、三级分类进行划分，其中一级类目有29类，这里仅选择热门商品作研究。根据商品销售记录表，统计出每一类商品的销售记录总数，记录总数较多的商品就是热门商品。

下面以一级类目商品为例进行“薄利多销”的有效性研究。

统计29个一级类目的销售记录数量，然后选择销售记录数量最多的10个类目，如表4所示。

表4 销售记录数量最多的10个类目

2.1 建立热门商品折扣率与销售额的函数关系

使用双对数回归模型，给定显著性水平0.05，参数估计与显著性检验结果如表5所示。

表5 双对数回归模型的参数估计与显著性检验结果

从表5 可知，所有参数检验获得通过。线性关系检验结果如表6所示。

表6 双对数回归模型的线性关系检验结果

从表6 可知，所有热门商品的双对数回归模型的线性关系检验获得通过，回归方程成立。不过，有些商品的拟合优度较低。

根据表5 中各个热门商品的斜率值，即可得出销售额关于折扣率的弹性，如表7所示。

从表7可得出以下结论：

表7 热门商品的弹性分析结果

（1）只有“粮油副食”类是正富有弹性，这表明，销售额对折扣率很敏感，加大打折力度，会显著增加销售额。这是由于粮油副食是刚性需求商品，一旦遇到商场打折促销，顾客就不管是否当前需要都会购买的。

（2）只有“酒水饮料”类是负缺乏弹性，这表明，加大打折力度，虽然会降低销售额，但不是很敏感；这是由于酒水饮料的保质期比较短，商场打折促销意味着该商品即将过期，顾客反而不会购买了。

（3）对于其余8 类商品，均是正缺乏弹性，这表明，加大打折力度虽然会增加销售额，但不是很敏感。

2.2 建立热门商品利润率与折扣率的函数关系

使用线性回归模型，给定显著性水平0.05，参数估计与显著性检验结果如表8所示。

表8 线性回归模型的参数估计与显著性检验结果

从表8 可知，所有参数的检验获得通过。线性关系检验结果如表9所示。

从表9 可知，所有热门商品的回归模型的线性关系检验获得通过，回归方程成立。

根据表8 中各个热门商品的斜率值，即可得出利润率关于折扣率的边际，如表10所示。

从表10可得出以下结论：

表10 热门商品的边际分析

（1）所有一级类目的商品的边际值均是负的，这表明，如果折扣率增加，那么利润率就会下降。

（2）“肉品”类的边际值最小，是-1.423 0，这表明，如果折扣率增加1个单位（百分点），那么利润率就会下降1.423 0个单位（百分点）。

3 研究结论和建议

3.1 研究结论

本文以国内某超市商品的实际销售记录为依据，以大数据分析为手段，采用实证研究方法，建立了销售额关于折扣率的双对数回归模型、利润率关于折扣率的线性回归模型，获得了以下结论：

（1）从整个商场层面分析，销售额关于折扣率的弹性值等于2.039 6 ＞1，是富有弹性的，加大打折力度会显著增加销售额，“薄利多销”有效。利润率关于折扣率的边际值为-0.753 1 ＜0，加大打折力度会减少利润率，说明“打折让利”有效。

（2）从一级大类的热门商品层面分析，销售额关于折扣率的弹性结果，“粮油副食”类是正富有弹性，“酒水饮料”类是负缺乏弹性，其余商品均是正缺乏弹性。所有热门商品的边际值均是负的。

3.2 建议

根据以上研究结论，针对超市商品制定“薄利多销”的价格策略如下：

（1）从整个商场来说，“薄利多销”策略是有效的，应该加大打折力度。

（2）对于一级大类的热门商品，“粮油副食”类要加大打折力度，“酒水饮料”类可适度缩小打折力度，其余商品可适度加大打折力度。