高原地区大气折光系数对三角高程观测影响的研究

李昌凯 钱俊锦

（1．中国水利水电建设工程咨询西北有限公司，陕西 西安 710100；2．四川中水成勘院测绘工程有限责任公司，四川 成都 610072）

0 概况

我国西部地区的某水电站，测区海拔约3000 m，属于典型高原气候，地势陡峭，人员通行极为不便，该监测项目的监测点布设在河流两岸，左右岸直线距离约1000 m，要从左岸观测点到达右岸观测点，所花费时间2h～3h，高原气象条件会发生明显改变，对高程观测造成不利影响。为提升工作效率，减少外界因素的影响，该项目的垂直位移监测采用单向三角高程测量。在进行三角高程测量计算时，大气折光系数是一个必要的参数。由于温度、气压等外界条件的变化，大气密度不均匀，人的视线或光学仪器的视线穿过大气层时，光会发生折射弯曲，该现象称为大气折光[1]。大气折光系数受气象、地区变化的影响很大，不同地区的折光系数难以用一个具体的数字代替。在不同地区，折光系数（k值）的差异量可以接近1，而测量规范的参考值通常为0.13～0.14，如果采用规范值进行三角高程计算，在一些特殊地区，极有可能会造成数据失真，因此，实际工作中将k值作为一个参数更恰当[2]。

1 三角高程测量原理

三角高程测量是根据全站仪观测得到的竖直角、距离、仪器高以及目标高等对两点间高差进行测量的一种测量方法，其易于操作，效率高，是目前高程观测的主要手段之一。其具体操作方法如下：在A点架设全站仪，B点架设棱镜，通过全站仪观测A、B两点之间的竖直角（或天顶距），距离，并分别记录A点和B点的温度、气压，最后根据两点的相对位置关系使用几何方法对高差进行计算，如公式（1）所示[3]。

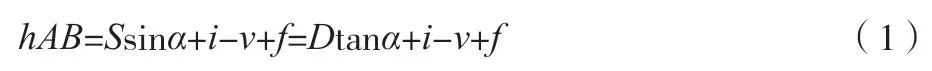
式中：S、D分别为两点间的斜距和平距；α为两点间视线的竖直角；i为仪器高；v为目标高；f为球差改正数p与气差改正数r之和。f=p+r=（1-k）（Scosα）2/（2R）=（1-k）D2／（2R）；k为大气折光系数；R为地球的半径。

由公式（1）可知，三角高程的误差来自于距离观测误差、竖直角观测误差和大气折光影响。可以通过采用高精度仪器、多次测量求平均值等方法减少距离和竖直角的观测误差，而大气折光是一种光学现象，其大小不受观测仪器和观测次数的影响，因此，提高单向三角高程测量的精度关键是减弱大气折光对观测结果的影响[4]。

2 折光系数对高程精度的影响分析

通过该文可知，三角高程单向观测的结果受折光系数影响很大，为研究折光系数在观测中对高程精度的影响，并且验证单向观测的可行性，决定通过单向观测和对向观测2种方法对同一监测点在一个连续的周期内进行三角高程测量，并对该观测周期内的高差变化值、k值变化值进行比较。通常情况下，全站仪距离测量的精度很高，受气象条件的影响较小，角度测量的精度则受气象条件影响较大，因此，为保证三角高程测量的精度，在距离测量精度一定的情况下，应尽量提高角度测量的精度，根据有关文献[5]，观测中应采用测角精度达到DJ05（“D”、“J”分别代表“大地测量”、“经纬仪”，05代表其角度测量精度达到0.5″）级的高精度的全站仪。经过对比，该项目决定采用采用瑞士LEICA（徕卡）公司生产的TM30型全站仪观测，TM30全站仪测角系统精度达到DJ05级，测距系统精度达到Ⅰ级，该型全站仪在精密测量领域应用广泛，其具备自动寻找棱镜观测和自动记录的功能，超限时自动重测，由于排除了人工观测时容易出现的肉眼观测角度倾斜造成的观测误差，因此其观测数据可靠性好，精度很高。其主要参数见表1。

表1 TM30型全站仪技术参数

根据相关的测量规范要求，确定观测测回数及观测限差：竖直角观测6测回（限差按三等三角高程），边长观测2测回（每照准1次读数4次）。单向观测和对向观测数据各自单独计算进行比较，计划观测4个观测日，第1和第2观测日之间、第3和第4观测日之间间隔2天，第2和第3观测日之间间隔10天。每测站往测4次，返测2次，各测次之间变换仪器高及棱镜高进行观测，以第1和第3次往测作为单向观测数据，第2和第4次往测及2次返测一同作为对向观测数据。观测限差见表2。

表2 边长及竖直角观测限差要求

本次观测一共选择5个监测点，点号依次为TP01～05；观测基点2个，点号为Ⅱ08、Ⅱ22，观测基点在不同的高程位置，以此来观察在其他外界条件基本相同时，不同俯仰角对折光系数的影响。Ⅱ08与监测点的垂直角约为-6°，Ⅱ22与监测点的垂直角约为36°。以Ⅱ08观测TP01、TP02；Ⅱ22观测TP03、TP04、TP05。观测过程的具体操作方法为：先在Ⅱ08架设全站仪，将仪器内的温度、气压设为标准值，即观测时先不对温度、气压进行改正，观测TP01、TP02的垂直角、斜距，并记录温度、气压、天气情况等气象元素，再分别在TP01、TP02架设全站仪观测Ⅱ08的垂直角、斜距，同样记录温度、气压、天气情况等气象元素；以此类推，对II22与TP03、TP04、TP05进行同样的观测。

折光系数如公式（2）所示[6]。

式中：k为折光系数；h1、h2分别为进行折光系数高差改正之前的往、返测高差；R为地球曲率半径；D为往返测平均平距。

根据公式（2）和实际观测数据对两点之间进行折光系数计算，再用实际计算的折光系数对观测高差进行改算，为比较折光系数的变化对高差观测值的影响，对每组观测数据的折光系数减0.1之后再次观测的高差进行计算。

0.1对高差观测值的影响。观测值的统计见表3～表6。

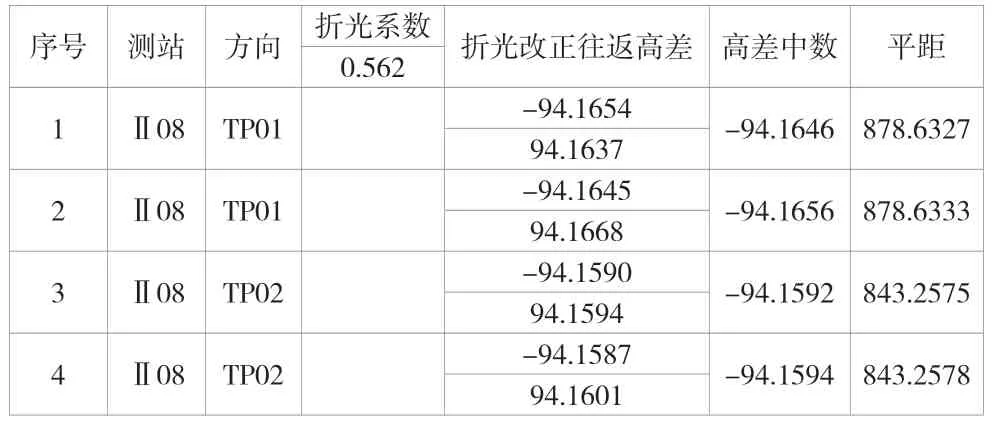
表3 Ⅱ08对向观测高差成果表

对比表3和表4的往测数据，当平距为850m左右时，折光系数变化0.1，对高差的影响为5mm（94.1637m-94.1689m=-0.0052m）；对比表5和表6的数据，当平距达到1000m时，折光系数变化0.1，对高差的影响可以接近1cm（522.6747m-522.6836m=-0.0089m），由此可以看出，当测点距离较远时，折光系数的变化对单向三角高程观测的结果有较大影响。同时可以看出，观测的高差不同，计算的k值差异明显。

表4 Ⅱ08对向观测高差成果表（调整折光系数后）

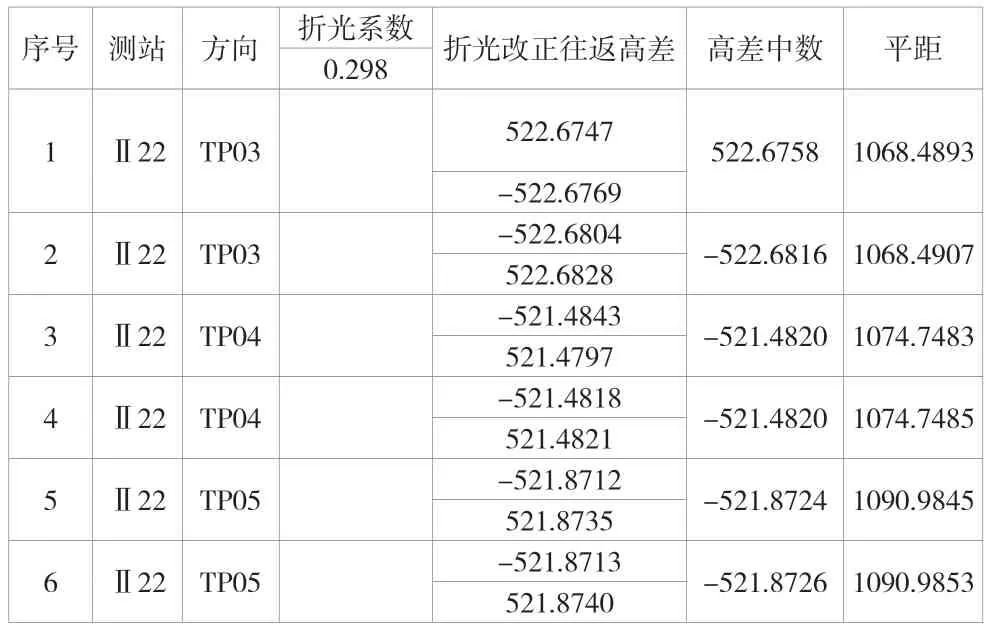
表5 Ⅱ22对向观测高差成果表

表6 Ⅱ22对向观测高差成果表（调整折光系数后）

3 单向观测中折光系数的选择

在选取折光系数时，一些规范和仪器设置多采用0.13～0.14，但是这显然与测区实际的情况出入较大。根据表3与表4，表5与表6的观测值之间的对比，当折光系数每变化0.1时，在较长（800 m及以上）的观测距离上，折光系数对高差观测的影响将超过5 mm，根据相关规范，垂直位移的监测，其工作基点的中误差要求不大于±3 mm，对垂直位移监测通常要求能反映6 mm左右的位移变化，折光系数对高差观测值的影响已达到不可忽略的程度，对该项目，如果采用规范中的k值，将使三角高程测量结果完全错误，因此，根据实际折光系数对观测高差进行计算就显得尤为重要。

为进一步研究折光系数随气象条件变化而变化的规律，确定折光系数的最佳取值范围，将4次观测计算得出的k值进行统计，统计结果见表7。再对该时间段内的温度和气压变化对比分析，以分析气象元素对折光系数的影响，温度和气压的变化统计见表8，其中温度以摄氏度为单位，气压以百帕为单位。

这其中，Ⅱ08与监测点的垂直角为-6°，从表7和表8可以看出，Ⅱ08与监测点之间的温度最大变化量为2℃，气压的最大变化值为400 Pa，折光系数的最大变化量为0.028；Ⅱ22与监测的垂直角为36°，与监测点之间的温度最大变化量为4.3℃，气压的最大变化值为700 Pa，折光系数的最大变化量为0.073。

表7 折光系数变化统计表

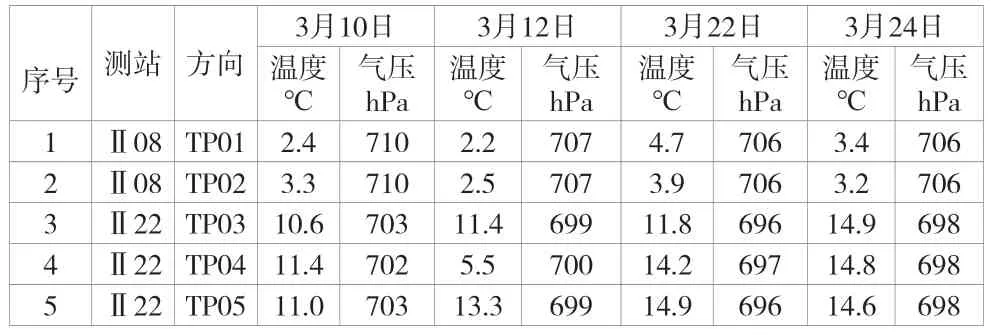
表8 温度气压变化统计表

由此可见，折光系数的变化受外界气象条件（主要指温度和气压）的变化影响较明显，当气象条件变化较小时，折光系数变化较小，气象条件变化大时，折光系数变化也较大。

综合表7的计算结果，在对单向观测高差进行计算时，以多个观测日的平均折光系数对观测数据进行计算，其中以II08为基点的观测数据的折光系数取值0.57，Ⅱ22为基点的取值0.28。再次对观测数据进行计算整理，分别得到4次单向观测和对向观测的高差变化值。单向观测高差变化值统计见表9，对向观测的统计见表10。

表9 单向观测高差变化表

表10 对向观测高差变化表

为进一步比较单向观测和对向观测在一个时期内的变化情况，用3月24日的数据减3月10日的数据得出累计变化量，再分别将单向和对向观测的累计变化量进行比较。比较结果见表11。

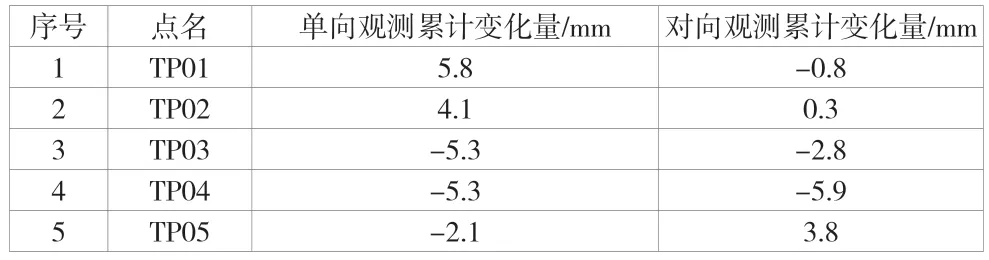
表11 单向和对向观测累计变化量对比表

从表9、表10可以看出，选择合适的折光系数后，观测结果单向观测和对向观测值的变化值差异较小。而根据表11，分别比较单向观测和对向观测，所有观测点位的累计变化量均在±6 mm（未超过2倍中误差）内，观测值的变化量为测量误差，即单向观测和对向观测的结论一致：所有点位无明显位移。所以，在内业计算时采取合理的折光系数，对监测点的垂直位移是可以通过单向观测的方法反应出来的。

4 结论

根据以上统计结果分析可知，在高原地区，由于条件所限，难以保证实时对向三角高程观测，因此为提高工作效率，需要采取单向观测时，为保证单向观测中三角高程的观测精度，应注意以下4点：1）为提高角度和距离的测量精度，应采用具备自动观测记录功能的高精度全站仪。2）长距离的三角高程测量不能采用固定的k值进行高差计算。3）利用对向观测测定出一段时间内（7天左右）的本测区折光系数，在温度气压变化不大时，使用该折光系数进行单向三角高差观测。或者在同一区域不同点位之间选取区域中心的点进行对向观测，将该对向观测计算得到的折光系数应用于其他点的单向观测数据处理中。4）观测基点与被观测点的高差不宜过大，俯仰角度尽量不大于±10°。