单轴压缩固化泥炭土的弹塑性损伤模型试验研究

申林方，何仕娟，王志良，陈玉龙

(昆明理工大学建筑工程学院，昆明 650500)

0 引 言

在昆明滇池盆地分布着发育范围广、深度大且成分复杂的泥炭土层，该土层具有有机质含量高、天然含水率高、孔隙比大、压缩性大、强度低等特征[1]。在工程建设中遇到泥炭土层时，常出现工后沉降过大、失稳破坏等病害[2]，故将其作为承载地基时须进行加固处理。因此，研究固化泥炭土的损伤破坏机制，具有非常重要的理论意义和工程应用价值。

随着深层搅拌桩、高压旋喷桩等土体加固方法的广泛应用，国内外学者针对土体固化机理、固化土体的本构关系等开展了大量的研究工作，并取得了丰硕的研究成果。在土体固化机理研究方面，黄新等[3]考虑孔隙填充和土颗粒的胶结作用，提出了固化土结构的形成模型。宁建国等[4]通过化学试剂改变土样的pH值，研究了pH值对固化土抗压强度的影响。张立力等[5]研究了高镁镍渣-磷石膏基胶凝材料固化盐渍土的工程性能和理化性能，并分析了固化作用机制。邓永锋等[6]研究了地聚合物-偏高岭土对水泥土力学性能的影响，并讨论了其改善水泥土强度的机理。然而，泥炭土中富含的有机质具有一定的物理化学活性，会阻碍或延缓水泥水化反应，从而影响固化结构的形成[7]。为此，陈慧娥等[8]从易溶盐、阳离子交换容量及微观结构等方面，研究了有机质在水泥加固软土中的作用机制。Zhang等[9]通过试验证实了矿物钙矾石的生成有利于填充土体孔隙，从而提高固化有机质土的强度。王志良等[10]针对红黏土局部置换后的泥炭土进行了水泥加固试验，并从宏观和微观角度研究了泥炭土的固化机理。Wong等[11]将硅砂作为填料,偏高岭土作为火山灰材料,水泥作为胶结材料对泥炭土进行了加固试验，其无侧限抗压强度得到了显著提高。由于泥炭土特殊的物理力学性质，在有机质的影响下其固化机理与常规的土体有显著差异。为满足工程建设的需要，目前的研究成果主要侧重于从力学特性出发研究固化泥炭土的优化配比，忽视了不同配比下其应力-应变的演化规律。

在固化土体的本构关系研究方面,童小东等[12]基于简化水泥土应力-应变曲线“弹塑性耦合”的特性，建立了水泥土的弹塑性损伤模型。王立峰等[13]建立了水泥土的损伤演化方程，并结合试验验证了其有效性。刘忠等[14]基于SMP(spatially mobilized plane)准则实现了修正双屈服面模型的三维化，并结合水泥砾质土的三轴试验结果对该模型进行了初步验证。王军等[15]基于不排水三轴压缩试验研究了水泥土的刚度软化规律，得到了修正的邓肯-张模型。孙凯等[16]基于统一硬化模型和非关联的流动法则，建立了描述改良土体力学特性的弹塑性本构模型。泥炭土分布范围相对较少，且具有显著的区域性特征，虽然泥炭土固化技术得到了广泛应用，但针对其本构关系的研究却鲜有报道，这极大地限制了泥炭土改良技术的持续性发展。

鉴于此，本文将机制砂作为填充材料，水泥和磷石膏作为胶结材料，对泥炭土进行固化试验研究。基于无侧限抗压强度试验和单轴循环加-卸载试验，讨论了泥炭土的固化效果。在此基础上，引入材料的损伤理论，建立了单轴压缩状态下固化泥炭土的弹塑性损伤模型。

1 实 验

1.1 试验材料

试验所用泥炭土取自云南昆明某地铁车站，取土深度为10 m，土样的物理力学指标如表1所示。泥炭土为黑灰色，由于受到有机质的影响，土质疏松，呈弱酸性，且天然含水率较高，天然密度和干密度小，孔隙比较大。

表1 天然泥炭土物理力学指标Table 1 Physical and mechanical indexes of natural peaty soil

为了提高泥炭土的强度，本文从胶结和填充两个方面出发，对其进行加固处理。胶结材料主要选用水泥和磷石膏，将水泥作为主要胶凝硬化组分材料，用于胶结固化体系中的土颗粒，以达到提高土体强度的效果。工业废料磷石膏主要成分为二水磷石膏(CaSO4·2H2O)，用于提高固化土体的早期强度，并促进膨胀性水化产物钙矾石的生成。填充材料选用机制砂，其主要成分为SiO2，粒径在0.075～2 mm之间。

1.2 试验方案

为了分析不同水泥掺量对泥炭土的固化效果，本试验水泥掺量C选为天然泥炭土质量的10%、20%及30%，水灰比设为1.0。磷石膏的掺量P分别设为水泥质量的0%、15%和30%。作为填充材料的机制砂，其掺量为天然泥炭土质量的30%。

试样制备过程为：(1)根据试验方案称取合适质量的泥炭土、填充材料、固化剂及水；(2)将称取的材料放入JJ-5型水泥胶砂搅拌机中搅拌10 min；(3)将拌合物分三层插捣装入70.7 mm×70.7 mm×70.7 mm模具，并采用保鲜膜覆面以防止水分蒸发；(4)1 d后拆除模具，并将试块浸水养护28 d。

针对不同配比的固化土体试样开展无侧限抗压强度试验，用于探讨泥炭土的固化效果和确定固化泥炭土的极限荷载和弹性比例极限。对固化泥炭土试样进行扫描电镜观测，便于从微观角度分析其填充效果和固化机理。此外，为了获取所建立固化泥炭土弹塑性损伤本构模型的待求参数，在弹性比例极限和极限荷载之间设置5次加-卸载，开展相应的循环加-卸载试验。所开展试验的详细过程如下：

无侧限抗压强度试验：采用万用伺服液压机进行加载，加载速率设为1.414 mm/min。该设备同时配有全自动数据采集仪，可记录加载过程中的荷载与位移。

扫描电镜测试：在干燥后的试样表面取一光滑的微小样本，并用导电胶将其粘附于支座上，然后在抽真空装置中喷金90 s，最后采用钨灯丝扫描电镜VEGA3进行微观形貌观测。

单轴循环加-卸载试验：试验设备为万用伺服液压机，加载速率由应变控制，设为1.414 mm/min，卸载速率由应力控制，设为5 N/s。当加载值达到卸荷应力时发生卸载,当卸荷至0 N时则一个循环结束，并自动进入下一级循环加-卸载。

2 结果与讨论

2.1 无侧限抗压强度

不同配比下固化泥炭土的无侧限抗压强度如图1所示，由图可知,磷石膏掺量分别为0%、15%及30%时，固化泥炭土的无侧限抗压强度均随着水泥掺量的增加而增大，且两者近似呈线性变化。同时，磷石膏的掺入可显著提高固化泥炭土的强度，且磷石膏掺量从0%增加至15%时，强度增加显著，而从15%增加至30%过程中，强度则增长缓慢。这主要是由于：适量的磷石膏能够促进水化反应，并生成具有膨胀性的针状或棒状钙矾石，有利于填充孔隙，起到支撑骨架的作用，并提高固化泥炭土的强度；磷石膏过量时，钙矾石的膨胀作用会破坏水化硅酸钙形成的固化结构，在一定程度上对固化土体起到相反的作用。当水泥掺量为30%时，P=0%的固化泥炭土强度为172.2 kPa，P=15%、P=30%的固化泥炭土强度分别为220.6 kPa、228.1 kPa，后两者固化泥炭土所获得的强度分别是纯水泥固化的1.28倍和1.32倍。因此，在利用水泥加固泥炭土时，合适的磷石膏掺量有利于提高固化泥炭土的强度。图2为固化泥炭土的典型应力-应变曲线。由图可知，随着水泥掺量的增加，固化泥炭土的刚度逐渐增加，且达到破坏时的应变逐渐减小，当磷石膏掺量为15%，水泥掺量分别为10%、20%及30%时，极限荷载所对应的应变分别为4.57%、3.99%和3.22%。

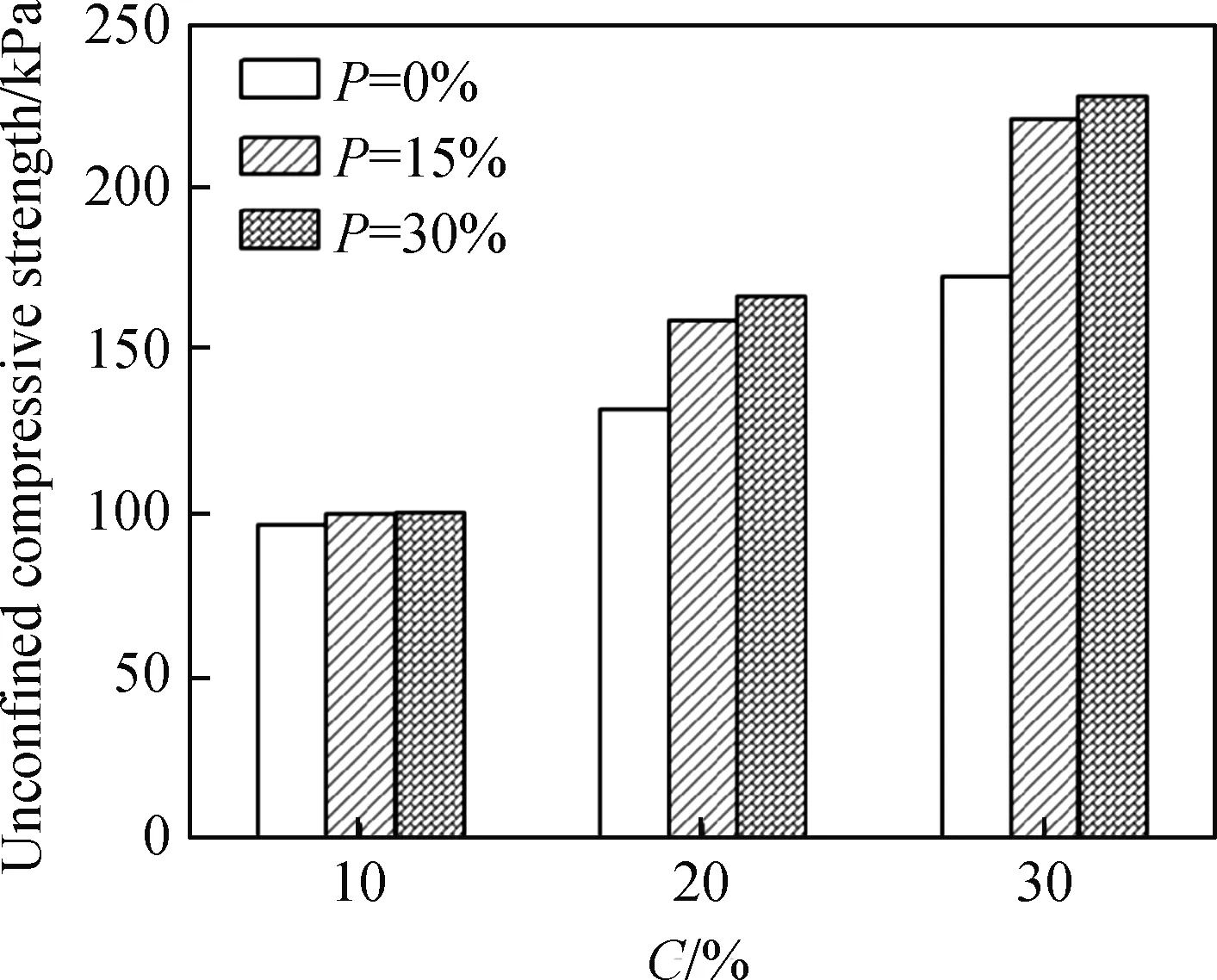
图1 固化泥炭土的无侧限抗压强度Fig.1 Unconfined compressive strength of stabilized peaty soil

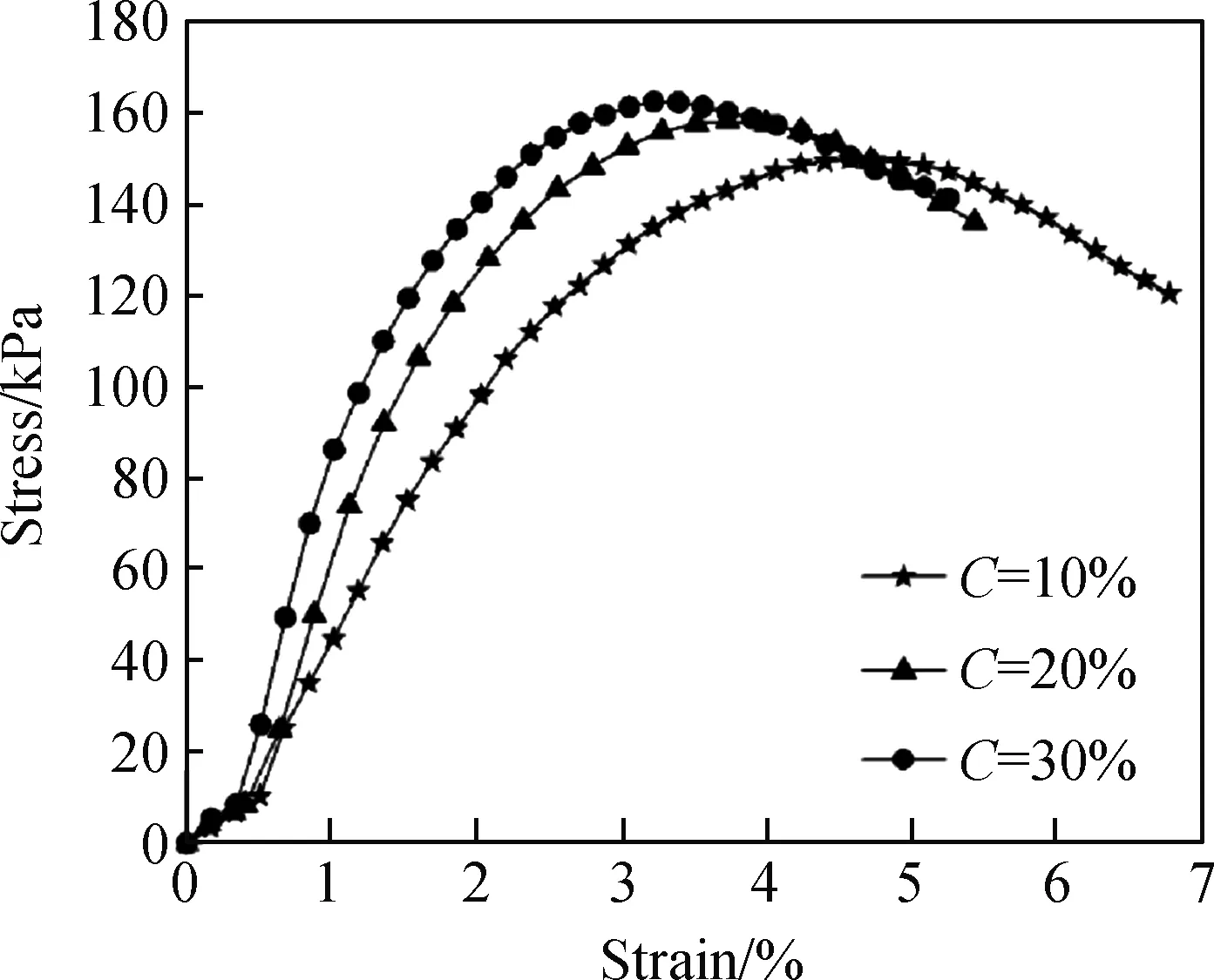
图2 当P=15%时固化泥炭土的应力-应变曲线Fig.2 Stress-strain curves of stabilized peaty soil with P=15%

2.2 扫描电镜分析

对水泥掺量为30%，磷石膏掺量为0%、15%和30%的固化泥炭土试样进行扫描电镜观测，试样的微观结构如图3所示。由图可知，在磷石膏掺量为0%时，固化土体的微观结构中存在大量的孔隙及疏松的架空结构，同时存在一定量的针状、细棒状钙矾石和CaCO3晶体。随着磷石膏掺量增加，粗棒状及块状的结晶体有所增加，粗棒状钙矾石穿插于固化泥炭土的疏松大孔隙中，形成结晶网状稳定结构，使得试样的微观结构更加密实，表明磷石膏的掺入能够促进钙矾石的生成，并提升固化土体结构的密实度，有助于提高固化土体的强度。

图3 当C=30%时固化泥炭土的微观结构Fig.3 Microstructure of stabilized peaty soil with C=30%

2.3 单轴循环加-卸载试验分析

由无侧限抗压强度试验可得到各工况下的极限荷载σf，并可确定弹性比例极限σd=βσf，其中β为系数常量，取值范围一般为0.7～0.8。根据固化泥炭土无侧限抗压试验得到的应力-应变曲线，可以确定本文的β=0.72。为了建立固化泥炭土的弹塑性损伤模型，在塑性变形阶段，即在βσf～σf区段，设置5次循环加-卸载试验，卸载应力分别取极限荷载的75%、80%、85%、90%及95%，并得到相应的应力-应变曲线。

图4为磷石膏掺量15%时，固化泥炭土在单轴循环加-卸载作用下的应力-应变曲线。从图中可看出，随着水泥掺量的增加固化泥炭土抗压强度逐渐增大，弹性模量也相应增大，且能够承受更高的循环加载力。同时，随着水泥掺量的增加，试样达到卸荷应力所引起的应变逐渐减小。当水泥掺量为10%、20%及30%时，第1级卸荷应力所对应的应变分别为1.61%、1.43%及1.17%，且在经历多次加-卸载后，仍有相似的趋势,这说明随水泥掺量的增加，固化泥炭土的抗压强度逐渐提高，且试样有向脆性破坏转化的趋势。由于卸荷应力大于弹性比例极限，故在每级卸载阶段均会伴随塑性变形的产生，从而导致滞回曲线表现为下部不闭合的新月形。从图中还可以看出：在第1次和第5次的加-卸载循环中，滞回曲线的不闭合区域面积大于其他循环，这说明固化泥炭土在塑性开始阶段和接近破坏阶段的加-卸载循环过程中，会产生较大的塑性变形，并产生较多的能量损耗，这与文献[17]的试验结果相类似。

图4 当P=15%时固化泥炭土的单轴循环加-卸载应力-应变曲线Fig.4 Stress-strain curves of stabilized peaty soil with P=15% under uniaxial cyclic loading and unloading

3 固化泥炭土损伤模型的建立

由于微孔洞、微裂纹等结构微缺陷的存在，构件有效承载面积减小，单位面积上的有效应力增大，则：

(1)

式中:σ为名义应力；A0为名义面积；σv为有效应力；Av为材料的有效承载面积。

为了表征构件在破坏过程中的裂纹扩展和有效承载面积的减小，引入损伤变量D：

(2)

则：

σ=σv(1-D)

(3)

基于应变等效原理，可得损伤后的本构方程[18]：

(4)

式中:ε为材料无损时的应变；E为材料无损时的弹性模量。

假定Ev为材料受损时的弹性模量，则损伤变量与弹性模量间的关系为：

(5)

固化土体在单轴压缩情况下，应变量ε1由弹性应变εe与塑性应变εq构成：

ε1=εe+εq

(6)

对于固化泥炭土这类弹塑性材料，其内部的损伤主要是由单轴压缩状态下裂隙的形成、发展、贯穿形成。根据弹性等效性假设，可推导出三维状态下固化土体的损伤变量D1[19]：

(7)

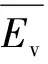
(8)

将式(8)代入式(7)，可得：

(9)

假定固化土体有效应力σv与有效塑性应变εvq服从弹塑性演变规律：

σv=σd+a(εvq)b

(10)

式中：a、b是待定常数。

有效塑性应变εvq可表示为：

εvq=(1-D1)εq

(11)

基于微元损伤理论，单轴压缩条件下的损伤演化方程为：

D1(ε1)=1-exp[-γ(ε1-εd)]

(12)

式中:γ为材料常数；εl-εd为塑性阶段开始后的应变增量，其中εd为材料开始产生塑性变形时对应的应变值。

综上，可得到单轴压缩条件下固化泥炭土的损伤本构方程：

(13)

D1(ε1)=1-exp[-γ(ε1-εd)]

(14)

由式(13)、(14)可知，建立固化泥炭土的弹塑性损伤本构模型，需得到E、a、b、γ及εd5个待定参数。为此，本文根据无侧限抗压强度及单轴循环加-卸载的试验结果，对其进行计算求解。

4 损伤模型参数的确定

4.1 弹性模量

无损状态下固化泥炭土的弹性模量E可由第1级荷载得到的应力-应变曲线求得。根据不同试验方案求得的固化泥炭土弹性模量E如表2所示。由表可知：当磷石膏掺量一定时，固化泥炭土的弹性模量随着水泥掺量的增加而增大，这与固化土体的无侧限抗压强度表现出一致的变化规律；而当水泥掺量一定时，磷石膏掺量从0%增加至15%时，固化泥炭土的强度增长显著(水泥掺量为20%和30%时)，弹性模量也增加较大，而从15%增加至30%的过程中，强度增长缓慢，弹性模量则变化不大，甚至略有减小，这可能是由于磷石膏对水泥水化的缓凝作用。

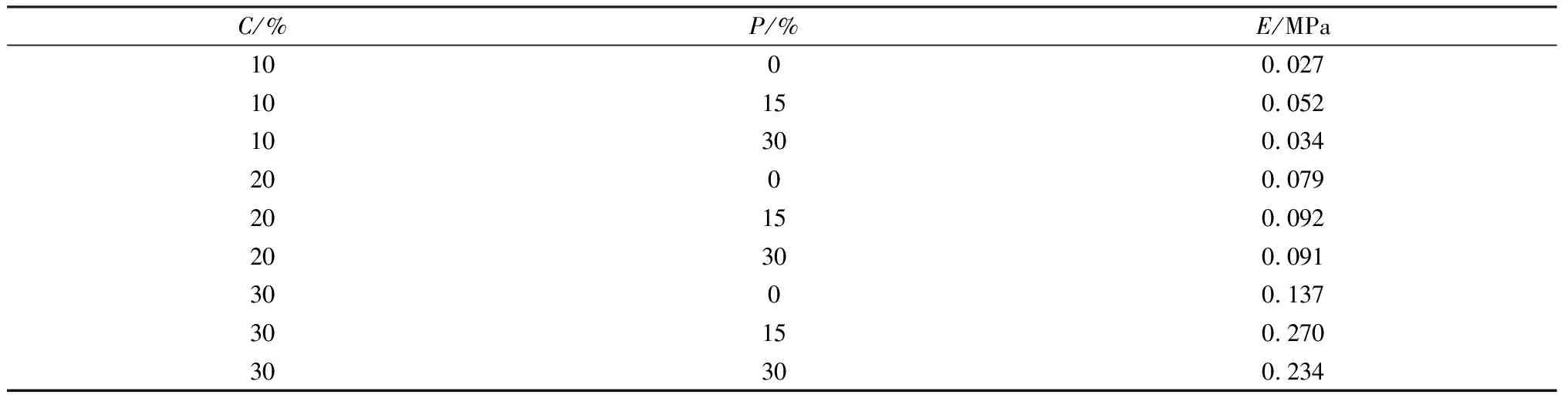
表2 固化泥炭土的弹性模量汇总Table 2 Elastic modulus summary of stabilized peaty soil

4.2 塑性损伤参数

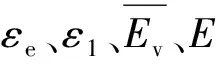
根据单轴循环加-卸载试验得到的应力-应变曲线，并结合式(9)可以求得不同固化泥炭土在各级荷载作用下的损伤变量D1和轴向应变ε1。假定固化泥炭土从弹性比例极限开始产生塑性变形，根据各级循环加-卸载试验分别得到的D1和ε1，以及当应力为βσf时所对应的ε1，结合式(12)进行曲线拟合，得到不同配比下的参数γ及εd。图6为当C=30%、P=15%时，D1与ε1的拟合曲线，表3中有不同工况下待定参数γ及εd的结果汇总。由表3可知，参数γ随磷石膏掺量及水泥掺量的增加而增大，这表明试样强度越高损伤越大，且在较小的应变下就能进入塑性损伤阶段，微裂隙快速扩张并贯穿整个截面，出现脆性破坏，反之，γ越小，土体损伤随应变的增大而演化的越慢，试样逐渐表现出延性破坏。

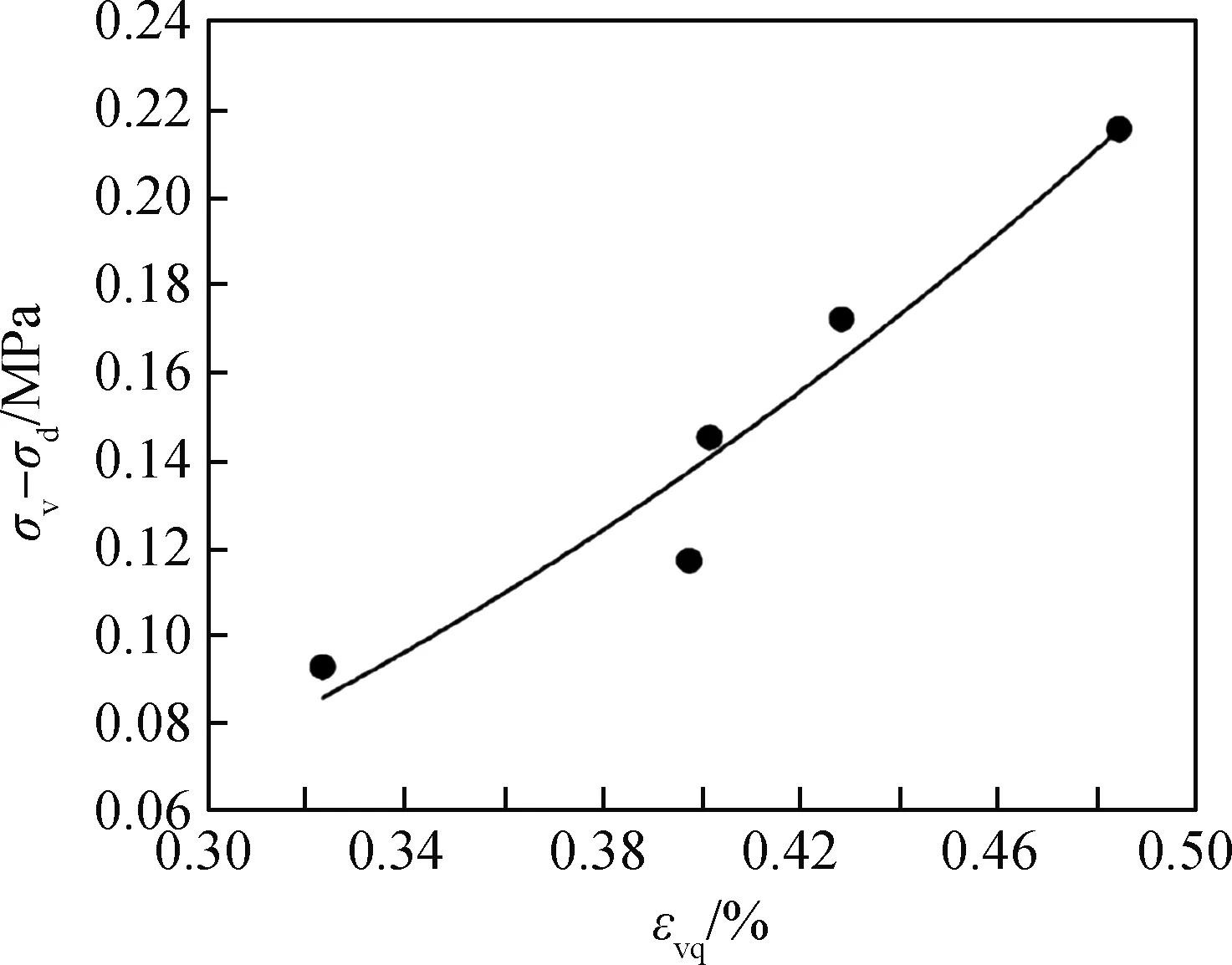
图5 当C=30%、P=15%时σv与εvq的拟合曲线Fig.5 Fitting curve of σv and εvq when C=30% and P=15%

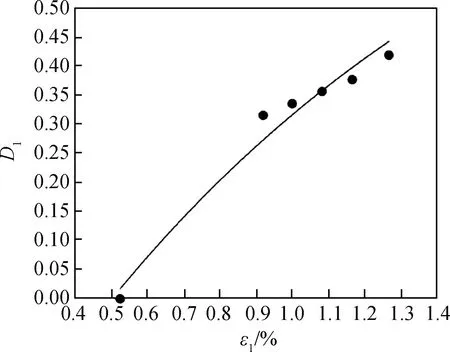
图6 当C=30%、P=15%时D1与ε1的拟合曲线Fig.6 Fitting curve of D1 and ε1 when C=30% and P=15%

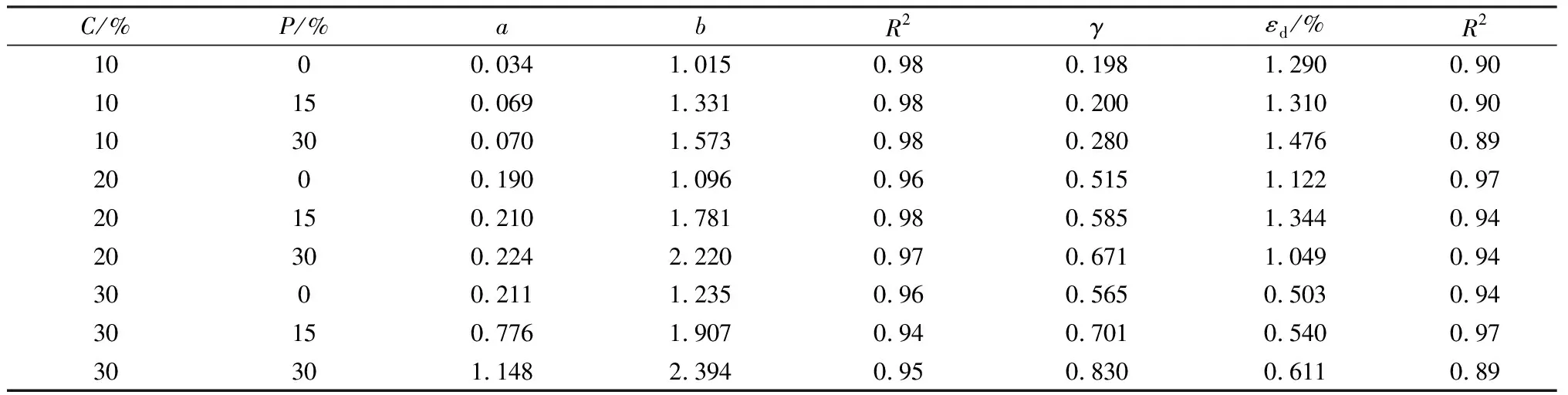
表3 待定参数的汇总Table 3 Summary of the unknown parameters

5 结 论

(1)固化泥炭土的无侧限抗压强度随水泥掺量的增加而增大，且两者近似呈线性关系；而随着磷石膏掺量的增加，固化泥炭土的强度增长速率则呈先增加后减小的趋势。

(2)在5次循环加-卸载试验中，第1次和第5次滞回曲线的不闭合区域面积大于其他循环，故固化泥炭土在塑性开始阶段和接近破坏阶段会产生较大的塑性变形，并产生较多的能量损耗。

(3)基于损伤理论和应变等效性假设，建立了单轴压缩状态下固化泥炭土的弹塑性损伤本构模型。根据单轴循环加-卸载(5级)的试验结果，求得了固化泥炭土弹塑性损伤本构模型的5个待求参数。

(4)本文所建立的本构模型具有较好的普适性，能够预测固化泥炭土的损伤演化过程以及无侧限抗压强度，对实际工程具有一定的指导作用。但由于泥炭土的物理力学指标波动范围较大，后续研究可根据泥炭土的物理力学指标以及外掺剂参数建立更加完善的理论模型。