不同巷道断面形状对围岩稳定性的数值模拟研究

段燕伟DUAN Yan-wei

（黑龙江科技大学，哈尔滨 150022）

0 引言

巷道断面形状是影响围岩稳定性的关键因素，不同的断面形状将影响巷道围岩的应力分布，从而产生不同的围岩状态。不同断面形状的巷道难以在同一地质条件下实现，而数值模拟可以轻松实现同一地质条件下不同工况的研究。因此借助数值模拟的手段，可以研究同一地质条件下不同巷道形状对巷道围岩稳定性的影响。

鉴于此，国内学者借助数值模拟软件做出了大量研究，姬书强[1]采用有限元软件，研究了围岩力学性能的影响。李晓斌[2]等通过数值模拟对矩形和直墙平顶肩角微拱形厚顶煤巷道应力分布特征进行了对比分析。程国栋[3]采用PFC 2D软件研究分析了6种不同断面形状的巷道围岩变形破裂特征。张一夫[4]等利用有限体积法对不同巷道断面形状的围岩进行数值模拟，并定量分析巷道断面形状对围岩的影响。张晓刚[5]等通过数值模拟和现场试验对深井软岩巷道的稳定性进行了研究，并由此提出了支护方案。郭晓菲[6]等结合蝶形破坏理论对不同巷道断面形状的适用性进行了探讨。刘康等[7]开展了临近爆破条件下巷道断面形状对围岩裂纹扩展规律的研究。董红娟[8]等利用FLAC3D数值模拟软件对巷道断面形状进行了模拟分析，得出最优巷道形状，并应用于现场。王克义[9]利用数值模拟手段对不同断面形状下巷道围岩的稳定性进行了分析，并提出合理的支护参数。王刚[10]模拟分析了三种不同断面形状巷道的破坏特征和围岩变形量，得出最优断面，并提出支护方案。张进鹏[11]等分析了大倾角煤岩层条件下，对半圆拱形、斜顶梯形以及偏心圆弧形巷道的围岩稳定性进行分析，并从耦合支护的角度，选择最优的巷道形状。李晓斌[12]等针对厚煤层矩形巷道支护困难的问题，利用数值模拟研究，改进了巷道形状，采用直墙平顶肩角微拱形，对支护难题有所改善。以上研究均针对某一种特定地质条件，利用数值模拟，从巷道围岩应力环境进行分析，但对于不同断面形状巷道围岩的应力、变形和塑性区域较为全面的研究相对不足。

本文为研究断面形状对巷道围岩稳定性的影响，利用数值模拟软件FLAC3D对矩形、梯形和直墙圆拱形三种断面形状的巷道进行了模拟，并全面分析了不同断面形状巷道围岩的应力特征、变形特征和塑性区域的分布规律，从而选取该地质条件下最佳巷道断面形状，为解决工程问题提供依据，同时为类似工程提供借鉴。

1 工程背景

红庆梁煤矿3-1煤层为主采煤层，厚度为4.7m～5.7m，平均煤厚为5.15m。煤层倾角为0-6°，平均倾角为3°。3-1号煤层结构简单，呈黑色，沥青光泽，参差状、棱角状断口，内生裂隙较发育，常为黄铁矿及方解石薄膜充填，条带状结构，属半暗型煤。局部含1层夹矸，厚度为0.15～1.0m，夹矸岩性为砂质泥岩或砂岩。

11303 综采工作面沿煤层倾向布置，工作面顺槽沿煤层走向布置。该工作面位于3-1煤辅助运输大巷西部，走向长为4290m，倾向长为275m。11303工作面回风巷顶板为细砂岩，呈灰色，局部含植物化石，平行层理发育；底板为泥岩，灰色，局部含植物化石，岩屑及云母碎片，泥岩胶结。在现有支护条件下，底鼓现象严重，影响正常生产。

2 模拟方案

本次数值模拟以红庆梁煤矿11303回风巷为工程背景，根据工程地质条件，建立模型。模拟区域为长×宽×高=50m×30m×45m，其中矩形巷道断面为宽×高=5.5m×4m，梯形巷道断面为上底/下底×高=4.5m/5.5m×4m，直墙圆拱形巷道断面为宽5.5m，拱形半径为2.75m，墙高为1.25m。模型网格采用“中间密四周疏”的划分原则，以底板左下角为坐标原点，倾向为x轴方向，走向为y轴方向，重力方向为z轴方向。

模型整体采用Mohr-Coulomb力学模型，巷道开挖采用null模型代替。该模型限制其侧向和底部处位移，在上表面施加12.2 MPa的等效荷载，模拟上覆岩体的自重条件。表1为围岩力学参数。模拟深入揭示不同巷道断面形状开挖稳定后围岩应力特征、变形特征、围岩塑性区分布规律。

表1 围岩力学参数

3 结果分析

3.1 巷道围岩应力特征

图1为不同形状巷道围岩垂直应力云图。由图可知，①不同形状巷道围岩垂直应力分布规律一致，巷道两帮为高应力区域，两帮以椭圆形式向两侧扩散；顶底板为低应力区域，以半圆的形式向两侧扩散，最终过渡为原岩应力区域。

图1 不同形状巷道垂直应力云图

②不同形状的巷道应力区域分布略有不同：就两帮高应力区域而言，矩形巷道高应力区域最大，直墙圆拱形巷道最小，梯形巷道居中；对于巷道顶底板的低应力区域因巷道形状而异，梯形巷道和直墙圆拱形巷道顶底板应力不对称，顶板低应力区域相对较小。

③不同形状巷道的应力峰值不同，矩形巷道高应力峰值为21.66MPa，梯形巷道为19.49MPa，直墙圆拱形为19.45MPa，应力集中系数从1.86降到了1.59。因此，巷道形状影响巷道围岩应力环境，三种巷道形状中，直墙圆拱形巷道两帮高应力区域最小，且高应力最大值较小；顶底板应力分布均匀，直墙圆拱形巷道更利于巷道稳定。

为分析巷道围岩的应力变化特征，分别沿巷道顶底板（中部）、右帮（距底板2m）、顶角和底角位置（与水平方向呈45°夹角方向），设置测线，侧线长度为15m，每隔1m设置一个测点。不同形状巷道条件下，不同位置的应力变化不同：顶、底板和右帮垂直应力变化规律相似，不同巷道的应力差值不大；巷道底角垂直应力变化为先增大后减小，梯形和直墙圆拱形巷道底角垂直应力变化规律相似，而矩形巷道底角垂直应力整体偏低；梯形巷道顶角垂直应力整体偏低，且在8m范围内远低于原岩应力，而直墙圆拱形巷道顶角相对稳定，有利于巷道的整体稳定。综上所述，从巷道应力分布来看，直墙圆拱形巷道应力分布较为均匀，高应力区域较小，整体稳定性最好。

3.2 巷道围岩变形特征

图2为不同巷道宽高比围岩垂直位移云图。由图可知，①巷道掘进稳定后，垂直位移分布呈对称分布，垂直位移主要发生在巷道顶底板。从分布范围来看，顶板分布范围较小，底板分布范围较大。从位移值上来看，顶板垂直位移较大。

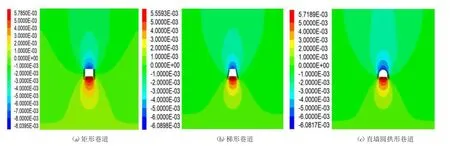
图2 不同形状巷道垂直位移云图

②对比三种巷道断面形状的垂直位移，矩形巷道顶板位移最大为8.04mm，梯形巷道和直墙圆拱形巷道顶板位移较小，分别为6.09mm和6.08mm。矩形巷道和直墙圆拱形巷道底板位移较大，分别为5.79mm和5.72mm，梯形巷道底板位移为5.56mm。综上所述，巷道形状对于巷道围岩变形有较大影响，直墙圆拱形巷道底板变形量相对较小，底鼓范围也相对较小，因此直墙圆拱形巷道围岩变形量最小，巷道围岩更稳定。

3.3 巷道围岩塑性区分布

图3为不同形状巷道塑性区域分布图。由图可知，①不同形状的巷道围岩塑性区破坏方式基本一致，破坏形态为“X”型，顶底板为拉伸破坏，巷帮及顶底角位置为剪切破坏。②与直墙圆拱形相比，梯形巷道和矩形巷道塑性破坏范围稍大，尤其体现在顶板和顶角位置，这与垂直应力分布结果一致，顶底角是巷道围岩变形破坏的关键位置。③整体来看，三种形状巷道底角的剪切破坏比较严重，直墙圆拱形巷道底角塑性区域相对较小，这是因为圆拱形巷道应力分布均匀，不易形成应力集中，从而使巷道围岩应力处于相对平衡的状态，不易发生较大范围的塑性破坏。综上所述，巷道形状为直墙圆拱形时，巷道围岩塑性区域最小，更有利于巷道围岩稳定。

图3 不同形状巷道塑性区域分布

4 结论及建议

①不同形状巷道的应力峰值不同，矩形巷道高应力峰值为21.66MPa，梯形巷道为19.49MPa，直墙圆拱形为19.45MPa，应力集中系数从1.86降到了1.59。巷道底角垂直应力变化为先增大后减小，梯形和直墙圆拱形巷道底角垂直应力变化规律相似，而矩形巷道底角垂直应力整体偏低；梯形巷道顶角垂直应力整体偏低，且在8m范围内远低于原岩应力，而直墙圆拱形巷道顶角相对稳定，有利于巷道的整体稳定。

②垂直位移主要发生在巷道顶底板。从矩形到梯形再到直墙圆拱形巷道，顶底板的位移范围变小，且垂直位移峰值也变大，底板垂直位移从8.04mm增加到6.08mm，顶板垂直位移从5.79mm降低到5.71mm。这表明直墙圆拱形巷道围岩变形量最小。

③巷道围岩塑性区破坏方式基本一致，顶底板为拉伸破坏，巷帮及顶底角位置为剪切破坏。与直墙圆拱形巷道相比，梯形巷道和矩形巷道塑性破坏范围稍大，尤其体现在顶板和顶角位置，且直墙圆拱形巷道顶板塑性破坏范围最小。

④通过从应力特征、变形特征和塑性区域分布三个方面，分析矩形、梯形和直墙圆拱形三种断面形状的巷道围岩稳定性，建议采用直墙圆拱形巷道，该形状断面巷道围岩稳定性最好，从模拟结果上来看，可以较好地解决底鼓问题。