基于SVM-MLP的乳腺癌预测

王德广， 黄盈朵

(大连交通大学，软件学院，辽宁，大连 116028)

0 引言

据国家癌症中心统计数据，癌症死亡占我国居民全部死因的23.91%[1]，俨然已成为人类健康路上的最凶猛的拦路虎之一。其中乳腺癌是最常见的女性癌症，现仍为女性发病首位，2012年在全球范围内乳腺癌大约占所有癌症的25%[2]，2018年的占比则为11.6%[3]。

随着机器学习和深度学习的发展，为医疗领域提供了极大帮助，医生使用训练好的模型辅助诊断病人是否患有癌症，提高工作效率和诊断准确性。现有很多机器学习分类算法可以解决这一类问题，但是这些算法各有不足，比如朴素贝叶斯算法，需要知道先验概率，先验模型设定的不准确很大程度上会影响预测效果。KNN算法在样本特征分布不平衡时对稀有类别的预测的准确率低等。本研究采用逻辑回归算法、支持向量机模型和前馈神经网络对带有标签值的乳腺癌特征数据进行预测分类，将支持向量机分类好的数据放入神经网络中减少神经网络迭代时间，并对准确率进行比较，同时使用神经网络对于医疗领域重视的漏报率进行预测分析。

1 逻辑回归算法

逻辑回归(logistic regression，LR)是一种理论上的线性回归分析实体模型(广义线性模型)，可用于解决大数据挖掘、疾病自动诊断、房价预测分析等问题。

对于给定的特征数据集T={(x1,y1),(x2,y2),…,(xn,yn)}其中xi∈Rn，yi∈{0,1},则有如下条件概率分布为logistic回归模型，如式(1)和式(2)，

(1)

(2)

设P(Y=1|X)=π(x)，那么P(Y=0|X)=1-π(x)联合概率分布函数[4]，即似然函数定义为式(3)，

(3)

若想让预测出的结果全部正确的概率最大,根据最大似然估计，就是所有样本预测正确的概率相乘得到的P(总体正确)最大,然而,一个连乘的函数是不好计算的,可以通过两边同时取对数的形式让其变成连加。

取对数似然函数如式(4)，

(4)

对L(w)求极大值，可得到w的估计值，这样就变成了对L(w)为目标函数的最优化问题。在函数最优化的时候习惯让一个函数越小越好,所以在前面加一个负号，得到的就是交叉熵损失函数(cross-entropy loss function)，如式(5)，

P(xi;w))

(5)

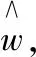
(6)

(7)

将数据集的特征向量xn代入式(6)与式(7)，哪个概率值大就属于哪一类。

2 高斯核支持向量机

支持向量机(Support Vector Machine,SVM)的关键概念可以总结为2点。

(1)在二维上，找一分割线把两类分开；同理，当特征空间是高维时，寻找一平面把特征数据分开，使得离平面最近的样本点具有最大的距离，即超平面，这样数据分类更加准确清晰。实际上超平面的方向和位置完全取决于选择哪些样本点，这些离超平面近的样本点称为“支持向量”。

(2)核函数的作用就是对原始数据进行维度变换，一般是升维变换，原样本空间中线性不可分的样本点在升维之后的空间中变为线性可分的，然后在高维特征空间[5]通过线性超平面进行分类。

常用的核函数有以下4种。

① 线性核：K(x,y)=x·y

③ 高斯核：K(x,y)=exp(-|x-y|/d2)

④ sigmoid核：K(x,y)=tanh(a(x·y)+b)

本文采用的是默认的高斯核函数系数的不同值进行预测癌症分类准确率对比。

高斯核的思想：按一定规律统一改变样本的特征数据得到新的样本，新的样本按新的特征数据能更好地分类，由于新样本的特征数据与原始样本的特征数据呈一定规律的对应关系，因此根据新样本的分布及分类情况，得出原始样本的分类情况。所以高斯核的任务是找到更有利分类任务的新的空间。

高斯核函数的功能步骤[6]如下。

① 先将原始的数据点(x，y)映射为新的样本(x′，y′)；

② 再将新的特征向量点乘(x′，y′)，返回其点乘结果；

③ 计算点积。

假设分类的超平面为wTx+b=0，两个平行的边界超平面分别为式(8)，

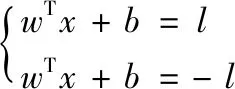
(8)

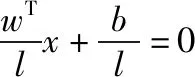
(9)

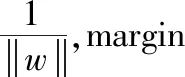
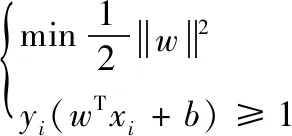
(10)

对于带有约束条件的定义于凸集中的凸函数最小化问题，目标函数是二次函数，约束条件为变量的线性不等式时，常利用拉格朗日对偶性将原始问题转换成对偶问题，下面是凸优化问题构造拉格朗日函数，如式(11)，

(11)

SVM原型和对偶型等价，用过求解拉格朗日对偶问题得到原问题最优解最终结果表示为式(12)，

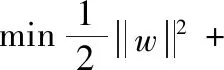
αiαjyiyjxixj

(12)

3 深度学习前馈神经网络

深度学习在医学自主诊断、自然语言处理、生物信息处理等领域都有出色的表现。深度神经网络主要包括前向传播(Forward Propagation,FP)和反向传播(Backward Propagation,BP)[7]两部分。本研究使用的是属于前向传播的多层感知机(Multi-layer Perceptron,MLP)，多层感知机从输入层(Input Layer)到输出层(Output Layer)，上一层的任何一个神经元与下一层的所有神经元都有连接，在经过隐含层的逐层计算后得到预测结果。本研究设定的各层神经元个数以及超参数如表1所示。

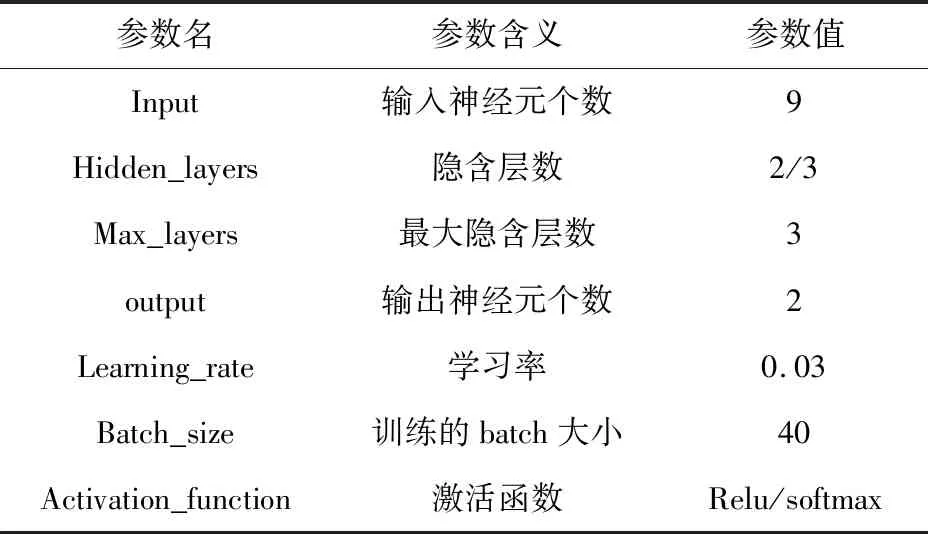
表1 设定参数和参数值

根据数据集特征数量和标签值数量设定输入神经元个数，输出神经元个数是预测的标签值个数。依次实验隐含层数为2层和3层，学习率取值范围0.01-0.05，其中取值为0.03时准确率最高，激活函数Relu用来线性修正，使计算出小于0的值等于0，反之保持不变，同时可以提高训练速度。关于二分类问题先后使用sigmoid函数和softmax函数做了对比，发现softmax函数效果更好。

4 实验

4.1 数据集

本文的实验数据是UCI机器学习库的美国威斯康辛州乳腺肿瘤分类(breast-cancer-wisconsin)数据集，由699条有标记的样本组成，分为良性和恶性两类。该数据集前10个属性为数据特征，最后一个属性为标签数据，如表2所示。

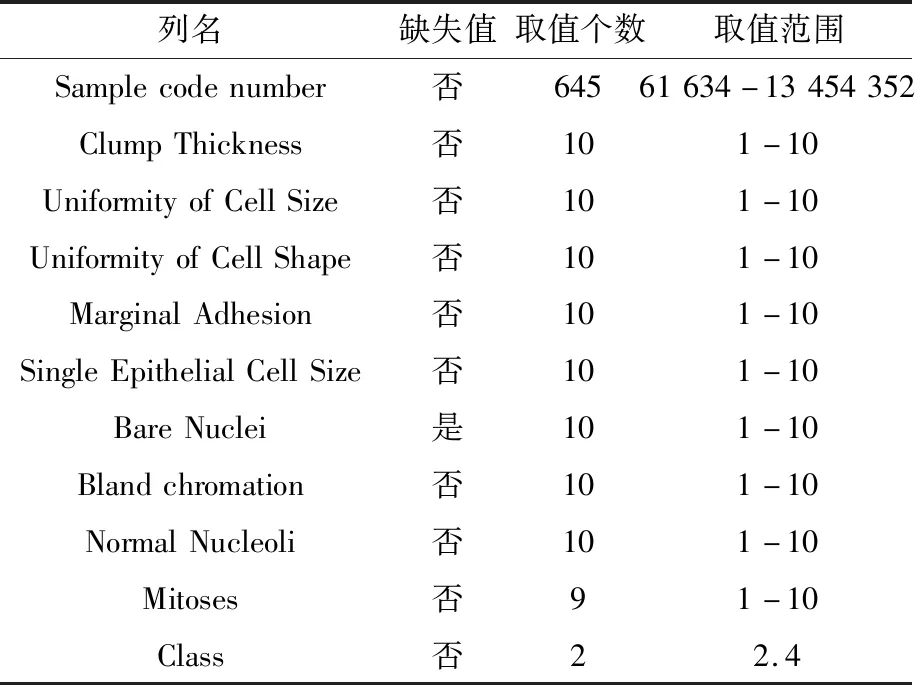
表2 数据集

4.2 数据预处理

(1)缺失值处理：由表2可知“Bare Nuclei”属性存在缺失值，并以“？”的形式出现。这里使Numpy空值替换“？”，再删除空值，这样可以达到删除缺失值的目的。

(2)独热编码(One-hot Encoding)：由于整数特征表示不能在分类器中直接使用，这样的连续输入，估计器会认为类别之间是有序的，但实际却是无序的。创建新的一列，长度等于Class标签值的长度，把新一列全部置为0，如果标签值等于“4”，将把这些对应位置的0，全部替换成1。One-hot达到的效果是把0变为10，1变为01，类似一个数组，使特征数据更加标准化。

(3)特征数据归一化：minmax_scale=preprocessing.MinMaxScaler(feature_range=(0,1))使特征数据变成(0,1)区间的数字，便于预测分析。取训练集525条，其中20%设为验证集，剩下174条作为测试集。

5 三种分类方法的比较

5.1 SVM高斯核不同系数准确率比较

SVM高斯核不同系数准确率比较，如表3所示。

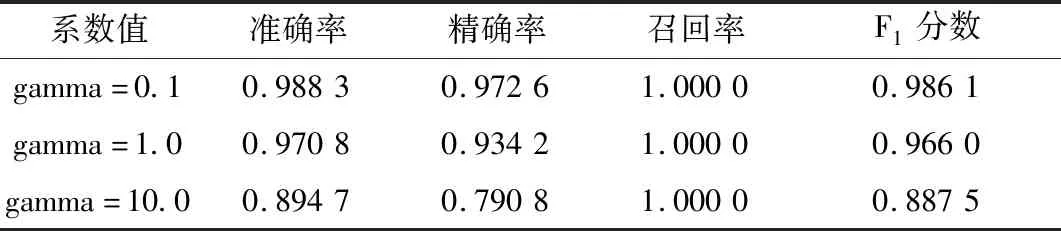
表3 SVM高斯核不同系数准确率比较

由表3可知，gamma=0.1时，准确率最高，模型最优。

5.2 前馈神经网络不同隐含层数下的各项指标比较

前馈神经网络不同隐含层数下的各项指标比较，如表4所示。

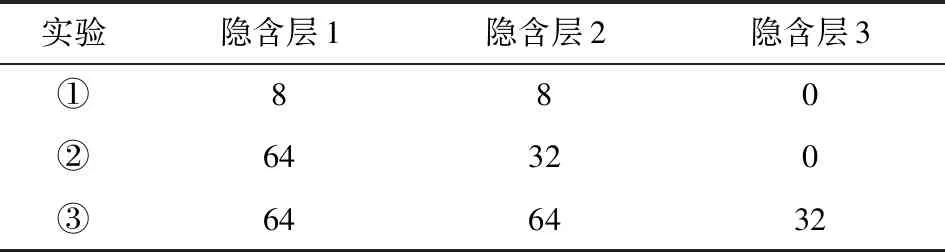
表4 前馈神经网络不同隐含层数下的各项指标比较

训练集和验证集折线图如图1-图6所示。

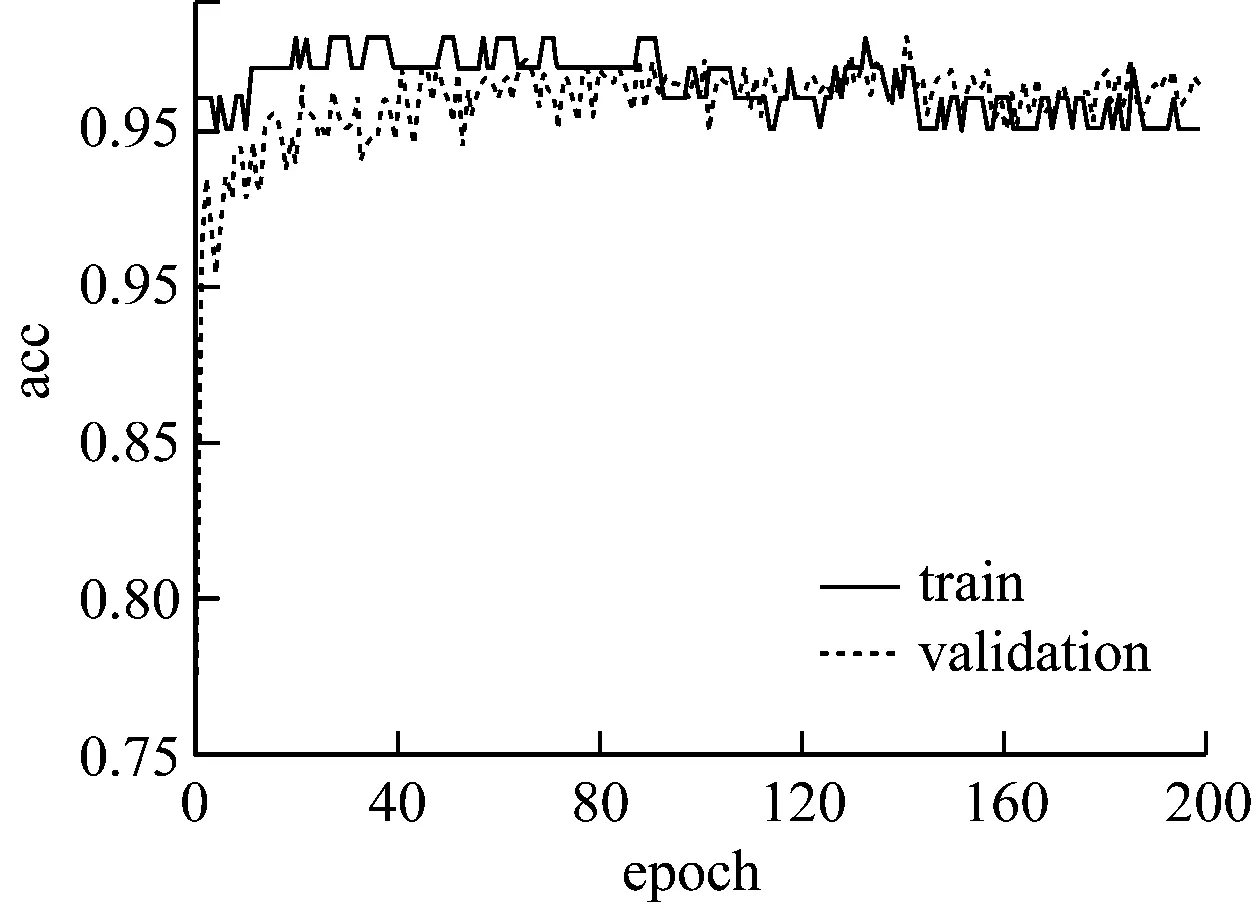
图1 实验①accuracy曲线图

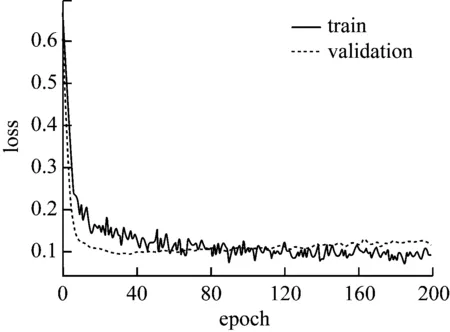
图2 实验①loss曲线图

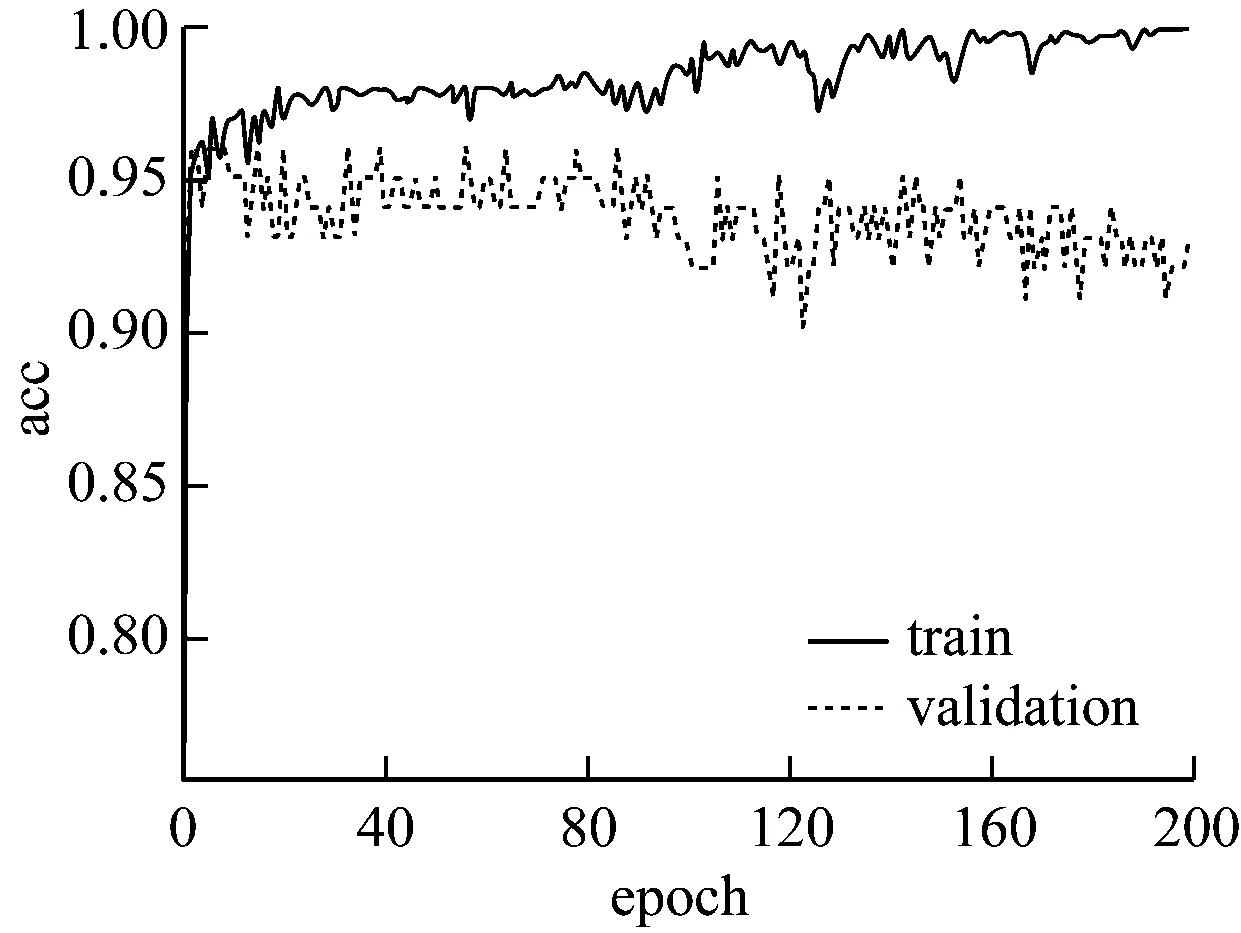
图3 实验②accuracy曲线图

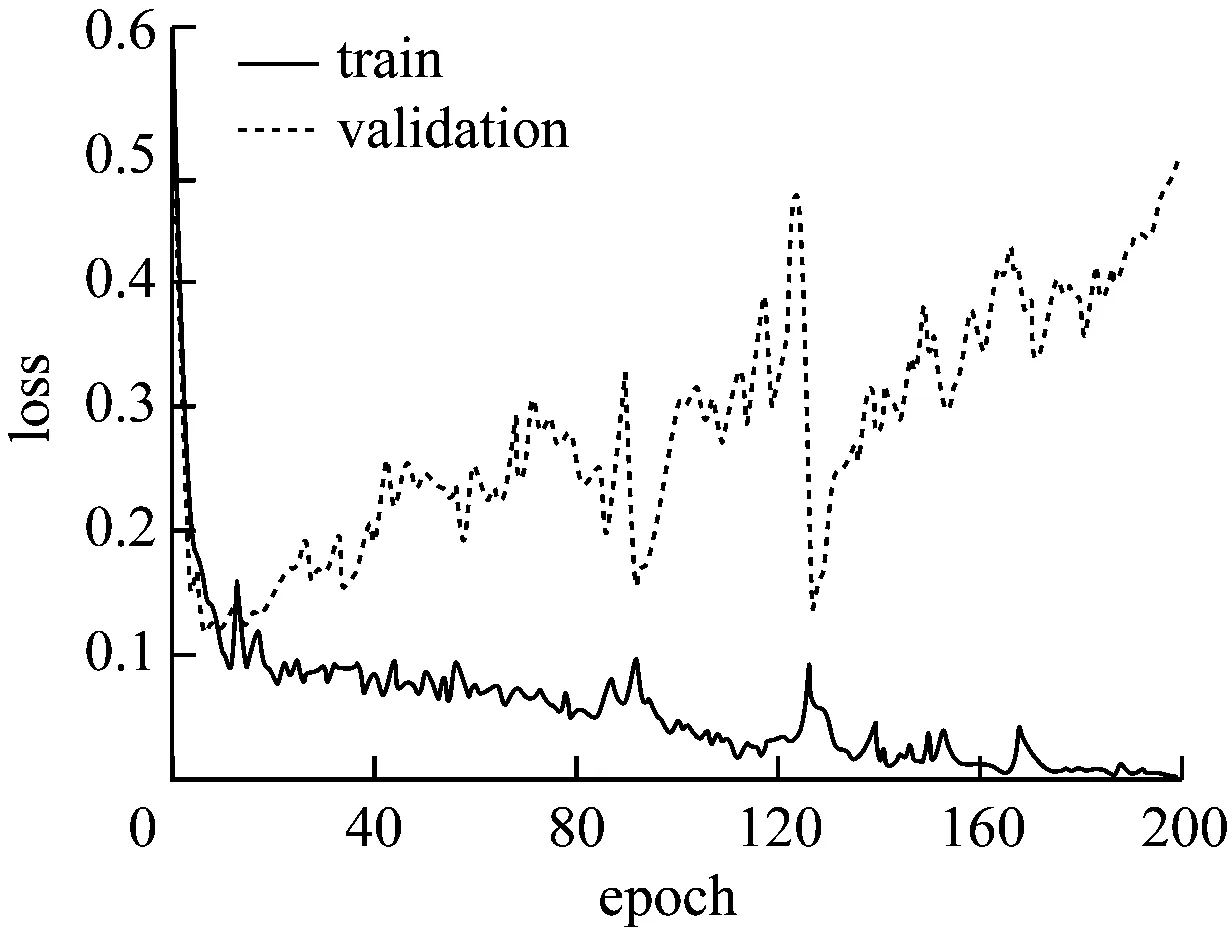
图4 实验②loss曲线图

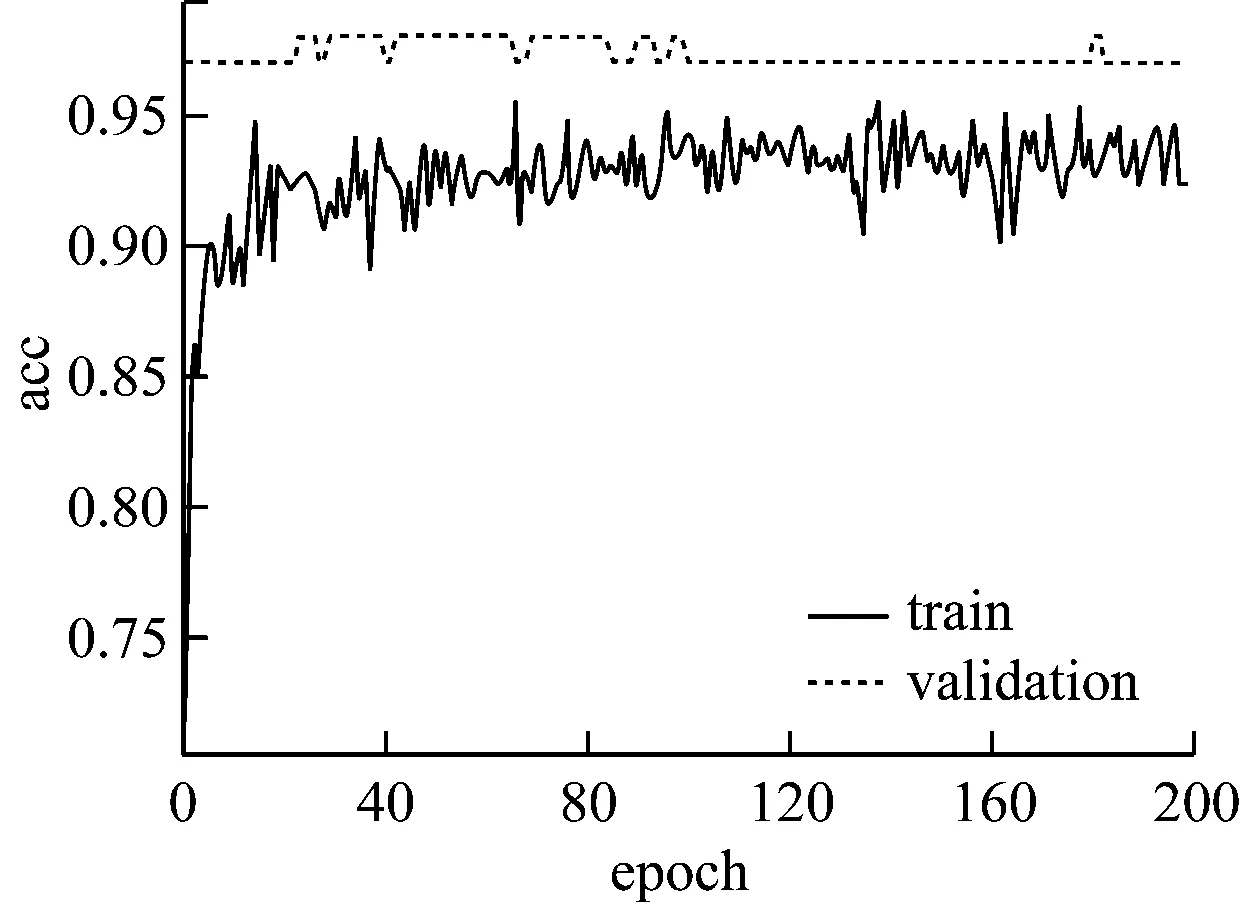
图5 实验③accuracy曲线图

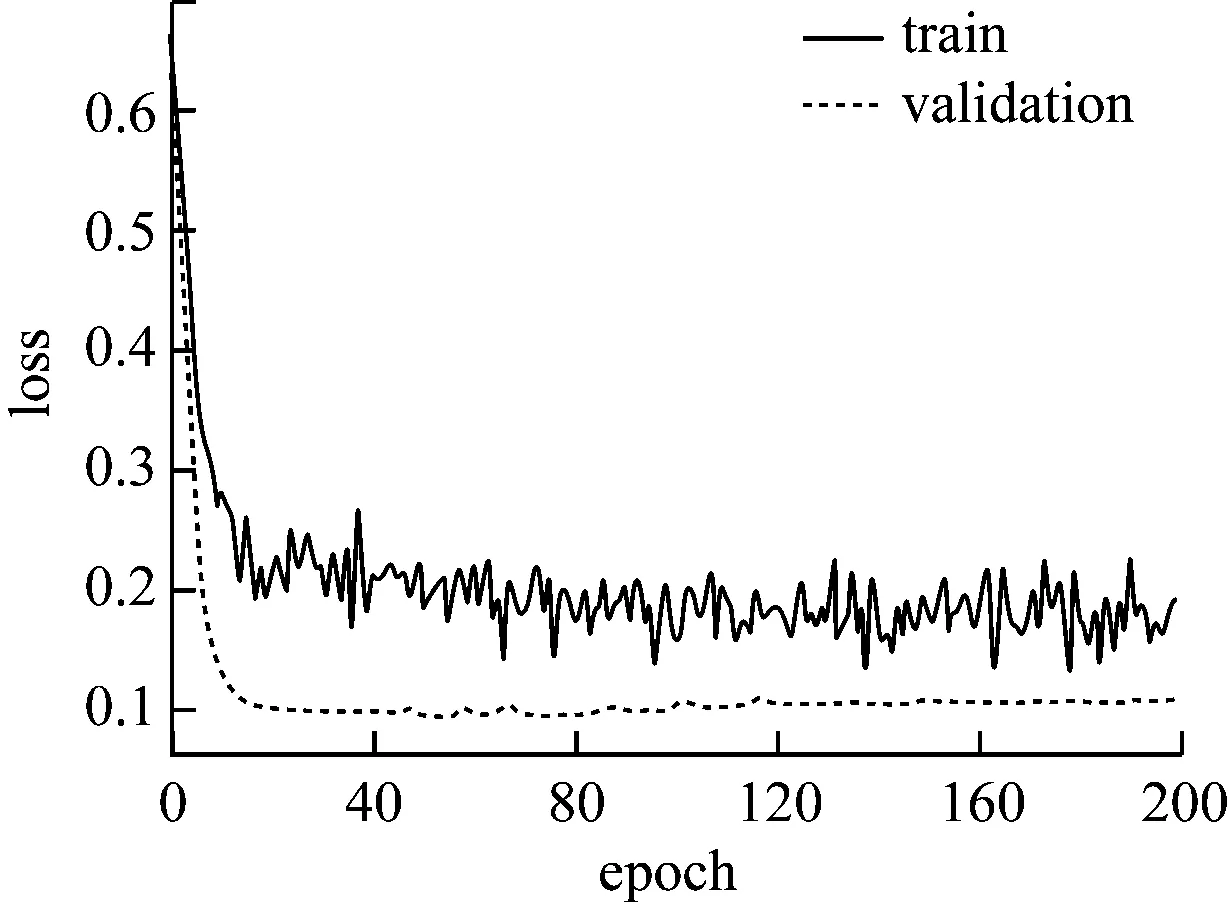
图6 实验③loss曲线图

可以看出，隐含层神经元个数增加为64时开始出现过拟合现象，增加相应比例的层数和神经元个数，过拟合现象逐渐严重，采用dropout正则化可以适当解决这一现象，设置丢弃神经元概率值0.5,最终结果如图7、图8所示。

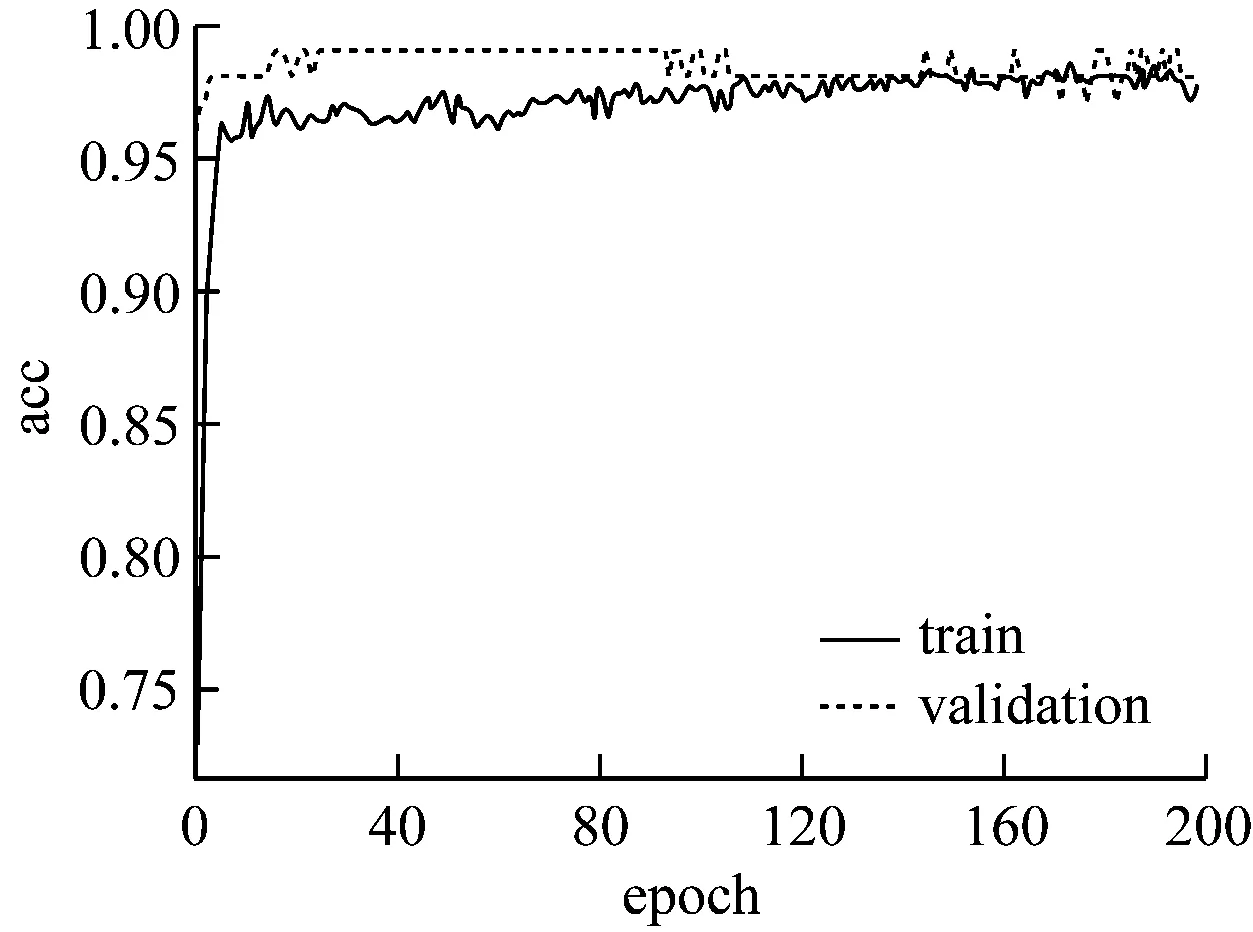
图7 dropout后实验②accuracy曲线图

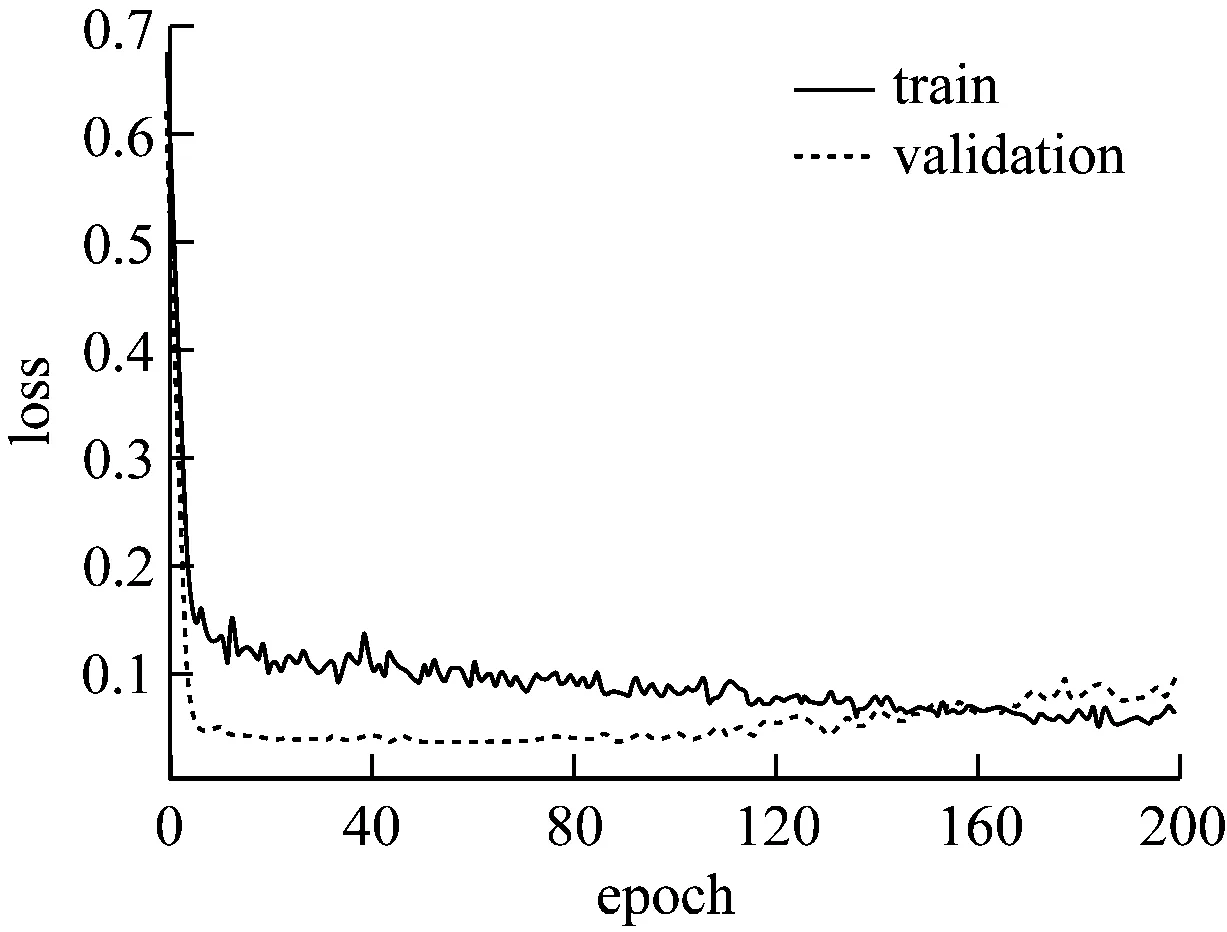
图8 dropout后实验②loss曲线图

在神经网络预测患病准确率即准确程度，即预测正确数量和总样本数量比值，准确率计算用式(13)，

(13)

在神经网络预测患病召回率方面，召回率即正确预测为真正患病数量与真正病例总数的比值，因此召回率计算用式(14)，

(14)

在神经网络预测患病漏报率方面，漏报率即本为恶性肿瘤的患者数据被分类为良性肿瘤，因此漏报率计算用式(15)。

(15)

其中TP指将正类预测为正类数，称为真正例；FP指将负类预测为正类数称为伪正例；TN指将负类预测为负类数，称为真反例；FN指将正类预测为负类数，称为伪反例。

5.3 三种分类方法比较

使用测试集来评估各模型最终的泛化能力，如表5所示。

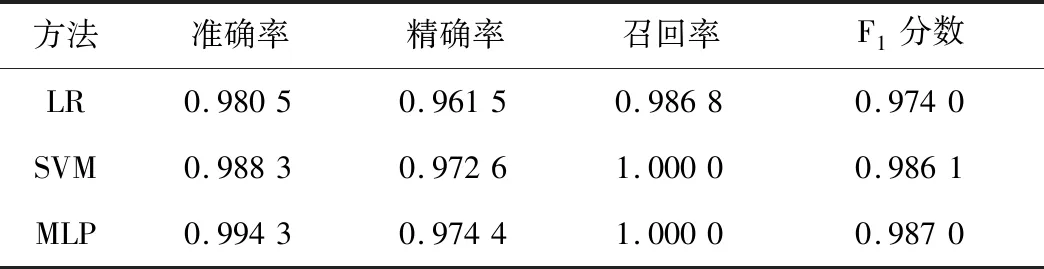
表5 3种模型各项指标比较

6 基于SVM优化的前馈神经网络

上述logistic、SVM、MLP在同一乳腺癌数据集的各项指标比较，由于数据集数量较少，所以神经网络的优势并没有完全凸显出来，计算每个模型的迭代时间，在准确率可以保证在98%以上的情况下迭代的时间由小到大排序为SVM、logistic、MLP，由此可见神经网络在准确率方面没有传统SVM模型高，且运行速度慢，所以提出一种基于SVM的前馈神经网络(SVM-MLP)，基本思想为利用SVM分类好的乳腺癌数据，重新使用前馈神经网络进行检测分类，这样可以在保证准确率和召回率的情况下一定程度上减少神经网络的迭代时间。

使用np.concatenate()实现对应行的数组进行拼接，使用pd.DataFrame()提供有序的列和不同类型的列值，将SVM分类好的原数据生成CSV表格，由于SVM分类出的数据恶性占比大，直接放入神经网络中会出现数据分析不平衡状况，为了保持数据平衡，逐渐增加成比例的良性数据完成神经网络的预测模型。实验结果表明加入50条良性数据时，准确率最高可达到99.1%，随着数据分布愈加平衡，准确率也会相应上升。4种分类方法准确率、迭代时间比较结果如表6所示。

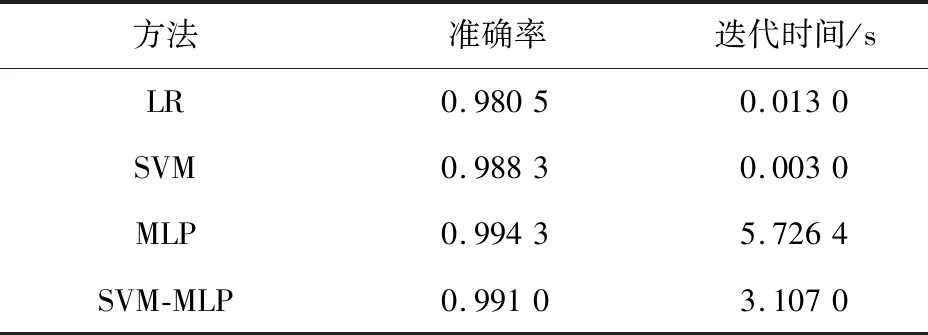
表6 4种分类模型在准确率、迭代时间上比较

在文献[8]中，提出基于重构误差的深度信念网络深度自适应确定算法，基本思想是由多个受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)组成的深度置信网络(Deep Belief Networks,DBN)在训练过程中自适应确定隐藏层深度，并且在阈值有偏差的情况下仍能有一个较好的网络模型深度，最大隐含层数是7，每层神经元个数为32，测出的最高准确率为95.43%，虽然可以自主确定模型深度，但是准确率较低。在文献[9]中，提到的BP神经网络向后传播误差，隐含层数为1，在达到最高准确率98.9%时的隐含层节点数是6。基于SVM优化后的前馈神经网络与其他模型比较结果如表7所示。

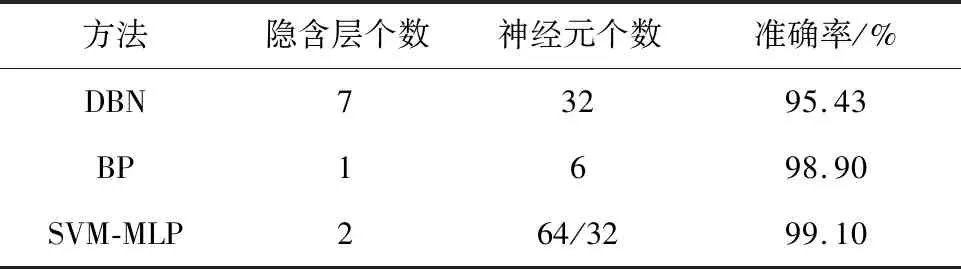
表7 基于SVM优化后的前馈神经网络与其他模型的比较

7 总结

本研究是在美国威斯康辛州乳腺肿瘤分类数据集上分别使用了LR、SVM、MLP 3种模型，取得了98.0%、98.8%、99.4%的准确率，2%、0%、0%的漏报率。分析了2个机器学习领域的算法和深度学习神经网络在该分类问题上的比较结果。

为缓解前馈神经网络对于这一乳腺癌数据集迭代时间漫长，提出一种利用SVM分类好的数据再次放入前馈神经网络的预测模型，相比前馈神经网络减少了近一半的迭代时间，且准确率比传统SVM模型要高，最高准确率可达到99.1%。本次实验数据量比较少，为了能让神经网络训练达到更好的效果，需要继续应用更有代表性的医学样本数据，在网络结构复杂性方面也应有更进一步的研究。