表征绕组特征的参数与绕组变形关系的仿真

姜毅， 严娜， 江晓波

(云南电网有限责任公司，昭通供电局，云南，昭通 657000)

0 引言

变压器是电力系统内重要的电气设备，变压器可实现电力系统内不同电压等级、电网功率的互联和交换，电力系统安全稳定性受变压器直接影响[1]。电力系统规模不断提升令电力系统电压等级有所提升，电力系统容量趋于最大化，系统内电力结构复杂，电力系统内变压器出现故障将影响全部电力网络正常运行，变压器检修难度较高将为电力系统以及人类生活带来极大影响。

近年来大量研究学者研究绕组变形的诊断方法，短路阻抗法、低压脉冲法等均为常应用于判别绕组变形的重要方法，变压器阻抗以及短路阻抗内的绕组位置以及几何尺寸直接影响电感分量[2]，变压器绕组状态利用变压器短路电抗变化判别已成为众多研究学者重视的问题，通过以上方法虽然可以判别变压器内的绕组问题，但无法量化变压器绕组的变形程度，高效的、定量的变压器绕组变形判别方法已成为目前急需解决的问题。在线判别和离线判别变压器绕组变形是目前常用的2种判别方法。离线判别具有成本高、判别过程复杂以及耗时较长的缺陷，且离线判别需要停电作业对周围用电产生较大影响。在线判别具有高效、经济的优势，且不影响电力系统正常运行，因此利用在线方式判别变压器绕组变形已成为电力系统发展的重要趋势。

由于绕组变形造成变压器内部匝间故障是目前导致变压器事故的重要因素，研究表征绕组特征的参数与绕组变形关系的仿真方法，可有效判断变压器是否发生绕组变形故障。目前很多学者对在线方式判别变压器绕组变形进行了研究。比如邹林等[3]基于等值电路参数利用电路仿真软件PSPICE仿真绕组变形下的频率响应特性曲线,得到了3种变形类型对谐振点的频率、幅值的影响，为该领域做出了一定贡献；张重远等[4]研究了频率响应法诊断变压器绕组径向变形的仿真和实例，证明了绕组的径向变形会导致频率响应曲线上谐振点的频率和幅值发生变化，具有一定的实用价值；江俊飞等[5]对自耦变压器分裂式绕组频率响应分析建模与故障绕组识别进行了研究，并提出了分裂式绕组发生轴向移位故障时快速识别故障绕组的判断方法，有效提高了识别故障绕组的效率。工程计算法可计算变压器内部规则绕组漏磁场分布，但误差较高[6]，无法实现变压器内部绕组变形精准判别。设所建立变压器模型具有相同的高压绕组以及低压绕组[7]，高压绕组与低压绕组分别分布于模型外侧以及内侧，变压器绕组上均匀分布着绕组电流。所建立的模型利用中心轴为铁芯的同心圆柱体表示高压绕组以及低压绕组[8]。

因此，本研究利用有限元方法建立表征绕组特征的参数与绕组变形关系的双绕组、同芯式变压器漏磁场模型，通过二维泊松方程混合边值的有限元解分析变压器绕组漏磁场，利用最小二乘算法基于所建立变压器漏磁场模型辨识可表征绕组特征的漏电感参数，通过所获取漏电感值与实际漏电感值相比实现变压器绕组变形判别。通过有限元方法建立变压器绕组仿真模型并分析表征绕组特征的参数与绕组变形关系，仿真结果可知，该方法可有效辨识表征绕组特征的漏电感参数，依据表征绕组特征参数与绕组变形关系实现变压器高压与低压绕组变形的精准判别，判别精度高达99%以上，验证利用表征绕组特征的漏电感参数在线监测绕组变形可行性。

1 表征绕组特征的参数与绕组变形关系

1.1 建立变压器漏磁场模型

变压器漏磁场分布与尺寸极为重要，变压器线圈的附加损耗、感抗以及内部金属结构元件耗损均由漏磁场分布与尺寸决定[9]，故障状态下和正常运行时电磁力对线圈的作用同样需要通过漏磁场分布与尺寸决定。

利用二维准泊松方程混合边值的有限元解计算变压器绕组漏磁场。用μFe=∞与空气磁导率μ=μ0分别表示铁芯内磁导率以及绕组和求解区域内磁导率，绕组内与绕组外电流密度分别为J以及0。

所建立模型计算区域以及待求解磁场分别存在流载体以及旋度场[10]，求解变量选取向量磁位Fz。磁力线与模型的铁芯表面为垂直关系，此时需满足∂Fz/∂n=0，即向量磁位的法向量为0。

设所建立模型变压器属于芯式变压器，变压器内两相绕组间隙处向量磁位Fz为常数，本研究将其取为0。变压器模型向量磁位所符合泊松分布以及边界条件如式(1)，

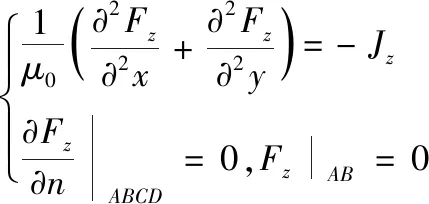
(1)

利用有限元方法获取式(1)的向量磁位值。

利用体积增量为截面积的圆环形空间的计算单元作为面积增量[11]，设置变压器模型轴线为计算中心，获取计算空间内磁场能量，将所获取能量在(0,Lw}范围内积分，获取全部漏磁场空间的磁场能量如式(2)，

(2)

式中，Ck与xk分别表示第k个面积增量dx内磁感应强度平均值以及横坐标值，Dc表示变压器模型的铁芯柱直径，Lh表示高压层电感。

高低压侧漏电感不平衡度Lu如式(3)，

(3)

式(3)利用变压器铁芯及绕组结构可确定漏电感不平衡度值，Lσl表示变压器模型高压层漏电感，Lσh表示变压器模型低压层漏电感。所建立变压器模型绕组为对称状态时，高低压侧漏电感不平衡度为1。

1.2 漏电感参数与绕组变形关系

利用最小二乘算法辨识可表征绕组特征的漏电感参数，最小二乘法是依据误差平方和作为准则获取最优参数的高效方法[12]。设y与H分别表示数据向量以及数据矩阵，大小分别为k×1以及k×l，通过最小二乘算法求解矩阵方程H(x}=y时，用l表示未知数数量，所获取矩阵H的秩等于以及小于l时，方程分别存在唯一解以及通过众多解可获取同样H(x}值，此时未知参数分别为可辨识以及不可辨识。

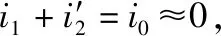
(4)

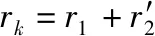
用xk表示厂家提供的短路电抗，角频率为ω，绕组等值漏电感值获取如式(5)，

(5)

漏电感值在原、副边绕组变形时形成变化[14]，依据式(4)将辨识所获取漏电感值与实际漏电感值相比，即可判别变压器绕组变形情况。

在变压器正常运行情况下电压电流仅包含工频信号为50 Hz的单一数据，采用单一工频信号建立的数据矩阵H的秩为2。利用式(4)所获取参数辨识矩阵方程仅可辨识独立参数数量为2，离散化处理式(4)，用ΔT表示两点间采样间隔距离，可得式(6)，

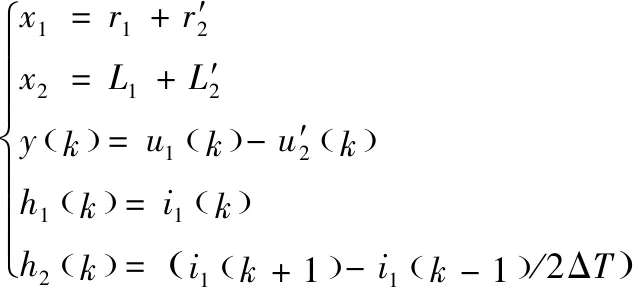
(6)

此时式(4)可转化为下列的式(7)，

y(k}=x1h1(k}+x2h2(k}

(7)

通过最小二乘算法获取最优x1、x2，可得x1、x2二次函数如式(8)，

(8)

式中，m表示获取估计参数所需数据点数量，式(8)成立条件为式(9)，

∂E2/∂xi=0，i=1,2

(9)

可得待辨识参数如下：

(10)

式(10)需符合条件式(11)，

(11)

将以上方程组利用连续采样点数量m求解，利用最小二乘算法获取x1、x2的参数估计值。将最小二乘算法应用于漏电感参数辨识中可充分表征绕组特征[15]，降低由于采样及计算误差对参数辨识造成的波动，依据表征绕组特征的漏电感参数与绕组变形关系实现绕组变形的判别。

2 仿真研究

2.1 有限元仿真模拟

为验证本研究表征绕组特征的参数与绕组变形关系有效性，采用有限元软件模拟本研究所建立变压器漏磁场模型进行仿真实验。采用d11接法作为变压器的联结方式，所设计的仿真变压器绕组布置如图1所示。

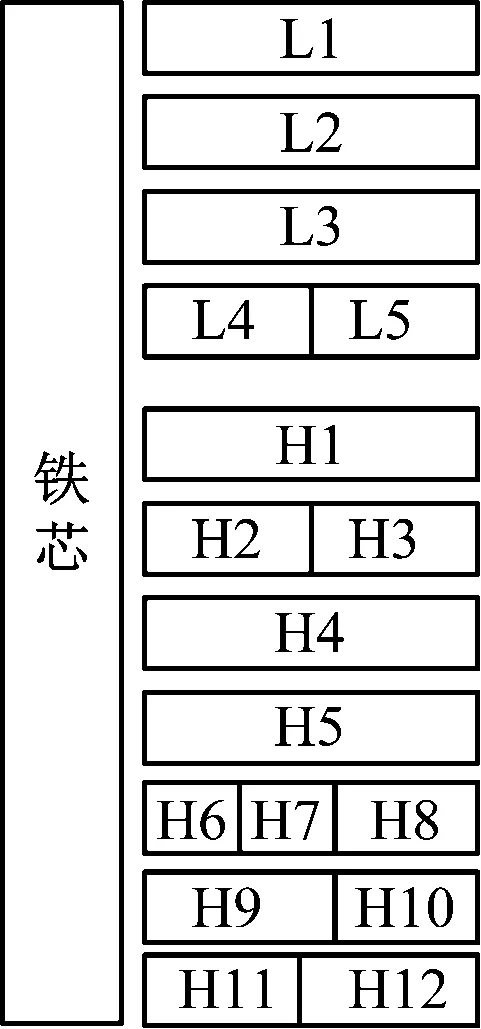
图1 变压器绕组布置

所设计的仿真变压器为双绕组、同芯式变压器组，模拟变压器铁芯设置为回型结构，高低压绕组布置与绕制方式分别为上下布置以及连续式布置。

低压绕组内径与外径分别为120 mm以及295 mm，高度为110 mm，布置方式为上下布置。低压绕组内包括11个匝数为8的线饼；高压绕组内径与外径分别为120 mm以及325 mm，高度为118 mm，高压绕组内包括12个匝数为32的线饼；存在众多抽头于高低压绕组内，设置低压绕组以及高压绕组数量分别为5个以及12个。高压绕组与低压绕组分别为L1-L5以及H1-H12，高低压子绕组匝数见表1。

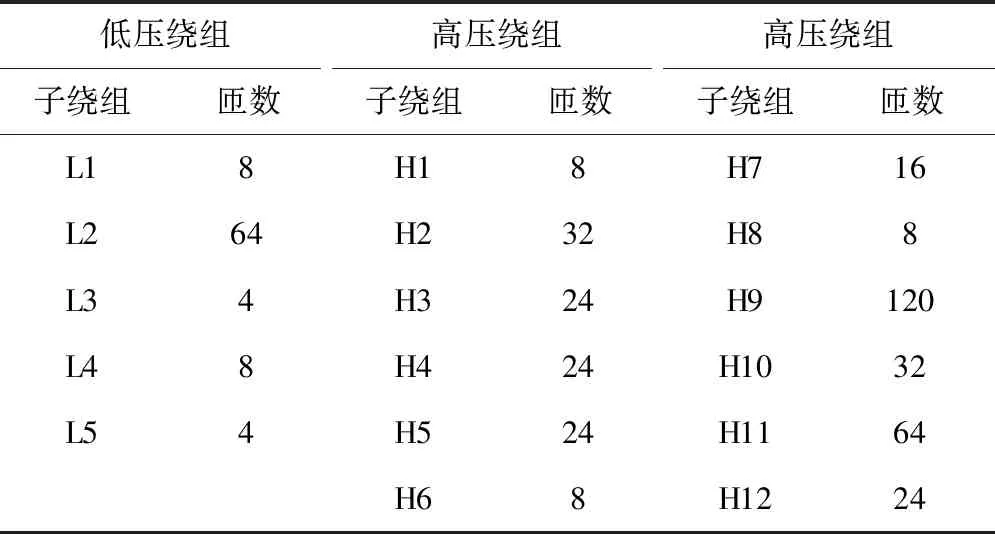
表1 子绕组与匝数

原副边绕组的匝数、相对位置受子绕组不同连接状况影响。

仿真实验接线过程中，低压绕组与高压绕组分别由L1、L2、L3以及H2、H3、H6、H7、H9、H10、H11共同组成自绕组数量为76匝以及296匝。

假设单项变压器额定电压以及额定容量分别为95 V/220 V以及2 kVA，采样速率为每周波110点，A/D转换精度为12位，选取两个周波数据作为仿真实验参数辨识以及绕组变形判别。

2.2 变压器绕组参数辨别

采用本研究参数辨识方法实现变压器漏感参数辨识。通过空载合闸实验检测不同合闸角情况下原方绕组电阻以及副方绕组电阻辨识精度。参数辨识结果见表2。

由表2仿真结果可以看出，本研究所提方法所用参数辨识算法具有较高的辨识精度，不同角度时辨识误差均保持在允许范围内，说明本研究所提方法具有较高的辨识精度。利用辨识算法电阻输出值的三相绕组电阻平均值作为仿真模型电阻值，可有效降低绕组变形判别误差。本研究所提方法在变压器绕组电流与端口电压呈正弦量情况下可保持较高的辨识精度，具有较高的辨识性能。

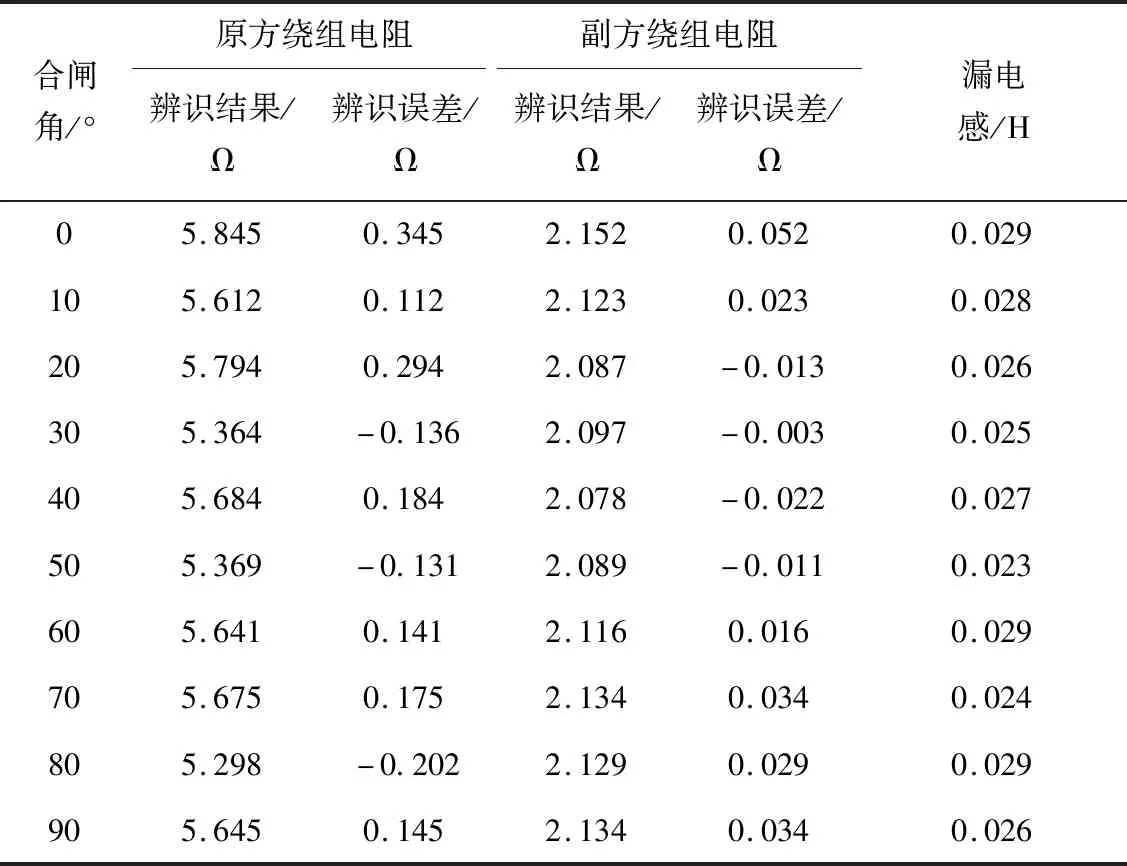
表2 变压器绕组参数辨别

2.3 变压器绕组变形判别

为验证本研究所提方法利用表征绕组特征的漏电感参数与绕组变形关系实现变压器绕组变形的可行性，设计本研究所提方法依据绕组参数与绕组变形间关系，利用参数辨识结果判别变压器低压、高压两组绕组变形实验，判别结果表明本研究所提方法可有效判别低压变短缺角、低压单端变短、低压双端变短、低压绕组缺角、高压变短缺角、高压单端变短、高压双端变短、高压绕组缺角8种不同变形情况。

本研究所提方法利用参数辨识结果判别变压器低压绕组变形结果如表3所示。

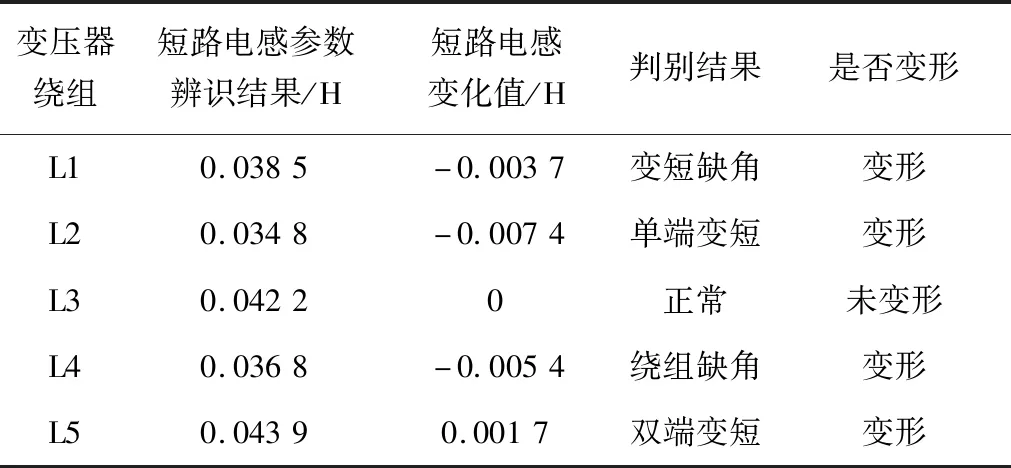
表3 变压器低压绕组变形判别结果

利用参数辨识结果判别变压器高压绕组变形结果如表4所示。

表4 变压器高压绕组变形判别结果

综合表3、表4判别结果，统计采用本研究所提方法判别不同变形情况的判别精度，统计结果如图2。

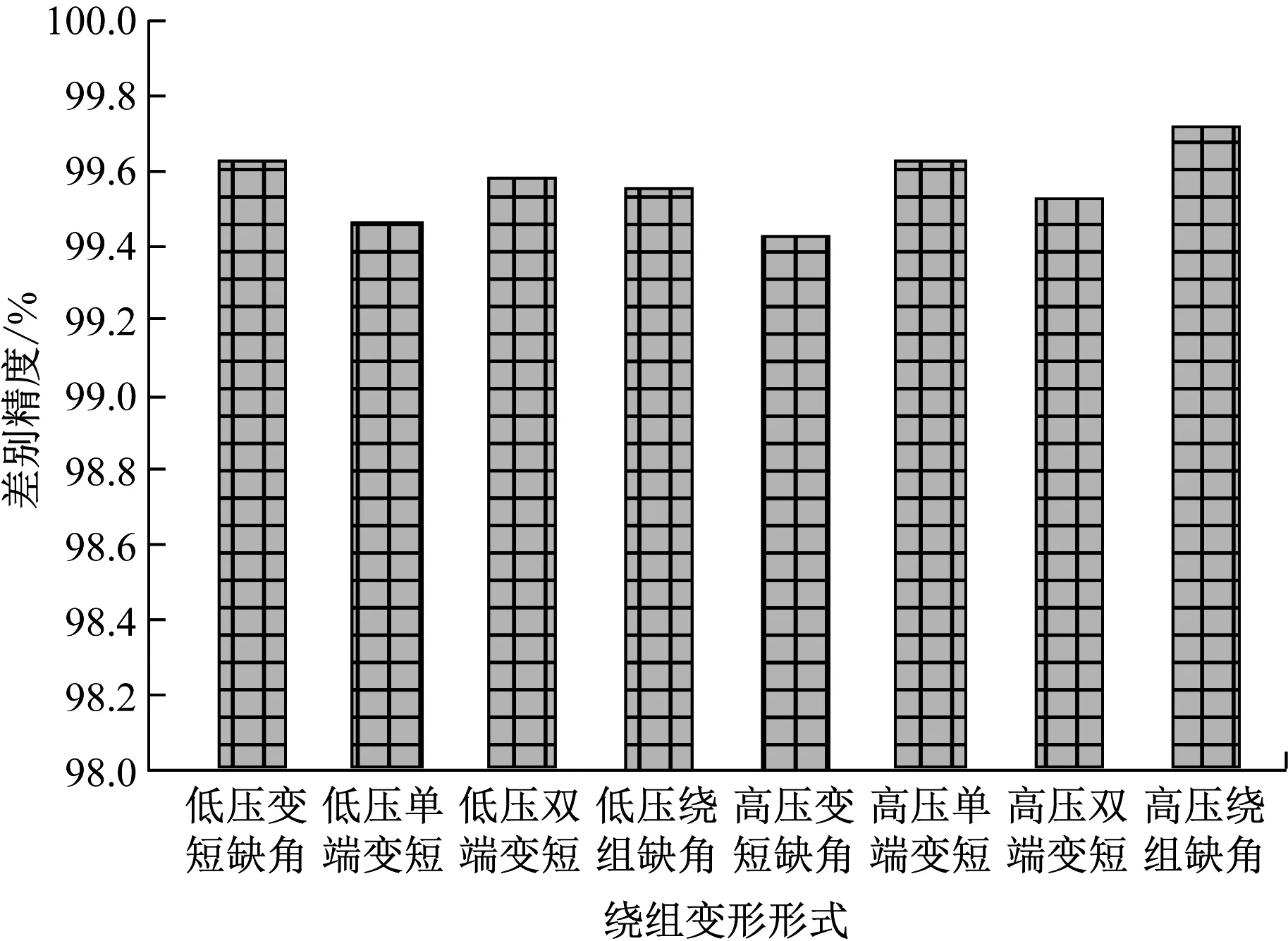
图2 不同变形情况下判别精度

由图2可以看出，本研究所提方法具有较高的判别精度，可精准判别不同形式的绕组变形，不同变形情况下判别精度均高于99%。本研究所提方法可有效定位绕组变形为高压侧绕组以及低压侧绕组，具有较高的判别性能。

仿真模拟结果有效地验证绕组变形与表征绕组特征参数具有较高的关联程度，采用最小二乘算法的参数辨识方法可精准辨识由于绕组变形造成的漏电感值，依据漏电感值变化量与绕组变形程度精准判别绕组变形情况。本研究所提方法判别绕组变形精度可高达99%以上，有效验证该方法具有较高的判别性能。

3 总结

为提升变压器绕组变形判别精度，研究表征绕组特征的参数与绕组变形关系的仿真方法。利用有限元方法建立表征绕组特征的参数与绕组变形关系的双绕组、同芯式变压器漏磁场模型，通过二维泊松方程混合边值的有限元解分析变压器绕组漏磁场，利用最小二乘算法基于所建立变压器漏磁场模型辨识可表征绕组特征的漏电感参数，通过所获取漏电感值与实际漏电感值相比实现变压器绕组变形判别。通过有限元方法建立变压器绕组仿真模型并分析表征绕组特征的参数与绕组变形关系，仿真结果可知，该方法可有效辨识表征绕组特征的漏电感参数，依据表征绕组特征参数与绕组变形关系实现变压器高压与低压绕组变形的精准判别，判别精度高达99%以上，验证利用表征绕组特征的漏电感参数在线监测绕组变形可行性，因此该方法可应用于实际电力系统绕组变形在线监测中。该方法目前仅验证了表征绕组特征的漏电感参数在线监测绕组变形可行性，但电力系统中绕组变形不仅只由单个原因造成，关于电力系统中绕组存在的问题今后还有待进一步研究。