沪深300指数波动率和VaR预测研究——基于投资者情绪的HAR-RV GAS模型

沈银芳，严鑫

（浙江财经大学数据科学学院，浙江 杭州 310018）

0 引言

随着经济全球化和金融自由化进程的不断推进，如何有效管控金融风险成为亟待解决的重要问题。准确度量金融资产收益率的尾部风险值（value at risk，VaR）是目前业界广泛使用的风险管理工具之一[1]。如何精确估计和预测金融资产的波动率是VaR预测的核心。数据驱动波动率模型的一般框架为CREAL等[2]提出的广义自回归得分（generalized autoregressive score，GAS）模型，该模型具有较强的灵活性，具有观测驱动模型的优点和较强的数据模型适应性，还能充分利用完整的密度结构实时驱动时变参数。GAS模型一经提出，便广受关注，被应用于众多领域，尤其在波动率和VaR预测方面效果优良。王天一等[3]提出的已实现GAS-GARCH模型较已实现广义自回归条件异方差（realized GARCH）模型具有更优的VaR预测能力。沈根祥等［4］提出的基于高频数据的得分驱动厚尾分布波动率（GAS-HEAVY）模型，通过模拟和实证分析发现，该模型的数据拟合和波动率预测效果较同类模型更优。NANI等［5］融合了GAS、最小二乘支持向量回归（LS-SVR）和固定大小最小二乘支持高量回归（FS-LS-SVR）预测条件VaR的半参数方法，改善了VaR性能。PATTON等［6］基于GAS模型，提出了一种动态VaR和预期损失（ES）的联合估计和预测框架，ES-VaR模型优于基于GARCH或滚动窗口的预测模型。宋加山等［7］基于沪深300成分股36家上市公司数据，构建了GAS-混合Copula模型，用于度量边际期望损失（MES），以此分析不同行业的系统性风险。综上可知，GAS模型对波动率和VaR有优良的预测效果，同时发现，在GAS模型的相关理论和应用研究中，较少考虑已实现波动率和投资者情绪的影响以及波动率的长记忆性。

事实上，随着（超）高频数据的出现，ANDERSEN等［8］提 出 了 一 类 度 量 波 动 率 的 新 方法，即已实现波动率，该方法不需要模型假设，计算简单方便，且在一定条件下可实现对真实波动率的无偏估计。近年来，基于高频数据的已实现预测方法在波动率和风险度量研究中的重要性越来越显著，如何将已实现波动率纳入传统波动率和风险度量模型成为学者普遍关心的问题。邵锡栋等［9］基于沪深指数的日内高频数据，得到已实现波动率和已实现极差模型的预测能力强于传统GARCH族模型。文献［10-11］指出，在波动率模型中加入已实现波动率的方法有很多优势。王春峰等［12］指出，基于日内高频收益的SKST-RS模型的VaR预测能力强于SKST-RV模型和基于日间收益率的GARCH模型。刘晓倩等[13]以沪深300指数为研究对象，发现基于高频数据的HAR模型的波动率刻画预测能力优于低频传统GARCH模型和随机波动率（stochastic volatility，SV）模型。于孝建等[14]基于沪深300指数混频数据，对混频已实现GARCH模型的波动率和VaR预测效果进行了对比研究。陈声利等[15]认为，高频波动率比低频波动率蕴含更多信息，且计算效率更高，采用高频波动率建立高效的尾部风险测量方法将成为研究趋势。

另外，随着行为金融学的兴起，普遍认为金融市场的收益率及其波动性受投资者情绪影响。BAKER等[16]选取有关代理变量，构建投资者情绪指标，分析投资者情绪对股票收益的影响。SEO等[17]研究了投资者情绪对期权隐含信息波动性预测能力的影响。DEBASISH等[18]以印度股票市场为背景，研究了投资者情绪与股票收益率波动的关系，投资者情绪在短期和中期均会影响条件波动和已实现波动。SCHNELLER等[19]认为，德国和欧洲投资者情绪对本地股市的收益率波动性很重要。还有少量文献讨论投资者情绪对金融风险的影响。佟孟华等[20]采用CoVaR方法度量了我国上市金融机构的系统性风险，结果表明，投资者情绪对未来的系统性风险有显著的正向影响。目前，鲜有文献将投资者情绪作为影响因子加入波动率模型进行VaR预测效果评估。

与此同时，金融市场具有长记忆性，且获得广泛认同，这对于金融风险管控十分重要，因为一旦忽略金融市场的长记忆性特征，金融市场的风险控制、趋势掌控与资产定价等均会受影响。CORSI[21]提出了基于异质市场假说的已实现波动率异质自回归（heterogeneous autoregressive of realized volatility，HAR-RV）模型，其对于不同周期波动率非对称传导引起的波动率序列持续相关关系的捕捉非常灵敏，对于金融时间序列中的长记性、厚尾等特征的刻画能力较强。HUANG等[22]在已实现GARCH模型中嵌入HAR-RV，建立了已实现HAR GARCH模型，在一定程度上对市场波动的长记忆特征具有刻画作用。YANG等[23]运用HAR模型预测了原油期货市场的波动性，发现当考虑了投资者情绪和杠杆效应时，模型样本内拟合和样本外预测的性能更优。

沪深300指数覆盖了沪深市场50%以上的市值，可在一定程度上反映沪深2个市场的整体走势。研究沪深300指数的波动率特点、准确预测波动率趋势和VaR，对投资者和市场均很重要。受HUANG等[22]，YANG等[23]研 究 的 启 发，基 于HAR和GAS模型的已有研究成果，尤其是在波动率预测方面的诸多方法和结论，本文以沪深300指数5 min和日收益率为研究对象，在沪深300指数收益率和已实现波动率具有长记忆性的事实基础上，将HAR-RV和GAS模型相结合，以期充分利用由高频数据计算的已实现波动率，提高对波动率的预测能力。为更准确地预测波动率和VaR，纳入了投资者情绪指数，设定得分驱动波动率更新项，构建时变波动率HAR-RV和HAR-RV-SENT GAS模型。利用自相关函数和SPA检验[24]等方法比较波动率模型的样本内拟合和样本外预测能力。鉴于波动率研究的金融风险管理应用，将加入已实现波动率和投资者情绪的GAS模型与基础GAS模型进行比较，分析其VaR预测效果。

本文将GAS模型与经典的HAR-RV模型相结合，纳入投资者情绪指数，构建GAS波动率模型，预测沪深300指数波动率和VaR，为GAS模型的应用研究开辟了新方向，同时为波动率和金融资产尾部风险度量提供了更优的计量方法，对资产配置和风险控制具有借鉴意义。

1 理论模型

1.1 GAS波动率模型

假设金融资产日收益率rt的密度函数为p(rt|σ2t，Ft；θ)，Ft为t日的可用信息集，θ为静态参数向量，波动率参数σ2t具有时变演化形式：

其中，ω，Ai，Bj为系数矩阵，由θ确定，即

式（1）～式（3）给出了阶数为p，q的GAS波动率模型，记为GAS（p，q）。当St为单位矩阵且p=q=1时，标准化GAS（1，1）模型即为基础GAS模型。

1.2 HAR-RV（-SENT）GAS波动率模型

为在一定程度上提高波动率和VaR预测精度，将投资者情绪指数纳入HAR-RV结构，得到HARRV-SENT模 型。HAR-RV模 型 为

HAR-RV-SENT模型为

其中，ωt+1的均值为零且独立同分布，分别为日、周、月频率的已实现波动率，、、分别表示日、周、月频率的投资者情绪指数。计算式为：

为充分保留市场的长期相关性和投资者情绪，剖析投资者情绪和已实现波动率对条件波动率和VaR预测的影响，分别将HAR-RV、HAR-RVSENT与GAS（p，q）模型相结合，构造数据驱动广义自回归得分波动率模型，分别记为HAR-RV GAS（p，q，r）和HAR-RV-SENT GAS（p，q，r）。模型扩展定义如下：

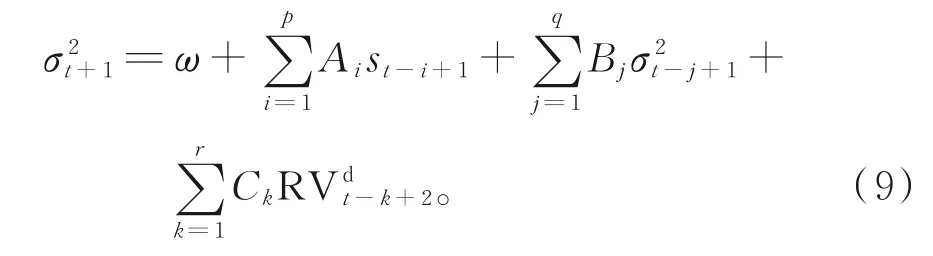
模型的具体假设条件与GAS模型一致。GAS（1，1）模型较简约且在GAS族中具有典型代表性，故取p=q=r=1，这并不影响本文的一般性。

2 实证分析

2.1 实证数据及描述性统计分析

选取沪深300成分股市场展开研究，数据区间为2016年8月23日—2019年6月30日，共715个 交 易日。以2016年8月23日—2018年8月31日 为样本内的样本点，以2018年9月1日—2019年6月30日为样本外的样本点。使用5 min和日收盘价交易数据，第t天5 min收盘价表示为Pt，i，i=1，2，…，48，Pt为第t天的收盘价。数据来自Wind数据库，使用Matlab和R编程软件。

第t天的5 min收益率为

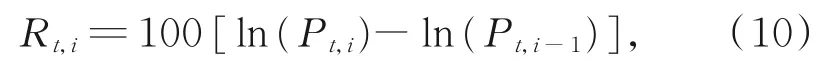
第t天的日收益率为

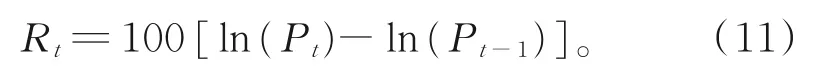
根据ANDERSEN等［8］的定义，将第t天所有高频数据收益率的平方和作为已实现波动率的估计：

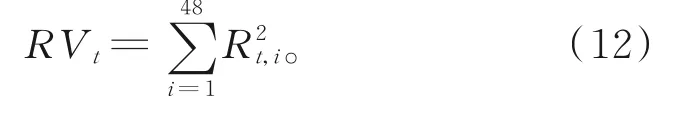
由于投资者情绪的涵盖面很广，其度量方法差异巨大，一种普遍的做法是沿用B-W方法，即利用代理变量［16］，采用主成分分析法对投资者情绪进行度量。根据沪深300成分股市场的实际情况及数据的可获得性，选取沪深300指数换手率Turn、市盈率PER、涨跌幅Updown、消费者信心指数CCI和成交量Volume作为代理变量。由于现期投资者的行为决策不仅受当期代理指标的影响，也受前一期代理指标的影响。故用主成分分析法对上述5个代理变量的当期Turnt，PERt，Updownt，CCIt，Volumet及其 滞 后 期Turnt-1，PERt-1，Updownt-1，CCIt-1，Volumet-1进行分析，因前3个主成分累积贡献率达85.5%，故取前3个主成分的加权平均生成初始情绪指数SENT1，然后分别对SENT1与上述5个代理变量的当期和滞后期进行相关性分析，如表1所示。

表1 初始情绪指数SENT1与代理变量之间的相关性Table 1 Correlation between SENT1 and surrogate variables

由表1可知，两期代理变量中，相关程度相对较高 的 分 别 为Turnt-1，PERt-1，CCIt-1，Volumet-1及Updownt，将其作为投资者情绪指数代理指标。将筛选出的5个代理指标与居民消费价格指数和宏观经济景气一致指数进行正交，以剔除宏观经济变量的影响。采用主成分分析法，发现前3个主成分的累积贡献率达98.9%，故取前3个主成分的加权平均，计算沪深300投资者情绪指数序列SENT：

其中，加权平均系数为对应主成分的方差贡献率。

图1为收益率、已实现波动率与投资者情绪指数的时序图，可知，根据B-W方法构造的投资者情绪指数与收益率、已实现波动率的波动起伏极其相似，当收益率上涨较大时，投资者情绪指数也相对较大；当收益率下降较多时，投资者情绪指数相对也较低。因此，投资者情绪指数能在一定程度上刻画沪深300成分股市场中的投资者情绪。

图1 收益率、已实现波动率与投资者情绪指数的时序图Fig.1 Time series of return，realized volatility and sentiment index

表2为沪深300成分股的收益率、已实现波动率和投资者情绪指数的描述性统计结果。在Jarque-Bera（J-B）正态性检验中，三者均在1%显著性水平下拒绝原假设，具有尖峰厚尾的分布形态，不服从高斯正态分布。因此，后续实证研究采用t分布拟合序列，同时不失一般性，取γ=1，即

表2 收益率、已实现波动率和投资者情绪指数的描述性统计Table 2 Descriptive statistics of return，realized volatility and investor sentiment index series

表3为日收益率、已实现波动率和投资者情绪指数序列的长记忆性检验结果，滞后5，10，20期均存在显著的自相关性；GPH检验为0～0.5，进一步证明了沪深300成分股存在长记忆性，同时对已实现波动率和投资者情绪指数序列进行了GPH检验，发现其同样具有长记忆性，说明金融资产价格的波动和投资者情绪具有持续性和依赖性，当期价格波动、投资者情绪易受滞后期价格波动、投资者情绪影响，进而影响未来。

表3 日收益率、已实现波动率和投资者情绪指数序列的长记忆性检验Table 3 Long memory test of daily return，realized volatility and investor sentiment index series

2.2 HAR-RV（-SENT）GAS模型的参数估计和拟合分析

基于投资者情绪，建立HAR-RV GAS和HAR-RV-SENT GAS模型。参照文献［2］，采用极大似然估计法对所有参数进行估计。

自相关函数值可反映金融时间序列的长记忆程度。通过描绘不同模型的自相关系数拟合值（理论值）和样本自相关系数（实际值）（图2），研究序列的自相关结构。由图2可知，包含更多原本信息的模型其自相关函数的理论值更接近实际拟合值。

图2 不同模型下自相关函数理论值与实际值Fig.2 Theoretical and practical autocorrelation function of conditional variance in different models

图3为模型的波动率拟合结果，相对于RV模型，GAS类模型更能捕捉波动率的尖峰厚尾和集聚性，波动率拟合能力有明显提升；而包含投资者情绪和已实现波动率的HAR-RV-SENT GAS模型具有更优的波动率特性刻画能力。表4列出的GAS类模型的参数估计结果显示，HAR-RV-SENT GAS模型的似然函数值较其他2种模型略有提升。

表4 GAS、HAR-RV GAS和HAR-RV-SENT GAS模型的参数估计结果Table 4 Parameter estimation results of GAS，HAR-RV GAS and HAR-RV-SENT GAS models

图3 模型的波动率拟合结果Fig.3 Volatility fitting results of models

2.3 波动率预测分析

相较模型拟合效果，模型的预测能力更值得关注。采用哪种损失函数计算度量偏差最合理，学术界尚无定论。大量研究表明，以多种损失函数作为判别标准以及采用Bootstrap方法获得SPA检验统计量，具有更优的预测判别能力，且结论的稳健性更好。因此，将5种损失函数作为模型预测的评价标准，记为Li（i=1，2，…，5），具体定义为

对前485个样本点做估计，对后230个样本点做预测，即H=485，M=230。采用滚动时间窗法进行波动率预测，取SPA检验统计量的渐近分布参数B=2000，q=0.5。3种模型的SPA检验结果如表5所示，限于篇幅，相关SPA检验理论请参见文献［24-25］。由表5可知，HAR-RV-SENT GAS模型的预测精度最高。

表5 GAS、HAR-RV GAS和HAR-RV-SENT GAS模型的SPA检验结果Table 5 SPA test results of GAS、HAR-RV GAS and HAR-RV-SENT GAS models

图4为模型的波动率预测值，由图4可知，HAR-RV-SENT GAS和HAR-RV GAS模 型 在波动率预测方面比GAS模型略好，在波动起伏剧烈时，更能反映尖峰厚尾的特征，对波动的反应更敏锐，能够更好地捕捉市场动态。

图4 模型的波动率预测值Fig.4 Volatility forecast of models

综上可知，HAR-RV-SENT GAS模型对沪深300指数收益序列的波动率具有更优异的刻画和样本外推预测能力，对未来长期波动率有更好的解释能力。

2.4 VaR预测分析

VaR是市场风险管理中最广泛使用的度量工具之一，具有简单、直观和易于计算等优点，风险管理者和相关金融部门均通过VaR值判断和规避市场风险。其原理是在给定的置信水平下，估计金融资产在未来价格波动时可能出现的最大或潜在损失。在给定置信水平1-α下t+1时刻的VaR定义为

由此可得VaR计算式为

其中，μ为收益率序列的均值，tα为收益率分布的α分位数，σt+1为GAS类模型预测得到的t+1时刻条件异方差经开方得到的标准差。若VaR为负值，则表示损失。

为增强研究结论的可靠性，在实证检验时，分别选取置信水平1-α为90%，95%，97.5%，99%，99.5%，99.75%，得 到GAS、HAR-RV GAS和HAR-RV-SENT GAS模型的VaR预测结果。为节约篇幅，本文仅展示置信水平为95%和99%时的实际收益率及VaR预测结果，分别见图5和图6。可知，加入已实现波动率和投资者情绪指数的HAR-RV-SENT GAS模型能充分利用高频数据和投资者情绪信息，提高VaR预测精度。

图5 置信水平为95%时沪深300指数的VaR预测结果Fig.5 VaR prediction results of CSI 300 index when confidence level is 95%

图6 置信水平为99%时沪深300指数的VaR预测结果Fig.6 VaR prediction results of CSI 300 index when confidence level is 99%

用模型比较技术评估波动率模型风险预测的精度和选择VaR预测能力最佳的模型。由损失函数对模型进行排序，采用VaR模型比较中最常用的分位数回归的分位数损失（QL）[26]。具体地，在给定置信水平1-α下t+1时刻VaR预测的分位数损失函数为

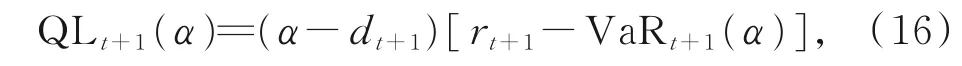
其中，

通常称之为碰撞序列（hitting series），其含义为如果t时刻的实际收益率小于VaR预测值，那么该序列t时刻的取值为1，否则为0。显然QL是非对称损失函数，当实际收益率超过VaR预测值时，根据权重α进行惩罚。在预测期内对分位数损失取平均，选择平均值较低的模型。模型性能的优劣由其平均分位数损失的比值决定，例如模型A和B的平均分位数损失分别为QLA，QLB，若QLA/QLB＜1，则认为模型A比模型B更优。

表6列出了在不同置信水平下，HAR-RVSENT GAS和HAR-RV GAS模型与GAS模型的平均分位数损失比，可知，该值均小于1，表明HAR-RV-SENT GAS和HAR-RV GAS模 型 的VaR预测精度较GAS模型高。在极端显著性水平下HAR-RV-SENT GAS模型和HAR-RV GAS模型的VaR预测效果更明显。因此，HAR-RV GAS类模型不仅可以刻画样本内波动率的动态变化模式，而且在预测样本外的VaR变化时更胜一筹。

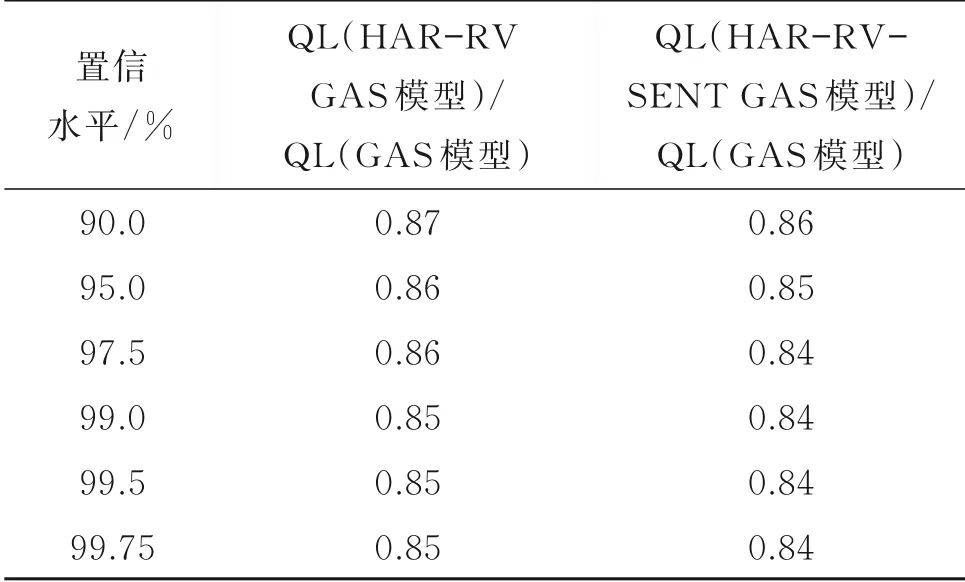
表6 在不同置信水平下HAR-RV GAS和HARRV-SENT GAS模型与GAS模 型的平均分位数损失值Table 6 The ratio of average quantile loss of HAR-RV GAS，HAR-RV-SENT GAS models and GAS model in different confidence level

3 结论

以沪深300指数的5 min高频数据为实证样本，提出了一种基于已实现波动率和投资者情绪的波动率模型。同时，为验证该模型的有效性，通过自相关函数值的对比和SPA检验，探究模型的波动率拟合和预测能力。探讨了该模型在VaR计算中的性能，并通过VaR预测值和平均分位数损失，实证对比了该模型与GAS模型的VaR预测精度。

实证结果表明：（1）总体讲，GAS类模型无论在波动率刻画还是在VaR预测上表现均较好，HAR-RV GAS模型较GAS模型能更好地描述波动率的长记忆性，而加入已实现波动率和投资者情绪的HAR-RV-SENT GAS模型表现更好。（2）当市场处于风险时，HAR-RV-SENT GAS模型和HAR-RV GAS模型均较GAS模型具有更高的风险预测精度，其中HAR-RV-SENT GAS模型的VaR预测精度略高于HAR-RV GAS模型。实证结果表明，加入已实现波动率和考虑投资者情绪的模型可显著改善沪深300成分股市场的VaR预测效果。因此，本文的研究方法和结论为GAS模型在金融学研究中的进一步应用提供了可能。

本文尚存在不足之处。首先，仅与GAS模型对比，未与其他高频波动率模型比较。其次，没有考虑分布的非对称性，也没有引入杠杆机制的波动率模型，且在HAR-RV GAS类模型与GAS模型的波动率预测优越性方面缺乏理论证明。最后，仅以沪深300指数为实证研究对象，样本欠丰富，本文的研究结论需在更广范围做进一步验证。