SSMT:结合状态空间模型和Transformer的时序预测算法

刘立伟，余绍俊

(1.云南师范大学 信息学院，云南 昆明 650500；2.昆明学院 信息工程学院，云南 昆明 650214)

0 引言

时间序列数据的预测问题在现实生活中随处可见，其中涉及语音识别、噪声控制和对股票市场的研究等，而时间序列预测的目的就是通过对给定的时间序列观测数据进行估计，得出未来某一个特殊时刻点的数值以及概率分布，其本质主要是根据前T个时间的观察数据计算T+时间的序列值。这是风险管理与投资决策领域的一个关键任务，它在统计学、机器学习、数据挖掘、计量经济学、运筹学等许多领域都发挥着重要作用。比如，预测特定产品的供给情况可以用来进行存货控制、车辆调度和拓扑规划，这对于供应链优化至关重要。

时间序列预测的传统统计学模型有 ARIMA 模型、指数平滑方法等。在现代预测中，传统模型不具备从类似的时间序列数据集中推断出共享模式，从而导致了过多的计算任务和大量的人力需求。因此，深度学习以其提取高级特征的能力进入了人们的视野。

关于时序预测的深度学习方法可以分为使用自回归模型的迭代方法[1-3]或基于序列到序列模型的直接方法[4]。随着注意力机制的发展[5]，长期依赖性学习获得许多改进，其中Transformer架构在多个自然语言处理应用中实现了最先进的性能[6-8]。因此，基于Transformer的模型架构获得了越来越多的关注[3]。

Transformer模型依靠注意力机制来映射输入和输出之间的全局依赖关系，从而拥有更强的并行化能力。递归模型固有的顺序性阻碍了训练的并行化，而在较长序列的研究中，由于内存的限制，并行化至关重要。Transformer使用的注意力机制使其成为时间序列预测的良好预选方法，因为它可以捕捉到长期和短期的依赖关系，并且不同的attention-heads可以学习到时间序列的不同方面。然而，机器学习方法容易出现过度拟合[9]。因此，较简单的模型有可能在低数据状态下做得更好，这在具有少量历史观测数据的预测问题中特别常见(例如季度性宏观经济预测)。

最近深度学习的一个趋势是开发混合模型，混合模型在各种应用中都显示出比纯统计或机器学习模型更好的性能[10-11]。混合方法将经过充分研究的统计学模型与深度学习结合在一起，即使用深度神经网络在每个时间步骤生成传统模型参数。混合模型利用先验信息为神经网络训练提供信息，减少网络的假设空间，提高泛化能力，因此对小数据集特别有用。因为在小数据集中，深度学习模型存在较大的过拟合风险。

为了在小数据集上获得更好的预测效果，本文在现有算法的基础上，提出了状态空间模型Transformer联合的时间序列预测算法并命名为SSMT。具体贡献如下：(1)充分运用状态空间模型Transformer的优势设计了一个全新的时序预测算法，并在OMI realized library数据集中通过预测股票指数的波动展现了比现在最先进的基准更为优秀的效果。(2)通过使用Transformer将数据特征映射为状态空间模型的参数，使算法具有更强的先验信息，从而在小数据集上具有更好的效果。(3)针对在时序预测过程中，RNN网络所存在的对长期依赖学习能力较差以及对内存约束导致速度下降等问题，充分展现了Transformer对长短期时间序列的学习和并行化计算能力。

1 相关文献

1.1 时序预测研究

由于时序预测的广泛应用，人们提出了各种方法来解决预测问题。其中ARIMA[12]是最突出的模型之一。它的统计特性以及模型选择过程中的Box-Jenkins方法[13]使其成为研究人员的第一个尝试。然而，其采用的线性假设和有限的可扩展性使其不适合大规模的预测任务。此外，由于每个时间序列都是单独拟合的，所以类似的时间序列之间的信息不能共享。为了解决这个问题，Temporal Regularized Matrix Factorization[14](TRMF)将相关的时间序列数据建模为一个矩阵，并将预测作为一个矩阵分解问题来处理。Effective bayesian modeling of groups[15]中提出了分层贝叶斯方法，从图模型的角度在多个相关的时间序列中进行学习。

深度神经网络的出现，使研究者可以使用它捕捉相关时间序列的共享信息，从而进行准确的预测。Deepar[2]通过编码器-解码器的方式对概率分布进行建模，使用堆叠的长短期记忆[16](Long Short-Term Memory, LSTM)层来生成一步到位的高斯概率分布的预测，将传统的AR模型与RNN融合在一起。相反，Multi-horizon Quantile Recurrent Forecaster(MQ-RNN)使用循环神经网络作为编码器，多层感知器(MLPs)作为解码器，以解决所谓的误差积累问题，并且并行进行多步预测。Deep factors with gaussian processes中对每个时间序列使用局部高斯过程处理噪声，同时使用全局RNN对共享模式进行建模。

最近，基于Transformer架构的自注意力机制(self-attention)被用于序列建模，并取得了一定成果。ConvTrans[3]提出使用卷积层进行局部处理，并使用稀疏注意机制来增加预测期间的感受野的大小。Informer[17]提出了ProbSparse Self-Attention，减少了模型运算时的时间复杂度和空间复杂度，以解决长序列时间序列预测问题(Long sequence time-series forecasting, LSTF)中随着时间序列长度的增加模型性能和预测准确性下降的问题。

1.2 状态空间模型

状态空间模型(State Space Models)通过隐藏状态lt∈L对数据的时间结构进行建模，该隐藏状态可以用来对序列中的水平、趋势或季节性模式等组成部分进行编码，并且在预测时应用于单个时间序列。一般的状态空间模型通常包括一个状态转移方程和一个观测模型，状态转移方程描述了隐藏状态随时间变化的规律，即p(lt|lt-1)；观测模型则描述了给定隐藏状态下观测值的条件概率分布，即p(zt|lt)。

SSMT使用的是线性高斯状态空间模型，其状态转移方程为

lt=Ftlt-1+ωtεt，εt～N(0,1)

(1)

观测模型为

zt=Htlt+bt+υtt，εt～N(0,1)

(2)

其中Ft∈L×L是状态转移矩阵，是状态转移噪声的强度，Ht∈1×L以及bt∈是观测模型的权重和偏置，υt∈+是观测噪声的强度。初始状态

综上所述，线性高斯状态空间模型完全由以下参数决定

Θt=(Ft,Ht,ωt,bt,υt,μ0,σ0)，∀t>0

(3)

1.3 Temporal Fusion Transformers时序预测算法

Temporal Fusion Transformers(TFT)是一种基于注意力机制的网络新架构[18]，它将高性能的多步时间预测与对时间动态的可解释性洞察力结合起来。为了学习不同尺度的时间关系，TFT使用循环层进行局部处理，使用可解释的自注意力层进行长期依赖学习。TFT利用专门的组件来选择相关的特征，并利用一系列的门控层来抑制不必要的组件，从而在广泛的场景中实现高性能表现。在各种真实世界的数据集上，TFT都展示了比现有基准更为显著的性能改进。

为了获得比最先进的基准更显著的性能改进，TFT引入了多种新的想法，以使该架构与多步时间预测中常见的所有潜在输入和时间关系保持一致，具体而言，包括(1)静态协变量编码器(static covariate encoders)，该编码器对静态变量进行编码，以供网络的其他部分使用；(2) 贯穿始终的门控机制和样本相关变量选择，以最小化不相关输入的贡献；(3) 通过使用sequence-to-sequence层，可以局部处理已知和观察到的输入；(4) 通过在时间上的自注意力解码器，以学习数据集中存在的长期依赖。这些专门组件的使用也促进了可解释性，特别是帮助用户在识别(i)预测问题的全局重要变量、(ii)持续的时间模式，和(iii)重要事件这3个方面。

2 SSMT模型

针对使用Transformer架构模型进行时间序列预测在数据量不足的小数据集上准确率下降的问题，本文提出能够将状态空间模型与Temporal Fusion Transformers(TFT)模型融合后进行联合预测，网络结构如图1所示。在训练过程中，网络的输入是特征X1到XT，通过TFT Encoder进行编码，然后在TFT Decoder中和输入的时不变特征XT+1到XT+T一起计算出高斯状态空间模型的参数ΘT+1到ΘT+T，最后根据已知的观测值ZT到ZT+T，使用公式(4)到公式(13)，通过最大化似然函数来更新模型参数。在预测时，X1到XT经过TFT Encoder编码，再结合时不变特征XT+1到XT+T经过已经学习到参数Φ的网络输出预测值的概率分布，再经过多次采样输出预测值。

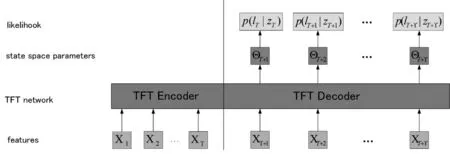
图1 SSMT模型架构

具体来说，预测可分为3个步骤。

第一步先将时间序列数据通过TFT架构，从而将特征映射为状态空间模型的参数；

第二步再使用状态空间模型预测序列在每个时间步上取值的概率分布；

第三步通过对预测的概率分布进行多次采样生成对未来一段时间数据的预测。

SSMT正是通过这种网络结构使模型能在大量的序列和特征中学习到相似的模式。

2.1 模型原理

SSMT通过学习一个对于所有时间序列共享的网络参数，直接用TFT网络计算高斯状态空间模型参数Θt=TFT(xt)。得到Θt后，观测值Z1:T即按照下面的公式分布。

p(Z1:T|Θ1:T,Φ)=pss(Z1:T|Θ1:T)

(4)

其中Φ为模型学习到的参数，pss表示线性状态空间模型下的边际似然函数，由以下公式可得出。

(5)

根据卡尔曼滤波，又可得到

(6)

公式(6)中各参数推导关系如下

(7)

(8)

(9)

(10)

(11)

(12)

Pt|t=Pt|t-1-KtHtPt|t-1

(13)

2.2 模型训练

模型参数Φ是通过最大化训练范围内数据ZT+1:T+T的对数似然函数来学习的，似然函数如公式(4)所示。例如，最大化对数似然：Φ*=argmaxΦZ(Φ)，其中

Z(Φ)=∑logp(ZT+1:T+T|X1:T+T,Φ)

=∑logpss(ZT+1:T+T|ΘT+1:T+T)

(14)

将公式的结果看作一个损失函数(值可能为负)，用来衡量给定X1:T+T的情况下由TFT生成的高斯状态空间模型参数ΘT+1:T+T与真实观测值ZZT+1:T+T之间的兼容性。这些参数可以通过卡尔曼滤波用标准似然计算得出，如公式(7)～(13)，它主要包含了矩阵和矩阵，矩阵和向量之间的运算，因此可以使用pytorch神经网络框架来进行对数似然函数的计算，并基于梯度下降对模型参数进行优化。

2.3 模型预测

在模型进行网络参数学习之后，就可以利用学习到的网络参数进行预测了，即解决了如下问题。

p(ZT+1:T+γ|Z1:T,X1:T+T;Φ)

(15)

对给定的时间序列进行概率预测。

在训练步骤中，模型利用时间序列ZT+1:T+T通过卡尔曼滤波计算p(lT+1:T+T|ZT+1:T+T)来获得高斯状态空间模型的参数ΘT+1:T+T，下一步在预测时，模型通过不断自循环获得ΘT+1:T+γ，计算出预测值的高斯分布参数，然后利用蒙特卡洛方法多次重复采样后取平均来得到预测的期望值。

3 实验与结果分析

3.1 实验环境

本次实验使用的软件环境为linux，Python 3.8，Pytorch1.11.0。硬件配置为Intel(R) Xeon(R) CPU E5-2680 v4和 GeForce RTXTM3090 GPU。

3.2 数据集

本次实验为了评估相比传统Transformer架构模型在较小噪声数据集上的性能，这里使用了一个小数据集对金融数据的波动率进行了预测。具体数据集为oxfordmanrealizedvolatilityindices，它包含了31个股票指数每天已实现的波动率值以及它们的每日收益。这些波动率和收益值是通过每一天盘中数据计算出来的。在本次实验中，使用了过去一年(即252个工作日)的信息对下周(即5个工作日)的数据进行预测。

3.3 训练流程

笔者首先将数据集中的时间序列分成了3部分：用于学习使用的训练集，用于调整超参数的验证集以及用于性能评估使用的测试集。超参数优化时使用的参数范围如下所示：

(1)Hidden size - 40，80，120，160，240，320；

(2)Dropout rate - 0.1，0.2，0.3，0.4，0.5；

(3)Batch size - 32，64，128，256；

(4)Learning rate - 0.0001～0.01；

(5)Gradient clip - 0.01，0.1，1.0，100.0；

(6)Num heads -1，4。

最终得到的模型最佳参数配置如表1所示。

3.4 实验结果

笔者将SSTM与多种时序预测模型进行了比较，其中第一类是使用直接方法生成未来预测的模型，包括：(1)具有全局环境变量的简单sequence-to-sequence模型(Seq2Seq)；(2)Multi-horizon Quantile Recurrent Forecaster模型(MQRNN)。第二类是使用迭代方法的模型，包括：(1)DeepAR模型[2]；(2)同样基于Transformer架构的ConvTrans模型[8]。实验结果如表2—3所示。在这里，笔者使用了归一量化损失作为评价指标(P50和P90风险)，计算方法见公式(16)和(17)。

(16)

(17)

表1 模型参数配置

表2 各模型在数据集上的P50 losses

表3 各模型在数据集上的P90 losses

从表2和表3可以看出，在实验所采用的数据集上，SSMT所展现的效果优于其他所有基准模型。在P50分位数上，SSMT的损失相比第二小的TFT降低了15%；在P90分位数上，SSMT的损失相比TFT也降低了15%。

4 结语

文章提出了一个在时间序列预测任务中相比传统Transformer架构对小数据集更加友好的算法——SSMT，它使用Transformer架构与传统统计学公式联合所得，结合了Transformer对于长期依赖的学习以及并行化能力，通过使用深度学习技术从相关时间序列中有效地学习了状态空间模型的参数，并使用状态空间模型计算出模型输出的概率分布从而采样得出最终结果。通过在现实世界金融数据的波动率数据集上测试表明该模型能够在小数据集的预测上取得更为准确的结果，也显示出将一般Transformer架构与高斯状态空间模型相结合的好处。