黑龙江省高等教育体系评价与展望

王广林 张劲松 潘正

摘  要：高等教育系统是否具有可持续性，与一个国家的综合竞争力和未来发展密切相關。纵观近年来的数据，黑龙江省81所高等院校人才培养进程总体发展缓慢。为协调和维持黑龙江省高等教育体系的可持续发展，本文建立了相关评估模型，以推导国家高等教育系统中协调的定量表达以及评估指标之间的多重关系。使用基于熵权的TOPSIS模型对中国各地区的高等教育发展现状进行评估，从高中生毕业人数、高等学校师生比等七个维度对其健康协调程度进行了定量分析。运用灰色模型来预测各种评估指标的数据状态，对收集到的北京市和黑龙江省实测现实进行比较分析，并提出合理可行的策略来推进黑龙江省高等教育系统的可持续发展。

关键词：高等教育;可持续发展;TOPSIS;灰色预测

中图分类号：G64    文献标识码：A    文章编号：1673-7164（2022）01-0006-08

随着新高考制度改革的推进，我国越发重视高等教育的可持续发展。根据中国统计年鉴，政府对高等教育的投资从2010年的5629亿元增加到2019年13464亿元，高等教育发展力度空前。目前，我国高等教育发展存在地区发展不均衡、资金投入差异大、教育机会不协调等关键性制约因素，经过数据收集整理，本文将我国高等教育发展情况大致划分为五类地区，并进行现状概述，具体划分如表1所示。

教育经费投入规模方面。根据2015—2019年面板数据可知，一类地区教育经费投入由2022亿元逐年增长至3189亿元，山东省为首的二类地区，年平均增长约150亿元，表现十分亮眼。黑龙江省所处的三类地区，教育经费投入近五年来平均约六百亿，仅为一类地区投入规模的25%左右。四、五类地区的代表省份，年教育经费投入额仅为200亿元左右，不足三类地区的三分之一。

普通高等学校发展规模方面。广东省与山东省高校数量分别达到154、146所，三类地区中的黑龙江省高校数量为81所，仅为一类地区一半。观察四类地区和五类地区的数据可知，青海与宁夏的高校数量明显少于前三个地区，分别为19所和12所，数量相差更甚。

师资层次方面。广东省和山东省正高级职称人数分别达到了15537和18254人，正高级职称占总高校教师人数比例分别达到9.24%和7.79%，表现优异。而包括黑龙江省在内的三类地区正高级职称人数仅有8000人，远远落后于一二类地区。研究四、五类地区后发现，青海及宁夏地区正高级职称人数仅有不到1000人，数量较一类地区仅占10%不到。

综上，我国高等教育系统呈现出区域化、碎片化的发展态势，东南沿海地区教育资源发达，西北地区及中部地区发展相对落后。五类地区差距极大，因此缩小差距、打造平等高效的高等教育系统可持续发展模式尤为重要。

影响高等教育发展水平的因素不止集中在宏观政策，还包括教育公平、高校水平和经济发展程度等一系列因素，评价维度间相互关联，因此本文基于黑龙江省高等教育发展现状，引入实证分析方法对其进行评价和预测，具有重要的理论意义和实践价值。

一、文献综述

（一）国内文献综述

从高等教育发展的评价方法来看，现有文献对高等教育评价体系的研究较为分散。其中，有部分学者利用DEA模型对高等教育的效率进行了评价。李元静和张谦（2014）运用Malmquist指数法，测度了我国高等教育的发展效率，得出我国高等教育资源配置存在区域差异[1]。张宏（2015）以教育经费、教职工人数作为投入要素，以论文数量、毕业生人数作为产出指标，建立DEA模型，得出我国高等教育发展效率呈现规模报酬递增的趋势，但区域间差异明显[2]。李航（2018）运用DEA-Tobit模型研究了经济发展和教育支持对高等教育效率的影响，得出两者均对高等教育效率有着正向影响的结论[3]。此外，也可运用层次分析法（周浩波，2014）[4]、指数分析法（毕吉利，2020）[5]、熵权法TOPSIS模型（柯文进、王军，2020）[6]对高等教育发展水平进行评价。以往文献研究所选取的评价方法主观因素较强，且未针对指标的异质性进行评价方法的调整，故具有可优化的空间。

从高等教育影响因素的效应来看，大多数学者使用计量方法，如马明宇（2020）运用计量回归的分析方法，从经济情况、教育资源投入、产业结构等角度研究了影响高等教育发展的主要因素[7];陈春平和胡何琼（2021）基于国民经济和高等教育等相关的面板数据运用回归分析和灰色关联分析，研究了2000—2019年高等教育结构与经济发展的关系[8];潘兴侠（2020）运用基于熵权的加权模糊隶属度模型评价了我国区域高等教育发展水平，利用空间计量的分析方法对高等教育的因素影响进行了分析[9]。以往的研究成果重点考虑了现有因素对高等教育水平发展的影响，未对未来高等教育发展情况予以反馈，且一定程度上忽视了因素对高等教育的模糊关系，故本文在这些方面弥补了现有文献的不足。

（二）国外文献综述

从研究内容来看，国外主要研究集中于高等教育影响因素、高等教育效率、教育资源分配不均等方面。Jourado（2013）运用AHP层次分析法研究得出，学校环境和社会发展是影响高等教育基础阶段的主要因素[10]。Berchin（2017）研究了巴西联邦高等教育结构体系，得出基础设施、文化体系促进了高等教育的可持续发展[11]。Al-Rahmi（2018）收集了马来西亚723名研究生的问卷调查结果，得出社交媒体的运用和积极的合作学习，能够促进高等教育学习和发展的结论[12]。以往国外文献主要研究某一种因素对高等教育体系的影响，在全面评价高等教育发展方面存在一定的研究空白。

从研究方法来看，国外主要是通过构建一系列指标，基于传统统计方法加以测算与分析。国外学者大多运用数据包络方法对高等教育的效率进行测算，其中包括高校资源配置效率（Johnes，2006a）、办学效率（Cherchuye Laurens，2009）成本效率（Johnes，2006b）[13-15]等。此外，Qian和Smyth（2008）计算了基尼系数和泰尔指数，用以分析中国教育资源区域分配差异不断扩大的原因[16]。Yue（2015）通过描述性分析和回归分析，研究了中国教育在发展中的不平等情况[17]。以往外文文献主要利用数据包络分析方法测算高等教育效率，重点在于研究高等教育投入与产出的关系，本文将研究重点放在全面衡量教育发展上，对于仅研究投入与产出更具有可持续发展意义。

为了对现有研究进行补充，本文主要针对以下三个方面进行深入研究。第一，使用定量分析方法，利用基于熵权的TOPSIS模型和灰色关联度矩阵对我国31个省（市、自治区）高等教育发展水平进行了综合评价，并运用灰色预测对重点研究省份未来十年高等教育发展水平进行预测和分析，具有相对明显的政策意义。第二，选取七项对高等教育发展影响较大的指标进行计算分析，指标选取方法合理，评分结果较为准确。第三，本文在地区异质性的基础上重点对比黑龙江省与北京市，从时间和影响因素方面进行了分析，为黑龙江省高教研究提供了新的思路。

二、模型建立

（一）基于熵权的TOPSIS模型

TOPSIS法（Technique for Order Preference by Similarity to Ideal Solution）亦称理想解法，简称为优劣解距离法，是一种有效的多指标评价方法（彭勇行，2000;Chen，2000;OLSON，2004）[18-20]。这种方法通过构造评价问题的正理想解和负理想解，即各指标的最优解和最劣解，通过计算每个方案到理想方案的相对贴近度，即靠近正理想解和远离负理想解的程度，来对方案进行排序，从而选出最优方案（Deng，2000;陈雷、王延章，2003）[21-22]。TOPSIS 法是一种多目标决策方法，能充分利用原始数据的信息，结果能精确地反映各评价方案之间的差距（Ta-Chung和Chu，2002;Opricovic和Tzeng，2004）[23-24]。

1. 正向化的矩阵标准化。假设有m个要评价的对象，n个评价指标（已正向化的）构成的正向化矩阵如下：

X=

那么，对其标准化的矩阵记为Z，Z中的每一个元素：

Zij=

2. 评价对象的得分。假设有m个要评价的对象，n个评价指标的标准化矩阵：

Z=

则基于熵的标准化矩阵为：

Aij=Zij×Wj=

×

定义最大值：

A+=（a+

1 a+

2 …  a+

n）

=（max{a11，a21，…，am1}，max{a12，a22，…，am2}，…max{a1n，a2n，…，amn}）

定义最小值：

A- =（a-

1 a-

2 …  a-

n）

=（min{a11，a21，…，am1}，min{a12，a22，…，am2}，…min{a1n，a2n，…，amn}）

定义第i（i=1，2，…，m）个评价对象与最大值的距离D+

i=

定义第i（i=1，2，…，m）个评价对象与最小值的距离D-

i=

那么可以计算出第i（i=1，2，…，m）个评价对象未归一化的得分：Si=，0⩽Si⩽1，Si越大D+

i越小，越接近最大值。

3. 指标正向化。采用 = 将极大型指标正向化，将极小型指标按照转化成极大型指标，然后再将指标正向化处理。

（二）灰色关联度矩阵

由于灰色关联度是分析一定向量与向量之间以及矩阵与矩阵之间的关联度（焦玥、胡劲松，2005）[25]，而且所需要的原始数据较少，原理简便（Liu S F和 Liu Y，1998;Hong，1996）[26-27]。关联度是某一个待比较的数列与参照物之间的相关程度。假设现有一组参考数列如下：

xj=（xj（1），xj（2），xj（3），…，xj（k），…，xj（n）），j=1，2，3，…，s

假设一组待比较数列如下：

xi=（xi（1），xi（2），xi（3），…，xi（k），…，xi（n）），i=1，2，3，…，t

則定义关联系数如下：

ε（k）=

（1）ε（k）表示的是第i个比较数列与第j个参考数列第k个样本之间的关联系数。

（2）min minxj（k）-xi（k）和max maxxj（k）-xi（k）表示的是参考数列矩阵与比较数列矩阵数值作差之后的最小值和最大值。

（3）xj（k）-xi（k）被称为“Hamming距离”，其倒数被称为反倒数距离，灰色关联度的本质就是通过反倒数大小来判定关联程度的。

（4）分辨率ρ通常约定俗成取值在[0，1]之间，不过并非表明ρ只能在[0，1]之间。

定义相关度为：r=

r为相关度，有正面作用的为正相关，反之为负相关。

r大于0.7为强相关，小于0.3为弱相关。

如果把xj与xi之间的相关度写成矩阵的形式，则有：

R=

根据R矩阵的结构可以很清楚地知道，待比较的数列从列可以看出其作用大小，参考数列从行可以看出其受影响程度的大小，依据R矩阵数值大小可以分析出比较数列矩阵中哪些数列起到主要作用。

（三）灰色Verhulst（即Logistic）预测模型

在此模型中本文设非负原始序列为X （0 ）={x（0 ）（1），x （0 ）（2），…x （0 ）（n）}，X （1 ）={x （1 ）（1），x （1 ）（2），…x （1 ）（n）}，为1-AGO其序列，其中x （1 ）（k）=x （0 ）（i），Z （1 ）={z （1 ）（1），z （1 ）（2），…z （1 ）（n），}为模型中x （1 ）的紧邻均值生成序列，其中z （1 ）（k）=，k=2，3，…，n。

设X （0 ）为原始序列，X （1 ）为X （0 ）的1-AGO，Z  （1 ）为X （1 ）的紧邻均值生成序列，则称：

x （0 ）（k）+az （1 ）（k）=b（z （1 ）（k））2

为灰色Verhulst模型（蒋红梅和魏勇，2015;李晔和丁圆苹，2020）[28-29]。

称+ax （1 ）（t）=b（x （1 ）（t））2为灰色Verhulst模型的白化方程。

根据灰色Verhulst模型，在最小二乘意义下可以估计出参数a，b的值，再将a，b的估计值代入灰色Verhulst模型的白化方程，在初始条件x （1 ）（1）=x （0 ）（1）下，解得灰色Verhulst模型的时间响应式为：

（1 ）（t+1）=

经过累减还原为 （0 ）（k+1）= （1 ）（k+1）- （1 ）（k）。

三、指标选取与数据来源

影响高等教育的因素可分为直接因素和间接因素。后备人才使用情况、高等学校教育经费投入情况、师资情况、培养方向情况以及高等教育教学效率是高等教育可持续水平的直接影响因素，五项评价指标均源自高等教育体系本身，为直接抽取因素;将地区人均可支配收入水平和科研水平定义为间接影响因素，原因在于二者分别依据经济与教育成果层面引入评价体系，与地区高等教育可持续发展模式未建立直接关系。影响高等教育可持续发展水平的两类因素直观展示如图1所示。

1. 后备人才使用情况。本文选取普通高中毕业生人数与高等学校招生人数比反映某城市生源情况。该指标的选取目的在于综合度量某一地区高等教育后续发展体量与普通高中输出人才中流入本地区高等教育体系的规模，为负向指标，指标数值越低，本地区高等教育可持续发展能力越强。

2. 高等学校教育经费投入情况。经济基础决定上层建筑，高等学校科研基金投入与可持续发展模式建设成正比，稳健的资金支持可以优化学科建设、提升教师水平、完善基础设施。

3. 高等教育教学效率。本文选取高等学校师生比来反映教学效率。由应用型向研究性转变是高等教育体系可持续发展模式建设的一大重要环节，基础阶段开展通识博雅教育，专业阶段实施有针对性的教育方式，降低师生比尤为关键。

4. 师资情况。本文选取教研团队正高级职称人数占比反映高校师资情况。优化教师团队对高等教育体系可持续发展具有关键意义，先进的教学理念与科研实力能够引导出高效的学术环境，提升学生与教师的科研能力。

5. 培养方向情况。选取高等学校本科生与研究生人数比作为高校培养方向可持续性的反映。高等学校本科生培养方案为面向应用型人才，硕士、博士研究生的培养方案为研究性人才。发展能够继续投身高等教育体系的高科技人才，才可以使高等教育体系更加可持续发展。

6. 地区人均可支配收入水平。该指标源于社会经济活动对教育文化体系的促进作用，某一地区人均可支配收入越多，公民可用与高等教育体系的资金便越充足，以此在一定程度上可以弥补政府教育经费不足的问题，增加高等教育体系后续发展的供给动力。

7. 科研水平。以专利授权数量作为某城市科研水平的代表。上述六项指标主要侧重于衡量高等教育体系的活动过程，致力于以先进的外部环境推动该体系可持续发展。此项指标重在评价产出成果，一个地区的专利授权数量一定程度上代表该地高等教育的科研水平，专利授权数量越多，科研实力越雄厚。

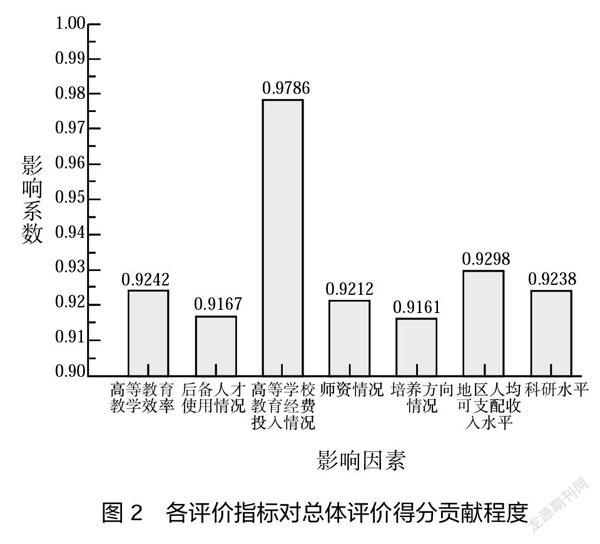
根据上述评价结果，本文利用灰色关联度分析计算出各指标对高等教育系统可持续发展能力综合得分的影响程度，具体情况如图2所示。

由上图可观察出各评价指标的关联系数均在0.9以上，进一步说明本文在指标选取层面上的合理性。

四、实证分析

（一）全国层面各省份综合评估结果的分析

根据实证分析结果，广东省的综合评估得分为0.0688，位居全国第一。从各指标影响数值可以看出，与北京市相比，广东省只有教育经费一项高于前者，而广东省綜合得分超越北京市。由此可见，教育经费投入这项指标为对综合得分关联系数最大的影响因素，从灰色关联度分析结果也可证明，此项指标关联系数为0.9786，为首要评价指标。

深入观察黑龙江省与辽宁省的各项数据发现，除教研团队正高级职称人数占比与普通高中毕业生人数与高等学校招生人数比两项外，其余五项评价指标辽宁省均优于黑龙江省，但黑龙江省最终得分却高于辽宁省;且教研团队正高级职称人数占比两者相差甚小，仅为0.018。说明普通高中毕业生人数与高等学校招生人数这项指标是十分重要的，利用本文建立的实证模型亦可看出，其影响系数为0.9242，位列第三。

社会发展的根基在于经济，经济发展水平高的省市，人均可支配收入随之相应较高。该指标位居前三的省市分别为上海市、北京市和浙江省，而这三个地区的最终综合评价得分亦居于全国前列。通过实证分析计算出该指标对总体得分的贡献程度为0.9298，位列各项指标第二。依据TOPSIS模型得到，全国各地区高等教育体系可持续发展能力综合评分基本与经济发展水平及人口分布情况相匹配，以黑河-腾冲线为界，东部地区总体情况明显优于西部各地的TOPSIS得分。

广东省、江苏省与浙江省经济发展总量均居于全国前五位，根据本文TOPSIS模型计算的高等教育发展能力得分亦位列前五，由此更加充分地表明经济发展水平对高等教育体系的贡献程度，证明本文间接评价指标选取的合理性。北京市为全国政治与文化中心，上海市为经济、金融及航运中心，高等教育综合得分与其国家定位相吻合。

部分西部省区没有一所世界一流大学A类建设高校，人才流失、经济落后、科研环境艰难以及教师资源匮乏等定性因素均表明其高等教育发展模式存在严重问题，TOPSIS综合得分亦位居全国尾部，地方政府及国家教育系统应“因地制宜”，予以发展动力。

（二） 黑龙江省高等教育可持续发展模式对比分析

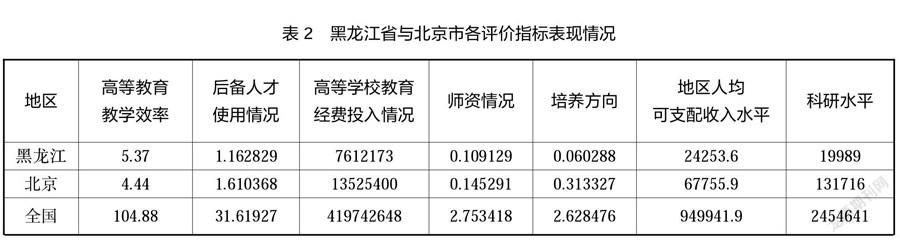
本文依据所得到的数据，进行了黑龙江省与北京市及全国指标数值的横向对比，如表2所示。

纵观黑龙江省各项指标得分数据，高等学校教育经费投入情况、高等学校本科生与研究生人数比、地区人均可支配收入、专利授权数量四项指标得分低于全国各省市平均值，应引起地方政府高度重视，尤其是高等学校教育经费投入情况，黑龙江省为7612173，全国平均为13540085，仅为全国平均的一半左右;专利授权数量黑龙江省为19989，全国平均为79182，仅为全国平均的四分之一左右。

北京市的综合评价得分为全国第三，各项指教表现均衡，且作为全国政治、文化和教育中心，均有不可替代的模式优化辐射作用。本文选择北京市作为参照对象，在优化黑龙江省高等教育体系可持续发展模式的基础上，为全国各地区提供了一个具体思路，以供他方进行参考。

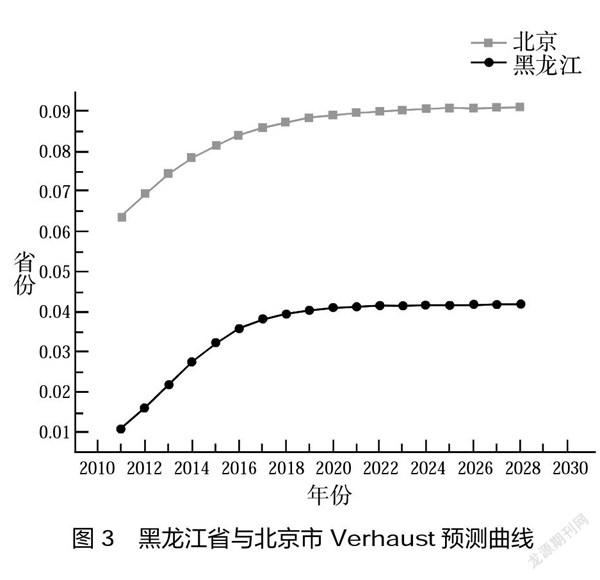
根据历史数据并加以修正，本研究预测黑龙江省2020—2029年高等教育体系可持续发展能力综合得分呈增长趋势，虽整体增长速度较快，但发展基数体量仍然较小，故最终得分较低，为0.0303，远低于北京的0.0579，北京的高等教育体系整体发展体量大且增长速度较快。对于北京市和黑龙江省的灰色Verhulst模型预测曲线，如图3所示。

2015年10月24日，国务院印发《统筹推进世界一流大学与世界一流学科建设总体方案》，在“双一流”建设期间北京地区高校投入教育经费预算增长远高于全国平均水平31.21%，北京投入近百亿推动高校高精尖创新中心建设，有8所高校教育经费增长位列前五十，而黑龙江高校没有上榜。在“双一流”建设收官之年，北京与黑龙江的高等教育可持续发展能力综合得分差距进一步被拉大。

北京的教育经费得分为13525400，高于黑龙江7612173，黑龙江省教育经费远低于北京的，导致了三方面的影响。第一，科研经费短缺，长期以来，科研经费在高校收入所占比例均处于较低水平，教育经费不足对黑龙江高校科研工作的开展产生了不利的的影响，科研队伍建设及科研设备的配备难以满足高校科研需求，制约了以理工科高校为主的黑龙江高校高水平研究工作的开展。第二，图书资源、校舍建筑等硬件资源配备不足，由于教育经费投入有限及学生数量的不断增加，高校图书馆普遍存在图书资源过于陈旧，不符合时代发展要求的问题，图书资源少有更新，学生难以通过阅读了解前沿科学研究。生均校舍面积和校舍环境均低于北京等较发达地区，新建建筑较少。第三，实验仪器与设备短缺，就黑龙江省高校专业设置来看，理工科学生占大多数。众所周知，实验仪器与设备对于理工科教学来说是不可或缺的，但由于经费等原因，学校不能正常配备实验仪器设备，仪器设备无法满足师生的实践和科研需求。应积极推动“世界一流大学和一流学科”建设，合理配置和利用教育经费，加大工业、农业等行业高校科研经费和创新成果转化经费投入，鼓励创新成果转化，服务“新时代东北全面全方位振兴”和“耕地保护”战略。

专利数量是地区高等教育水平的重要体现，黑龙江省86247低于北京得分527390，反映出黑龙江省的高等教育水平及科研创新能力较弱，黑龙江省应保护技术交易市场，建立健全技术交易制度，对技术交易给予一定的税收支持，促进技术的交易。政府还要提高财政科技支持，坚持科教兴国战略，为具有创新力的企业提供更多支持，鼓励并创造更优的外部环境;加大研发经费投入力度，为科研提供稳定支持;因地制宜，合理配置科研经费投入比例。

黑龙江省作为东北老工业基地之一和重要的耕地保护区，高校数量较多，但普遍质量不高，与地区经济发展水平不匹配，教育经费投入和科研能力落后于东南沿海地区，应该高效配置区域内教育资源，支持和鼓励工业、农业类高校发展，实现经济发展与高等教育需求有效对接，在发展高新技术产业的同时，积极发展工业和农业等造血性产业，为承接东部发达地区产业转移服务。另外，黑龙江省人口外流严重，普通省属高校本省招生人数超过50%，毕业留黑龙江省工作人数仅占毕业生人数的30%，应出台相应的人才引进政策，给外地落户群体发放补贴，吸引与经济发展相关的紧缺型本地高校毕业生留黑工作。

五、结论和政策建议

本文基于熵的TOPSIS模型对全国各省高等教育可持续发展水平进行了评估，并利用灰色预测对黑龙江和北京的高等教育发展进行了对比，得到黑龙江高等教育可持续发展的相关结论。第一，黑龙江省在校生数量庞大，高校众多，缺乏与高等院校扩招相匹配的财力保障，高等教育面临教育经费不足的问题。第二，黑龙江省的高等教育水平及科研创新能力较弱。第三，师资层次和人才培养方向决定了教学质量和科研创新程度，黑龙江省尖端人才资源外流严重。

针对黑龙江省教育经费不足的问题，可具体采取以下措施。第一，通过“互联网与人工智能AI”技术发展“互联网+高等教育”，促进教育优势地区与其他地区的学术交流以及教学资源共享，在区域与区域之间构建紧密型高校共同体，弥补黑龙江省与其他教育优势地区的高等教育水平的差距;第二，鼓励学校进行产学研一体化发展，促进行业性高校积极发挥行业内影响力与创造力获取更多的资金投入教学、科研活动;第三，完善教师职称评价标准，发挥正高级教授对于科学研究和产学研融合发展的推动作用;第四，鼓励高等院校与社会企业合作，合理调整学生学费，解決高等教育投入机制中的社会缺位问题;第五，政府应针对不同性质的高校科研环境，相应的调整教学硬件的数量，加大科研投入资金数量，对于图书资源、校舍建筑等硬件资源配备，做到及时供应，为高校师生提供一个良好的科研环境。

要提高黑龙江省教育水平及科研创新，需要做到：第一，对于技术交易市场方面，黑龙江省应积极做好技术交易市场监管工作，维持技术交易秩序，建立健全技术交易制度，对技术交易给予一定的税收支持，促进和保护技术的交易，以提高科研人员的发明积极性;第二，对于技术财政支持方面，政府要加大财政支持力度，制定科研创新奖励政策，为具有创新力的高校提供更多支持，鼓励并创造更优的外部环境;第三，对于科研团队建设方面，黑龙江省有众多优秀的理工科院校，具有一定的科研创新优势，政府应鼓励高校，通过不断壮大研发团队，细化研发职能，在专利研发上彰显专业化来提升研发水平和科技创新能力;第四，对于专利实用性方面，科研创新能力的表现程度，不仅需要依靠数量，更需要依靠质量。应鼓励高校因地制宜，结合地区发展的实际情况，加大研发投入，研发出适合地区的专利产品。

要解决黑龙江省人才引进问题，可从以下几方面着手。第一，对于人才引进落户政策，制定多种落户政策的选择，人才可根据实际情况选择购房或租房优惠补贴政策，吸引人才流入;第二，对于社保补贴政策，对于引入的人才可给予社保50%补贴，一年一补等政策;第三，对于人才税收优惠政策，制定相应的税收优惠及返税政策;第四，对于部分人才匮乏领域，针对相应领域的人才，应加大以上相应优惠政策的力度。

参考文献：

[1] 李元静，张谦. 基于空间SLM模型的高等教育配置效率的实证[J]. 统计与决策，2014（21）：89-92.

[2] 张宏. 提升区域高等教育投入产出效率的对策研究——基于DEA方法和TOBIT模型分析[J]. 教育评论，2015（10）：80-83.

[3] 李航，李成明，白柠瑞，等. “双一流”背景下地区高等教育效率的驱动因素——基于DEA-Tobit模型的实证分析[J]. 技术经济与管理研究，2018（12）：108-112.

[4] 周浩波，刘国瑞，王少媛，等. 高等学校国际化办学水平评价与发展对策研究——基于辽宁17所高校的实证研究[J]. 现代教育管理，2014（10）：1-6.

[5] 毕吉利，周福盛，刘旭东. 基于指数分析法的甘肃高等教育竞争力实证分析及评价（2006 —2017年）[J]. 黑龙江高教研究，2020，38（05）：42-50.

[6] 柯文进，王军. 基于熵权TOPSIS模型的城市高等教育资源承载力评价[J]. 统计与决策，2020，36（18）：50-53.

[7] 马明宇，陈政洋，寇本聪，等. 我国高等教育水平区域差异分析[J]. 合作经济与科技，2020（03）：170-171.

[8] 陈春平，胡何琼. 我国高等教育层次结构优化与经济发展的关系研究——基于2000 —2019年的数据分析[J]. 当代教育论坛，2021（03）：12-18.

[9] 潘兴侠，徐媛媛，赵烨. 我国高等教育发展区域差异、空间效应及影响因素[J]. 教育学术月刊，2020（11）：9-18.

[10] Jurado，C. Z.. Multilevel Analysis of School Performance in Mathematics for Fourth Grade of Basic Education in Colombia[J]. SocEcon，2013（25）：205-235.

[11] Berchin，I. I. . Strategies to Promote Sustainability in Higher Education Institutions[J]. International Journal of Sustainability in Higher Education，2017，18（07）：1018-1038.

[12] Mugahed，W.，Rahmi，A.. A Model of Factors Affecting Learning Performance through the use of Social Media in Malaysian Higher Education[J]. Computers & Education，2018（121）：59-72.

[13] Johnes，J.. Data Envelopment Analysis and its Application to the Measurement of Efficiency in Higher Education[J].  Economics of Education Review，2006，25（03）：273-288.

[14] Cherchye，L.. Efficiency and Equity in Private and Public Education： A Non-parametric Comparison[J]. European Journal of Operational Research，2009，202（02）：563-573.

[15] Johnes，J.. Measuring Teaching Efficiency in Higher Education： An Application to Data Envelopment Analysis to Economics Graduates from UK Universities[J]. European Journal of Operations Research，2006（01）：443-456.

[16] Lei，Q.X.，Russell，S.. Measuring Regional Inequality of Education in China：Widening Coast-inland gap or Widening Rural-urban gap？[J]. Journal of International Development，2008，20（02）：132-144.

[17] Jun，C.Y.. Expansion and Equality in Chinese Higher Education[J]. International Journal of Educational Development，2015（40）：50-58.

[18] 彭勇行. 管理決策分析[M]. 北京：科学出版社，2000.

[19] Chen.，C.T.. Extensions of the TOPSIS for Group Decision Making under Environment[J]. Fuzzy Sets and and Systems，2000（114）：1-9.

[20] Olson，D. L. . Comparison of Weights in TOPSIS Models[J]. Mathematical and Computer Modeling，2004（40）：721-727.

[21] Pu，H.D.，Chung，H.Y.. Inter-company Comparison Using Modified TOPSIS with Objective Weight[J]. Computers and Operations Research，2000，27（10）：963-973.

[22] 陈雷，王延章. 基于熵权系数与TOPSIS集成评价决策方法的研究[J]. 控制与决策，2003，18（04）：456-459.

[23] Chung，T.C.. Facility Location Selection Using Fuzzy TOPSIS under Group Decisions[J]. International Journal of Uncertainty，Fuzziness and Knowledge-Based Systems，2002，10（06）：687-701.

[24] Opricovic，S.，Tzeng，G.H.. Compromise Solution by MCDM Methods：A Comparative Analysis of VIKOR and TOPSIS[J]. European Journal of Operational Research，2004（156）：445- 455.

[25] 孫晓东，焦玥，胡劲松. 基于灰色关联度和理想解法的决策方法研究[J]. 中国管理科学，2005（04）：63-68.

[26] Feng，L.S.，Jeffrey，F.. A Brief Introduction to Grey Systems：Foundation，Methodologies and Application[M]. Slippery Rock，ⅡGss Academic Publisher，1998.

[27] Xiao，S.P.. Analysis and Application for Gray Correlation Theory[J]. Intelligent Engineering Systems through Artificial Neural Networks，1996（06）：149-154.

[28] 蒋红梅，魏勇. 灰色离散Verhulst直接建模模型的构建[J]. 统计与决策，2015（21）：63-65.

[29] 李晔，丁圆苹. 白化权函数已知的区间灰数Verhulst预测模型[J]. 数学的实践与认识，2020，50（20）：308-314.

（责任编辑：罗欣）

基金项目：本文系2021年度哈尔滨商业大学国家级创新创业训练计划项目“数学实验方法下地区教育改革实践效果评价与应对”（项目编号：202110240015）阶段性成果。

作者简介：王广林（2000 —），男，学士在读，哈尔滨商业大学会计学院，研究方向：会计理论与实务;张劲松（1965—），女，博士，哈尔滨商业大学会计学院院长，教授，研究方向：会计理论与实务;潘正（2001—），男，学士在读，哈尔滨商业大学会计学院，研究方向：会计理论与实务。