门架式抗滑桩设计参数优化与桩体变形分析
王鹏斌 , 阎长虹 , 万佳佳, 郭建强, 娄志会 , 郭书兰
1) 南京大学地球科学与工程学院,南京,210046;2) 北京城建中南土木工程集团有限公司,北京,102200; 3) 南京地铁集团有限公司,南京,210008
内容提要: 近年来,因门架式抗滑桩具有较高的能效比,可以更为经济地实现有效加固,因而在大型滑坡地质灾害的治理中被广泛使用。门架式抗滑桩的设计参数选取是实际工程中的难点,因此本文采用数值模拟的方法对其设计参数的选取进行了优化研究。首先,对门架式抗滑桩的加固机理进行了阐述,详细分析了桩土的耦合作用。然后,基于加固后边坡稳定性的变化以及潜在滑移面的形态演变,对桩的设计参数进行了优化分析。在此基础上考虑到门架式抗滑桩的显著特点是在联系梁作用下桩体结构的受力协调,本文重点量化分析了分级堆载情况下门架式抗滑桩体结构的受力协调性,特别是利用荷载分担比来量化分析前后排桩的受力协调性,根据其在不同设计参数下的变化规律,得出桩体最佳桩间距和桩排距范围分别是3D~5D和3D~4D(D为桩径);最后,建立了最佳桩体设计参数条件下桩顶位移与堆载之间关系的指数函数方程。这一研究将为门式抗滑桩的设计与变形控制提供理论依据。
近年来受极端强降雨天气的影响,宁镇地区发生了多起中型—大型的滑坡地质灾害,诸如南京江宁方山、牛首山、猪头山以及镇江跑马山等坡体中发生的中、大型滑坡,其滑动机理是由暂时性承压水浮托力及动水压力耦合作用引起山前缓坡发生滑动,其滑动面为上部细颗粒土与下部粗颗粒土界面,滑体的厚度多在25 m以内(阎长虹等,2019)。因为抗滑桩进行加固具有较好的效果,同时抗滑桩可以与其他防治措施灵活配合使用,所以在此类滑坡治理中被广泛应用。但对于某些规模较大的滑坡,单排抗滑桩的加固效果有限,且费用往往较高。为了有效提高桩的能效比,一种双排支护结构的异型抗滑桩——门架式抗滑桩应运而生。相比于单排大直径桩,门架式抗滑桩可以提供更大的抗力,并且具有协调变形的优点和较好的经济性(Zhao Bo et al.,2017)。
门架式抗滑桩的桩间距、桩排间距及联系梁尺寸等设计参数会直接影响其支护效果及工程成本,因此合理的设计参数对实际工程至关重要。由于门架式抗滑桩结构较为复杂,很难采用解析法进行分析。数值模拟分析方法能适用各种复杂的地质条件,同时可以考虑岩土体与结构物之间的相互作用,采用数值模拟分析方法进行参数优化具有显著的优势,因而被广泛采用(Ashour et al.,2012)。邓飚(2014)通过ANSYS有限元软件,详细分析了门架式双排桩的桩顶位移以及桩身受力情况,得到了最佳桩排距为2~4倍桩宽。Liu Xinrong等(2018)利用ABAQUS数值模拟软件通过对h型抗滑桩所受的滑坡推力和抗力分布进行分析,对其嵌固深度、桩排距等设计参数进行了优化分析。陈冲等(2019)通过建立复合结构的桩模型,分析了桩加固后边坡的稳定性变化情况和边坡潜在滑移面形态演变过程,得到圆形抗滑桩间距为3倍桩径时加固效果最好。Qiao Shifan等(2020)通过数值模拟分析比较门架式抗滑桩加固前后边坡稳定性以及桩体结构变形情况,得到矩形门架式抗滑桩最佳桩间距和桩排距分别为2倍桩横截面长度和宽度。
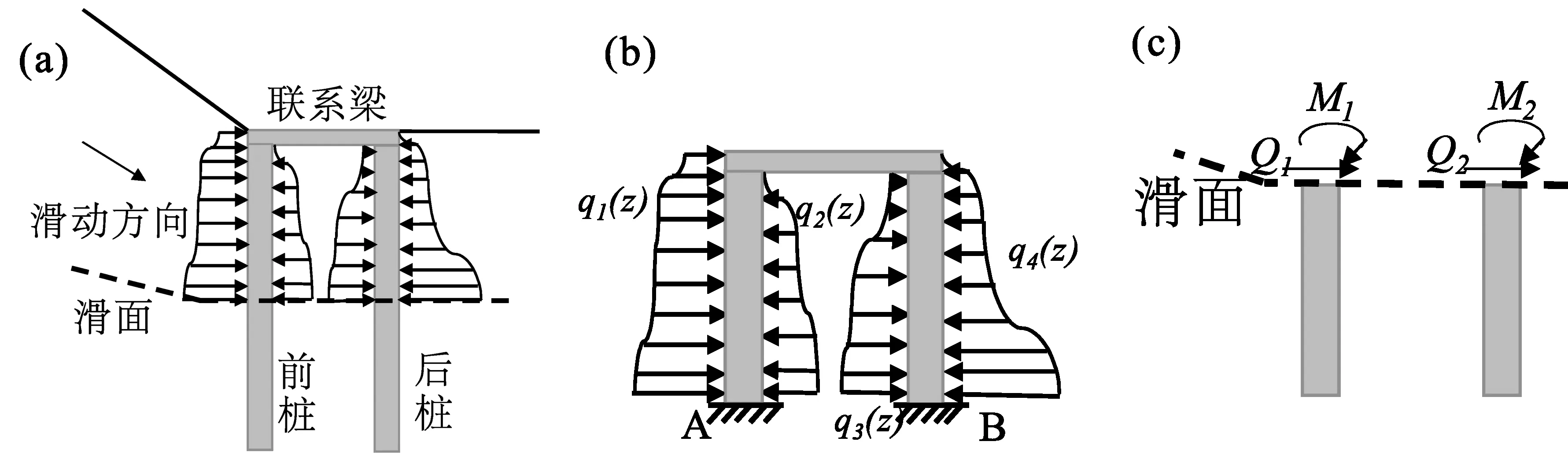
图1门架式抗滑桩受力模式图Fig. 1 Stress mode diagram of portal anti-slide pileQ—剪力; M—弯矩; q—土体作用力; z—桩埋深Q—shear force; M—bending moment; q—soil force; z—pile buried depth
但是,门架式抗滑桩的显著特点是有效利用桩土耦合作用提高其抗滑能力,其中最为关键的是联系梁作用下的桩体结构受力协调性,从已有的研究资料来看,对这类异形桩的参数优化时对这一点的研究较少。因此本文通过PLAXIS3D数值模拟软件建立了门架式抗滑桩支护的边坡模型,分析了桩加固后边坡稳定性和潜在滑移面的形态变化,并着重研究了在坡顶分级堆载作用下前后排桩的受力情况,提出了荷载分担比这一概念,来量化分析桩身受力的协调性,得出最优桩间距与桩排距。同时,探明了在最优设计参数下桩体的变形规律,为门架式抗滑桩的设计及变形监测提供科学依据。
1 加固机理分析
对于门架式抗滑桩这类双排桩的结构受力研究,很多学者基于对桩—土间的力学关系的假定与简化来进行了大量的研究,并建立了不同的计算模型(周翠英等,2005;刘鸿,2007;钱同辉等,2009;祁斌等,2011;申永江等,2014)。本文在其基础上进一步对门架式抗滑桩的加固机理进行分析,门架式抗滑桩是利用排桩联系梁结构形成桩土联合效应来共同抵抗滑坡的推力。具体来说,滑坡推力首先作用于后桩,然后通过联系梁作用于前桩,随着滑坡的进一步发展,推力也通过两桩之间的土拱效应作用于前桩,并且前桩前缘的坡体也会提供一部分抗滑力,最终后桩、前桩、联系梁和土体“四合一”共同抵抗滑坡推力。因此,在滑坡推力作用下门架式抗滑桩的受力情况如图1所示,根据其与滑面的位置关系可以分为两个部分。
滑面以上桩体结构按照其受力特征,可以按照平面刚架来分析,如图1b所示,即将滑面处的两个约束条件考虑为固定端约束,前后排桩与联系梁间的连接考虑为刚性连接。后桩受滑坡体推力q1(z)和桩间土体抗力q2(z)的共同作用,前桩受桩间土体所传递的土压力q3(z),以及桩前坡体的抗力q4(z)。采用结构力学中的力法,可得该部分的受力如图2所示。

图2采用力法分析的基本体系Fig. 2 The basic system of force analysisq—土体作用力; z—桩埋深; X—解除约束后的未知力q—soil force; z—pile buried depth; X—unknown force after the constraint is released
根据门架式抗滑桩结构位移条件可以得出如下方程:
(1)
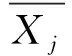
然后,将基本结构在已知力作用下的系数、自由项计算式表示如下:
δij=δji=
(2)


图 3 边坡与门架式抗滑桩模型Fig. 3 Model of slope and portal anti-slide pile
最后通过平衡条件求出该结构的内力;
(3)
(4)
其中:X1、X2、X3为解除B处约束所设置的三个未知力;MP=M(E,G,I,A,qi(z))、QP=Q(E,G,I,A,qi(z)),qi(z)为桩体所受荷载分布函数,z为桩体埋深。
滑面以下桩体部分的受力可以根据winkler弹性地基梁模型来近似求解,如图1c所示。这里根据公式(3)和(4)可以求得到滑面处桩体截面上的内力,分别为M1、Q1和M2、Q2。其滑面以下的桩体内力计算公式如下:
(5)
Qz=x0A4zβ3EI+φ0B4zβ2EI+M0C4zβ+Q0D4z
(6)
将滑面处桩截面内力代入上式计算,并联立桩底的边界条件方程,对滑面以下的桩的内力进行计算。对于均质土坡,桩底边界可以按铰支处理。其中:Mz、Qz表式滑动面下任一截面z处的弯矩和剪力;β为桩的变形系数;x0、φ0、M0、Q0为滑面处位移、转角、弯矩、剪力;Aiz,Biz,Ciz,Diz为随桩埋深变化的无量纲系数。
2 计算模型与桩土耦合作用分析
2.1 模型的建立
基于PLAXIS3D有限元分析软件建立如图3所示的三维边坡模型,模型长140 m,高45 m,坡高15 m,坡率为1∶1.33。门架式抗滑桩采用桩径D=1 m的圆桩,桩顶联系梁采用截面尺寸1 m×1 m的长方体,选用实体加密单元、线弹性材料模型。边界条件采用标准固定边界,即四周竖直边界法向固定约束,底部水平边界固定约束,上部边界自由。在坡顶施加一个宽度为4 m的分级竖向荷载(0~90 kPa,模拟到边坡稳定性系数小于1),用于模拟分级堆载工况下边坡及门架式抗滑桩的受力和变形特性。
本文选用有限元强度折减法进行计算分析。强度折减法是将黏聚力c与内摩擦角φ逐渐降低,直至土体达到极限平衡,并且得到土体临界状态时的c′和φ′,将安全系数定义为初始强度参数与临界强度参数之比(Zienkiewicz et al.,1975),其关系如式(7):
(7)
利用强度折减法分析岩土体的稳定问题,可以考虑岩土体的非线性本构关系(李翠华等,2013)。相较于极限平衡法,在分析边坡稳定性时,可以不用预先假定破坏面的形态以及位置,并且考虑土体渐进的破坏过程。
2.2 桩土耦合作用分析
在本文模型中,采用零厚度的弹塑性桩土界面来模拟桩—土相互耦合作用。模型中土单元与界面单元的连接关系(北京金土木软件技术有限公司,2010),如图4所示。界面单元有一个有限的厚度,而在有限元公式里每组节点的坐标均相等,即单元厚度为零。
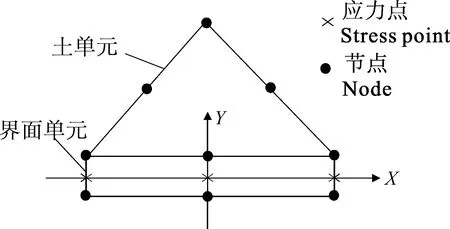
图4 界面单元上的节点和应力点分布及其与土单元的连接Fig. 4 Distribution of nodes and stress points on interface element and their connection with soil element
使用Mohr—Coulomb 准则来区分接触面内发生的微小结构变形和土体位移时的弹性变形,以及永久滑移时的塑性行为。当剪应力τ满足式(8)时桩土接触面将保持弹性
|τ|<-σntanφi+ci
(8)
当剪应力τ满足式(9)时桩土接触面将变现出塑性行为
|τ|= -σntanφi+ci
(9)
式中σn为有效正应力,φi和ci分别为接触面的摩擦角和黏聚力。桩—土相互作用的接触界面的强度与土层的强度属性有关,通过给界面选取合适的接触面折减系数(Rinter) 的值来表示,接触界面的强度属性计算规则如下式(刘志祥等,2014) :
(10)
此外,折减系数Rinter不仅折减界面强度,还折减界面的刚度。考虑桩—土接触面性质,本次模拟中Rinter值取0.65。门架式抗滑桩与土体的物理力学参数取值如表1所示。
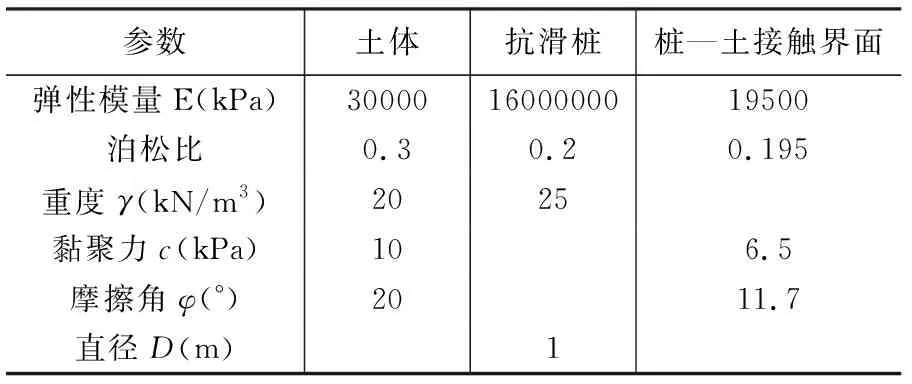
表 1门架式抗滑桩与土体参数Table 1 Parameters of portal anti-slide pile and soil
3 参数优化分析
3.1 桩间距优化分析
桩间距的优化分析,首先确定抗滑桩最佳布桩位置。前人研究发现,抗滑桩布置在边坡中部附近对边坡的加固效果最佳(朱泳等,2017)。因此笔者等将其布置在边坡中部,经过模拟试算(模拟计算边坡滑动面埋深,确定抗滑桩桩长穿过滑动面以下的部分占比为1/3~2/5)选取桩长H=15 m,对桩间距S=D,2D,3D,4D,5D,6D,7D…(D为桩径)等不同工况进行模拟分析。
不同桩间距下边坡稳定性系数变化如图5所示,随着桩间距的增大,边坡稳定性系数不断减小。桩间距从D增至5D时,稳定性系数缓慢下降;而当桩间距大于5D后,边坡稳定性系数急剧下降。

图 5不同桩间距下边坡稳定性系数Fig. 5 Slope stability coefficient under different pile spacing
不同桩间距条件下的相邻门架式抗滑桩中间坡体剖面的潜在滑面形态如图6所示,当桩间距S在D~5D时,边坡的潜在滑移面被分割为上、下两个部分,没有形成贯通的滑动面,此时抗滑桩的加固效果明显;当桩间距为6D~7D时,潜在滑移面靠近坡体表面的区域被分为两个部分,但在深部区域形成了贯通的区域,此时抗滑桩的加固效果减弱;当桩间距为8D~10D时,潜在滑移面从坡顶至坡脚贯通,此时抗滑桩对边坡中间部分土体加固作用几乎消失。因此,从桩加固边坡的效果来说最佳桩间距不应超过5D。

图 6不同桩间距下桩间土潜在滑移面Fig. 6 Potential slip surface of soil between piles under different pile spacingS—桩间距; D—桩径S—pile spacing, D—pile diameter
门架式抗滑桩常用于推力较大的边坡治理工程,因此对其设计参数的优化考虑桩身受力状态尤为重要。在一定桩间距的条件下,桩间距适当增大会使前后排桩形成的土拱更加协调,前后排桩受力也会更加均匀(邱志华,2018)。如图7所示,为不同桩间距下前后排桩最大弯矩的变化情况。在各级坡顶堆载下,随着桩间距的增大,前后排桩所受的最大弯矩值均不断增大,前排桩所受弯矩小于后排桩。桩间距为D~4D与6D~7D时,桩身最大弯矩提升明显,这是由于桩间距增大导致单个桩加固区间增大而引起的。在桩间距为4D~6D与7D~9D时,桩身最大弯矩提升缓慢,前者是由于土拱效应的存在,桩间土拱分担了加固区间增大引起的推力增加,后者则是当桩间距大于6D后,桩间距开始大于单个桩加固范围,土拱效应消失所导致的。
此外,从图7还可以发现,在一定桩间距下,随着坡顶堆载增大,前后排桩的最大弯矩越来越接近,这说明在大推力边坡治理工程中门架式抗滑桩可以充分发挥前后排桩的加固作用。根据门架式抗滑桩的机理可知,在坡体推力作用下,联系梁可以起到协调前后排桩受力的作用,使前后排桩的受力更加均匀。为了探究联系梁对前后排桩的协调作用,本文提出了荷载分担比(R)这一概念,其定义如式(11)
(11)
其中Mf和Mr分别为前桩弯矩和后桩弯矩。该参数可以明确反映前后排桩受力的差别,也量化了门式桩前后排桩的受力协调性,荷载分担比(<1)越大表明前后排桩的受力越协调,桩体材料的利用也越充分。
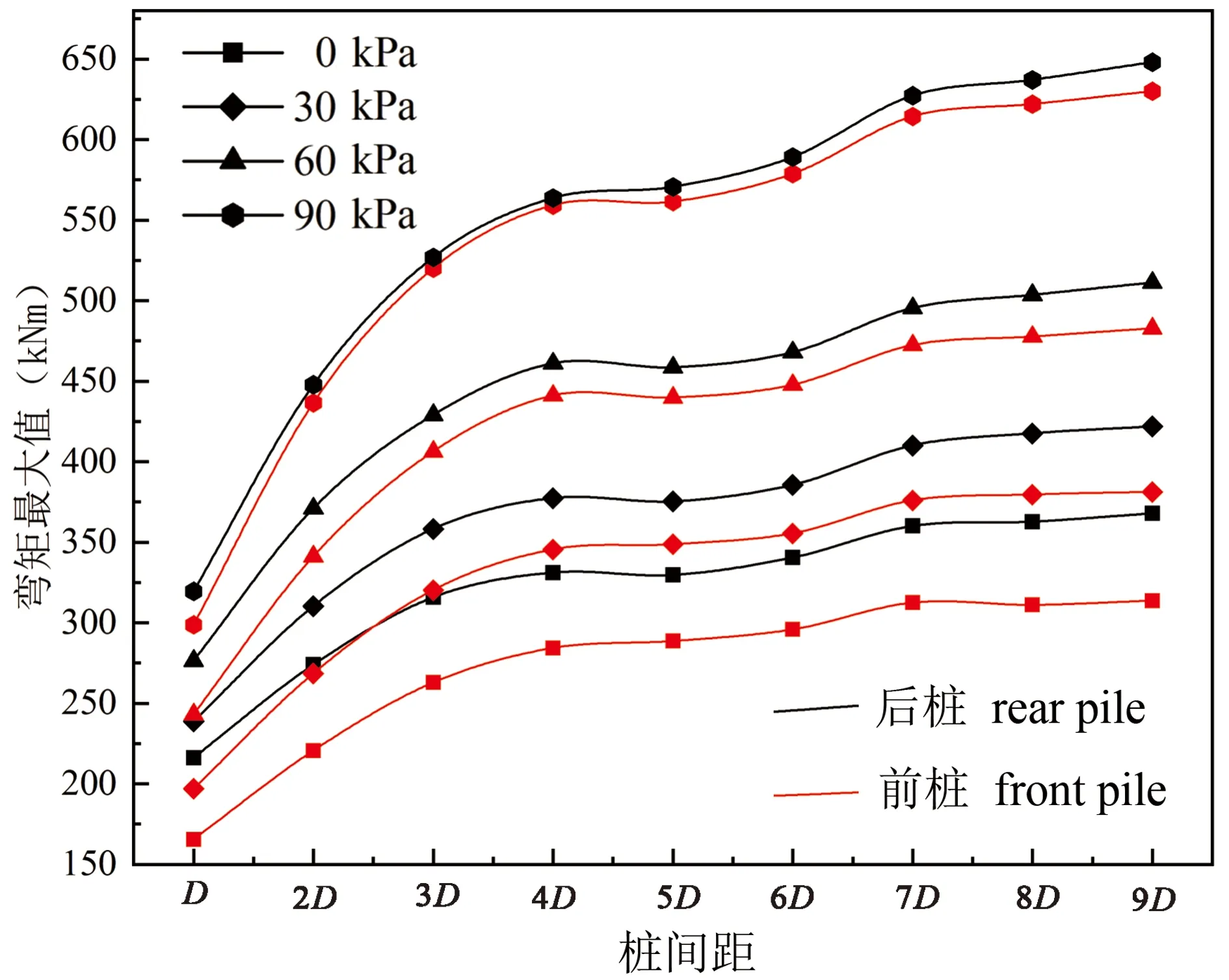
图7 不同桩间距下前后排桩最大弯矩值Fig. 7 Maximum bending moment of front and rear row piles under different pile spacing
由图8可知,在各级坡顶堆载作用下,荷载分担比最低值为0.765,最高值达到了0.989,这表明门架式抗滑桩的受力协调性较好。在桩间距一定时,随着坡顶堆载增大,荷载分担比也逐渐增大。这表明随着坡顶堆载增大,前后排桩受力逐渐接近,体现出了门架式抗滑桩在大推力滑坡治理工程中相较于传统抗滑桩的优势。在坡顶堆载一定时,随着桩间距增大,荷载分担比呈现先增大后缓慢减小的变化规律。在坡顶堆载小于60 kPa时,前后桩的荷载分担比在桩间距等于5D时取得最大值;在坡顶堆载大于60 kPa时,荷载分担比在桩间距等于4D时取得最大值,并且在桩间距等于3D~5D这一区间,荷载分担比维持较高水平。因此,从前后排桩受力协调这个角度来分析,门架式抗滑桩的最佳桩间距在3D~5D。
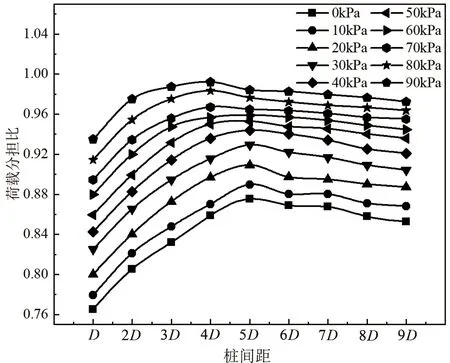
图 8不同桩间距下前后桩荷载分担比Fig. 8 Load distribution ratio of front and rear piles under different pile spacing
综上,从门架式抗滑桩对边坡的加固效果和桩体受力协调性这两个方面分析,可以得出门架式抗滑桩的最佳桩间距为3D~5D。
3.2 桩排距优化分析
桩排距的优化分析,首先将桩布设在坡体中间位置处,选取桩长为15 m,依据上文结论选取桩间距S=3D。模拟研究桩排距T=2D,3D,4D,5D,6D,7D,8D,9D…等不同工况。
不同桩排距下边坡稳定性系数的变化情况如图9所示。由图9可以看出,随着桩排距增大,边坡稳定性系数不断增大,抗滑桩的加固效果也越好。桩排距从2D增至5D时,边坡的稳定性系数提升明显,而当桩排距大于5D后,曲线呈缓慢递增。
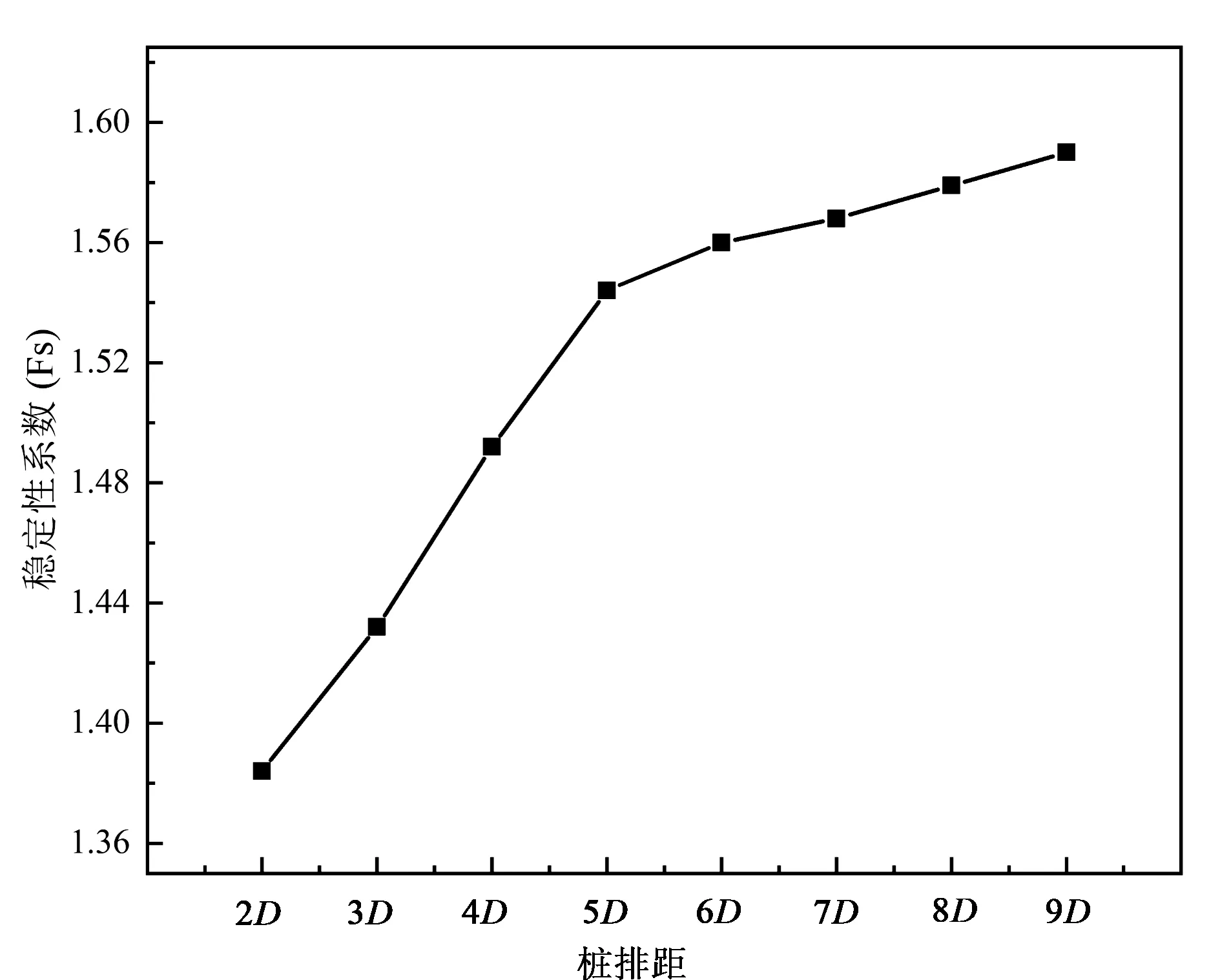
图9 不同桩排距下边坡稳定性系数变化Fig. 9 Variation of stability coefficient under different pile row spacing
不同桩排距下边坡的潜在滑移面形态如图10所示,各个排距下桩间坡体滑移面形态整体类似,均被分为上下两个独立的部分。当桩排距在2D~4D时,潜在滑移面被分为上下独立的区域,此时抗滑桩的对边坡的加固效果明显。当桩排距大于5D时,上下两部分潜在滑移面间的剪应力极小的中间区域即前后桩之间被加固的土体逐渐增大,并且随着桩排距的增大,前后排桩的加固区域越来越大,加固效果也越来越明显。此外,随着桩排距的增大,在联系梁的顶部附近的坡体出现了剪应力集中区域。在桩排距为8D时形成了从坡顶至联系梁顶部贯通滑移面,这可能会导致桩体加固区域上方出现局部变形破坏。当桩排距大于等于7D后,边坡则出现了绕过桩底的深层滑动带。这两个变化趋势表明采用过大的桩排距门架式抗滑张加固边坡,可能出现局部滑坡破坏以及深层滑动破坏。
同时计算分析了不同桩排距下前后排桩最大弯矩的变化情况,如图11所示。由图可知在各级坡顶堆载下随着桩排距的增大,前后排桩的最大弯矩也是在不断增大,增长速度逐渐减慢,这是由于桩排距的使整个桩体的加固范围增大,进而导致桩体受力增加,增长速度减慢则是由于坡体潜在滑移区域有限,增加排距导致加固范围增大也是有限度的。此外,在桩排距一定时,随着坡顶堆载增加,前后排桩的最大弯矩差值逐渐减小,受力逐渐接近。
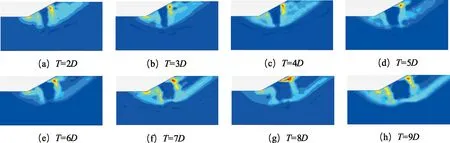
图10不同桩排距下桩间土潜在滑移面形态Fig. 10 Potential slip surface morphology of soil between piles under different pile row spacingT—桩排距; D—桩径T—pile row spacing; D—pile diameter
对于上述前后排桩受力的变化,其根本原因是桩排距的变化导致了联系梁的尺寸发生变化,这会直接影响联系梁对于前后排桩受力的协调作用。因此对于桩排间距的优化分析将着重考虑桩的荷载分担比的变化。由图12可知,在任意桩排距下,随着坡顶堆载的不断增大,桩体荷载分担比也在不断增大,这进一步证明了门架式抗滑桩在治理大推力滑坡的优势。随着桩排距的不断增大,荷载分担比先增大后减小,存在荷载分担比极值。在坡顶堆载小于60 kPa时,前后排桩的荷载分担比在桩排距等于3D时取得最大值,当坡顶堆载大于等于60 kPa时,荷载分担比在桩排距等于4D时取得最大值。这表明从荷载分担比的角度分析,门架式抗滑桩存在一个最优桩排距。在最优桩排距条件下,联系梁可以充分发挥对前后排桩受力的协调作用,提高桩体材料的利用率,同时这个最优桩排距还与边坡顶部堆载大小也有关。在坡顶堆载小于60 kPa和大于等于60 kPa时,最佳桩排距分别为3D和4D。
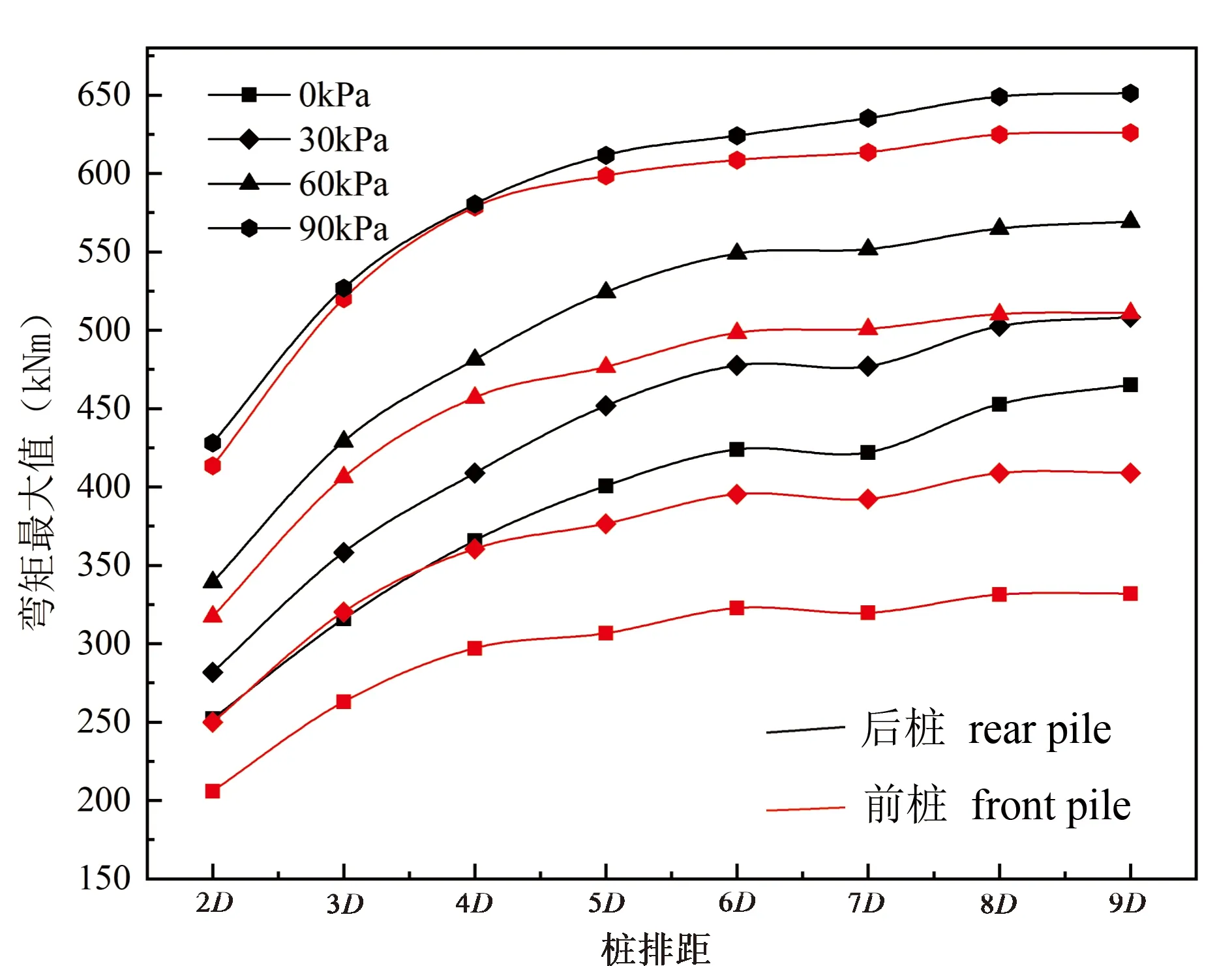
图11 不同桩排距下前后排桩最大弯矩值Fig. 11 Maximum bending moment of front and rear piles under different pile row spacing
因此,通过边坡稳定性系数的变化、潜在滑移面的变化以及桩体受力协调性的变化可以得出最佳桩排距为3D~4D。这一桩排距区间,既保证了桩加固边坡的效果,也使得门架式抗滑桩的优势得到充分发挥。

图12 不同桩排距下门前后排桩荷载分担比Fig. 12 Load distribution ratio of front and back row piles under different pile row spacing
4 分级堆载下桩体变形分析
抗滑桩施工完成后,后期监测抗滑桩的加固效果是必不可少的工作。通常抗滑桩在加固边坡时,可以从桩顶位移量来判断抗滑桩的加固效果,桩顶位移越小,其加固效果越好(欧孝夺等,2012)。因此根据前文的参数优化所得结论,桩间距与桩排距均选为3D,桩布置在坡体中部,前后桩桩长取20m,坡顶施加0~90 kPa的分级堆载来研究前后排桩的变形特性。门架式抗滑桩的桩身位移情况如图13(图中以由近山侧指向远山侧为正值)所示,前后排桩的桩身位移由下至上不断增大,并且随着坡顶堆载的增大,桩身位移也在不断增大。前后排桩由于联系梁的刚性连接,其桩顶位移最大且相等,下部桩身位移大小也是相近的,这也反映在联系梁(其桩梁变形控制在一定变形量范围内)的作用下,前后排桩变形更加协调,能充分发挥前后排桩的抗变形能力。在分级坡顶堆载作用下,相同深度处的桩身位移增长幅度是非线性的,其增长幅度随着堆载增加而不断增加的。
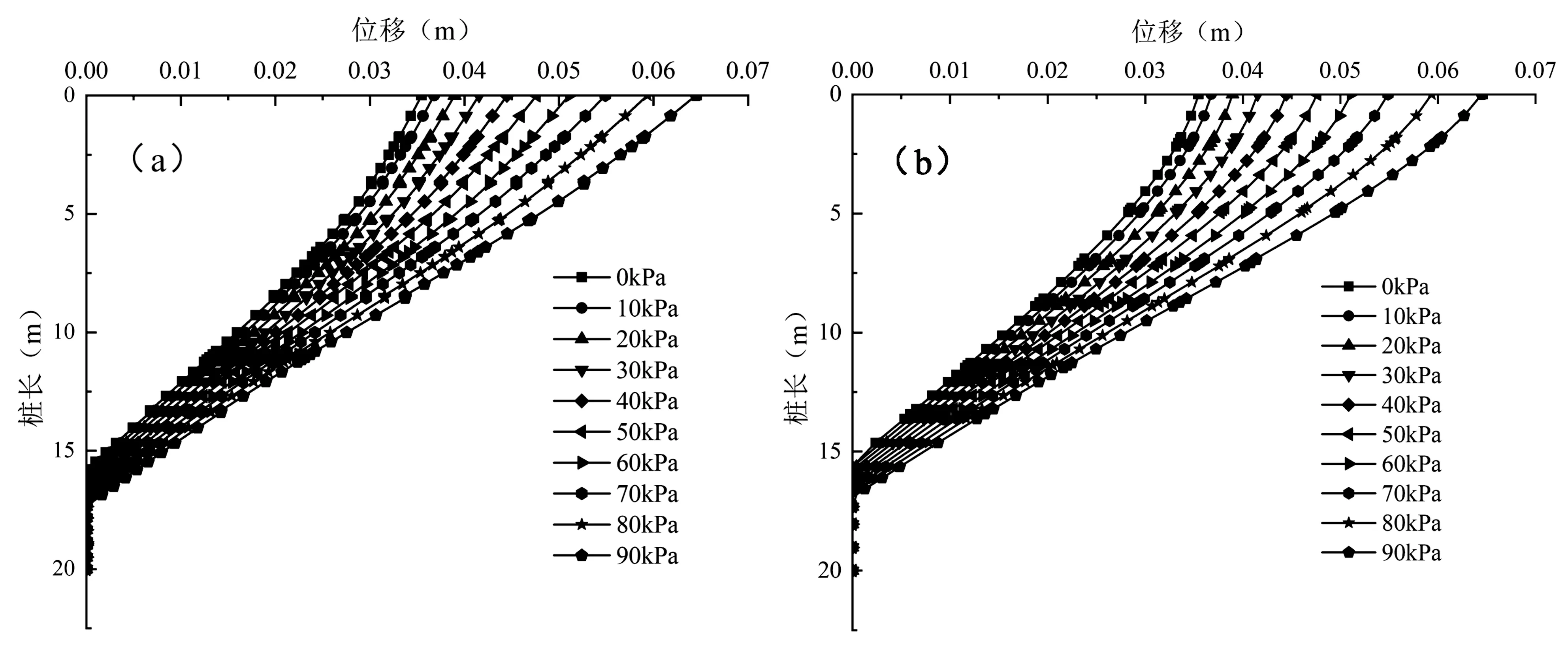
图 13 分级堆载作用下桩身位移:(a)前桩;(b)后桩Fig. 13 Pile displacement under graded load:(a)the front pile;(b)the rear pile
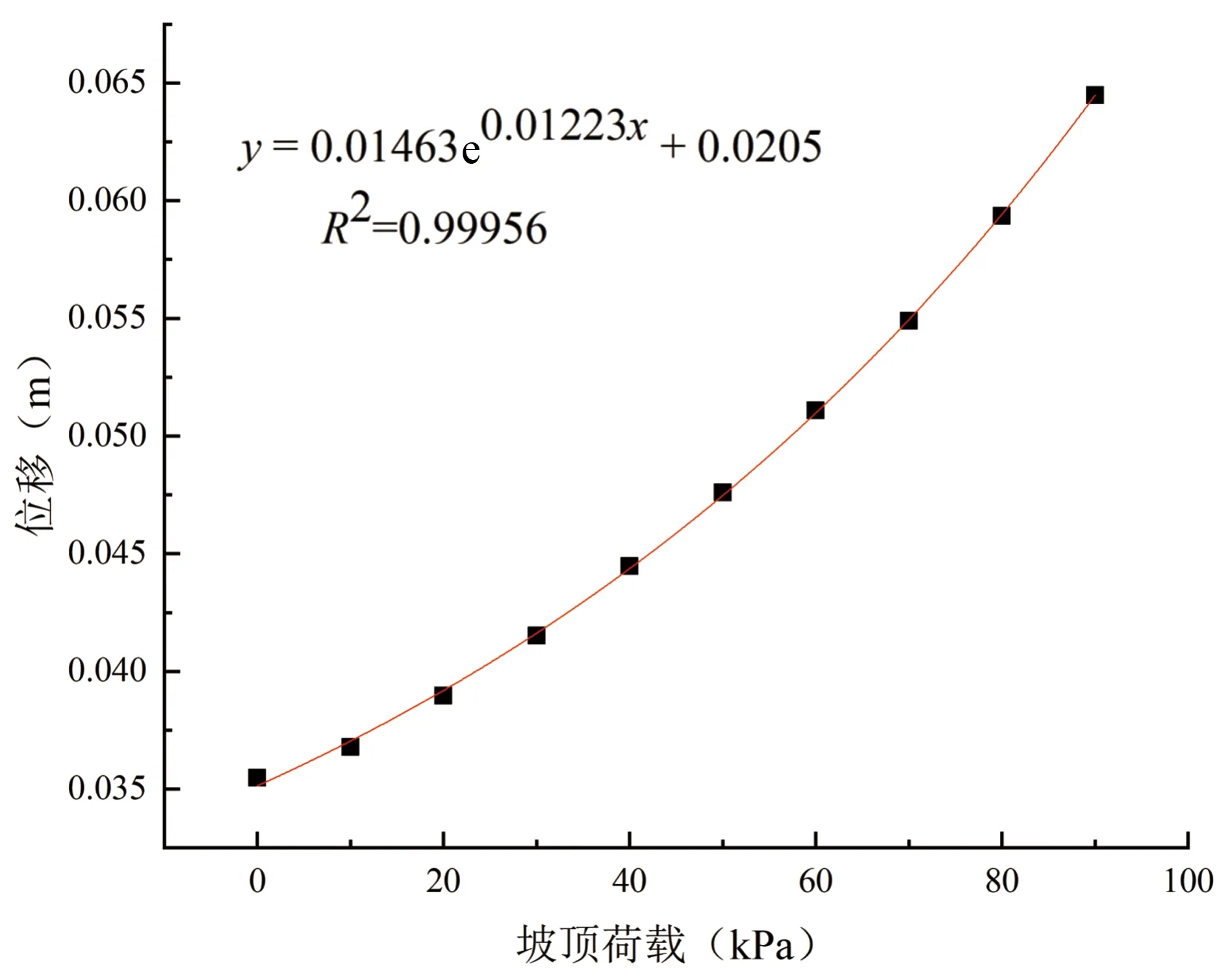
图14分级堆载作用下桩顶位移曲线Fig. 14 Displacement curve of pile top under graded load
选取抗滑桩的桩顶水平位移进行研究,如图14所示,对桩顶位移与分级堆载关系曲线进行拟合,该曲线服从如下指数函数:
y=Ae(-x/t)+y0
(12)
式中,A为一个反映抗滑桩力学特性的综合指标;t为一个拟合参数,其受坡顶堆载大小以及分布的影响,y0为与桩顶初始水平位移有关的量。根据该式可对抗滑桩变形进行预测,并在抗滑桩现场监测过程中得到修正,同时还可通过预测模型对桩身变形进行控制。
5 结论
本文通过数值模拟方法,分析优化了门架式抗滑桩的桩间距、桩排距等设计参数,并研究了坡顶分级堆载条件下桩体的变形特性,得出了以下结论:
(1)门架式抗滑桩区别于普通双排桩的关键是存在连接前后排桩的联系梁,在桩体加固边坡的过程中,联系梁起到了协调前后排桩受力的作用,荷载分担比这一参数可以很好地量化联系梁协调作用。
(2)桩间距对桩体加固边坡的效果影响显著。综合考虑边坡稳定性系数、潜在滑移面形态以及桩体受力协调性可以得出,门架式抗滑桩的最佳桩间距为3D~5D。
(3)桩排距越大,抗滑桩加固边坡的效果越明显。前后桩荷载分担比随桩排距的增加先增大后减小,存在荷载分担比峰值,最佳桩排距为3D~4D。
(4)桩顶水平位移在坡顶分级堆载不断增大的条件下呈现指数函数形式发展,根据本文中所得到的拟合公式可以对门架式抗滑桩变形进行预测,从而在实际工程中准确地监测抗滑桩支护情况。

