Stacking算法在小样本预测上的适用性研究：以实验室金属挂片的腐蚀速率预测为例

郑鹏飞，杨洋，石鑫，闻小虎

（1.西南石油大学地球科学与技术学院，四川成都，610500；2.中国石油化工集团公司碳酸盐岩缝洞型油藏提高采收率重点实验室，新疆乌鲁木齐，830011；3.中国石油化工股份有限公司西北油田分公司工程技术研究院，新疆乌鲁木齐，830011）

1 简介

在石油和天然气行业中，油气管道因其经济性和安全性，成为了目前最主要的油气输送方式之一，而碳钢材料是使用较广泛的材料之一。因油气管道中存在CO2以及H2S等气体，所以在油气管道内会形成酸性的环境，随着投产年限的增加，这种腐蚀环境对碳钢管道的腐蚀作用会逐渐累积。为了更好的研究油气管道腐蚀，目前有大量的学者通过建立传统物理模型、使用人工智能等方法建立了多种腐蚀预测模型，但由于管道检测数据的数量及维度并不总是能满足模型的要求，以及各模型的适用性的限制，这些模型并不能广泛的应用于实际的生产，所以利用实验室条件，深入研究金属腐蚀则显得尤为重要。

我们首先利用动态反应装置获取了99条实验室条件下的金属腐蚀数据，然后使用PCA降维、箱线图去离散值、标准化等预处理步骤之后，选择了bagging[1]和boosting[2]集成方式中的共计11种模型，并在通过10折交叉验证的方法获得最佳超参数后，将其组合的方式，对各种组合的预测性能进行对比和研究。我们的实验发现在本实验的数据集上，stacking的预测表现并不是很好，甚至大多数情况不如基础的集成学习算法；性能最好的基础模型的组合数量为5个；当Extratrees模型参与stacking集成时，更容易提高预测性能。

2 实验数据

该实验数据的获取方法为：以四个L360N金属挂片（50×10×3mm）为一组，置入动态反应装置内，通过人为控制压力、温度、CO2分压等参数，设置实验周期为7天，通过称量金属挂片在反应前后的质量差，并与反应时间相除的方式，就可以得到每组实验环境条件下的平均腐蚀速率。本实验共采集到99组数据，其中原始参数包括液体流速，温度，倾角，CO2分压，H2S分压，然后使用多相流模拟软件：OLGA，对流型，流量，剪切应力等在内的其他18个维度的参数进行了扩充，以探究更多因素对腐蚀速率的影响。

表1 实验数据参数表

3 实验方法

集成学习是一种优雅的数据挖掘技术，它利用将多种算法组合起来的策略，以达到提高整体预测性能的目的，而根据集成方式，又可以将集成学习分为基于集中不同学习算法的分类和基于一种算法的分类。在基于同一种算法的分类模式中，bagging和boosting是该模式的两种代表算法，bagging采用并行结构进行集成，而boosting采用线性结构进行集成。

本实验首先进行数据的预处理：对收集到的99条实验室金属挂片腐蚀数据，基于标签值，利用箱线图对整体数据进行离散值剔除处理，然后设置随机种子（222,444,666）用来打乱顺序（随机种子是随机取的，即使它们看起来有规律，但是能很好的实现乱序处理），可以获得三组排序不同的数据集。对数据以9:1的比例分割为训练集和测试集，在进行标准化处理后，以PCA分析中保留90%为标准，选择数据的维度。为了对stacking的预测效果进行验证，本研究以10倍交叉验证与网格搜索相结合的方式，找到了每个集成模型的最佳预测超参数，该步骤的目的主要是通过设置相同超参数，从而减小超参数对各个模型预测的影响。当集成模型的参数设置完成以后，利用循环遍历的方式，将所有模型的组合方式分别利用stacking的组合模式进行预测误差计算，然后将该结果与各个基础的集成模型进行对比，就能分析出stacking模式是否适用于该数据集，以及哪种组合在stacking模式下有最好的预测效果。

4 实验结果

4.1 集成模型预测性能对比

当数据集的分割情况不同时，对模型的预测影响较大，比如当随机分割因子取666时，其预测误差明显高于其他两组，而从整体来看各集成模型之间并无明显差异。为了更加科学的对各个模型的预测误差进行排序，本研究采用了Friedman排序的思想，首先对不同分割情况下的预测结果进行排序，再基于排序结果求均值的方式，确立最终的模型排序，其结果显示，Bagging+KNN、Extra trees、Bagging +CART的集成方式分别占前三的排名。总体来说，使用bagging的方式进行集成，在该数据集上具有最小的预测误差。当随机因子为222和444时，预测误差最小的模型为bagging+KNN，MSE误差值为0.000909；当随机因子为666时，预测误差最小的模型为bagging+CART模型，其MSE误差值为0.000934。

4.2 Stacking组合模型预测误差结果

Stacking集成方式不限制子模型的数量以及类别，所以当有11个集成模型被用来进行组合时，其能够建立非常多的组合方式，本实验为了控制组合的数量，每一种模型在一次组合中只被使用一次。为了简化模型展示效果，本研究采用散点图的方式，对不同组合数量的预测误差进行了分区展示，如Figure 1所示。从该图中能够看出，随着组合数量的增加，其预测的误差值变得更加集中，而几乎在每一个分段区间内都有一部分相似的误差变化规律。Table2展示了不同集成模型参与组合后提升预测性能的比例，该结果表明当随机分割因子为222和444，且组合数量为5个时，均存在预测误差最小的组合，其中随机分割因子为222时，最佳组 合 方 式 为 ：Random Forest、Extra trees、LightGBM、Bagging+SVR、Bagging+CART；随机分割因子为444时，最佳组合方式为：Extra trees、Bagging+KNN、Bagging+SVR、Bagging+CART、Adaboosting+CART。而在这些模型中，Adaboosting+SVR、Extra trees、LightGBM参与 stacking组合后，提升模型预测性能的能力更强。即使stacking中存在预测效果变好的组合情况，但无论从单个集成模型的预测性能，还是预测性能提升的占比来看，Stacking集成模式，都不是很适用于该数据下的小样本预测。

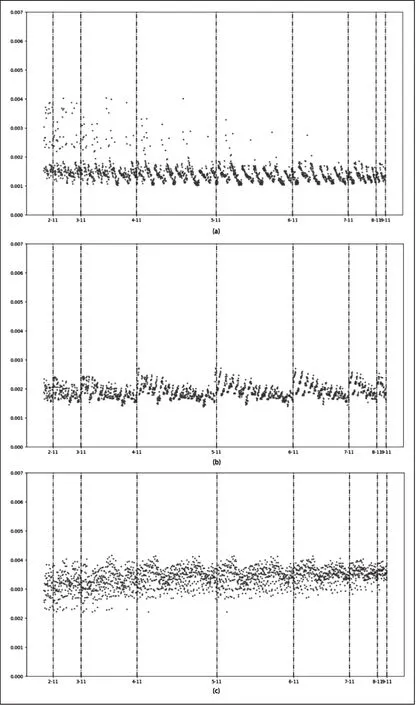
图1 Stacking模式各组合方式预测误差图（横坐标表示基础集成模型的类型）

表2 不同集成模型参与stacking组合后提升整体性能的对比表

Adaboosting+SVR 211/312 150/288 0/18 Adaboosting+CART 162/312 160/288 0/18总计 312/2024 288/2024 18/2024

5 讨论

在本研究中，虽然以箱线图的方式进行了离散值的剔除，但是该方式只以腐蚀速率列为基准，而没有考虑其他维度的数据项，之所以采取这种剔除方式，是因为在人工智能的预测场景下，数据的数量会很大程度影响到预测的精度，如果过多的剔除数据，会导致整体的预测性能下降。在该实验中，当随机因子为666时，预测的整体精度出现了明显的下降，这也是因为该实验中，并未完全剔除离散值，而当离散值被随机分配到测试集中时，模型的预测值无法在离散数据上进行很好的泛化。

Stacking集成方式虽然在某些组合的情况下会提升预测性能，但是仍然有很多的组合方式的预测能力减弱了，比如当子模型本就是一个预测性能非常好的模型时，如果搭配其他类型的模型进行组合，其组合后的预测性能也不能超越这个子模型。而且无论是哪一种组合方式，以及无论是哪一种分割情况，几乎所有的stacking组合模式的预测性能都没有超越单个集成模型中的最好的那一个预测效果，虽然在分割因子为444时，存在个别组合方式略好于单个模型的预测精度，这主要是因为在单个模型的预测性能中，并未有预测性能极好的模型出现。所以在小样本的条件下，如果选择的基础模型的预测性能已经极好了，那么没有必要再考虑使用stacking方式将其与其他基模型进行集成，因为这很大程度上并不能增加模型的预测性能，反之，如果在基模型上的预测性能是中等的，那么尝试使用stacking模式进行集成，将有可能提升模型的预测精度，这与其他学者[3]的研究基本一致。而通过Table2 的结果能够看出，当基础集成模型的数量为5个时，出现预测效果最好的组合的概率是最大的，而在本次实验中，Adaboosting+SVR、Extra trees、LightGBM参与的组合，其预测性能提升的概率更大，其中Adaboosting+SVR与LightGBM单独预测的表现就不是很好，但是这些模型更容易在其他更好的模型参与下进行优化，而Extratrees模型其本身的预测性能就较好，在其参与组合后还有很大的概率增加其预测性能，所有当考虑使用stacking模型进行集成时，Extratrees模型是一个较为理想的基础模型。

6 结论

根据本实验所获得的结果，能够得到以下结论：（1）Stacking算法并不适用于解决当前数据集条件下的小样本预测问题；（2）当小样本数据集中存在离散值时，Bagging算法的预测误差小于Boosting算法；（3）在小样本条件下，当以每种基础模型只参与一次集成的原则进行stacking集成时，如果其中一种基础模型的预测效果明显好于其他的，那么其集成后的预测结果很有可能都不会好于仅单独使用该基础模型预测的结果；而当各基础模型的预测性能相近，且其预测表现不是很糟时，采用stacking方式进行集成，可能存在提升预测效果的组合，但是比例并不是很多；（4）在小样本条件下，并不是集成模型的数量越多，stacking组合他们之后的预测效果就越好，而是随着集成模型增多，各种组合的预测结果的波动范围越小，这是平均化后导致的结果；（5）在本实验的数据条件下，当集成模型为5个的方式，进行stacking集成，获得预测效果更好的组合的概率更大。（6）extratress模型在本实验的数据条件下，不仅单独预测的性能较好，而且与其他模型进行组合时，最终提升了预测效果的比例也较大，所以应该考虑更多的使用该模型参与stacking的组合。

下一步的研究可以尝试的方向：使用其他的小样本数据集验证本实验；使用足够样本数量的数据集验证本实验；增加更多的基础模型，寻找基础模型并不是最优超参数时，对stacking集成结果的影响。